Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

4) из точки /' радиусом У—L описать

полуокружность, которая пересечет А'В'

в точках М и N; эти точки делят отрезок

А'—Г и равный ему отрезок /'—В' в отно-

шении 3:7;

5) через точки М и N провести прямые,

параллельные боковым сторонам паралле-

лограмма, и отметить точки Е', F', О' и Н',

расположенные на диагоналях;

6) построить касательные к эллипсу в

найденных точках. Две касательные па-

раллельны диагонали А'С', две другие па-

раллельны B'D'.

Получив восемь точек и столько же ка-

сательных, можно с достаточной точностью

вычертить эллипс.

В том частном случае, когда параллель-

ной проекцией квадрата, описанного около

окружности, является ромб, оси эллипса

совместятся с диагоналями ромба. В об-

щем же случае построение осей эллипса,

вписанного в параллелограмм, связано с

определением главных направлений двух

совмещенных плоских полей, находящихся

в перспективно-аффинном соответствии.

Покажем, что для любого аффинного

преобразования плоскости существуют та-

кие два взаимно перпендикулярные так

называемые г л а в н ы;е направле-

ния, которые переходят снова во вваимно

перпендикулярные.

Пусть даны ось родства 0\0

и род-

ственные точки С и С' (рис. 316). Требует-

ся провести через точку С' две взаимно

перпендикулярные прямые так, чтобы и

родственные им прямые были ортогональ-

ны. Другими словами, нужно построить

четырехугольник CMCN, углы при точ-

ках С' и С которого должны быть прямы-

ми, а вершины М и N должны принадле-

жать прямой 0|0г.

Известно, что около четырехугольника,

сумма противоположных углов которого

равна 180 можно описать окружность.

Прямые углы при вершинах С' и С долж-

ны опираться на общий диаметр MN. Зна-

чит, центр описанной окружности находит-

ся на оси родства.

Положение этого центра О определяет-

ся пересечением оси родства и перпенди-

куляра РО, восставленного к отрезку С'С

в его середине. Далее, проведя окруж-

ность радиусом ОС, находим точки М и N,

в которых она пересекает ось родства.

Соединяя М и N с С', получим искомые

прямые. Действительно, прямые МС' и

NC' перпендикулярны, так как угол, обра-

зованный ими, опирается на диаметр. По

той же причине перпендикулярны' и пря-

мые МС и NC.

Если точка С является центром окруж-

ности т, то двум диаметрам АВ и EF этой

окружности можно поставить в соответст-

вие два взаимно перпендикулярных диа-

метра А'В' и E'F' эллипса т'.

Такие диаметры эллипса называются

его осями. Построение осей А 'В' и E'F'

эллипса дано на том же рис. 316. Теперь

рассмотрим определение осей эллипса, ко-

торый нужно вписать в данный паралле-

лограмм Q'R'S'T' (рис. 317).

Прежде всего построим квадрат QRST,

родственный заданному параллелограмму.

Для упрощения чертежа ось родства

0\0

совмещаем со стороной ST. Прове-

дя диагонали в параллелограмме и квад-

рате, находим родственные друг другу точ-

ки С и С'. Остается построить окружность,

140

проходящую через эти точки и имеющую

центр на оси родства 0\0

, т. е. дальней-

шие графические построения по существу

ничем не отличаются от построений, свя-

занных с определением главных направле-

ний.

§ 66. ПОСТРОЕНИЕ

АКСОНОМЕТРИЧЕСКИХ ИЗОБРАЖЕНИЙ

» Переход от ортогональных проекций

предмета к аксонометрическому изобра-

жению рекомендуется осуществлять в та-

кой последовательности:

1. На ортогональном чертеже размеча-

ют оси прямоугольной системы координат,

к которой и относят данный предмет. Оси

ориентируют так, чтобы они допускали

удобное измерение координат точек пред-

мета. Например, при построении аксоно-

метрии тела вращения одну из координат-

ных осей бывает целесообразно совмес-

тить с осью тела.

2. Строят аксонометрические оси с та-

ким расчетом, чтобы обеспечить наилуч-

шую наглядность изображения и види-

мость тех или иных точек предмета.

Практика построения аксонометриче-

ских проекций показывает, что лучшие по

наглядности изображения получаются в

косоугольной триметрии с соотношением

коэффициентов искажения u:v:w =

= 0,9:0,5:1,0. При сравнительно неболь-

шой ширине предмета коэффициент иска-

жения по оси у необходимо увеличивать.

Хорошие результаты по наглядности да-

ет также прямоугольная диметрия с со-

отношением коэффициентов искажения

1:0,5:1.

Из косоугольных аксонометрических

проекций широко применяются фронталь-

ная диметрия (П'ЦПг) и горизонтальная

изометрия

(П'||

Hi) вследствие простоты

их построения. Как отмечалось выше,

фронтальные проекции не искажают фор-

мы фасада, а горизонтальная изометрия

сохраняет без изменения все контуры

плана.

3. По одной из ортогональных проекций

предмета чертят вторичную проекцию.

На какой координатной плоскости целе-

сообразно строить вторичную проекцию?

Решать этот вопрос следует, исходя только

из сравнительной простоты графических

построений. Вычерчивать рекомендуется

ту вторичную проекцию предмета, которая

проще других.

Если же на аксонометрическом чертеже

предстоит показать тени, то вторичную

проекцию обычно строят на горизонталь-

ной плоскости.

4. Создают аксонометрическое изобра-

жение.

Масштабы ортогонального и аксономет-

рического чертежа могут быть различны-

ми. Так, при построении прямоугольной

диметрии детали {u:v:w= 1:0,5:1) все

линейные размеры ее вдоль осей х' и z'

могут быть увеличены или уменьшены в п

раз, но тогда размеры в направлении оси

у должны быть соответственно увеличены

или уменьшены в 0,5 п.

Итак, процесс вычерчивания аксономет-

рического изображения предмета рекомен-

дуется начинать со вторичной проекции,

т. е. с построения аксонометрии плоской

фигуры, являющейся видом данного пред-

мета сверху или спереди. Поэтому прежде

всего рассмотрим примеры построения ак-

сонометрии фигур, расположенных в плос-

костях проекций.

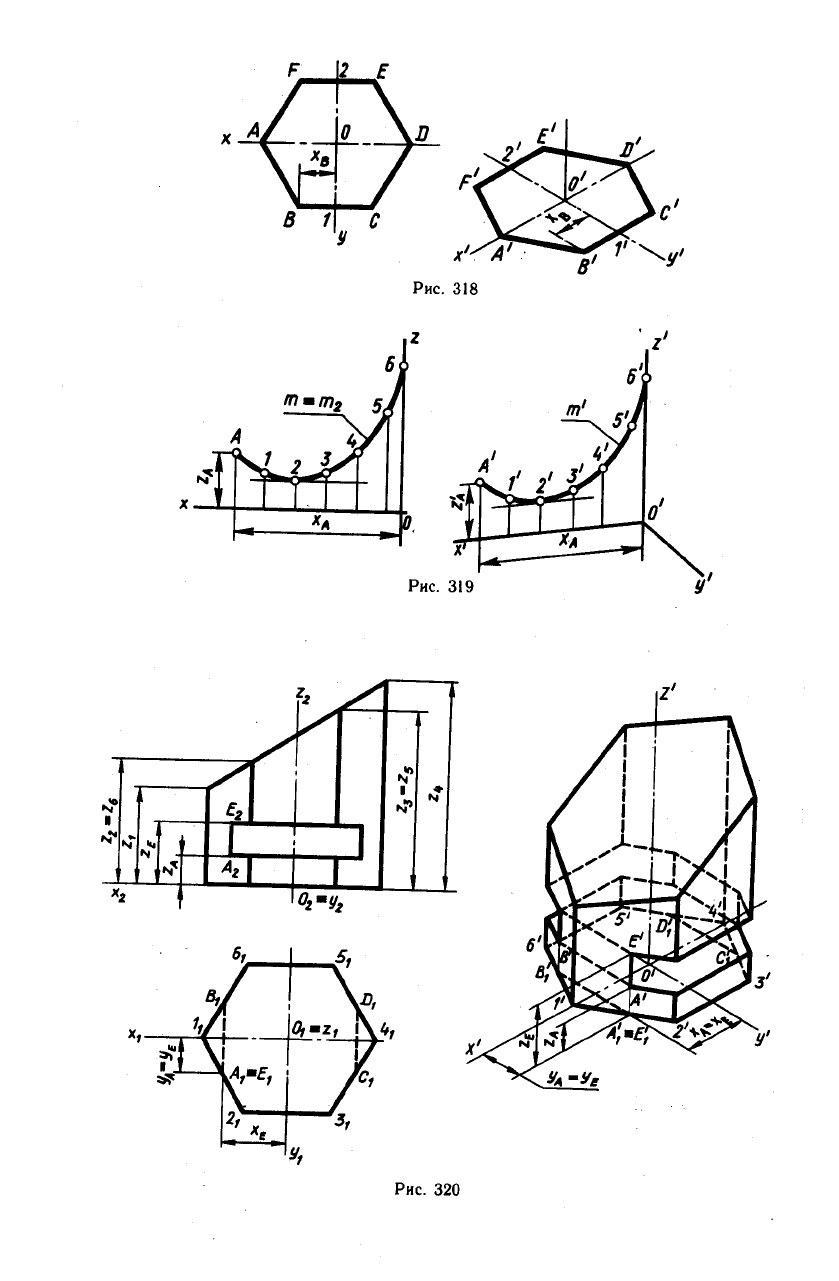
Пример 1. Построить прямоугольную

изометрическую проекцию правильного

шестиугольника ABCDEF (рис. 318).

В этом случае за оси координат следует

принять оси симметрии шестиугольника —

х и у. Для построения изометрической

проекции от начала аксонометрических

осей — точки О' по оси х' отложены отрез-

ки О'А' = 0'D' = ОА (коэффициенты ис-

141

К А

Л7"/772

/ 2

Г/

Хл

>г'У

Рис. 320

кажения по всем осям приняты равными

единице).

Замечая, что оставшиеся вершины по-

парно симметричны относительно осей ко-

ординат, от точки О' по оси у' откладыва-

ют отрезки О'—/' и О'—2', равные друг

другу и отрезкам О—/ и О—2.

Через точки Г и 2' проводят прямые,

параллельные оси х', на которых остается

определить положение точек В', С', Е', F',

что и сделано с помощью равных отрезков

l'-B', Г—С', 2'—Е', 2'—F', длины кото-

рых соответствуют координате х вершин В,

С, Е и F шестиугольника.

Пример 2. Построить прямоугольную

диметрическую проекци^о кривой т, рас-

положенной в плоскости хОг (рис. 319).

Аксонометрическую проекцию плоской

кривой строят по координатам отдельных

точек. Так, на заданной кривой т были

намечены точки 1,2, 3 и т. д. и определены

их прямоугольные координаты. Переходя

к аксонометрическому чертежу, -следует

учитывать коэффициенты искажения.

В нашем случае u=w— 1, а потому аксо-

нометрические координаты каждой точки

кривой равны прямоугольным.

Перейдем к построению аксонометрии

объемных предметов.

Пример 3. Построить прямоугольную

изометрическую проекцию усеченной шес-

тиугольной призмы со сквозным прямоу-

гольным отверстием (рис. 320).

Прежде всего на ортогональном черте-

же нанесем систему осей координат хуг,

так чтобы их начало оказалось в центре

основания призмы.

Опустим описание процесса построения

вторичной проекции призмы, иначе при-

дется дословно повторить текст первого

примера, в котором был построен правиль-

ный шестиугольник.

Отметим лишь, что две линии невидимо-

го контура А\В\ и C\D'i соответствуют

сквозному прямоугольному отверстию.

Следующий этап работы — создание аксо-

нометрического изображения призмы —

начинается с того, что через точки 1\, 2\,

... , 6\, А\, В\, С\, D] вторичной проекции

проводят вертикальные прямые, на кото-

рых затем откладывают отрезки, равные

Z|, Z

26, 2л и 2£.

Полученные точки (верхние концы вер-

тикальных отрезков) соединяют прямыми

так, чтобы обеспечить соответствие между

ортогональным и аксонометрическим изо-

бражениями призмы.

На рис. 320 это взаимно однозначное

соответствие иллюстрируется точками А и

Е и отрезком, который их соединяет.

Пример 4. Построить прямоугольную

диметрическую проекцию узла железобе-

тонной колонны (рис. 321).

На ортогональном чертеже оси коорди-

нат располагаем так, чтобы узел оказался

Рис.

453

143

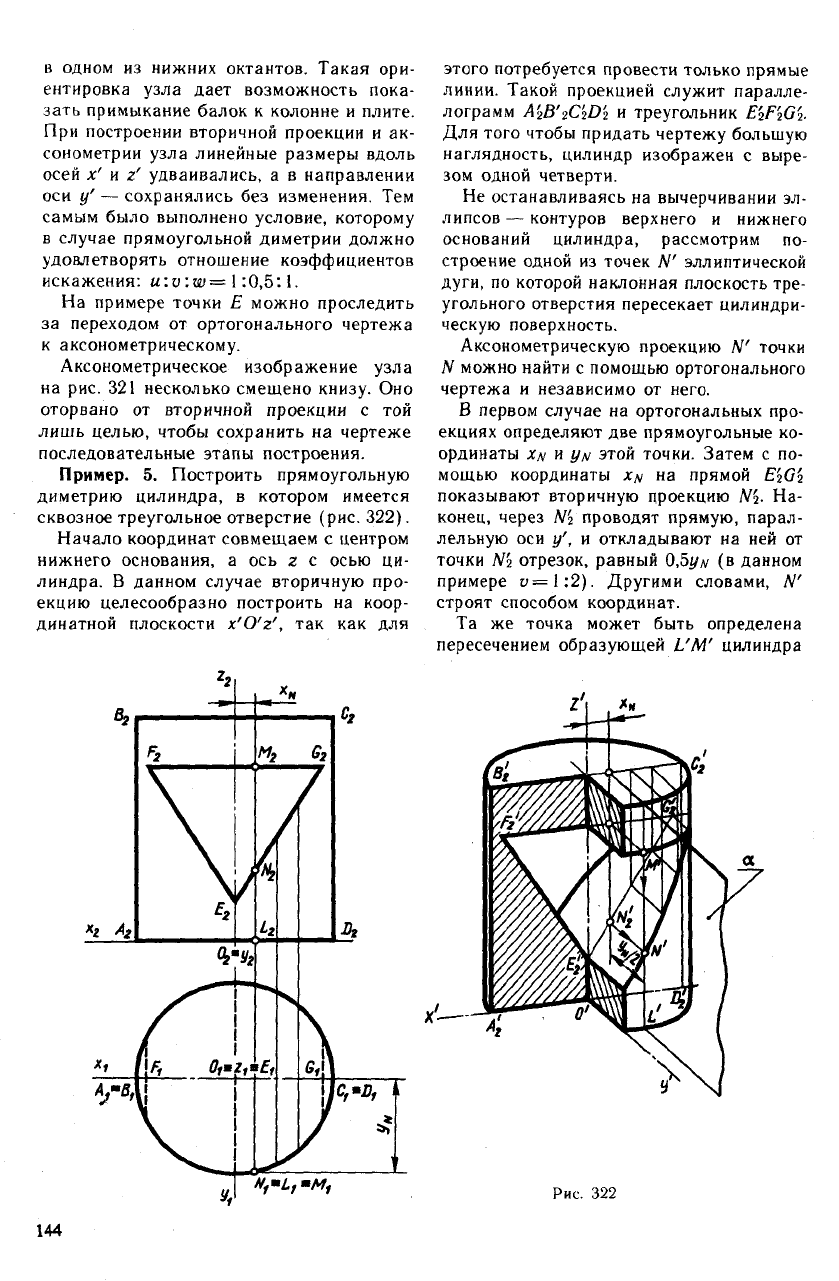
в одном из нижних октантов. Такая ори-

ентировка узла дает возможность пока-

зать примыкание балок к колонне и плите.

При построении вторичной проекции и ак-

сонометрии узла линейные размеры вдоль

осей х' и г' удваивались, а в направлении

оси у' — сохранялись без изменения. Тем

самым было выполнено условие, которому

в случае прямоугольной диметрии должно

удовлетворять отношение коэффициентов

искажения: u:v \w— 1:0,5:1.

На примере точки Е можно проследить

за переходом от ортогонального чертежа

к аксонометрическому.

Аксонометрическое изображение узла

на рис. 321 несколько смещено книзу. Оно

оторвано от вторичной проекции с той

лишь целью, чтобы сохранить на чертеже

последовательные этапы построения.

Пример. 5. Построить прямоугольную

диметрию цилиндра, в котором имеется

сквозное треугольное отверстие (рис. 322).

Начало координат совмещаем с центром

нижнего основания, а ось г с осью ци-

линдра. В данном случае вторичную про-

екцию целесообразно построить на коор-

динатной плоскости x'O'z', так как для

этого потребуется провести только прямые

линии. Такой проекцией служит паралле-

лограмм A'zB'iC'iD'i и треугольник E2F2G2.

Для того чтобы придать чертежу большую

наглядность, цилиндр изображен с выре-

зом одной четверти.

Не останавливаясь на вычерчивании эл-

липсов — контуров верхнего и нижнего

оснований цилиндра, рассмотрим по-

строение одной из точек N' эллиптической

дуги, по которой наклонная плоскость тре-

угольного отверстия пересекает цилиндри-

ческую поверхность.

Аксонометрическую проекцию N' точки

N можно найти с помощью ортогонального

чертежа и независимо от него.

В первом случае на ортогональных про-

екциях определяют две прямоугольные ко-

ординаты Хн и ун этой точки. Затем с по-

мощью координаты х\ на прямой E2G2

показывают вторичную проекцию Ы'ъ На-

конец, через N'2 проводят прямую, парал-

лельную оси у', и откладывают на ней от

точки

N'2

отрезок, равный 0,5ум (в данном

примере и=1:2). Другими словами, N'

строят способом координат.

Та же точка может быть определена

пересечением образующей L'M' цилиндра

Рис.

300

144

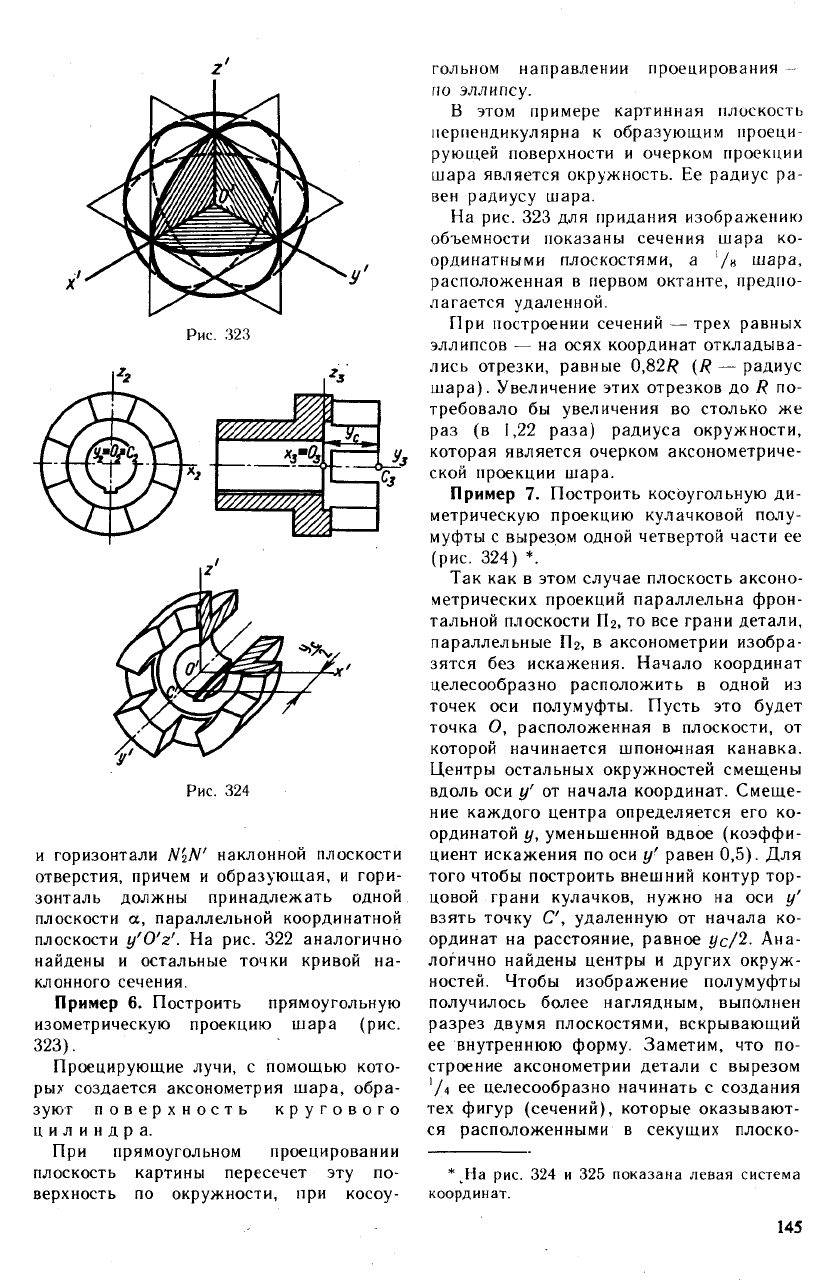
Рис. 323

Рис. 324

и горизонтали NW наклонной плоскости

отверстия, причем и образующая, и гори-

зонталь должны принадлежать одной

плоскости ос, параллельной координатной

плоскости у'О'г'. На рис. 322 аналогично

найдены и остальные точки кривой на-

клонного сечения.

Пример 6. Построить прямоугольную

изометрическую проекцию шара (рис.

323).

Проецирующие лучи, с помощью кото-

рых создается аксонометрия шара, обра-

зуют поверхность кругового

цилиндра.

При прямоугольном проецировании

плоскость картины пересечет эту по-

верхность по окружности, при косоу-

гольном направлении проецирования

по эллипсу.

В этом примере картинная плоскость

перпендикулярна к образующим проеци-

рующей поверхности и очерком проекции

шара является окружность. Ее радиус ра-

вен радиусу шара.

На рис. 323 для придания изображению

объемности показаны сечения шара ко-

ординатными плоскостями, а '/» шара,

расположенная в первом октанте, предпо-

лагается удаленной.

При построении сечений — трех равных

эллипсов — на осях координат откладыва-

лись отрезки, равные 0,82R (R — радиус

шара). Увеличение этих отрезков до R по-

требовало бы увеличения во столько же

раз (в 1,22 раза) радиуса окружности,

которая является очерком аксонометриче-

ской проекции шара.

Пример 7. Построить косоугольную ди-

метрическую проекцию кулачковой полу-

муфты с вырезом одной четвертой части ее

(рис. 324) *.

Так как в этом случае плоскость аксоно-

метрических проекций параллельна фрон-

тальной плоскости Пг, то все грани детали,

параллельные Пг, в аксонометрии изобра-

зятся без искажения. Начало координат

целесообразно расположить в одной из

точек оси полумуфты. Пусть это будет

точка О, расположенная в плоскости, от

которой начинается шпоночная канавка.

Центры остальных окружностей смещены

вдоль оси у' от начала координат. Смеще-

ние каждого центра определяется его ко-

ординатой у, уменьшенной вдвое (коэффи-

циент искажения по оси у

{

равен 0,5). Для

того чтобы построить внешний контур тор-

цовой грани кулачков, нужно на оси у'

взять точку С', удаленную от начала ко-

ординат на расстояние, равное ус/2. Ана-

логично найдены центры и других окруж-

ностей. Чтобы изображение полумуфты

получилось более наглядным, выполнен

разрез двумя плоскостями, вскрывающий

ее внутреннюю форму. Заметим, что по-

строение аксонометрии детали с вырезом

'/4 ее целесообразно начинать с создания

тех фигур (сечений), которые оказывают-

ся расположенными в секущих плоско-

* На рис. 324 и 325 показана левая система

координат.

145

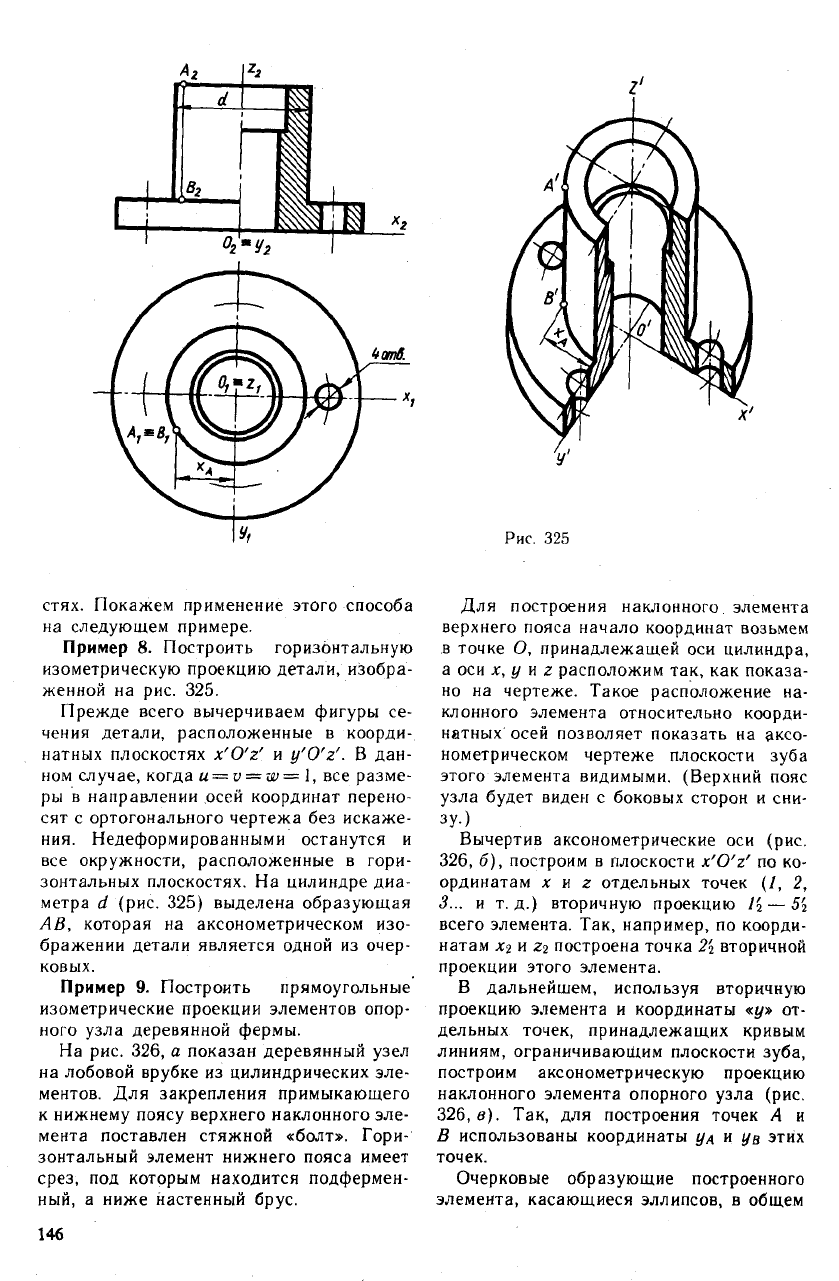
Рис. 325

стях. Покажем применение этого способа

на следующем примере.

Пример 8. Построить горизонтальную

изометрическую проекцию детали, изобра-

женной на рис. 325.

Прежде всего вычерчиваем фигуры се-

чения детали, расположенные в коорди-

натных плоскостях x'O'z' и y'O'z'. В дан-

ном случае, когда u = v — w— 1, все разме-

ры в направлении осей координат перено-

сят с ортогонального чертежа без искаже-

ния. Недеформированными останутся и

все окружности, расположенные в гори-

зонтальных плоскостях. На цилиндре диа-

метра d (рис. 325) выделена образующая

АВ, которая на аксонометрическом изо-

бражении детали является одной из очер-

ковых.

Пример 9. Построить прямоугольные

изометрические проекции элементов опор-

ного узла деревянной фермы.

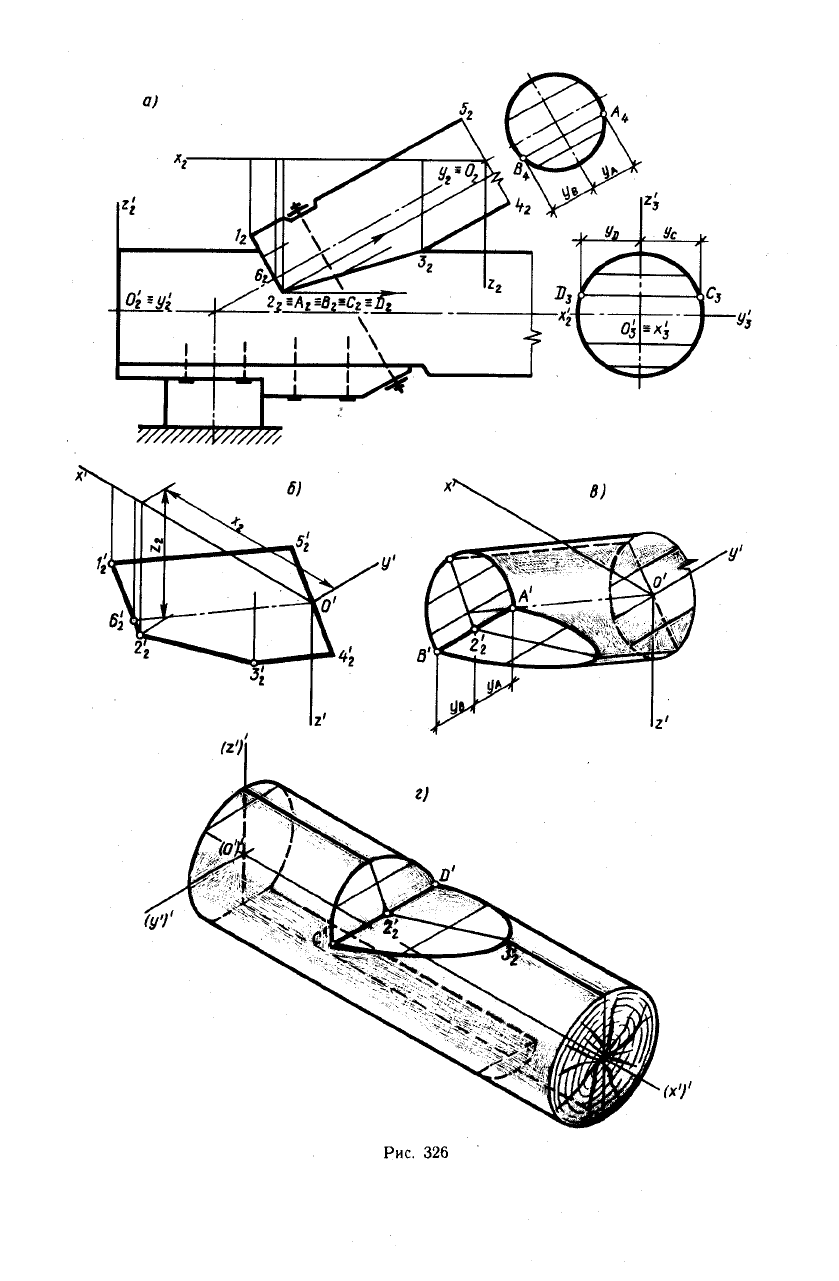
На рис. 326, а показан деревянный узел

на лобовой врубке из цилиндрических эле-

ментов. Для закрепления примыкающего

к нижнему поясу верхнего наклонного эле-

мента поставлен стяжной «болт». Гори-

зонтальный элемент нижнего пояса имеет

срез, под которым находится подфермен-

ный, а ниже настенный брус.

Для построения наклонного элемента

верхнего пояса начало координат возьмем

в точке О, принадлежащей оси цилиндра,

а оси х, у w z расположим так, как показа-

но на чертеже. Такое расположение на-

клонного элемента относительно коорди-

натных осей позволяет показать на аксо-

нометрическом чертеже плоскости зуба

этого элемента видимыми. (Верхний пояс

узла будет виден с боковых сторон и сни-

зу.)

Вычертив аксонометрические оси (рис.

326, б), построим в плоскости x'O'z' по ко-

ординатам х и z отдельных точек (1, 2,

3... и т.д.) вторичную проекцию /£ — 5'ч

всего элемента. Так, например, по коорди-

натам

Х2

и 22 построена точка

2'г

вторичной

проекции этого элемента.

В дальнейшем, используя вторичную

проекцию элемента и координаты «у» от-

дельных точек, принадлежащих кривым

линиям, ограничивающим плоскости зуба,

построим аксонометрическую проекцию

наклонного элемента опорного узла (рис.

326, в). Так, для построения точек А и

В использованы координаты </д и ув этих

точек.

Очерковые образующие построенного

элемента, касающиеся эллипсов, в общем

146

Ув

, Ус 1

/ У

.г,

\ Oi

Рис. 320

случае не совпадают с линиями вторичной

проекции. На приведенном чертеже гнездо

под стяжной болт не показано.

Аналогично выполнено построение и

второго — горизонтального элемента узла

(рис. 326, г). Для его построения начало

координат взято уже в другой точке — О'

Следует заметить, что при построении ак-

сонометрии этого элемента его вторичную

проекцию можно было расположить в

плоскости (г

)' (О

)' (у')'.

Аксонометрические проекции подфер-

менного бруса и настенного не приводятся.

Вопросы и задачи для самоконтроля

1. На чем основана классификация аксоно-

метрических проекций?

2. Что называется коэффициентом искаже-

ния?

3. Назовите стандартные аксонометрические

проекции.

4. Что представляет собой вторичнар проек-

ция геометрической фигуры?

Рис. 327

Рис.

300

Рис. 330

5. Построить вторичную проекцию прямой,

Прямоугольная изометрия которой является

точкой.

6. Провести прямую BDea(A,B,C,), парал-

лельную плоскости хОу (рис. 327).

7. Построить вторичную проекцию тетраэдра

SABC, если УА — Q, АВ\\хОу, SBC||xC>2 (рис.

328).

8. Определить координаты точек А и В, распо-

ложенных соответственно на поверхности конуса

и цилиндра (рис. 329).

9. Дано аксонометрическое изображение

прямоугольного параллелепипеда. Построить

его сечение плоскостью, заданной точками А,

В и С (рис. 330).

ГЛАВА 13

ЛИНЕЙНАЯ ПЕРСПЕКТИВА

§ 67. СУЩНОСТЬ МЕТОДА

Перспектива представляет собой

способ изображения тел и плоских фигур,

основанный на применении централ ь-

148

ного проецирования* (см. «Введе-

ние»). Для построения перспективы пред-

мета из некоторой точки S (точки зрения)

проводят лучи ко всем точкам изображае-

мого предмета. На пути проецирующих

лучей располагают поверхность 11' (карти-

ну), на которой строят искомое изображе-

ние, определяя точки пересечения лучей

с поверхностью картины. На рис. 331 пока-

зан принцип построения перспективы

предмета на плоскости (линейная перспек-

тива) .

Изображение предметов при помощи

центрального проецирования отличается

хорошей наглядностью. Перспекти-

ва предмета соответствует (с некоторым

приближением) тому, что видит глаз чело-

века, т. е. она передает кажущиеся изме-

нения величины и формы изображаемого

предмета, вызванные его расположением

и удаленностью от наблюдателя. Объясня-

ется это тем, что процесс зрения в гео-

метрическом отношении тождествен с ме-

тодом центрального проецирования. Еще

на стадии проектирования перспектива по-

зволяет выявить недостатки архитектур-

ной композиции строительного объекта

или комплекса и внести в нее соответству-

ющие коррективы.

Развитию теории перспективы и ее при-

ложений способствовали труды С. М. Ко-

лотова [9], Ю. Н. Короева [10], Н. А. Со-

болева, М. В. Федорова [17] и их последо-

вателей.

Этому же способствовали и большие

возможности современных ЭЦВМ, с по-

мощью которых удается успешно решать

задачи автоматизации чертежно-графиче-

ских работ, в том числе и построение пер-

спектив.

Работы А. Ф. Бабушкиной, В. С. Поло-

зова, Р. А. Резникова, В. Н. Семенова сви-

детельствуют о многообещающих резуль-

татах применения машинной графики при

* Perspectus (лат.) — увиденный насквозь,

ясно увиденный. Перспективой называ-

ют и само изображение предметов, построенное

в соответствии с тем кажущимся изменением их

величины и очертаний, которое обусловлено

удаленностью предметов от точки наблюдения

и их положением в пространстве.

SJLW

Рис. 331

построении перспектив на вертикальной

и наклонной картине.

Библиография, содержащая обширный

перечень статей, опубликованных за по-

следнее время в области теории перспек-

тивы, приведена Н. А. Соболевым в работе

[16].

Поверхность, на которой создают пер-

спективное изображение, может быть и не

плоской, а цилиндрической или сфериче-

ской. В первом случае перспектива назы-

вается панорамной, во втором — ку-

польной. Предметом нашего изучения

будет только линейная перспектива на

вертикальной плоскости.

При рассмотрении центрального прое-

цирования было установлено, что одна

центральная проекция точки (а значит,

и предмета) не определяет ее положения

в пространстве. Действительно, каждой

точке А' на плоскости П' (см. рис. 331)

соответствует любая точка проецирующе-

го луча SJ4'.

Для того чтобы обеспечить взаимную

однозначность между точками изображае-

мого предмета и точками на картинной

плоскости (сделать изображение обрати-

мым), поступают следующим образом. За-

данную точку А (рис. 332) ортогонально

проецируют на горизонтальную плоскость

III, перпендикулярную плоскости ГГ, а за-

тем на плоскости картины определяют пер-

спективные , (центральные) проекции как

точки А, так и ее горизонтальной проекции

А\. На рис. 332 луч, направленный в А,

пересекает картину в точке А', которая

является перспективной проек-

цией (перспективой) точки А. Вто-

рой луч, идущий в А), пересекая картину

149