Крылов Н.Н., ред. Начертательная геометрия
Подождите немного. Документ загружается.

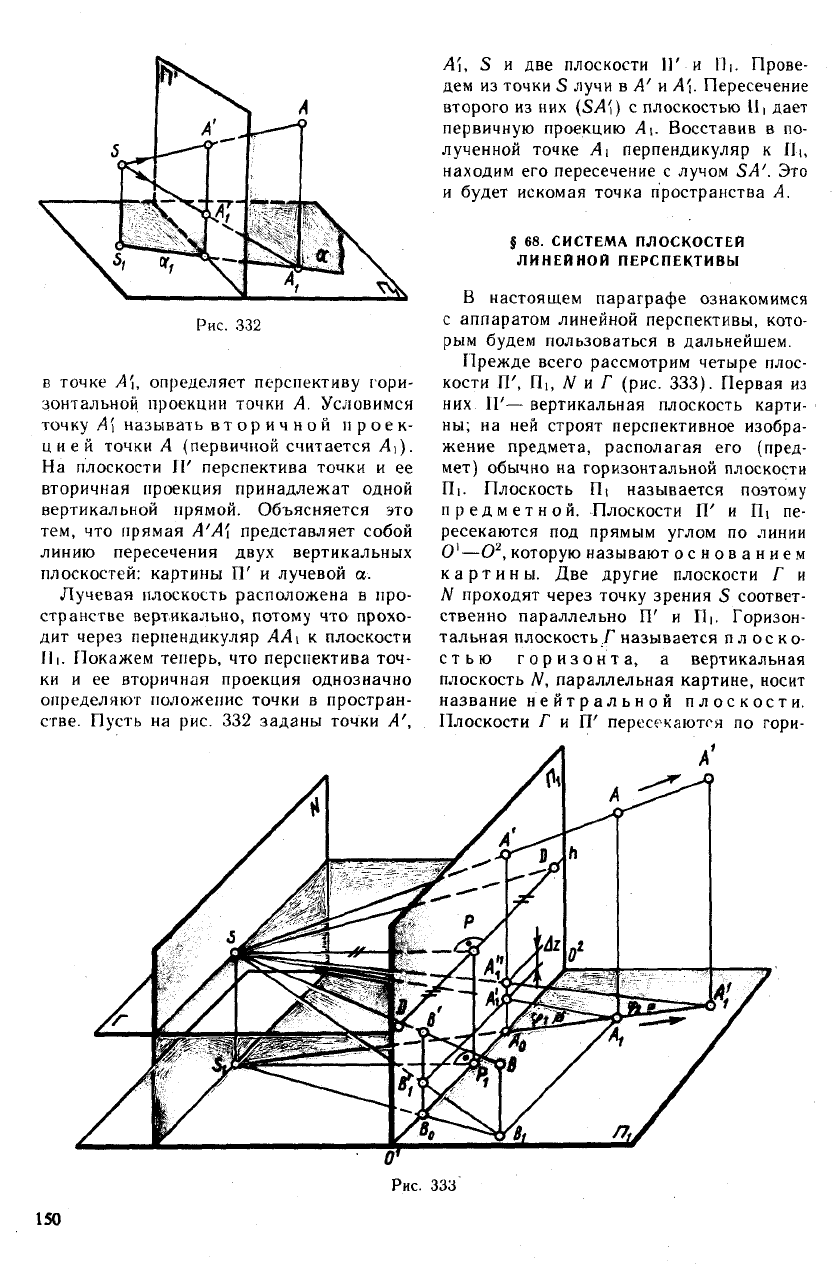
Рис. 332
в точке А\, определяет перспективу гори-
зонтальной проекции точки А. Условимся
точку А\ называть вторичной проек-
цией точки А (первичной считается Ai)-
На плоскости Л/ перспектива точки и ее
вторичная проекция принадлежат одной
вертикальной прямой. Объясняется это
тем, что прямая А'А\ представляет собой
линию пересечения двух вертикальных
плоскостей: картины П' и лучевой а.
Лучевая плоскость расположена в про-
странстве вертикально, потому что прохо-
дит через перпендикуляр АА\ к плоскости
Mi. Покажем теперь, что перспектива точ-
ки и ее вторичная проекция однозначно
определяют положение точки в простран-
стве. Пусть на рис. 332 заданы точки А',
А'\, S и две плоскости II'-и П|. Прове-
дем из точки S лучи в Л' и А\. Пересечение
второго из них (SA') с плоскостью II| дает
первичную проекцию А\. Восставив в по-
лученной точке А1 перпендикуляр к IIi,
находим его пересечение с лучом S/4'. Это
и будет искомая точка пространства А.
§ 68. СИСТЕМА ПЛОСКОСТЕЙ
ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ
В настоящем параграфе ознакомимся
с аппаратом линейной перспективы, кото-
рым будем пользоваться в дальнейшем.
Прежде всего рассмотрим четыре плос-
кости ГГ, П1, N и Г (рис. 333). Первая из
них II'— вертикальная плоскость карти-
ны; на ней строят перспективное изобра-
жение предмета, располагая его (пред-
мет) обычно на горизонтальной плоскости
Пь Плоскость П| называется поэтому
предметной. Плоскости П' и П] пе-
ресекаются под прямым углом по линии
О
1
—О
2
, которую называют основанием
картины. Две другие плоскости Г и
N проходят через точку зрения S соответ-
ственно параллельно П' и П|. Горизон-
тальная плоскость/" называется плоско-
стью горизонта, а вертикальная
плоскость N, параллельная картине, носит
название нейтральной плоскости.
Плоскости Г и П' пересекаются по гори-
'.Az
А
1
А
h
0
1
—_<
[ft
л
к/
Рис.
300
Ли
150

зонтальной прямой h — линии гори-
зонта.
Опустим из точки зрения S перпендику-
ляры на картинную и предметную плоско-
сти. Луч SP-LI1', находясь в горизонталь-
ной плоскости Г, пересечет картину в точ-
ке Р, которая принадлежит линии гори-
зонта h. Луч SP называют главным,
а точку Р — главной точкой карти-
ны. Основание Si перпендикуляра, опу-
щенного из точки S на предметную плос-
кость, условимся называть точкой сто-
яния. В некоторых случаях приходится
пользоваться так называемыми дистан-
ционными точками D (точками
дальности), расположенными на линии го-
ризонта так, что DP = SP. Пространство,
ограниченное плоскостями П' и N, называ-
ется промежуточным пространством,
часть пространства перед зрителем за кар-
тиной — предметным пространством,
а пространство позади наблюдателя назы-
вают мнимым.
Для построения перспективы необходи-
мо знать положение точки зрения S отно-
сительно плоскостей П' и II].
§ 69. ПЕРСПЕКТИВЫ ТОЧЕК,
РАСПОЛОЖЕННЫХ В РАЗЛИЧНЫХ
ЧАСТЯХ ПРОСТРАНСТВА
Рассмотрим точку.Л в предметном про-
странстве (см. рис. 333) и проследим за
тем, как будут изменяться положения ее
перспективы и вторичной проекции при
движении самой точки Л вдоль проециру-
ющего луча 5Л. Пусть точка переместится
из положения А в А
1
. Ее перспектива
останется по-прежнему в точке А'. Что же
касается вторичной проекции, то она смес-
тится вертикально вверх на Дг. По мере
дальнейшего удаления точки А от плоско-
сти картины ее вторичная проекция будет
приближаться к линии горизонта, так как
угол наклона луча, определяющего вто-
ричную проекцию, при таком перемещении
уменьшается (фг<ф,). В пределе, когда
точка А удалится в бесконечность, угол ф
будет равен нулю и луч, направленный
в горизонтальную проекцию бесконечно
удаленной точки, окажется в плоскости Г.
Следовательно, вторичная проекция
бесконечно удаленной точки предметного .
пространства должна находиться на ли-
нии горизонта. Этот очень важный вы-
вод не раз будет использован в даль-
нейшем.
Сопоставляя положение точек Л и Л
1
от-
носительно плоскости картины с их вто-
ричными проекциями, заключаем, что чем
ближе точка к картине, тем меньше рас-
стояние от ее вторичной проекции до осно-
вания картины. Если две точки (Л и В)
равноудалены от плоскости картины, то их
вторичные проекции находятся на одина-
ковом расстоянии от основания картины
(см. рис. 333).
Действительно, в этом случае прямая
Л|В] параллельна основанию картины и в
треугольнике 1SiSi имеет место равенст-
Л,Ло В|В„
во двух отношении:
Л i5I
B|S.
Но так
Л,Л
0
AqA'I ,
д
. „
С1
В,Во
как ——=—— (из M.S.S) и ——
Я,о, о,о о,о,
BoB'i
(из AB,S,S), то
ЛрЛ1
=
ВрВ\
S,S
5,5
4
" 5,5
Откуда следует, что ЛоЛ, = ВоВ,.
На рис. 334 показано построение пер-
спектив и вторичных проекций точек, рас-
положенных в промежуточном (точка В)
и мнимом (точка Е) пространствах. Вто-
ричные проекции точек промежуточ-
ного пространства оказываются ниже
основания картины (например, В\). Если
же точки принадлежат мнимому про-
странству, то их вторичные проекции рас-
положены выше линии горизонта (на-
пример, Е\). Вторичные проекции точек
предметного пространства могут быть рас-
положены только между основанием кар-
тины и линией горизонта (см. рис. 333).
Наконец, на основании картины находятся
вторичные проекции точек, лежащих на
картинной плоскости (например, точка
М на рис. 334). Что касается линии гори-
зонта, то она представляет собой множе-
ство вторичных проекций несобственных
точек пространства. Таким образом, по
вторичной проекции точки можно устано-
вить, в каком пространстве находится дан-
ная точка.
В дальнейшем условимся обозначать
точки пространства прописными буквами
(Л, В, £, ...), их перспективы теми же
буквами со штрихом (Л', В', Е', ...), а вто-
ричные проекции — с добавлением под-
строчного индекса (Л{, В1, Е\,
•
••)•
151
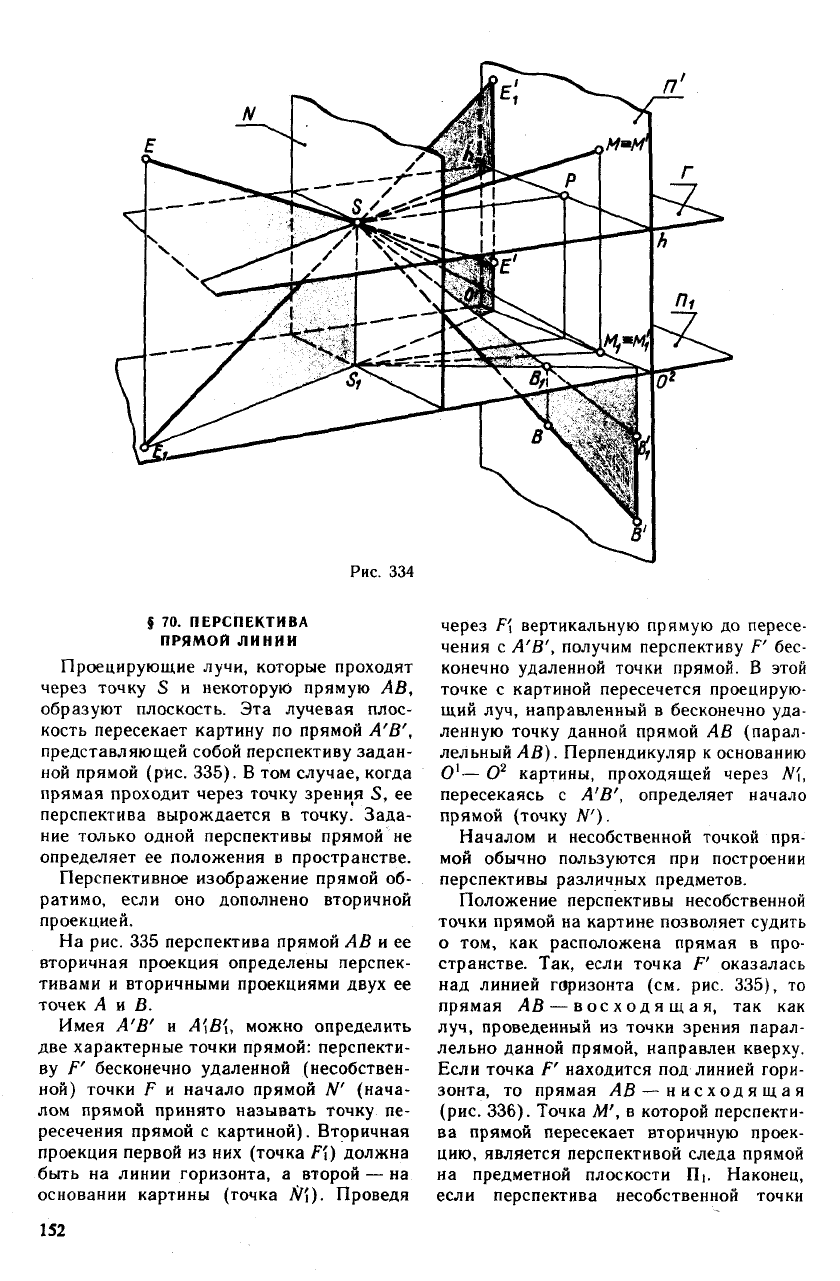
Рис. 334
§ 70. ПЕРСПЕКТИВА
ПРЯМОЙ ЛИНИИ
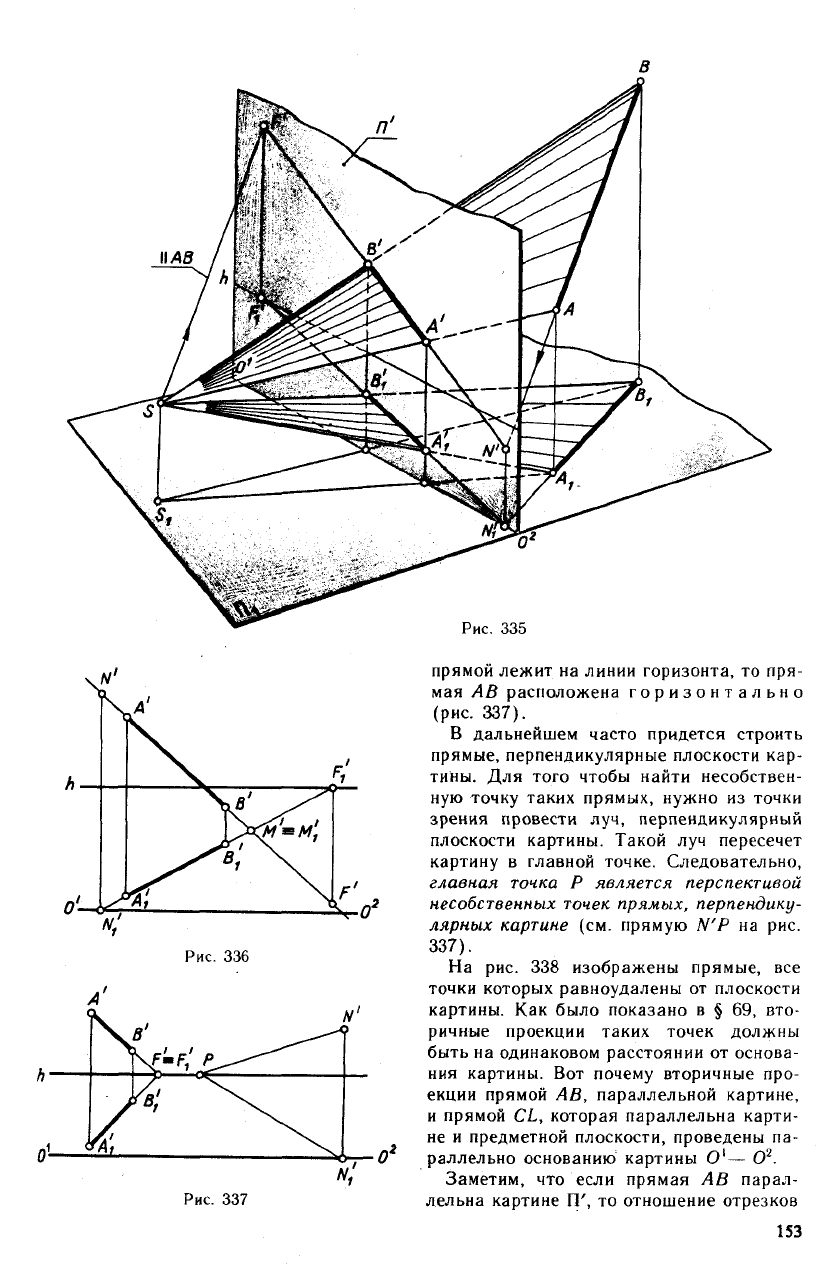
Проецирующие лучи, которые проходят
через точку S и некоторую прямую АВ,
образуют плоскость. Эта лучевая плос-
кость пересекает картину по прямой А'В',
представляющей собой перспективу задан-
ной прямой (рис. 335). В том случае, когда
прямая проходит через точку зрения S, ее
перспектива вырождается в точку. Зада-
ние только одной перспективы прямой не
определяет ее положения в пространстве.
Перспективное изображение прямой об-
ратимо, если оно дополнено вторичной
проекцией.
На рис. 335 перспектива прямой АВ и ее
вторичная проекция определены перспек-
тивами и вторичными проекциями двух ее
точек А я В.
Имея А'В' и
А'\В'\,
можно определить
две характерные точки прямой: перспекти-
ву F' бесконечно удаленной (несобствен-
ной) точки F и начало прямой N' (нача-
лом прямой принято называть точку пе-
ресечения прямой с картиной). Вторичная
проекция первой из них (точка ft) должна
быть на линии горизонта, а второй — на
основании картины (точка fi]5). Проведя
через F\ вертикальную прямую до пересе-
чения с А'В', получим перспективу F' бес-
конечно удаленной точки прямой. В этой
точке с картиной пересечется проецирую-
щий луч, направленный в бесконечно уда-
ленную точку данной прямой АВ (парал-
лельный АВ). Перпендикуляр к основанию
О
1
— О
2
картины, проходящей через N\,
пересекаясь с А'В', определяет начало
прямой (точку N').
Началом и несобственной точкой пря-
мой обычно пользуются при построении
перспективы различных предметов.
Положение перспективы несобственной
точки прямой на картине позволяет судить
о том, как расположена прямая в про-
странстве. Так, если точка F' оказалась
над линией горизонта (см. рис. 335), то
прямая АВ — восходящая, так как
луч, проведенный из точки зрения парал-
лельно данной прямой, направлен кверху.
Если точка F' находится под линией гори-
зонта, то прямая АВ — нисходящая
(рис. 336). Точка М', в которой перспекти-
ва прямой пересекает вторичную проек-
цию, является перспективой следа прямой
на предметной плоскости Пь Наконец,
если перспектива несобственной точки
152
в
прямой лежит на линии горизонта, то пря-
мая АВ расположена горизонтально
(рис. 337).
В дальнейшем часто придется строить
прямые, перпендикулярные плоскости кар-
тины. Для того чтобы найти несобствен-
ную точку таких прямых, нужно из точки
зрения провести луч, перпендикулярный
плоскости картины. Такой луч пересечет
картину в главной точке. Следовательно,
главная точка Р является перспективой
несобственных точек прямых, перпендику-
лярных картине (см. прямую N'P на рис.
337).
На рис. 338 изображены прямые, все
точки которых равноудалены от плоскости
картины. Как было показано в § 69, вто-
ричные проекции таких точек должны
быть на одинаковом расстоянии от основа-
ния картины. Вот почему вторичные про-
екции прямой АВ, параллельной картине,
и прямой CL, которая параллельна карти-
не и предметной плоскости, проведены па-
раллельно основанию картины О'— О
2
.
Заметим, что если прямая АВ парал-
лельна картине П', то отношение отрезков
153
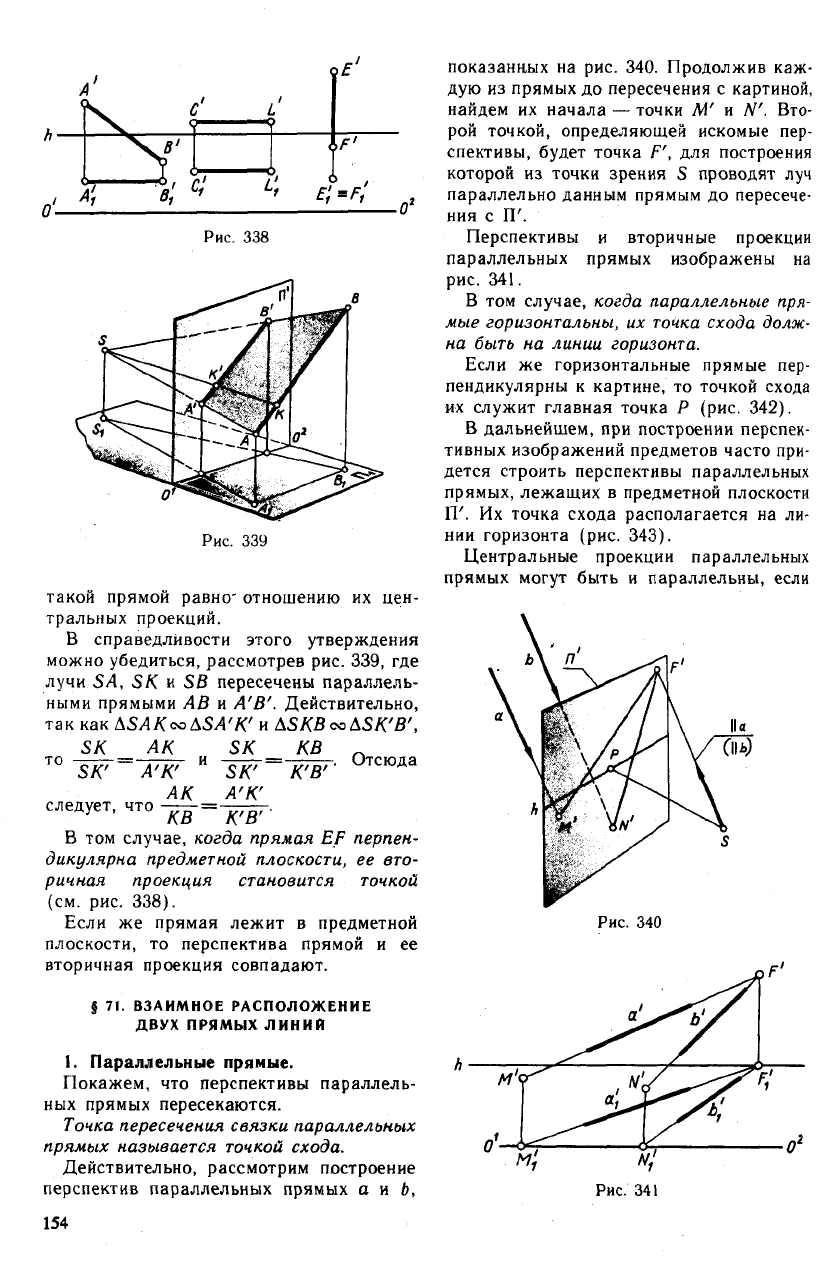
Рис. 338
Рис. 339
такой прямой равно" отношению их цен-
тральных проекций.
В справедливости этого утверждения
можно убедиться, рассмотрев рис. 339, где
лучи SA, SK и SB пересечены параллель-
ными прямыми АВ и А'В'. Действительно,
так как ASAKooASA'К' и ASKBooASK'B',
SK АК SK KB _
Отсюда
то — ,
SK' А'К'
АК
следует, что
SK'
А'К'
К'В'
показанных на рис. 340. Продолжив каж-
дую из прямых до пересечения с картиной,
найдем их начала — точки ЛГ и N'. Вто-
рой точкой, определяющей искомые пер-
спективы, будет точка F', для построения
которой из точки зрения S проводят луч
параллельно данным прямым до пересече-
ния с ГГ.
Перспективы и вторичные проекции
параллельных прямых изображены на
рис. 341.
В том случае, когда параллельные пря-
мые горизонтальны, их точка схода долж-
на быть на линии горизонта.
Если же горизонтальные прямые пер-
пендикулярны к картине, то точкой схода
их служит главная точка Р (рис. 342).
В дальнейшем, при построении перспек-
тивных изображений предметов часто при-
дется строить перспективы параллельных
прямых, лежащих в предметной плоскости
ГГ. Их точка схода располагается на ли-
нии горизонта (рис. 343).
Центральные проекции параллельных
прямых могут быть и параллельны, если
KB К'В'
В том случае, когда прямая EF перпен-
дикулярна предметной плоскости, ее вто-
ричная проекция становится точкой
(см. рис. 338).
Если же прямая лежит в предметной
плоскости, то перспектива прямой и ее
вторичная проекция совпадают.
§ 71. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПРЯМЫХ ЛИНИЙ
1. Параллельные прямые.
Покажем, что перспективы параллель-
ных прямых пересекаются.
Точка пересечения связки параллельных
прямых называется точкой схода.
Действительно, рассмотрим построение
перспектив параллельных прямых а и Ь,
Рис. 340
Рис.
300
154
К'
м'
^ А/ ^
Ai' 1 в;
L' ,
N'
ЦЧ
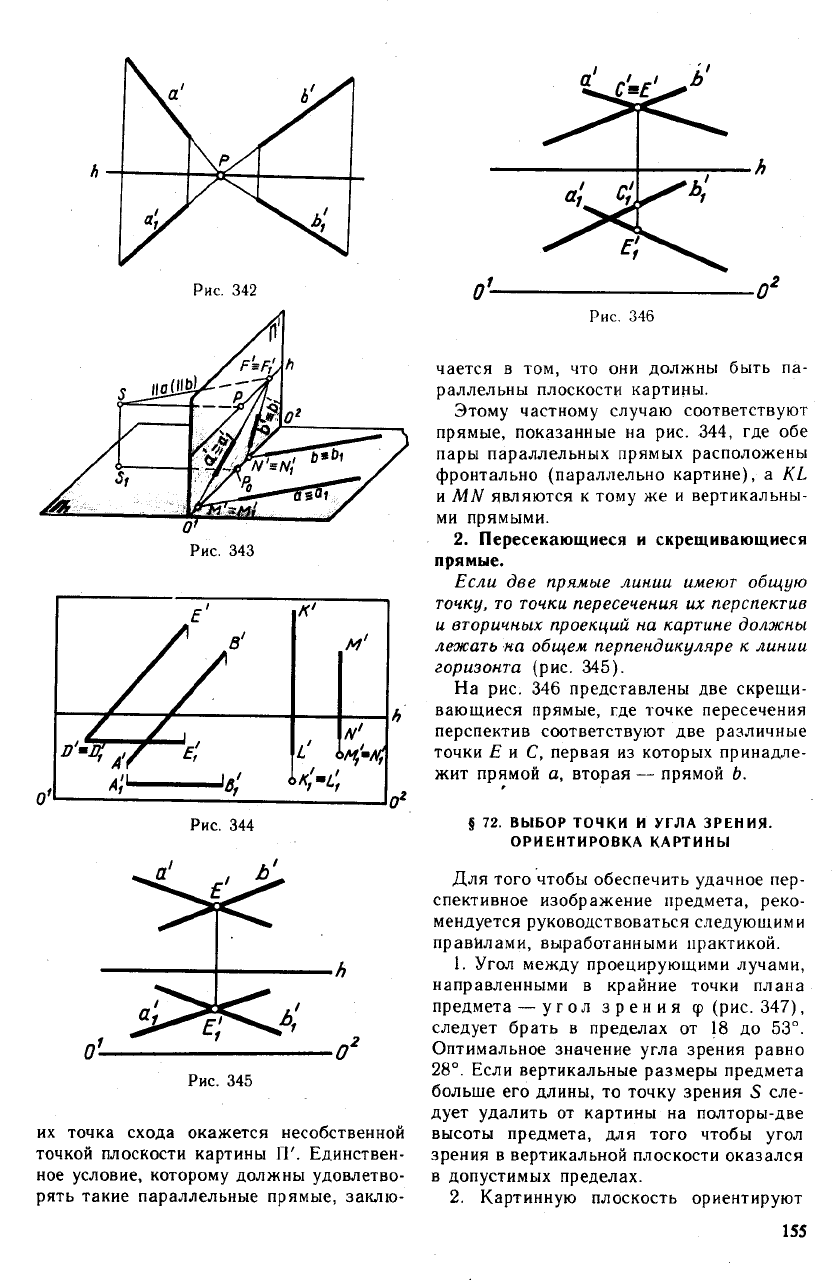
Рис. 344
h
А'
„2
Рис. 345
их точка схода окажется несобственной
точкой плоскости картины IT. Единствен-
ное условие, которому должны удовлетво-
рять такие параллельные прямые, заклю-
чается в том, что они должны быть па-
раллельны плоскости картины.
Этому частному случаю соответствуют
прямые, показанные на рис. 344, где обе
пары параллельных прямых расположены
фронтально (параллельно картине), a KL
и MN являются к тому же и вертикальны-
ми прямыми.
2. Пересекающиеся и скрещивающиеся
прямые.
Если две прямые линии имеют общую
точку, то точки пересечения их перспектив
и вторичных проекций на картине должны
лежать на общем перпендикуляре к линии
горизонта (рис. 345).
На рис. 346 представлены две скрещи-
вающиеся прямые, где точке пересечения
перспектив соответствуют две различные
точки £ и С, первая из которых принадле-
жит прямой а, вторая — прямой Ь.
§ 72. ВЫБОР ТОЧКИ И УГЛА ЗРЕНИЯ.
ОРИЕНТИРОВКА КАРТИНЫ
Для того чтобы обеспечить удачное пер-
спективное изображение предмета, реко-
мендуется руководствоваться следующими
правилами, выработанными практикой.
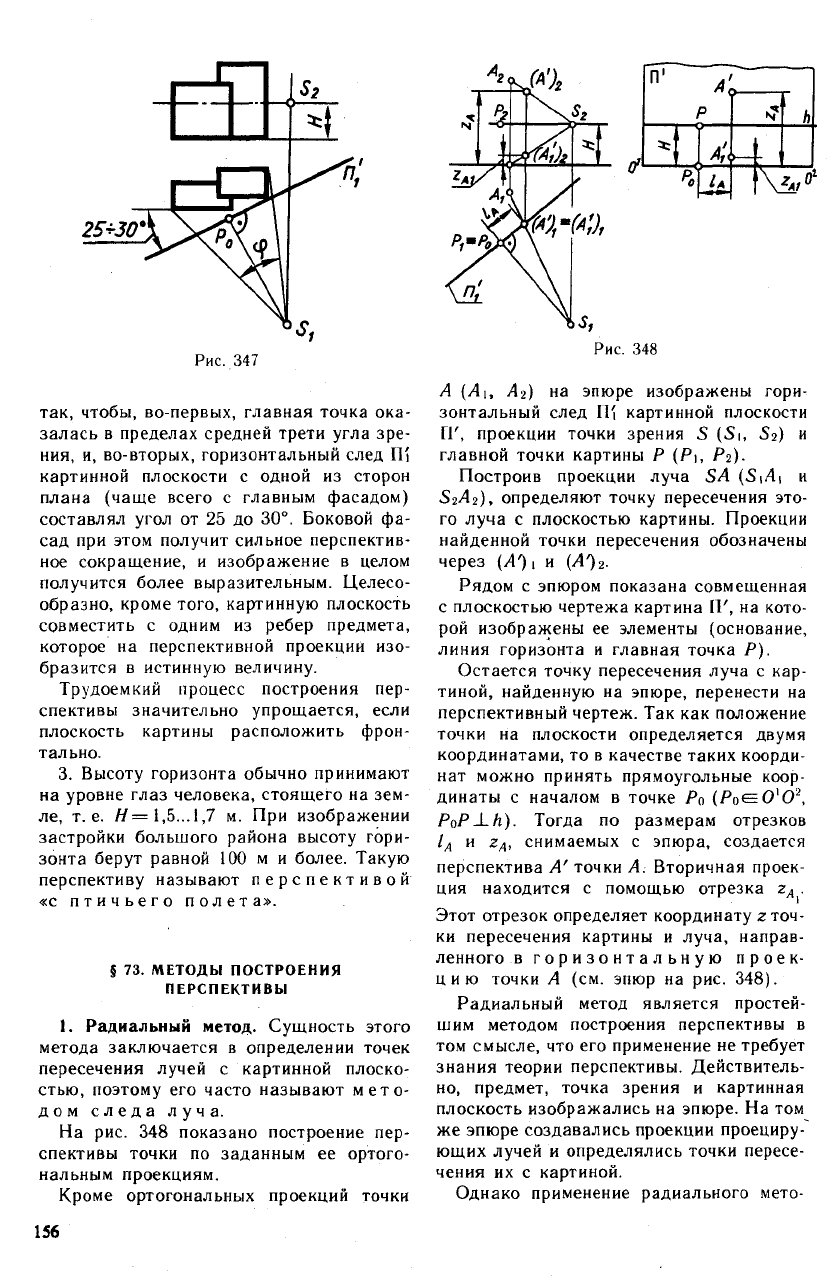
1. Угол между проецирующими лучами,
направленными в крайние точки плана
предмета — угол зрения ф (рис. 347),
следует брать в пределах от 18 до 53°.
Оптимальное значение угла зрения равно
28°. Если вертикальные размеры предмета
больше его длины, то точку зрения S сле-
дует удалить от картины на полторы-две
высоты предмета, для того чтобы угол
зрения в вертикальной плоскости оказался
в допустимых пределах.
2. Картинную плоскость ориентируют
155
так, чтобы, во-первых, главная точка ока-
залась в пределах средней трети угла зре-
ния, и, во-вторых, горизонтальный след III
картинной плоскости с одной из сторон
плана (чаще всего с главным фасадом)
составлял угол от 25 до 30°. Боковой фа-
сад при этом получит сильное перспектив-
ное сокращение, и изображение в целом
получится более выразительным. Целесо-
образно, кроме того, картинную плоскость
совместить с одним из ребер предмета,
которое на перспективной проекции изо-
бразится в истинную величину.
Трудоемкий процесс построения пер-
спективы значительно упрощается, если
плоскость картины расположить фрон-
тально.
3. Высоту горизонта обычно принимают
на уровне глаз человека, стоящего на зем-
ле, т.е. //=1,5...1,7 м. При изображении
застройки большого района высоту гори-
зонта берут равной 100 м и более. Такую
перспективу называют перспективой
«с птичьего полета».
§ 73. МЕТОДЫ ПОСТРОЕНИЯ
ПЕРСПЕКТИВЫ
1. Радиальный метод. Сущность этого
метода заключается в определении точек
пересечения лучей с картинной плоско-
стью, поэтому его часто называют мето-
дом следа луча.
На рис. 348 показано построение пер-
спективы точки по заданным ее ортого-
нальным проекциям.
Кроме ортогональных проекций точки
Л (Ai, Л2) на эпюре изображены гори-
зонтальный след 11| картинной плоскости
ГГ, проекции точки зрения S (Si, S2) и
главной точки картины Р (Рi, Рг)-
Построив проекции луча SA (S1Ai и
ЗгЛг), определяют точку пересечения это-
го луча с плоскостью картины. Проекции
найденной точки пересечения обозначены
через (ЛО
|
и (ЛОг-
Рядом с эпюром показана совмещенная
с плоскостью чертежа картина ГГ, на кото-
рой изображены ее элементы (основание,
линия горизонта и главная точка Р).
Остается точку пересечения луча с кар-
тиной, найденную на эпюре, перенести на
перспективный чертеж. Так как положение
точки на плоскости определяется двумя
координатами, то в качестве таких коорди-
нат можно принять прямоугольные коор-
динаты с началом в точке Ра (Ро^О'О
2
,
PoP-Lh). Тогда по размерам отрезков
1
А
и z
A
, снимаемых с эпюра, создается
перспектива А' точки Л. Вторичная проек-
ция находится с помощью отрезка г
А
.
Этот отрезок определяет координату z точ-
ки пересечения картины и луча, направ-
ленного в горизонтальную проек-
цию точки Л (см. эпюр на рис. 348).
Радиальный метод является простей-
шим методом построения перспективы в
том смысле, что его применение не требует
знания теории перспективы. Действитель-
но, предмет, точка зрения и картинная
плоскость изображались на эпюре. На том
же эпюре создавались проекции проециру-
ющих лучей и определялись точки пересе-
чения их с картиной.
Однако применение радиального мето-
156

да, включающего многократное повторе-
ние одних и тех же построений, требует
много времени и не обеспечивает должной
точности. Достаточно сказать, что для по-
строения перспективы отрезка прямой не-
обходимо проделать десять элементарных
операций, под которыми здесь следует по-
нимать проведение прямой по линейке и
построение отрезка, равного данному, с
помощью циркуля. Радиальный метод ока-
зывается рациональным при построении
перспективы предмета, в плане которого
имеется много не параллельных меж-
ду собой линий.
2. Метод архитекторов. В практике ра-
боты архитектурных мастерских широко
применяется метод построения перспек-
тивных изображений с использованием то-
чек схода параллельных прямых. Этот ме-
тод принято называть методом архи-
текторов.
Так как создание перспективы предмета
рекомендуется начинать с его вторичной
проекции, то сущность рассматриваемого
метода может быть показана на примере
построения перспективы фигуры, располо-
женной на горизонтальной плоскости.
Ортогональные проекции такой фигуры,
которую можно рассматривать как план
некоторого здания, представлены на рис.
349. На том же эпюре изображены гори-
зонтальный след картинной плоскости,
проекции точки зрения и главной точки
р (Ро).
Замечая, что линии контура плана могут
быть разделены на два пучка парал-
лельных прямых, определяем перспективы
несобственных точек (/•"' и F
2
) каждого из
пучков, причем точка F
1
является перспек-
тивой несобственной точки пучка парал-
лельных прямых направления /, а точка
Fнаправления //. Обе точки найдены
с помощью лучей SF
X
и SF
2
, соответствен-
но параллельных прямым направлений / и
//. Лучи SF
1
и SF
2
, будучи параллельными
прямым, расположенным в горизонталь-
ной плоскости, пересекут картину в точ-
ках, лежащих на линии горизонта h (рис.
350). При построении перспективы без
увеличения отрезки PF
X
и PF
2
на рис.
350 равны соответственно отрезкам PoF\
и P
0
F1 (см. рис. 349) *.
В качестве вторых точек для построения
перспективы каждой из прямых контура
рекомендуется использовать характерные
точки, в которых эти прямые пересекают
плоскость картины, т. е. начальные
точки прямых. Для этого горизонталь-
ные проекции всех прямых продолжены
до пересечения с одноименным следом П{
картины. Так найдены точки No, JVO, JVO,
N о и N о, расположенные на основании
картины.
Перенос этих точек с эпюра на картину
можно проделать с помощью полоски бу-
маги, которую следует приложить прямо-
линейной кромкой к следу Ш картины
и отметить на кромке точки No, No, No, No,
N о и Ро. Эту полоску бумаги переносим на
рис. 350 и совмещаем ее кромку с основа-
нием О
1
— О
2
картины так, чтобы точка Ро
на полоске совпала с той же точкой на
основании.
* На рис. 350 и некоторых последующих это
условие выполнено не строго по техническим
причинам.
157
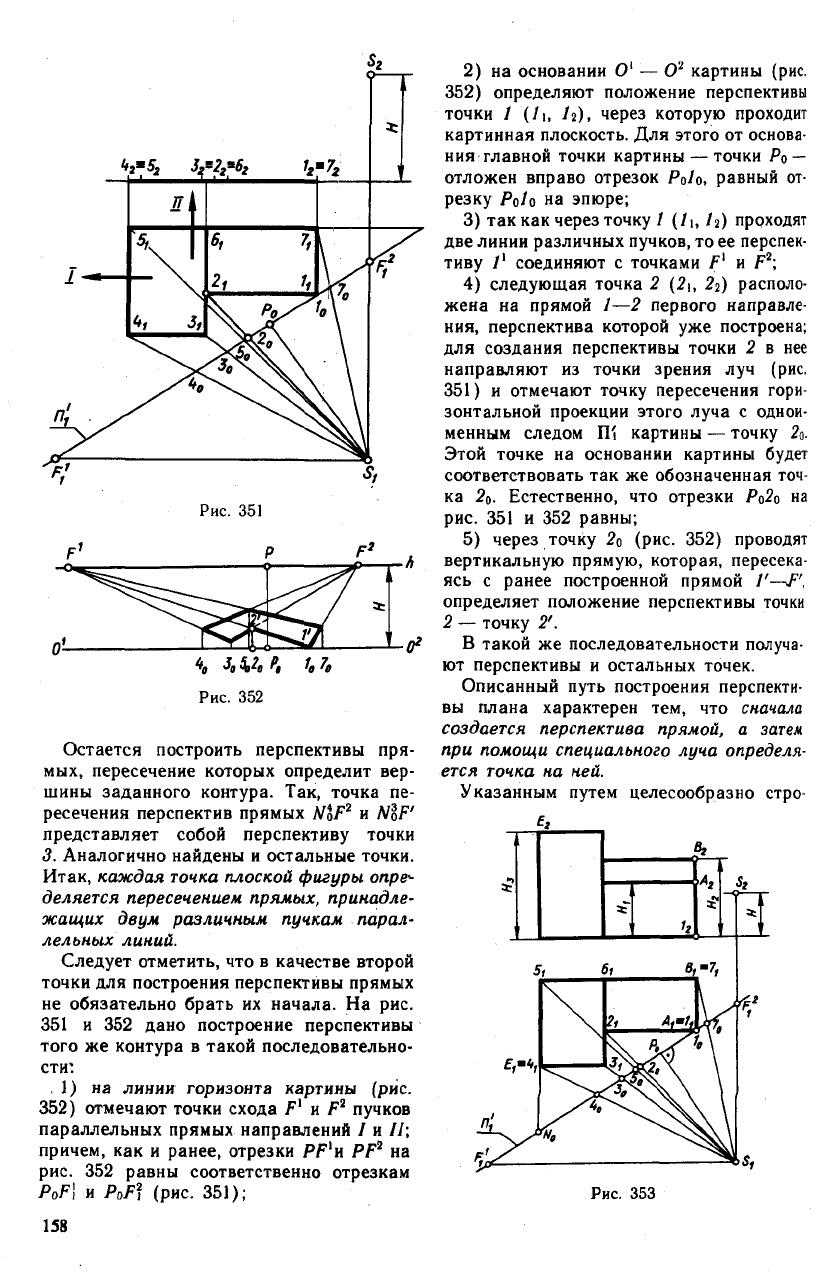
F
1
P F>
Остается построить перспективы пря-
мых, пересечение которых определит вер-
шины заданного контура. Так, точка пе-
ресечения перспектив прямых NoF
2
и NlF'
представляет собой перспективу точки
3. Аналогично найдены и остальные точки.
Итак, каждая точка плоской фигуры опре-
деляется пересечением прямых, принадле-
жащих двум различным пучкам парал-
лельных линий.
Следует отметить, что в качестве второй
точки для построения перспективы прямых
не обязательно брать их начала. На рис.
351 и 352 дано построение перспективы
того же контура в такой последовательно-
сти:
, 1) на линии горизонта картины (рис.
352) отмечают точки схода F
1
и F
2
пучков
параллельных прямых направлений / и //;
причем, как и ранее, отрезки PF
1
и
PF
2
на
рис. 352 равны соответственно отрезкам
PoF\ и P
a
F] (рис. 351);
2) на основании 0
х
— О
2
картины (рис.
352) определяют положение перспективы
точки 1 (I|, h), через которую проходит
картинная плоскость. Для этого от основа-
ния главной точки картины — точки Ро —
отложен вправо отрезок Polo, равный от-
резку Polo на эпюре;
3) так как через точку 1 (Л, /
2
) проходят
две линии различных пучков, то ее перспек-
тиву I
х
соединяют с точками F
x
и F
2
;
4) следующая точка 2 (21, 2г) располо-
жена на прямой /—2 первого направле-
ния, перспектива которой уже построена;
для создания перспективы точки 2 в нее
направляют из точки зрения луч (рис.
351) и отмечают точку пересечения гори-
зонтальной проекции этого луча с однои-
менным следом П1 картины — точку 2».
Этой точке на основании картины будет
соответствовать так же обозначенная точ-
ка 2
0
. Естественно, что отрезки Ро2о на
рис. 351 и 352 равны;
5) через точку 2о (рис. 352) проводят
вертикальную прямую, которая, пересека-
ясь с ранее построенной прямой l'—F',
определяет положение перспективы точки
2 — точку 2'.
В такой же последовательности получа-
ют перспективы и остальных точек.
Описанный путь построения перспекти-
вы плана характерен тем, что сначала
создается перспектива прямой, а затем
при помощи специального луча определя-
ется точка на ней.
158
ить перспективу плана в случае, когда
точки пересечения некоторых прямых с
картиной оказываются за пределами чер-
тежа.
Закончив построение вторичной проек-
ции, следует перейти к изображению само-
го предмета.
На рис. 353 даны ортогональные проек-
ции двух геометрических тел, план кото-
рых тождествен ранее рассмотренной фи-
гуре. Не повторяя объяснений, относящих-
ся к построению вторичной проекции,
опишем процесс создания перспективы
предмета.
Отметим только, что построение пер-
спективы предмета (как и его вторичной
проекции) в данном случае проведено с
увеличением всех линейных размеров на
картине в п раз. Это значит, что расстоя-
ние между основанием картины и линией
горизонта на рис. 354 равно не Н, как на
рис. 353, а пН. Отрезки PF
]
и PF
2
рис.
354 в п раз больше тех же отрезков на
эпюре и т. д.
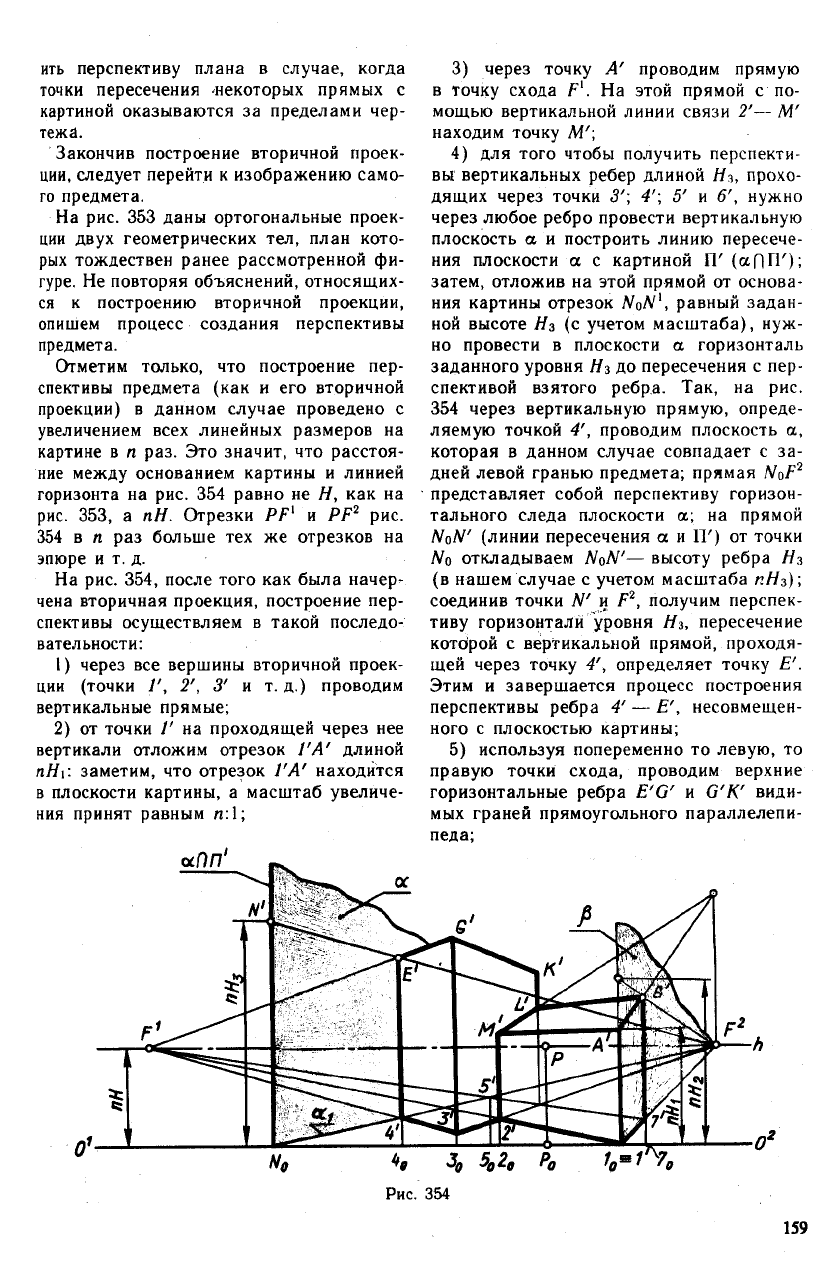
На рис. 354, после того как была начер-
чена вторичная проекция, построение пер-
спективы осуществляем в такой последо-
вательности:
1) через все вершины вторичной проек-
ции (точки /', 2', 3' и т. д.) проводим
вертикальные прямые;
2) от точки 1' на проходящей через нее
вертикали отложим отрезок 1'А' длиной
пНь заметим, что отрезок 1'А' находится
в плоскости картины, а масштаб увеличе-
ния принят равным п: 1;
осПп'
3) через точку А' проводим прямую
в точку схода F
1
. На этой прямой с по-
мощью вертикальной линии связи 2'— М'
находим точку М';
4) для того чтобы получить перспекти-
вы вертикальных ребер длиной Нз, прохо-
дящих через точки 3'\ 4'; 5' и 6', нужно
через любое ребро провести вертикальную
плоскость а и построить линию пересече-
ния плоскости а с картиной П' (af|IT);
затем, отложив на этой прямой от основа-
ния картины отрезок NоЛ/
1
, равный задан-
ной высоте Нз (с учетом масштаба), нуж-
но провести в плоскости а горизонталь
заданного уровня Нз до пересечения с пер-
спективой взятого ребра. Так, на рис.
354 через вертикальную прямую, опреде-
ляемую точкой 4', проводим плоскость а,
которая в данном случае совпадает с за-
дней левой гранью предмета; прямая NoF
2
представляет собой перспективу горизон-
тального следа плоскости а; на прямой
NoN' (линии пересечения а и IT) от точки
N о откладываем NoN'— высоту ребра Нз
(в нашем случае с учетом масштаба пНз)\
соединив точки N' и F
2
, получим перспек-
тиву горизонтали уровня Нз, пересечение
которой с вертикальной прямой, проходя-
щей через точку 4', определяет точку Е'.
Этим и завершается процесс построения
перспективы ребра 4' — £', несовмещен-
ного с плоскостью картины;
5) используя попеременно то левую, то
правую точки схода, проводим верхние
горизонтальные ребра E'G' и G'K' види-
мых граней прямоугольного параллелепи-
педа;
4
в 3
0
5
0
2„
Рис. 354
159
