Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

ственная прямой АВ. Эта прямая должна

пересечь прямую S<H в ее несобственной

точке, т. е. прямая СоВ' будет параллель-

на S(v4. Искомая точка В' должна при-

надлежать прямой СоВ'. Она определяется

как точка пересечения прямой СоВ' с прое-

цирующей линией SoB.

Гомология играет существенную роль

в теории линейной перспективы. Здесь ус-

танавливается соответствие между пер-

спективой фигуры и самой фигурой, при-

чем плоскость последней должна быть со-

вмещена с картиной.

f 3. ПЕРСПЕКТИВНО-АФФИННОЕ

(РОДСТВЕННОЕ) СООТВЕТСТВИЕ

Соответствие, которое устанавливается

между фигурами с помощью параллельной

проекции, называется перспективно-

аффинным.

Перспективно-аффинное соответствие

представляет собой частный случай пер-

спективной коллинеации, когда центром

проецирования является бесконечно уда-

ленная точка.

Родственному соответстию присущи об-

щие свойства перспективной коллинеации

и специфические свойства параллельного

проецирования.

Как и во всякой перспективной коллине-

ации, в родственном соответствии:

1) каждой точке А одной плоскости со-

ответствует родственная точка А' второй

плоскости (рис. 9) ;

2) каждой прямой а одной плоскости

соответствует родственная прямая а' вто-

рой плоскости;

3) родственные точки расположены на

прямых, проходящих через центр проек-

Рис. 9

ций (при бесконечно удаленном центре

проецирующие лучи будут параллельны);

4) родственные прямые а и а' пересека-

ются на оси родства, которой служит ли-

ния пересечения т данных плоскостей П

и П'. Эта ось является множеством двой-

ных точек;

5) сохраняются свойства принадлежно-

сти точек прямым, т. е. если точка К при-

надлежит прямой а, то родственная точка

К' принадлежит родственной прямой а'.

Кроме того, родственное соответствие

обладает следующими свойствами,

связанными с особым положением центра

проецирования:

1. Параллельным прямым одной плос-

кости соответствуют параллельные пря-

мые второй плоскости.

Проецирующие лучи, проходящие через

заданные параллельные прямые а и 6,

образуют две параллельные плоскости, ко-

торые пересекаются третьей плоскостью П'

по параллельным прямым а' и Ь'.

2. Отношение длин отрезков одной пря-

мой или параллельных прямых равно от-

ношению родственных им отрезков.

Рассмотрим сначала рис. 9, где показа-

ны соответствующие друг другу отрезки

АВ и А'В'.

Родственные прямые а и а', на которых

расположены заданные отрезки, образу-

ют угол с вершиной Со. Отрезки сторон

этого угла, заключенные между парал-

лельными прямыми АА', ВВ' и КК', удов-

летворяют условию АК-КВ=А'К''-К'В'.

Пусть теперь даны отрезки АВ и EF

двух параллельных прямых (рис. 10). Сое-

динив точки А и Е и проведя FC||i4£,

получим параллелограмм AEFC. В силу

предыдущего свойства (п. 2) четыреху-

гольник A'E'F'C' является также паралле-

лограммом, а потому A'C' = E'F'.

Но АВ:АС=А'В':А'С', а так как АС=

=EF и А'С'=E'F', то AB:EF=

=A'B':E'F'.

В начертательной геометрии перечис-

ленные свойства широко используются

при изображении тел и плоских фигур на

проекционных чертежах.

Родственное соответствие, установлен-

ное между двумя плоскостями при парал-

лельном проецировании, сохраняется при

их совмещении.

Но в этом случае прямые, соединяющие

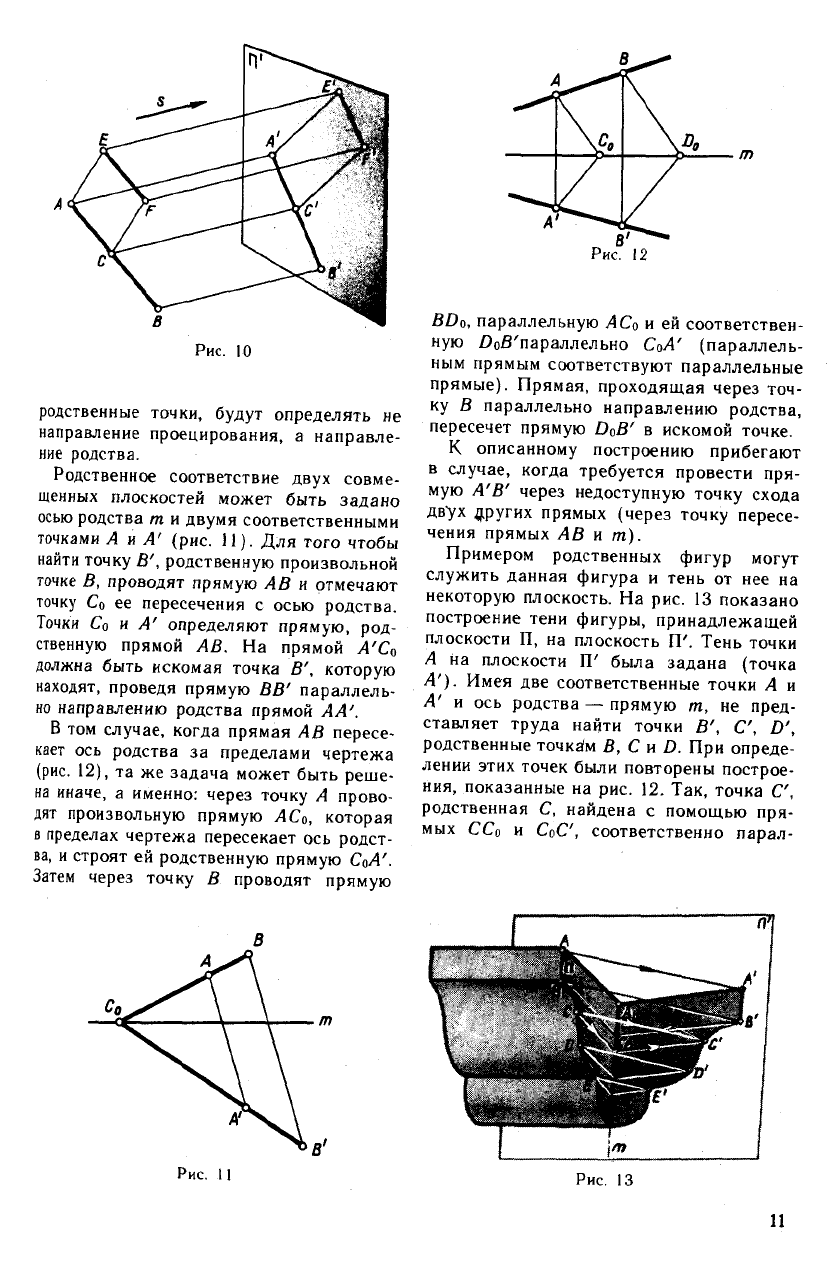
родственные точки, будут определять не

направление проецирования, а направле-

ние родства.

Родственное соответствие двух совме-

щенных плоскостей может быть задано

осью родства т и двумя соответственными

точками А и А' (рис. 11). Для того чтобы

найти точку В', родственную произвольной

точке 5, проводят прямую и отмечают

точку Со ее пересечения с осью родства.

Точки Со и /4' определяют прямую, род-

ственную прямой АВ. На прямой А'С

должна быть искомая точка В', которую

находят, проведя прямую ВВ' параллель-

но направлению родства прямой АА'.

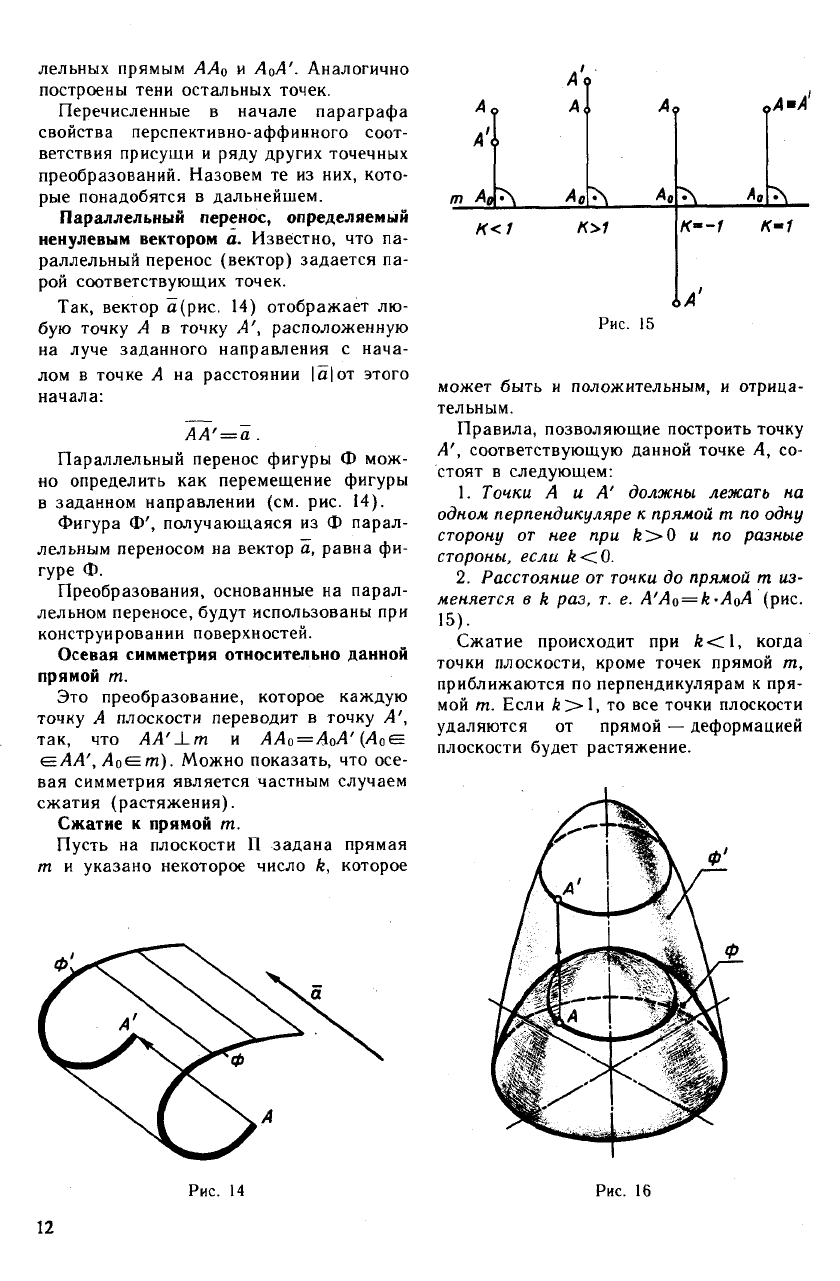
В том случае, когда прямая АВ пересе-

кает ось родства за пределами чертежа

(рис. 12), та же задача может быть реше-

на иначе, а именно: через точку А прово-

дят произвольную прямую АС

, которая

в пределах чертежа пересекает ось родст-

ва, и строят ей родственную прямую С

А'.

Затем через точку В проводят прямую

BDо, параллельную АСо и ей соответствен-

ную Лоб'параллельно СоА' (параллель-

ным прямым соответствуют параллельные

прямые). Прямая, проходящая через точ-

ку В параллельно направлению родства,

пересечет прямую DoB' в искомой точке.

К описанному построению прибегают

в случае, когда требуется провести пря-

мую А'В' через недоступную точку схода

дв"ух других прямых (через точку пересе-

чения прямых АВ и т).

Примером родственных фигур могут

служить данная фигура и тень от нее на

некоторую плоскость. На рис. 13 показано

построение тени фигуры, принадлежащей

плоскости П, на плоскость П'. Тень точки

А на плоскости П' была задана (точка

А'). Имея две соответственные точки А и

А' и ось родства — прямую т, не пред-

ставляет труда найти точки В', С', D',

родственные точка'м В, С и D. При опреде-

лении этих точек были повторены построе-

ния, показанные на рис. 12. Так, точка С',

родственная С, найдена с помощью пря-

мых ССо и СоС', соответственно парал-

7Р!

Рис.

131

Рис. 132 Рис. 133

лельных прямым ААо и АоА'. Аналогично

построены тени остальных точек.

Перечисленные в начале параграфа

свойства перспективно-аффинного соот-

ветствия присущи и ряду других точечных

преобразований. Назовем те из них, кото-

рые понадобятся в дальнейшем.

Параллельный перенос, определяемый

ненулевым вектором а. Известно, что па-

раллельный перенос (вектор) задается па-

рой соответствующих точек.

Так, вектор а(рис. 14) отображает лю-

бую точку А в точку А', расположенную

на луче заданного направления с нача-

лом в точке А на расстоянии |а|от этого

начала:

АА' = а .

Параллельный перенос фигуры Ф мож-

но определить как перемещение фигуры

в заданном направлении (см. рис. 14).

Фигура Ф', получающаяся из Ф парал-

лельным переносом на вектор а, равна фи-

гуре Ф.

Преобразования, основанные на парал-

лельном переносе, будут использованы при

конструировании поверхностей.

Осевая симметрия относительно данной

прямой т.

Это преобразование, которое каждую

точку А плоскости переводит в точку А',

так, что АА'±т и АА

= АоА' (А

е>4Л', Лоет). Можно показать, что осе-

вая симметрия является частным случаем

сжатия (растяжения).

Сжатие к прямой т.

Пусть на плоскости П задана прямая

т и указано некоторое число k, которое

Л',

А,

X',

т А

•N

К<1

К>1

о А'А

til

К—1 К'1

А'

Рис. 15

может быть и положительным, и отрица-

тельным.

Правила, позволяющие построить точку

А', соответствующую данной точке А, со-

стоят в следующем:

1. Точки А и А' должны лежать на

одном перпендикуляре к прямой m по одну

сторону от нее при k>0 и по разные

стороны, если k<0.

2. Расстояние

от точки

до прямой m из-

меняется в k раз,

т.

е. A'Ao = k-AoA (рис.

15).

Сжатие происходит при /г<1, когда

точки плоскости, кроме точек прямой т,

приближаются по перпендикулярам к пря-

мой т. Если /г>1, то все точки плоскости

удаляются от прямой — деформацией

плоскости будет растяжение.

Рис.

131

Рис.

132

Рис. 133

Сжатие к прямой при k= —

представ-

ляет собой осевую симметрию. Наконец,

если k=\, каждая точка плоскости пе-

реходит сама в себя, т. е. является непод-

вижной. Такое преобразование плоскости

является тождественным отображением

плоскости в себя.

Сжатию и растяжению можно подвер-

гать не только плоскость, но и простран-

ство.

В этом случае неподвижными окажутся

точки не прямой, а некоторой плоскости.

Такими точками при деформации сферы

Ф могут быть точки большого круга, плос-

кость которого перпендикулярна направ-

лению сжатия или растяжения (рис. 16).

Сфера Ф при таком преобразовании пе-

реходит в эллипсоид вращения Ф'.

При решении некоторых позиционных

задач на поверхности эллипсоида враще-

ния бывает целосообразно эту поверхность

подвергнуть сжатию, в результате которо-

го эллипсоид преобразуется в сферу. Та-

кое преобразование существенно упроща-

ет, например, решение задачи определения

точек пересечения прямой с эллипсоидом.

Мы познакомили читателя лишь с неко-

торыми положениями проективной геомет-

рии. Более подробные сведения о геомет-

рических преобразованиях и закономерно-

стях перспективной коллинеации можно

найти в специальной литературе [21].

РАЗДЕЛ 1

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ

ГЛАВА 2

ПРОЕКЦИИ точки

f 4. ОРТОГОНАЛЬНАЯ СИСТЕМА

ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Сущность метода ортогонального прое-

цирования заключается в том, что предмет

проецируется на две взаимно перпендику-

лярные плоскости лучами, ортогональны-

ми (перпендикулярными) к этим плоско-

стям.

Одну из плоскостей проекций П| распо-

лагают горизонтально, а вторую ГЬ —

вертикально (рис. 17). Плоскость Ш назы-

вают горизонтальной плоскостью проек-

ций, Пг — фронтальной. Плоскости П|

и Пг бесконечны и непрозрачны. Линия

пересечения плоскостей проекций называ-

ется осью координат и обозначается

Х|

. Плоскости проекций делят пространст-

во на четыре двугранных угла — четверти,

нумерация которых дана на рис. 17.

Рассматривая ортогональные проекции,

предполагают, что наблюдатель находится

в первой четверти на бесконечно большом

расстоянии от плоскостей проекций. Так

как эти плоскости непрозрачны, то види-

мыми для наблюдателя будут только те

точки, линии и фигуры, которые располо-

жены в пределах той же первой четверти.

При построении проекций необходимо по-

мнить, что ортогональной проекцией точки

на плоскость называется основание пер-

пендикуляра, опущенного из данной точки

на эту плоскость.

На

рис. 17 показаны точка А и ее орто-

гональные проекции А\ и At.

Точку Ai называют горизонталь-

ной проекцией точки А, точку Л

— ее

фронтальной проекцией. Каждая

из них является основанием перпендику-

ляра, опущенного из точки А соответ-

ственно на плоскости П| и Пг.

Можно доказать, что проекции точки

всегда расположены на прямых, перпенди-

кулярных оси Xi2 и пересекающих эту ось

в одной и той же точке. Действительно,

проецирующие лучи AAi и ААч определя-

ют плоскость, перпендикулярную плоско-

стям проекций и линии их пересечения —

оси xi

. Эта плоскость пересекает П| и Пг

по прямым А\А

и А

, которые образуют

с осью Xi2 и друг с другом прямые углы

с вершиной в точке А,.

Справедливо и обратное, т. е. если на

плоскостях проекций даны точки Ai и А%,

расположенные на прямых, пересекающих

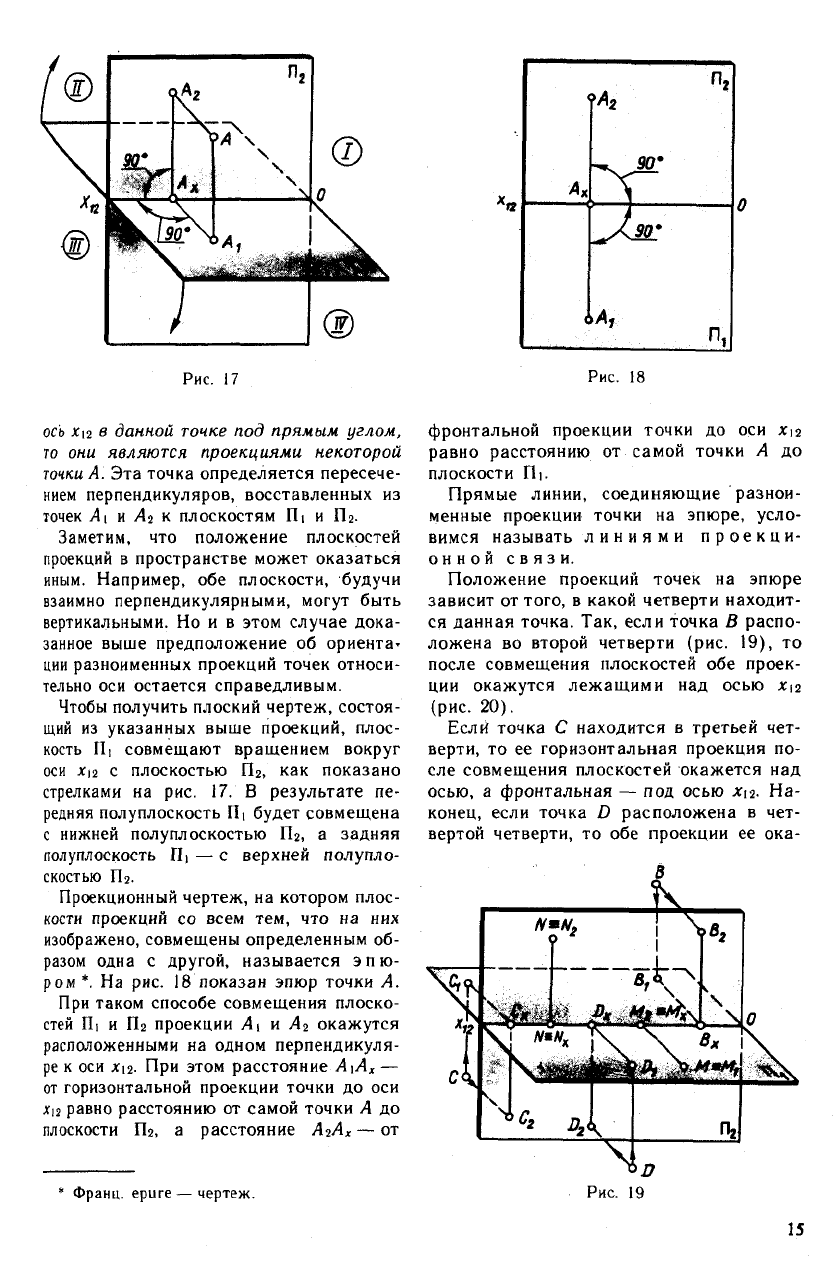
ось

Х\2

в данной точке под прямым углом,

то они являются проекциями некоторой

точки

А. Эта точка определяется пересече-

нием перпендикуляров, восставленных из

точек А\ и А? к плоскостям П| и Пг.

Заметим, что положение плоскостей

проекций в пространстве может оказаться

иным. Например, обе плоскости, будучи

взаимно перпендикулярными, могут быть

вертикальными. Но и в этом случае дока-

занное выше предположение об ориента-

ции разноименных проекций точек относи-

тельно оси остается справедливым.

Чтобы получить плоский чертеж, состоя-

щий из указанных выше проекций, плос-

кость П| совмещают вращением вокруг

оси *|2 с плоскостью Пг, как показано

стрелками на рис. 17. В результате пе-

редняя полуплоскость Hi будет совмещена

с нижней полуплоскостью Пг, а задняя

полуплоскость Hi — с верхней полупло-

скостью Пг.

Проекционный чертеж, на котором плос-

кости проекций со всем тем, что на них

изображено, совмещены определенным об-

разом одна с другой, называется эпю-

ром*. На рис. 18 показан эпюр точки А.

При таком способе совмещения плоско-

стей П1 и Пг проекции At и Лг окажутся

расположенными на одном перпендикуля-

ре к оси Xi2. При этом расстояние А\А

—

от горизонтальной проекции точки до оси

хи равно расстоянию от самой точки А до

плоскости Пг, а расстояние ЛгЛ* — от

* Франц. epure—чертеж.

•Л»

М*

Л,

Рис. 18

фронтальной проекции точки до оси Х12

равно расстоянию от самой точки А до

плоскости П|.

Прямые линии, соединяющие разнои-

менные проекции точки на эпюре, усло-

вимся называть линиями проекци-

онной связи.

Положение проекций точек на эпюре

зависит от того, в какой четверти находит-

ся данная точка. Так, если точка В распо-

ложена во второй четверти (рис. 19), то

после совмещения плоскостей обе проек-

ции окажутся лежащими над осью Х12

(рис. 20).

Еслй точка С находится в третьей чет-

верти, то ее горизонтальная проекция по-

сле совмещения плоскостей окажется над

осью, а фронтальная — под осью хц. На-

конец, если точка D расположена в чет-

вертой четверти, то обе проекции ее ока-

NmN,

9 в

<tB,

о D

Рис. 20

жутся под осью х12. На рис. 19 и 20 пока-

заны точки М и N, лежащие на плоскостях

проекций *. При таком положении точка

совпадает с одной из своих проекций, дру-

гая же проекция ее оказывается лежа-

щей на оси Xi2. Эта особенность отражена

и в обозначении: около той проекции, с ко-

торой совпадает сама точка, пишется за-

главная буква без индекса.

Следует отметить и тот случай, когда

обе проекции точки совпадают. Так будет,

если точка находится во второй или чет-

вертой четверти на одинаковом расстоя-

нии от плоскостей проекций. Обе проекции

совмещаются с самой точкой, если послед-

няя расположена на оси х^.

§ 5. ОРТОГОНАЛЬНАЯ СИСТЕМА

ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Выше было показано, что две проекции

точки определяют ее положение в про-

странстве. Так как каждая фигура или

тело представляет собой совокупность то-

чек, то можно утверждать, что и две орто-

гональные проекции предмета (при нали-

чии буквенных обозначений) вполне опре-

деляют его форму.

Однако в практике изображения строи-

тельных конструкций, машин и различных

инженерных сооружений возникает необ-

ходимость в создании дополнительных

проекций. Поступают так с единственной

целью — сделать проекционный чертеж

более ясным, удобочитаемым.

Модель трех плоскостей проекций пока-

зана на рис. 21. Третья плоскость, перпен-

* На рис. 19, 20 и последующих совпадаю-

щие точки соединены знаком тождества.

Рис. 21

дикулярная и Г1|, и Пг, обозначается бук-

вой Пз и называется профильной.

Проекции точек на эту плоскость будут

также именоваться профильными, а обоз-

начают их заглавными буквами или циф-

рами с индексом 3 (Л

, йз, Сз, ... 1з, 2

Зз...).

Плоскости проекций, попарно пересека-

ясь, определяют три оси: Ох, Оу и Ог,

которые можно рассматривать как систе-

му прямоугольных декартовых координат

в пространстве с началом в точке О. Сис-

тема знаков, указанная на рис. 22, со-

ответствует «правой системе» координат.

Три плоскости проекций делят про-

странство на восемь трехгранных углов —

это так называемые октанты. Нумера-

ция октантов дана на рис. 21.

Как и прежде, будем считать, что зри-

тель, рассматривающий предмет, находит-

ся в первом октанте.

Для получения эпюра плоскости П1 и Пз

вращают, как показано на рис. 21, до

совмещения с плоскостью Пг- В результа-

те вращения передняя полуплоскость П1

оказывается совмещенной с нижней по-

луплоскостью Пг, а задняя полуплоскость

П)—с верхней полуплоскостью Пг. При

повороте на 90° вокруг оси Ог передняя

полуплоскость Пз совместится с правой

полуплоскостью Пг, а задняя полупло-

скость Пз — с левой полуплоскостью Пг.

Окончательный вид всех совмещенных

плрскостей проекций дан на .рис. 22. На

этом чертеже оси Ох и Ог, лежащие в не-

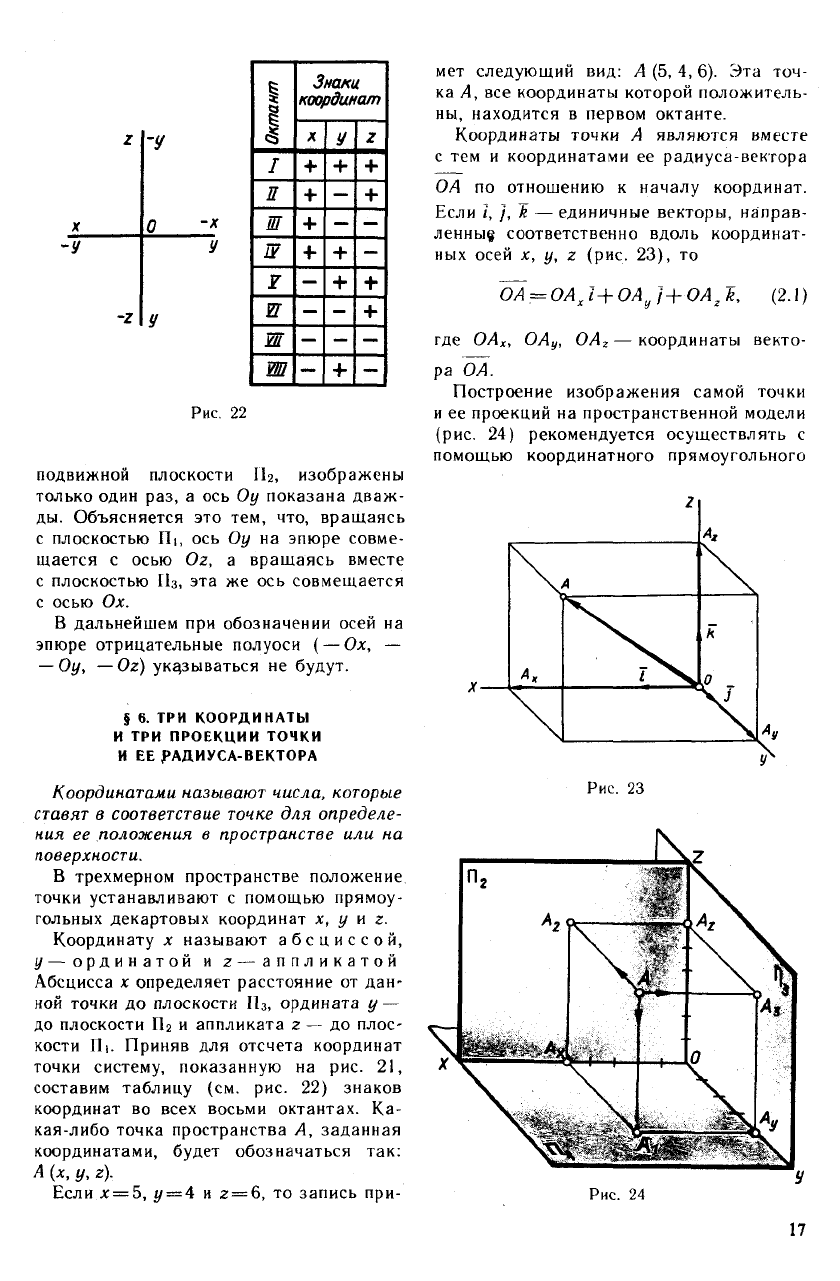
-У

-z

Октант

Знаки

координат

Октант

—

Ш +

—

+ +

—

— -

— — —

—

Рис.

подвижной плоскости

Пг,

изображены

только один

раз, а ось Оу

показана дваж-

ды. Объясняется

это тем, что,

вращаясь

с плоскостью

Hi, ось Оу на

эпюре совме-

щается

осью

Oz, а

вращаясь вместе

с плоскостью

Из, эта же ось

совмещается

с осью

Ох.

В дальнейшем

при

обозначении осей

на

эпюре отрицательные полуоси

(— Ох, —

—

Оу, —Oz)

указываться

не

будут.

6. ТРИ

КООРДИНАТЫ

ТРИ

ПРОЕКЦИИ точки

ЕЕ

РАДИ УСА-ВЕКТОРА

Координатами называют числа, которые

ставят

соответствие

точке

для

определе-

ния

ее

положения

пространстве

или на

поверхности.

В трехмерном пространстве положение

точки устанавливают

помощью прямоу-

гольных декартовых координат

х, у и г.

Координату

называют абсциссой,

—

ординатой

и z—

аппликатой

Абсцисса

определяет расстояние

от дан-

ной точки

до

плоскости

Пз,

ордината

у —

до плоскости

Пг и

аппликата

z — до

плос-

кости

П|.

Приняв

для

отсчета координат

точки систему, показанную

на рис. 21,

составим таблицу

(см. рис. 22)

знаков

координат

во

всех восьми октантах.

Ка-

кая-либо точка пространства

А,

заданная

координатами, будет обозначаться

так:

(х, у, г).

Если

х =

—А

то

запись

при-

мет следующий

вид: А (5, 4, 6). Эта точ-

ка

А, все

координаты которой положитель-

ны, находится

первом октанте.

Координаты точки

являются вместе

тем и

координатами

ее

радиуса-вектора

по

отношению

началу координат.

Если

i, j, k —

единичные векторы, налрав-

ленны§ соответственно вдоль координат-

ных осей

х, у, z (рис. 23), то

ОА

—

ОА

!+ОА

]-\-ОА

1г,

(2.1)

где

ОА

, ОА

—

координаты векто-

ра

OA.

Построение изображения самой точки

ее

проекций

на

пространственной модели

(рис.

24)

рекомендуется осуществлять

помощью координатного прямоугольного

Рис.

параллелепипеда. Прежде всего на осях

координат от точки О откладывают отрез-

ки, соответственно равные 5, 4 и 6 едини-

цам длины. На этих отрезках (ОЛ*, ОА

ОА

), как на ребрах, строят прямоуголь-

ный параллелепипед. Вершина его, проти-

воположная началу координат, и будет

определять заданную точку А. Легко заме-

тить, что для определения точки А доста-

точно построить только три ребра парал-

лелепипеда, например ОА

, А

Аi и AtA или

ОА

, А

А\ и А\ А и т. д. Эти ребра образу-

ют координатную ломаную линию, длина

каждого звена которой определяется со-

ответствующей координатой точки.

Однако построение параллелепипеда по-

зволяет определить не только точку А, но

и все три ее ортогональные проекции.

Лучами, проецирующими точку на плос-

кости Пь Пг и Пз, являются те три ребра

параллелепипеда, которые пересекаются

в точке А.

Каждая из ортогональных проекций

точки А, будучи расположенной на плоско-

сти, определяется только двумя координа-

тами.

Так, горизонтальная проекция А\ опре-

деляется координатами х и у, фронтальная

проекция Л

— координатами х и г, про-

фильная проекция Аз — координатами у и

г. Но две любые проекции определяются

тремя координатами. Вот почему задание

точки двумя проекциями равносильно за-

данию точки тремя координатами.

На эпюре (рис. 25), где все плоскости

проекций совмещены, проекции Л| и Аг

окажутся на одном перпендикуляре к оси

Ох, а проекции Аг и Аз — на одном пер-

пендикуляре к оси Ог.

Что касается проекций А\ и Аз, то и они

связаны прямыми А\А

и АзА

, перпенди-

кулярными оси Оу. Но так как эта ось на

эпюре занимает два положения, то отре-

зок AiAg не может быть продолжением

отрезка АзА

Построение проекций точки А (5, 4, 6) на

эпюре по заданным координатам выполня-

ют в такой последовательности: прежде

всего на оси абсцисс от начала координат

откладывают отрезок ОА

= х (в нашем

случае х = 5), затем через точку А

прово-

дят перпендикуляр к оси Ох, на котором

с учетом знаков откладываем отрезки

А\=у (получаем А\) и А

= г (полу-

чаем А2). Остается построить профильную

проекцию точки А

л.

Так как профильная

и фронтальная проекции точки должны

быть расположены на одном перпендику-

ляре к оси Ог, то через А

проводят пря-

мую A

Az-LOZ.

Наконец, возникает последний вопрос:

на каком расстоянии от оси Ог должна

находиться Аз?

Рассматривая координатный параллеле-

пипед (см. рис. 24), ребра которого

Аз = ОА

= А

=у, заключаем, что ис-

комое расстояние А

равно у. Отрезок

откладывают вправо от оси Ог, если

у>0, и влево, если у<с0.

Проследим за тем, какие изменения про-

изойдут на эпюре, когда точка начнет ме-

нять свое положение в пространстве.

Пусть, например, точка А (5, 4, 6) станет

перемещаться по прямой, перпендикуляр-

ной плоскости П

. При таком движении

будет меняться только одна координата у,

показывающая расстояние от точки до

плоскости Пг. Постоянными будут оста-

ваться координаты х и г, а проекция точ-

ки, определяемая этими координатами,

т. е. А2, не изменит своего положения.

Что касается проекций А\ и Л

, то пер-

вая начнет приближаться к оси Ох, вто-

рая — к оси Ог. На рис. 26 и 27 новому

положению точки соответствуют обозначе-

ния А

[

(А\,А\,Аз). В тот момент, когда

точка окажется на плоскости П

(у = 0),

две из трех проекций (Л? и Аз) будут

лежать на осях.

Переместившись из / октанта во //, точ-

ка начнет удаляться от плоскости П

, ко-

ордината у станет отрицательной, ее абсо-

лютная величина будет возрастать. Гори-

Рис. 131 Рис. 132 Рис. 133

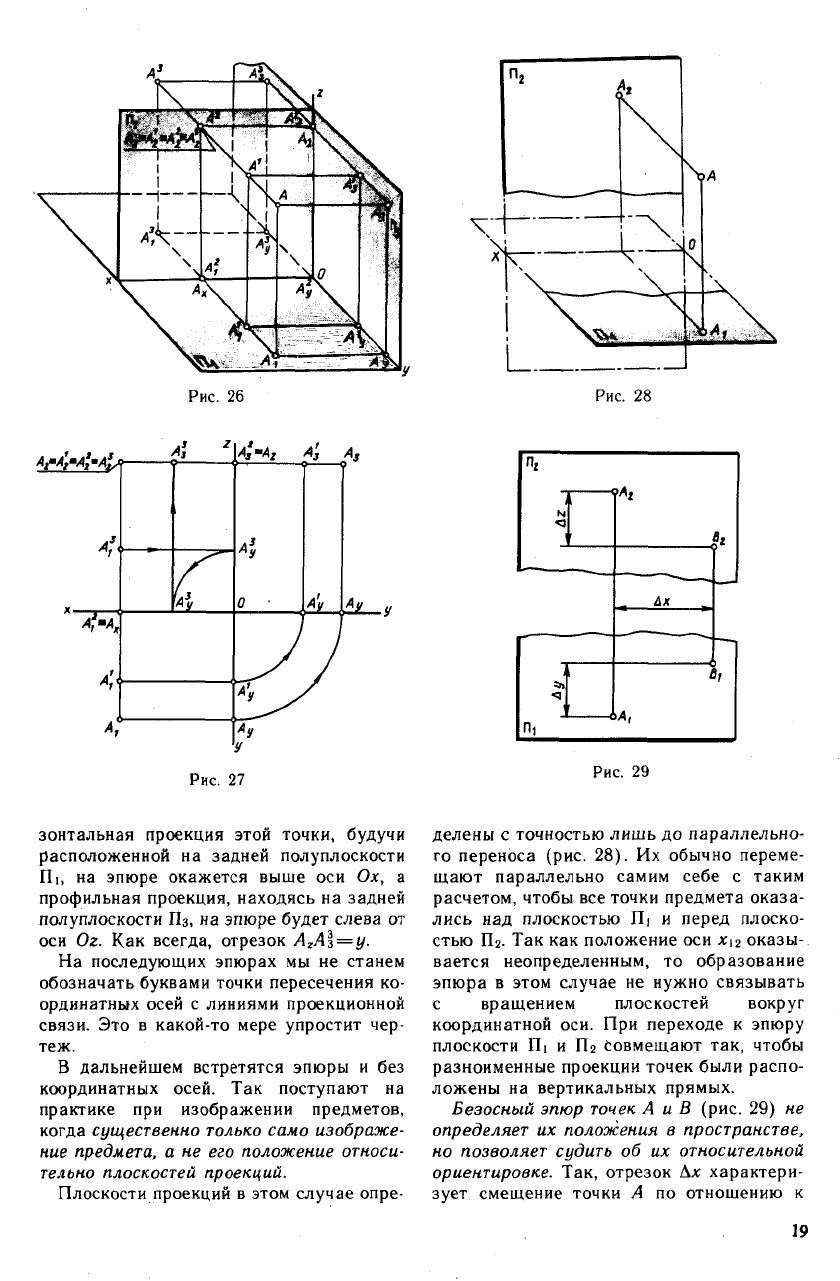
Рис. 26

Рис. 28

1 2

А1

а'

Рис. 27

«а

Ах

П)

-6А,

Рис. 29

зонтальная проекция этой точки, будучи

расположенной на задней полуплоскости

Пь на эпюре окажется выше оси Ох, а

профильная проекция, находясь на задней

полуплоскости Пз, на эпюре будет слева от

оси Oz. Как всегда, отрезок A

A\ = y.

На последующих эпюрах мы не станем

обозначать буквами точки пересечения ко-

ординатных осей с линиями проекционной

связи. Это в какой-то мере упростит чер-

теж.

В дальнейшем встретятся эпюры и без

координатных осей. Так поступают на

практике при изображении предметов,

когда существенно только само изображе-

ние предмета, а не его положение относи-

тельно плоскостей проекций.

Плоскости проекций в этом случае опре-

делены с точностью лишь до параллельно-

го переноса (рис. 28). Их обычно переме-

щают параллельно самим себе с таким

расчетом, чтобы все точки предмета оказа-

лись над плоскостью П| и перед плоско-

стью Щ. Так как положение оси x

оказы-

вается неопределенным, то образование

эпюра в этом случае не нужно связывать

с вращением плоскостей вокруг

координатной оси. При переходе к эпюру

плоскости П1 и П2 Совмещают так, чтобы

разноименные проекции точек были распо-

ложены на вертикальных прямых.

Безосный эпюр точек А и В (рис. 29) не

определяет их положения в пространстве,

но позволяет судить об их относительной

ориентировке. Так, отрезок Ах характери-

зует смещение точки А по отношению к