Крылов Н.Н., ред. Начертательная геометрия
Подождите немного. Документ загружается.


точке В в направлении, параллельном
плоскостям П| и Пг. Иными словами, Ах
указывает, насколько точка А расположе-
на левее точки В. Относительное смещение
точки в направлении, перпендикулярном
плоскости П
2
, определяется отрезком А у,
т. е. точка А в нашем примере ближе
к наблюдателю, чем точка В, на расстоя-
ние, равное А у.
Наконец, отрезок Аг показывает превы-
шение точки А над точкой В.
Сторонники безосного изучения курса
начертательной геометрии справедливо
указывают, что при решении многих задач
можно обходиться без осей координат.
Однако полный отказ от них нельзя при-
знать целесообразным. Начертательная
геометрия призвана подготовить будущего
инженера не только к грамотному выпол-
нению чертежей, но и к решению различ-
ных технических задач, среди которых не
последнее место занимают задачи про-
странственной статики и механики. А для
этого необходимо воспитывать умение
ориентировать тот или иной предмет отно-
сительно декартовых осей координат. Ука-
занные навыки будут необходимы и при
изучении таких разделов начертательной
геометрии, как перспектива и аксономет-
рия. Поэтому на ряде эпюров этой книги
мы сохраняем изображения координатных
осей. Такие чертежи определяют не только
форму предмета, но и его расположение
относительно плоскостей проекций.
Вопросы для самоконтроля
1. Какими координатами определяется каж-
дая проекция точки?
2. На границе каких октантов расположена
точка А (6, 0, —5)?
3. В каком октанте находится точка, если все
ее координаты отрицательны?
4. Какие координаты и проекции точки будут
изменяться, если точка перемещается в направ-
лении, перпендикулярном профильной плоско-
сти проекций Г1
3
? Параллельно оси г?
5. В каком случае проекция точки совпадает
с самой точкой? Где располагаются две другие
проекции этой точки?
6. Точки А и В расположены симметрично
относительно плоскости Пг. Какому условию
должны удовлетворять их координаты?
7. Что представляет собой множество точек
пространства, все три проекции каждой из кото-
рых оказываются совмещенными одна с другой?
ГЛАВА 3
ПРЯМАЯ ЛИНИЯ
§ 7. ЗАДАНИЕ ПРЯМОЙ ЛИНИИ
Прежде всего выясним вопрос: как
можно определить положение прямой в
пространстве?
Обычно отвечают: двумя точками. Это
верно, но не полно. Кроме двух точек
положение прямой можно определить дву-
мя плоскостями, двумя проекциями, точ-
кой и углами наклона к плоскостям про-
екций, точкой и направляющим вектором.
Не останавливаясь на первых двух спо-
собах задания прямой в пространстве, ко-
торые известны читателю из курса эле-
ментарной геометрии, покажем, что поло-
жение прямой вполне определяется дву-
мя ее проекциями.
Итак, пусть в плоскостях П1 и П
2
даны
две прямые: AiB
t
и А2В2 (рис. 30). Прове-
дем через эти прямые плоскости аир,
перпендикулярные плоскостям проекций.
В том случае, если эти плоскости не па-
раллельны, линией их пересечения будет
прямая ЛВ, проекциями которой являются
А\В\ и А2В2 (первая — горизонтальная
проекция, вторая—фронтальная).
Плоскости аир могут слиться в одну
плоскость у, если Л161 и А2В2 перпендику-
лярны оси х и пересекают ее в одной точке
(рис. 31).
Прямая линия в этом случае будет од-
нозначно определена своими проекциями,
если на каждой из них обозначить буква-
20

ми или цифрами две какие-либо точки.
Если же обозначений не сделать, то за
искомую прямую можно принять любую
прямую, лежащую в этой плоскости при
условии, что АВ%\ 1, и АВЩ
2
-
Существуют и аналитические способы
задания прямой в пространстве при помо-
щи уравнений.
Можно получить уравнение прямой в
векторной форме, если заданы радиус-
вектор г
А
(х
А
, у
А
, г
А
) одной из ее точек
(рис. 32) и направляющий вектор п
(Пх, Пу,
П
г
).
Для произвольной точки М прямой
справедливо следующее равенство:
?
м-~
г
А =
и
п> (
зл
)
где и — переменная величина, пробегаю-
щая все вещественные значения, называе-
мая параметром.
Векторному уравнению (3.1) прямой со-
ответствуют три скалярных:
х — х
А
= ип
х
,у — у
А
= ип
у
,
z — z
A
= un
z
, (3.2)
где х, у, z—координаты произвольной
точки прямой.
Векторное параметрическое уравнение
прямой будет не раз использовано при
составлении уравнений линейчатых повер-
хностей, формирование которых происхо-
дит при движении прямой линии.
Прямую линию можно задать и уравне-
ниями ее проекций в виде
A
i
x + B
l
y = C
i
\
А^х-\-В
2
г = С
ь
]
КЛ
'
Л)
где первое уравнение описывает горизон-
тальную проекцию прямой, а второе —
фронтальную. В том случае, когда прямая
задана двумя точками А (х
д
, у
А
, z
A
) и
В (х
в
, у
в
, z
B
), то уравнения (3.3) принима-
ют вид
Х
~
Х
А У-УА
Х
В
Х
A
Z
B
Z
A
Заметим, что каждому из уравнений
(3.3) или (3.4) соответствует плоскость,
перпендикулярная одной из плоскостей
проекций. Так, первые уравнения системы
(3.3) и (3.4) определяют плоскость a J.
И i
(см. рис. 30), а вторые — плоскость р±1Ь.
§ 8. РАЗЛИЧНЫЕ
ПОЛОЖЕНИЯ ПРЯМОЙ ЛИНИИ
ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
1. Прямой общего положения (см. рис.
30 *) называется прямая, не параллельная
ни одной из плоскостей проекций. На эпю-
ре (рис. 33) эта прямая задана проекция-
ми двух точек — А и В. Соединяя прямы-
ми одноименные проекции точек, получают
проекции отрезка прямой.
2. Прямые, параллельные горизонталь-
ной плоскости проекций (рис. 34 и 35),
* В данном и многих последующих примерах
каждая прямая на эпюре изображается в виде
отрезка прямой.
21
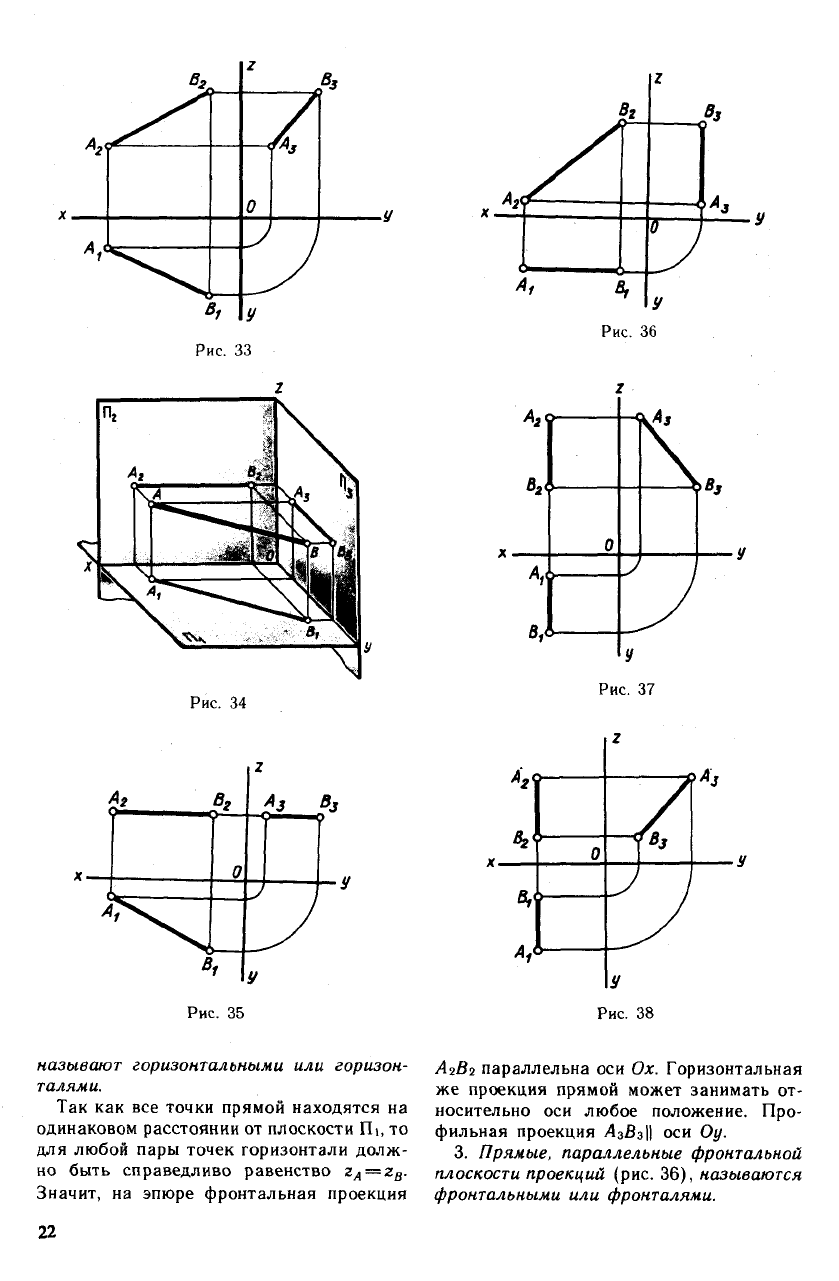
Рис. 33
г
Рис. 35
называют горизонтальными или горизон-
талями.
Так как все точки прямой находятся на
одинаковом расстоянии от плоскости Пь то
для любой пары точек горизонтали долж-
но быть справедливо равенство z
A
= z
B
.
Значит, на эпюре фронтальная проекция
z
А2В2 параллельна оси Ох. Горизонтальная
же проекция прямой может занимать от-
носительно оси любое положение. Про-
фильная проекция /4
3
Вз|] оси Оу.
3. Прямые, параллельные фронтальной
плоскости проекций (рис. 36), называются
фронтальными или фронталями.
22
"г
с,
-В, El f*
в*
1
Л
,
>
щ
1
Л
,
>
щ
ff fl
6 С,
Рис. 39
Рассуждая, как в п. 2, убеждаемся, что
горизонтальная проекция фронтали па-
раллельна оси Ох, фронтальная в общем
случае занимает произвольное положение,
а профильная — параллельна оси Oz.
4. Прямые, параллельные профильной
плоскости проекций (рис. 37 и 38), назы-
ваются профильными. Для любых двух
точек профильной прямой справедливо ра-
венство х
А
—х
в
, а значит, горизонтальная
и фронтальная проекции этой прямой бу-
дут перпендикулярны оси Ох.
Различают восходящую и нисходящую
профильные прямые. Первая по мере, уда-
ления от зрителя поднимается, вторая —
понижается. На рис. 37 представлен отре-
зок восходящей профильной прямой, на
рис. 38 — отрезок нисходящей прямой.
Прямые, параллельные плоскостям про-
екций, называются прямыми уровня.
Каждая из них проецируется на парал-
лельную ей плоскость без искажения.
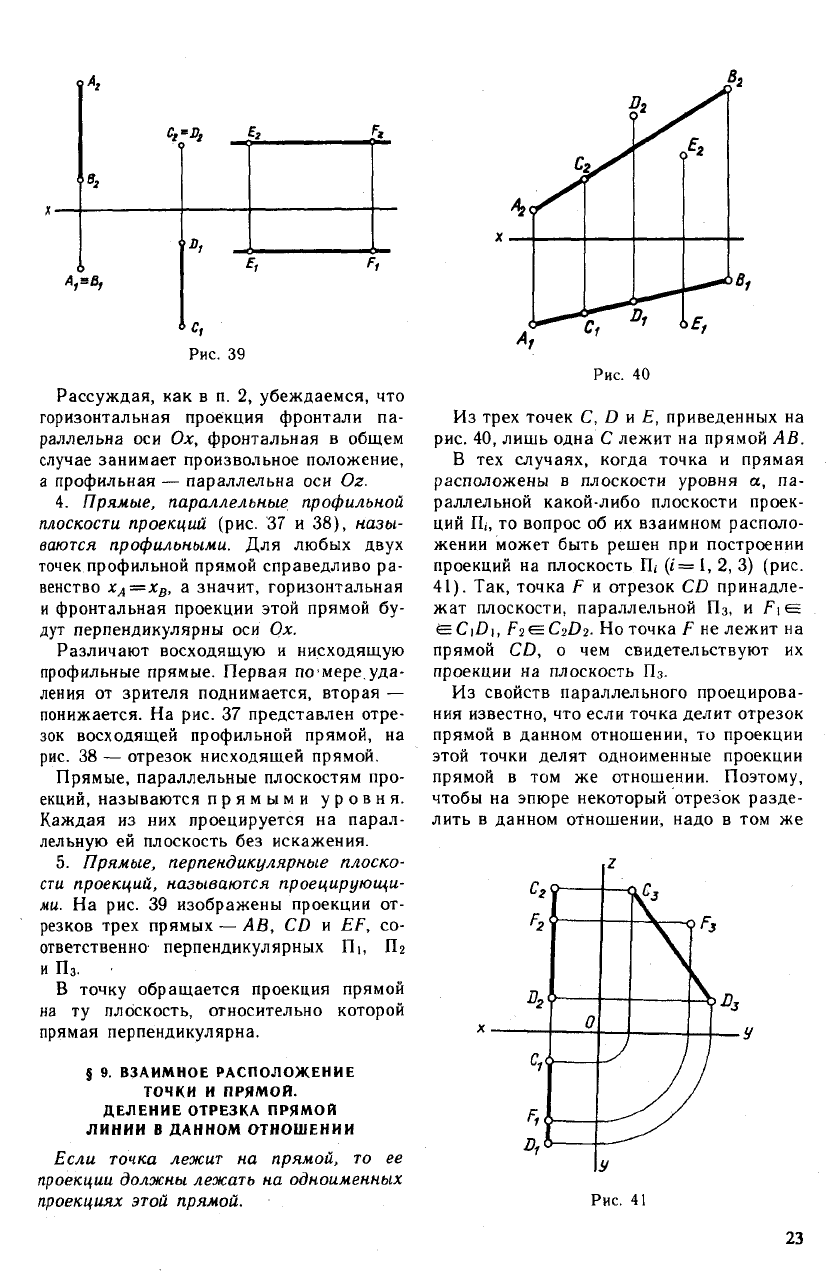
5. Прямые, перпендикулярные плоско-
сти проекций, называются проецирующи-
ми. На рис. 39 изображены проекции от-
резков трех прямых — АВ, CD и EF, со-
ответственно перпендикулярных Пь Пг
и П
3
.
В точку обращается проекция прямой
на ту плоскость, относительно которой
прямая перпендикулярна.
§ 9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧКИ И ПРЯМОЙ.
ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ
ЛИНИИ В ДАННОМ ОТНОШЕНИИ
Если точка лежит на прямой, то ее
проекции должны лежать на одноименных
проекциях этой прямой.
Из трех точек С, D и Е, приведенных на
рис. 40, лишь одна С лежит на прямой АВ.
В тех случаях, когда точка и прямая
расположены в плоскости уровня а, па-
раллельной какой-либо плоскости проек-
ций П,, то вопрос об их взаимном располо-
жении может быть решен при построении
проекций на плоскость П, (t= 1, 2, 3) (рис.
41). Так, точка F и отрезок CD принадле-
жат плоскости, параллельной П
3
, и F\ е
eCiDi, ГгеСг/Эг- Но точка F не лежит на
прямой CD, о чем свидетельствуют их
проекции на плоскость Щ.
Из свойств параллельного проецирова-
ния известно, что если точка делит отрезок
прямой в данном отношении, то проекции
этой точки делят одноименные проекции
прямой в том же отношении. Поэтому,
чтобы на эпюре некоторый отрезок разде-
лить в данном отношении, надо в том же
23
отношении разделить его проекции. На
рис. 40 отрезок АВ разделен точкой С в от-
ношении АС:СВ—\:3.
Возвращаясь к рис. 41, можно сделать
вывод (без построения третьей проекции),
что точка F не принадлежит прямой CD,
так как
C
2
f 2 C
X
F |
§ 10. ОПРЕДЕЛЕНИЕ
ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ЛИНИИ
И УГЛОВ НАКЛОНА ПРЯМОЙ
К ПЛОСКОСТИ ПРОЕКЦИЙ
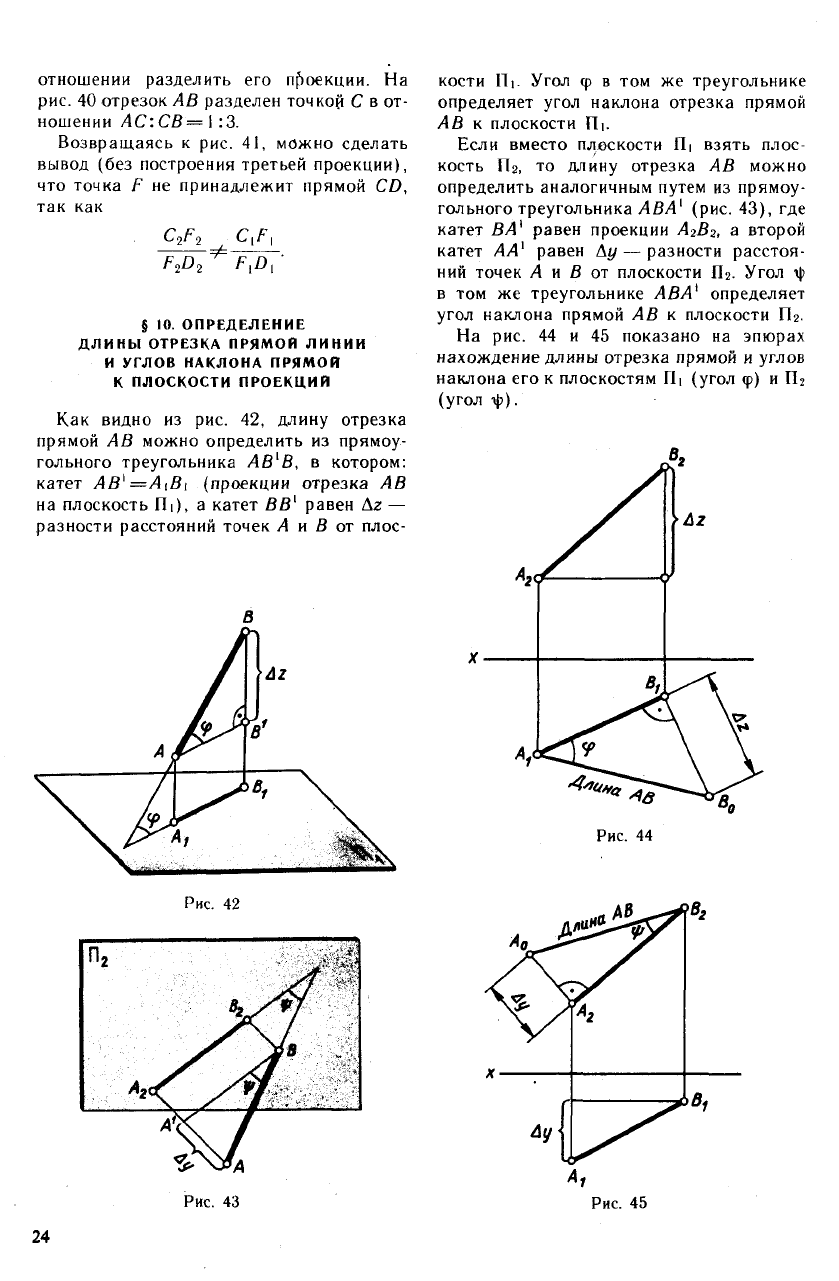
Как видно из рис. 42, длину отрезка
прямой АВ можно определить из прямоу-
гольного треугольника АВ
[
В, в котором:
катет АВ
1
=А tBi (проекции отрезка АВ
на плоскость П|), а катет ВВ
[
равен Az —
разности расстояний точек А и В от плос-
В
кости 111. Угол ср в том же треугольнике
определяет угол наклона отрезка прямой
АВ к плоскости Пь
Если вместо плоскости П| взять плос-
кость Пг, то длину отрезка АВ можно
определить аналогичным путем из прямоу-
гольного треугольника АВА
1
(рис. 43), где
катет ВА' равен проекции А
2
Вз, а второй
катет АА
1
равен Ду — разности расстоя-
ний точек А и В от плоскости П
2
. Угол г|>
в том же треугольнике ABA
1
определяет
угол наклона прямой АВ к плоскости Пг.
На рис. 44 и 45 показано на эпюрах
нахождение длины отрезка прямой и углов
наклона его к плоскостям Hi (угол ф) и Пг
(угол г|>).
Рис. 131 Рис. 132 Рис. 133
24

§ II. СЛЕДЫ ПРЯМОЙ ЛИНИИ
Следом прямой линии называется'точ-
ка,
в которой прямая пересекается с плос-
костью
проекций. Так как след прямой при-
надлежит одной из плоскостей проекций,
то одна из координат каждого следа дол-
жна быть равна нулю.
В общем случае прямая может пересе-
кать все три плоскости проекций и иметь
три следа:
горизонтальный след М—
точка пересечения прямой с плоскостью
III, ее координата г
л)
= 0;
фронтальный след N(y
N
= 0) —
точка пересечения прямой с плоско-
стью Пг;
профильный след Т(х
т
= 0)— пе-
ресечение с плоскостью Из.
Рассмотрим сначала прямую а в систе-
ме двух плоскостей проекций и найдем ее
горизонтальный и фронтальный следы.
Эти следы на рис. 46 определены как
точки, в которых прямая пересекается со
своими проекциями. Каждый след, явля-
ясь точкой, одновременно принадлежащей
и данной прямой и одной из плоскостей
проекций, совпадает с одноименной своей
проекцией. Так, М совпадает с Mi, а N —
с А/г. Что касается проекций, разноимен-
ных данному следу, то они расположены
на оси Ох, т. е. фронтальная проекция Л1г
горизонтального следа М и горизонталь-
ная проекция N\ следа N должны лежать
на оси Ох. Причем это будут те точки оси,
в которых она пересекается с соответству-
ющими проекциями данной прямой. Пе-
ресечение
а\
и оси Ох определяет N\, а пе-
ресечение аг и той же оси Ох дает Мг-
Отмеченные особенности в расположе-
нии проекций следов позволяют сформули-
ровать следующие правила построения
следов на эпюре:
1. Для построения горизонтального сле-
да М прямой необходимо продолжить ее
фронтальную проекцию до пересечения
с осью Ох и в этой точке восставить к оси
перпендикуляр до пересечения с горизон-
тальной проекцией прямой.
2. Для построения фронтального следа
N прямой нужно из точки пересечения
горизонтальной проекции ее с осью Ох
восставить перпендикуляр к оси до пересе-
чения с фронтальной проекцией прямой.
С помощью этих правил на рис. 47 и
48 найдены следы прямых а и Ь. Там же
показаны и совпавшие проекции точек А,
принадлежащих рассматриваемым пря-
мым. Особенность этих точек, как отмеча-
лось выше (см. § 4), заключается в том,
что они равноудалены от плоскостей про-
екций и тем самым находятся в биссектор-
ной плоскости р второй и четвертой чет-
вертей (Л = аПР). Если же некоторая пря-
мая а параллельна fS, то точка А становит-
ся несдбственной точкой прямой а. В этом
случае проекции ai и аг прямой а должны
быть параллельны.
25
Следы прямых, являясь точками, в кото-
рых прямая переходит из одной четверти
в другую, позволяют отмечать ее види-
мость. Видимой частью прямой будет та,
которая расположена в пределах первого
октанта. Проекции прямой, соответствую-
щие ее видимой части, изображаются
.сплошными линиями, а соответствующие
невидимым частям — штриховыми.
Рассмотрим построение следов прямой
линии в системе трех плоскостей проекций.
Горизонтальный и фронтальный следы
прямой определяются по тем правилам,
которые были указаны выше. Появится
только необходимость показать и про-
фильные проекции этих точек.
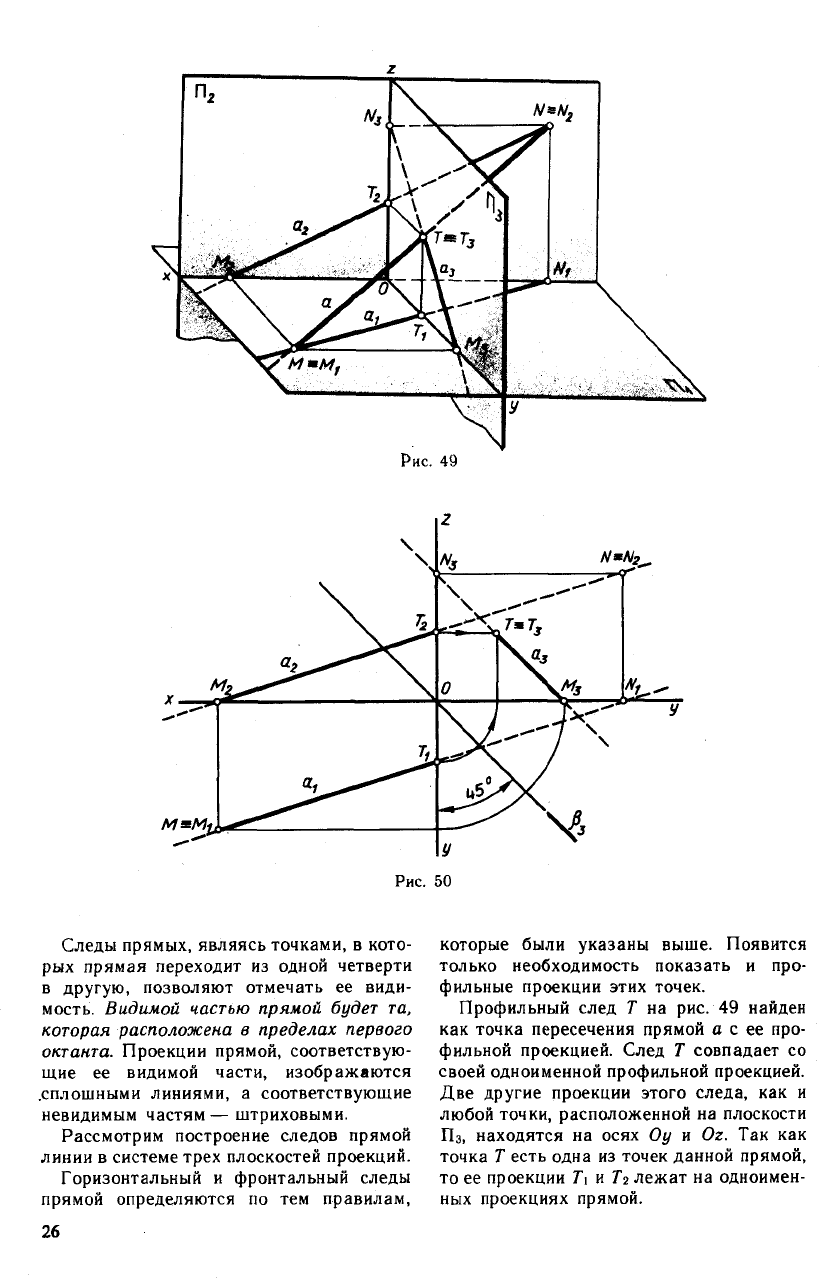
Профильный след Т на рис. 49 найден
как точка пересечения прямой а с ее про-
фильной проекцией. След Т совпадает со
своей одноименной профильной проекцией.
Две другие проекции этого следа, как и
любой точки, расположенной на плоскости
Пз, находятся на осях Оу и Ог. Так как
точка Т есть одна из точек данной прямой,
то ее проекции
Т\
и Тг лежат на одноимен-
ных проекциях прямой.
26
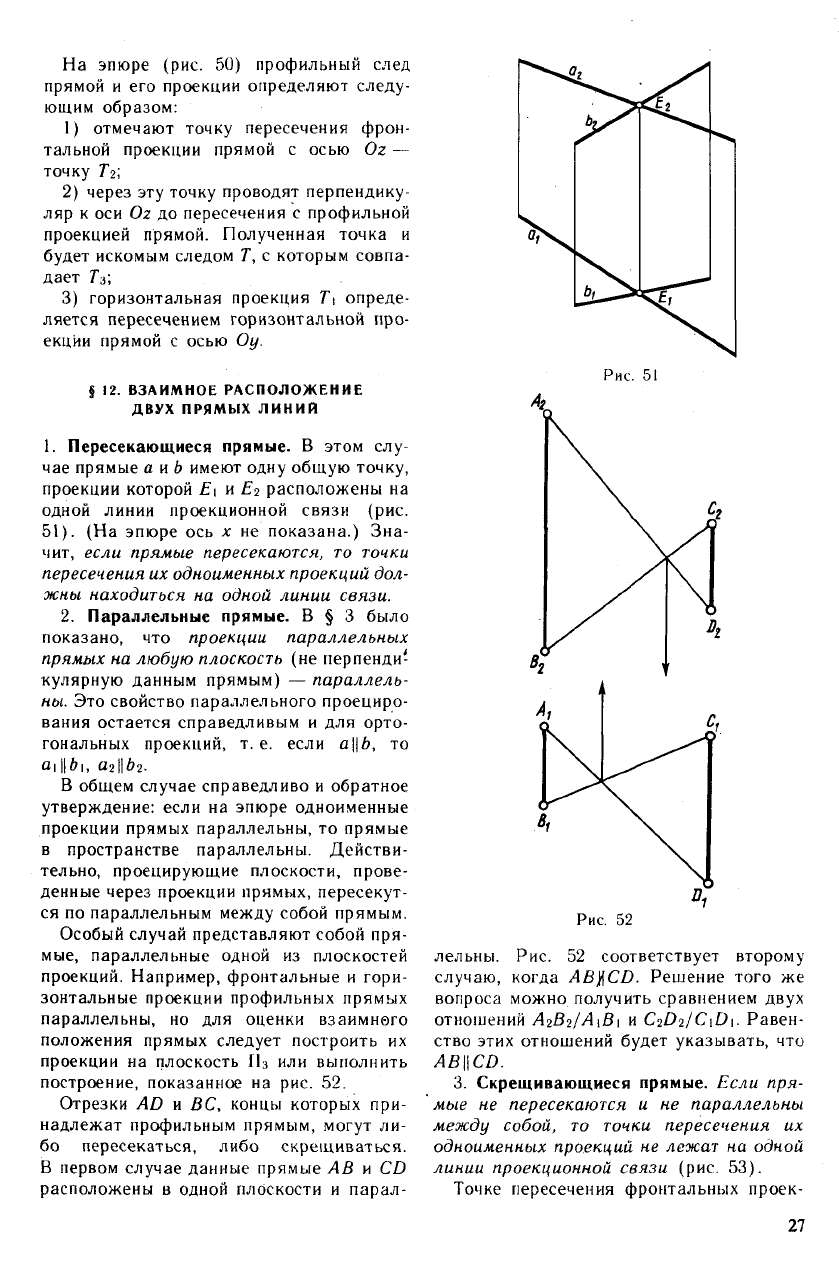
На эпюре (рис. 50) профильный след
прямой и его проекции определяют следу-
ющим образом:
1) отмечают точку пересечения фрон-
тальной проекции прямой с осью Oz —
точку Гг;
2) через эту точку проводят перпендику-
ляр к оси Oz до пересечения с профильной
проекцией прямой. Полученная точка и
будет искомым следом Т, с которым совпа-
дает Г
3
;
3) горизонтальная проекция Т\ опреде-
ляется пересечением горизонтальной про-
екции прямой с осью Оу.
§ 12. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПРЯМЫХ ЛИНИЙ
1. Пересекающиеся прямые. В этом слу-
чае прямые а и b имеют одну общую точку,
проекции которой Е\ и Е
2
расположены на
одной линии проекционной связи (рис.
51). (На эпюре ось х не показана.) Зна-
чит, если прямые пересекаются, то точки
пересечения их одноименных проекций дол-
жны находиться на одной линии связи.
2. Параллельные прямые. В § 3 было
показано, что проекции параллельных
прямых на любую плоскость (не перпенди-
кулярную данным прямым) — параллель-
ны. Это свойство параллельного проециро-
вания остается справедливым и для орто-
гональных проекций, т. е. если а\\Ь, то
а,
||6|, а
2
\\Ьг-
В общем случае справедливо и обратное
утверждение: если на эпюре одноименные
проекции прямых параллельны, то прямые
в пространстве параллельны. Действи-
тельно, проецирующие плоскости, прове-
денные через проекции прямых, пересекут-
ся по параллельным между собой прямым.
Особый случай представляют собой пря-
мые, параллельные одной из плоскостей
проекций. Например, фронтальные и гори-
зонтальные проекции профильных прямых
параллельны, но для оценки взаимного
положения прямых следует построить их
проекции на плоскость Из или выполнить
построение, показанное на рис. 52.
Отрезки AD и ВС, концы которых при-
надлежат профильным прямым, могут ли-
бо пересекаться, либо скрещиваться.
В первом случае данные прямые АВ и CD
расположены в одной плоскости и парал-
лельны. Рис. 52 соответствует второму
случаю, когда AB%CD. Решение того же
вопроса можно получить сравнением двух
отношений А2В2/А1В1 и C2D2/C1D1. Равен-
ство этих отношений будет указывать, что
АВ\\
CD.
3. Скрещивающиеся прямые. Если пря-
мые не пересекаются и не параллельны
между собой, то точки пересечения их
одноименных проекций не лежат на одной
линии проекционной связи (рис. 53).
Точке пересечения фронтальных проек-
27

ций прямых соответствуют две точки £ и
F, из которых одна принадлежит прямой,а,
другая — прямой Ь. Их фронтальные про-
екции совпадают лишь потому, что в про-
странстве обе точки — Е и F — находятся
на общем перпендикуляре к плоскости Пг.
Горизонтальная проекция этого перпенди-
куляра, обозначенная стрелкой (рис. 53),
позволяет установить, какая из двух точек
ближе к зрителю*. В нашем случае ближе
к зрителю находится точка Е, лежащая на
прямой а. Следовательно, прямая а прохо-
дит в этом месте впереди прямой Ь.
Точке пересечения горизонтальных про-
екций соответствуют также две точки К и
L, расположенные на разных прямых. Со-
впадение их горизонтальных проекций
произошло потому, что обе точки в про-
странстве оказались на одном перпендику-
ляре к плоскости П|.
Отмеченная стрелкой (см. рис. 53)
фронтальная проекция этого перпендику-
ляра дает ответ на вопрос о том, какая из
двух точек выше.
Как видно из чертежа, точка К выше
точки L. Следовательно, прямая b прохо-
дит над прямой а.
§ 13. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
ПРЯМЫЕ ЛИНИИ
Если две прямые пересекаются под пря-
мым углом, то проекции их в общем случае
образуют угол, не равный 90°.
* Предполагается, что прямые расположены
между зрителем и плоскостью проекций.
Для того чтобы прямой угол проециро-
вался в истинную величину, необходимо
и достаточно, чтобы одна из его сторон
была параллельна, а другая не перпенди-
кулярна плоскости проекций.
Действительно, пусть сторона АВ пря-
мого угла ABC параллельна плоскости
Г1 ь
Требуется доказать, что проекция его:
угол /4ifiiCi=90° (рис. 54).
Прямая АВ перпендикулярна плоскости
а, так как АВ перпендикулярна двум пря-
мым этой плоскости ВС и ВВ\, проходя-
щим через точку В.
Прямая АВ и ее проекция А\В\
—г-две
параллельные прямые, а потому
А\В\
так-
же перпендикулярна плоскости а. Следо-
вательно, А\В\ перпендикулярна В\С\.
Докажем теперь, что если ортогональ-
ная проекция угла ABC на некоторую
плоскость П| является прямым углом и од-
на из сторон угла параллельна той же
плоскости, то угол ABC — прямой (рис.
54).
Прямая Л|б| перпендикулярна плоско-
сти а, так как образует прямые углы с
б|С] по условию и с ВВ\ по построению.
Но А\В\ параллельна АВ. Значит, и пря-
мая А В-La. Следовательно, угол между
АВ и ВС — прямой.
В
28
[Ч.
w
-» а)
Ai
б)
о а
г
А,
9 С£ 9
h
Ч
Рис. 56
На основании изложенного можно ут-
верждать, что углы, показанные на рис.
55, являются проекциями прямых углов.
У первого из них сторона а параллельна
плоскости П|, у второго — сторона f па-
раллельна плоскости' Г1
2
.
Вопросы и задачи для самоконтроля
1. Как расположена прямая I общего поло-
жения в пространстве, если /1Ц/2?
2. Как расположена прямая относительно
плоскостей проекций, если сумма углов, которые
она образует с
П i
и 1Ь, равна 90°?
3. Как на прямой линии определить точку,
равноудаленную от плоскостей Hi и Пг? На
какой прямой такой точки не существует?
4. Может ли ортогональная проекция острого
угла быть тупым углом, а тупого — острым?
5. Могут ли проекции скрещивающихся пря-
мых быть параллельными?
6. В каком случае проекции прямого угла на
плоскости III и Г1
2
равны 90°?
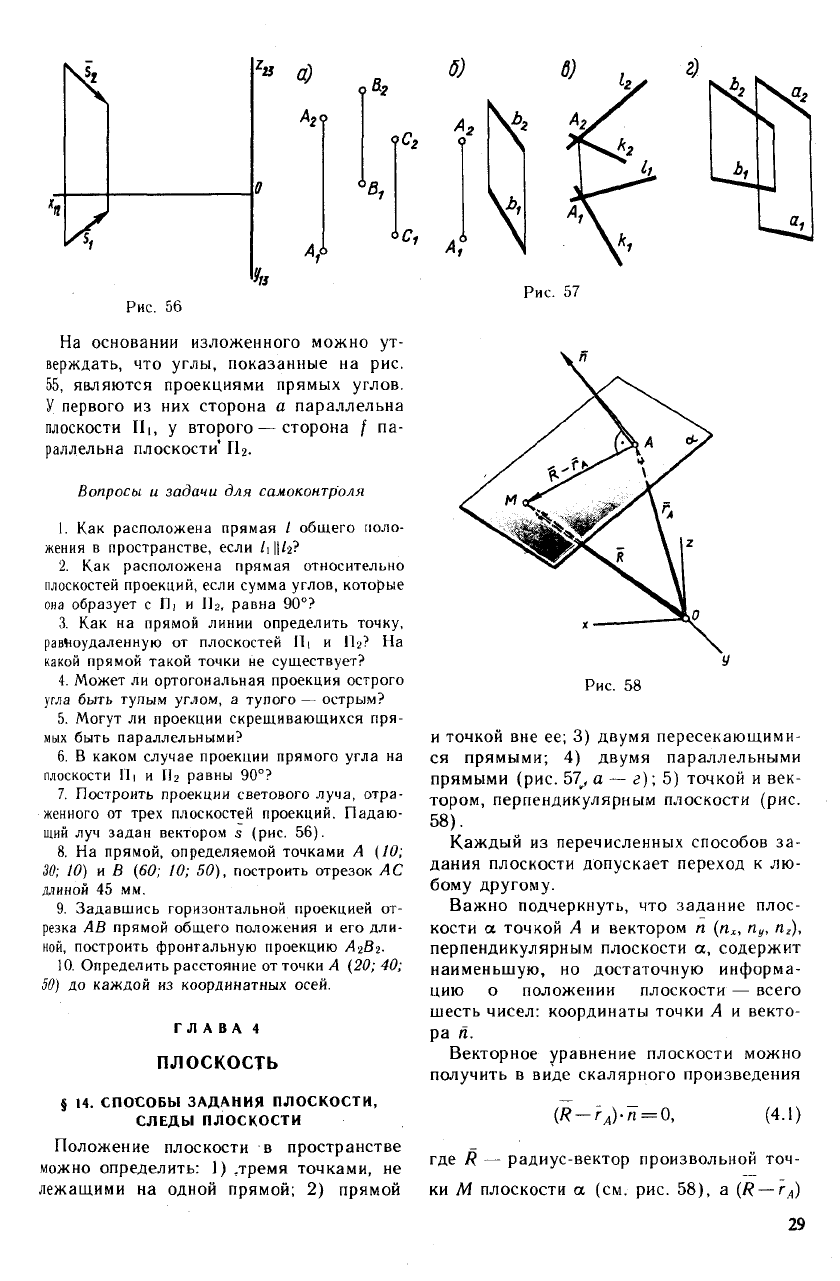
7. Построить проекции светового луча, отра-
женного от трех плоскостей проекций. Падаю-
щий луч задан вектором s (рис. 56).
8. На прямой, определяемой точками А (10;
30; 10) и В (60; 10; 50), построить отрезок АС
длиной 45 мм.
9. Задавшись горизонтальной проекцией от-
резка АВ прямой общего положения и его дли-
ной, построить фронтальную проекцию Л2В2.
10. Определить расстояние от точки А (20; 40;
50) до каждой из координатных осей.
ГЛАВА 4
плоскость
§ 14. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ,
СЛЕДЫ ПЛОСКОСТИ
Положение плоскости в пространстве
можно определить: 1) .тремя точками, не
лежащими на одной прямой; 2) прямой
Ч
к
г)
Рис. 57
Рис. 58
и точкой вне ее; 3) двумя пересекающими-
ся прямыми; 4) двумя параллельными
прямыми (рис. 57, а — г); 5) точкой и век-
тором, перпендикулярным плоскости (рис.
58).
Каждый из перечисленных способов за-
дания плоскости допускает переход к лю-
бому другому.
Важно подчеркнуть, что задание плос-
кости а точкой А и вектором п (п
х
, п
у
, п
2
),
перпендикулярным плоскости а, содержит
наименьшую, но достаточную информа-
цию о положении плоскости — всего
шесть чисел: координаты точки А и векто-
ра п.
Векторное уравнение плоскости можно
получить в виде скалярного произведения
(R-r
A
)-n = 0,
(4.1)
где R — радиус-вектор произвольной точ-
ки М плоскости а (см. рис. 58), a (R — г
А
)
29
