Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

Аг

Рис. 142

О вдоль той прямой, по которой перемеща-

ется горизонтальная проекция вершины А;

5) через полученную точку Л? и непод-

вижную DI проводим прямую до пересече-

ния с прямой, по которой перемещается

горизонтальная проекция вершины В;

6) соединяя найденные точки Л? и В\

друг с другом и с неподвижной вершиной

Сполучаем новую горизонтальную про-

екцию треугольника.

Эта проекция и определяет натуральную

величину Д ABC.

Фронтальная проекция треугольника

окажется преобразованной в прямую, ко-

торая совпадает с СгОг-

§ 33. СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО

ПЕРЕМЕЩЕНИЯ

Применение способа вращения часто

приводит к тому, что преобразованная

проекция фигуры накладывается на за-

данную. Построение и особенно чтение

такого чертежа при вращении трехмерных

фигур становится затруднительным.

Этого недостатка лишен способ плос-

копараллельного перемещения,

позволяющий более свободно пользовать-

ся полем чертежа для размещения пре-

образованных проекций геометрической

фигуры. Более свободно, но не произ-

вольно.

Ограничения, которым должны удовлет-

ворять вновь создаваемые проекции, обус-

ловлены понятием плоскопараллельного

движения. Так называют плоское движе-

ние геометрической фигуры, при котором

все ее точки движутся параллельно неко-

торой плоскости.

Из приведенного определения следует,

что вращательное движение фигуры явля-

ется частным случаем плоскопараллельно-

го, а способ вращения — частный случай

способа плоскопараллельного перемеще-

ния.

Причем нас должен интересовать только

результат движения, а не сам про-

цесс непрерывного изменения положения

фигуры в пространстве.

На эпюре перемещение осуществляют

параллельно плоскостям проекций (П| или

), когда каждая точка фигуры движется

в плоскостях уровня.

Каким же условиям должны удовлетво-

рять преобразованные проекции фигуры?

Рассмотрим плоскопараллельное пере-

мещение треугольника ABC относительно

плоскости П| (рис. 143).

Каждая из его вершин, двигаясь в плос-

костях уровня, опишет плоскую кривую,

фронтальная проекция которой будет со-

впадать с одноименным следом плоскости.

Это означает, что фронтальные проекции

вершин треугольника (точек любой фигу-

ры Ф) будут двигаться по прямым, пер-

пендикулярным линиям связи. Что же ка-

сается проекции треугольника на плос-

кость П|, то она может занять произволь-

ное положение, не изменив при этом своей

формы.

Рис. 131 Рис. 132 Рис. 133

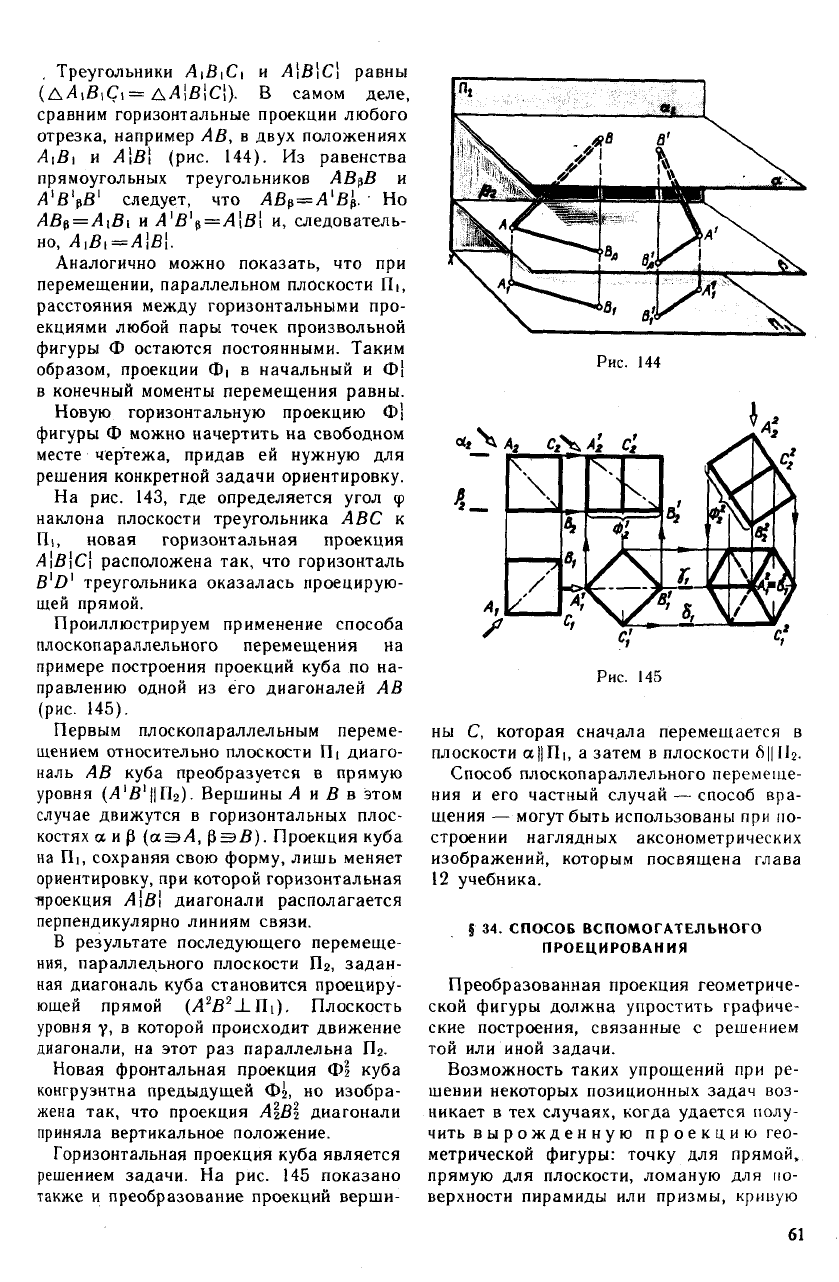
. Треугольники A\BiC\ и Л|В|С| равны

(АА\В\С\= АА\В\С[). В самом деле,

сравним горизонтальные проекции любого

отрезка, например АВ, в двух положениях

А\В\ и Л|В| (рис. 144). Из равенства

прямоугольных треугольников АВЦВ и

Л'В'цй' следует, что = Но

I = A

BI и А*В\ = А\В\ и, следователь-

но, А\В\ =Л !В|.

Аналогично можно показать, что при

перемещении, параллельном плоскости П|,

расстояния между горизонтальными про-

екциями любой пары точек произвольной

фигуры Ф остаются постоянными. Таким

образом, проекции Ф| в начальный и Ф|

в конечный моменты перемещения равны.

Новую горизонтальную проекцию Ф|

фигуры Ф можно начертить на свободном

месте чертежа, придав ей нужную для

решения конкретной задачи ориентировку.

На рис. 143, где определяется угол ф

наклона плоскости треугольника ABC к

П], новая горизонтальная проекция

А\В\С\ расположена так, что горизонталь

]

треугольника оказалась проецирую-

щей прямой.

Проиллюстрируем применение способа

плоскопараллельного перемещения на

примере построения проекций куба по на-

правлению одной из его диагоналей АВ

(рис. 145).

Первым плоскопараллельным переме-

щением относительно плоскости П| диаго-

наль АВ куба преобразуется в прямую

уровня (Л'б'ЦПг). Вершины Л и В в этом

случае движутся в горизонтальных плос-

костях аир (аэЛ, рэВ). Проекция куба

на Пь сохраняя свою форму, лишь меняет

ориентировку, при которой горизонтальная

проекция Л'В| диагонали располагается

перпендикулярно линиям связи.

В результате последующего перемеще-

ния, параллельного плоскости Пг, задан-

ная диагональ куба становится проециру-

ющей прямой (Л

_1_П1). Плоскость

уровня у, в которой происходит движение

диагонали, на этот раз параллельна П

Новая фронтальная проекция Ф1 куба

конгруэнтна предыдущей Ф

, но изобра-

жена так, что проекция Л1В| диагонали

приняла вертикальное положение.

Горизонтальная проекция куба является

решением задачи. На рис. 145 показано

также и преобразование проекций верши-

ны С, которая снач.ала перемещается в

плоскости а ЦП], а затем в плоскости ЙЦПг.

Способ плоскопараллельного перемеще-

ния и его частный случай — способ вра-

щения — могут быть использованы при по-

строении наглядных аксонометрических

изображений, которым посвящена глава

12 учебника.

f 34. СПОСОБ ВСПОМОГАТЕЛЬНОГО

ПРОЕЦИРОВАНИЯ

Преобразованная проекция геометриче-

ской фигуры должна упростить графиче-

ские построения, связанные с решением

той или иной задачи.

Возможность таких упрощений при ре-

шении некоторых позиционных задач воз-

никает в тех случаях, когда удается полу-

чить вырожденную проекцию гео-

метрической фигуры: точку для прямой,

прямую для плоскости, ломаную для по-

верхности пирамиды или призмы, кривую

для конической поверхности и цилиндри-

ческой.

Вырожденные проекции указанных гео-

метрических фигур получают вспомога-

тельным проецированием чаще

всего на одну из плоскостей проекции или

на плоскость уровня.

Это проецирование может быть и цен-

тральным, и параллельным (как прави-

ло, косоугольным).

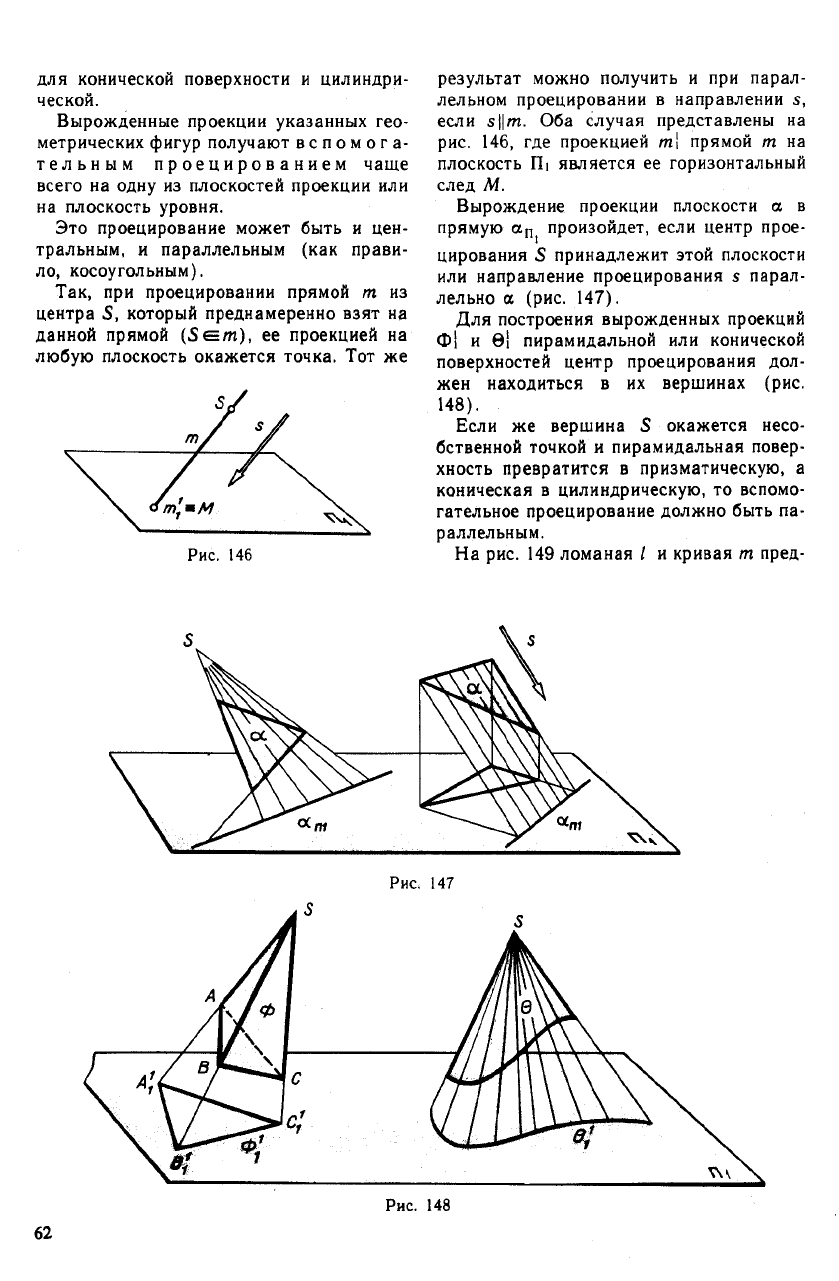
Так, при проецировании прямой т из

центра S, который преднамеренно взят на

данной прямой (Sen), ее проекцией на

любую плоскость окажется точка. Тот же

Рис. 146

результат можно получить и при парал-

лельном проецировании в направлении s,

если s\\m. Оба случая представлены на

рис. 146, где проекцией т\ прямой т на

плоскость П1 является ее горизонтальный

след М.

Вырождение проекции плоскости а в

прямую а

П|

произойдет, если центр прое-

цирования S принадлежит этой плоскости

или направление проецирования s парал-

лельно а (рис. 147).

Для построения вырожденных проекций

Ф| и в| пирамидальной или конической

поверхностей центр проецирования дол-

жен находиться в их вершинах (рис.

148).

Если же вершина 5 окажется несо-

бственной точкой и пирамидальная повер-

хность превратится в призматическую, а

коническая в цилиндрическую, то вспомо-

гательное проецирование должно быть па-

раллельным.

На рис. 149 ломаная I и кривая т пред-

Рис. 147

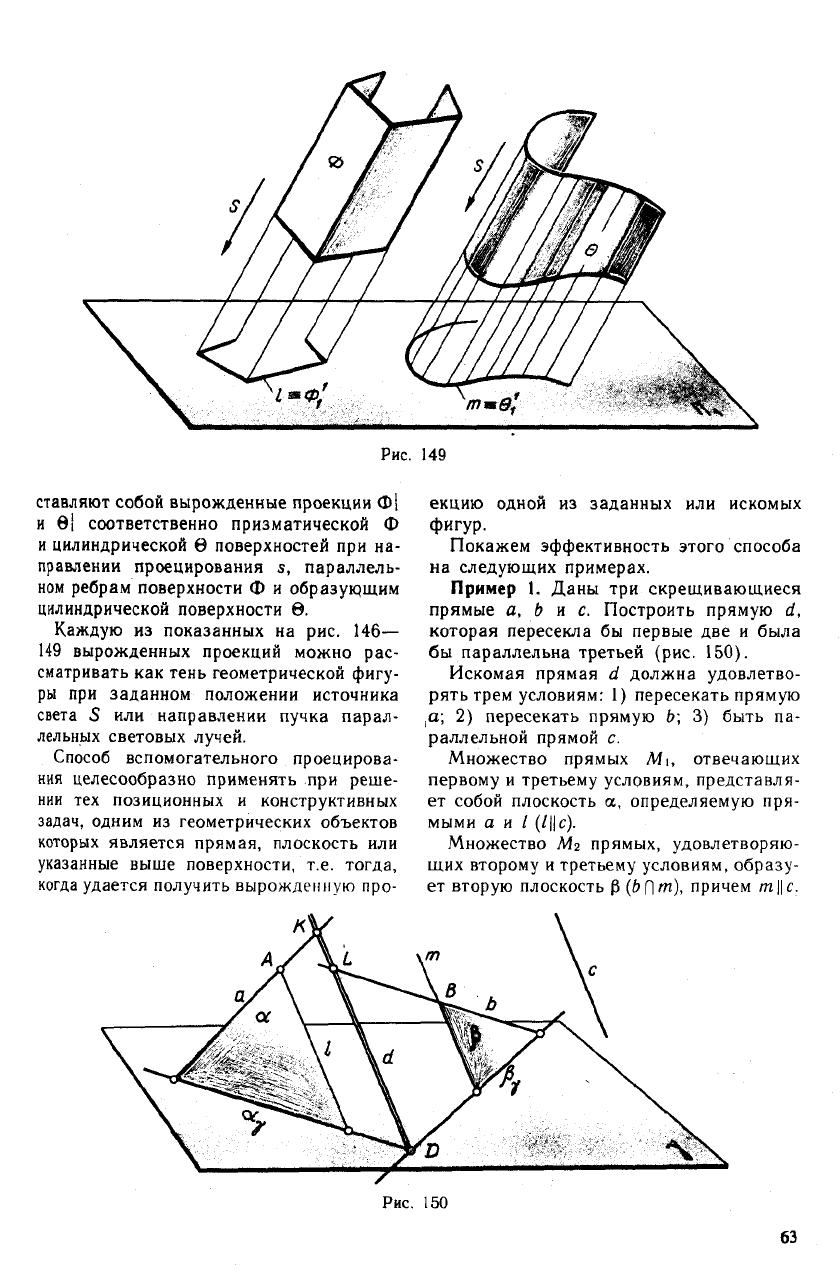
Рис. 149

ставляют собой вырожденные проекции Ф1

и в| соответственно призматической Ф

и цилиндрической 0 поверхностей при на-

правлении проецирования s, параллель-

ном ребрам поверхности Ф и образующим

цилиндрической поверхности в.

Каждую из показанных на рис. 146—

149 вырожденных проекций можно рас-

сматривать как тень геометрической фигу-

ры при заданном положении источника

света S или направлении пучка парал-

лельных световых лучей.

Способ вспомогательного проецирова-

ния целесообразно применять при реше-

нии тех позиционных и конструктивных

задач, одним из геометрических объектов

которых является прямая, плоскость или

указанные выше поверхности, т.е. тогда,

когда удается получить вырожденную про-

екцию одной из заданных или искомых

фигур.

Покажем эффективность этого способа

на следующих примерах.

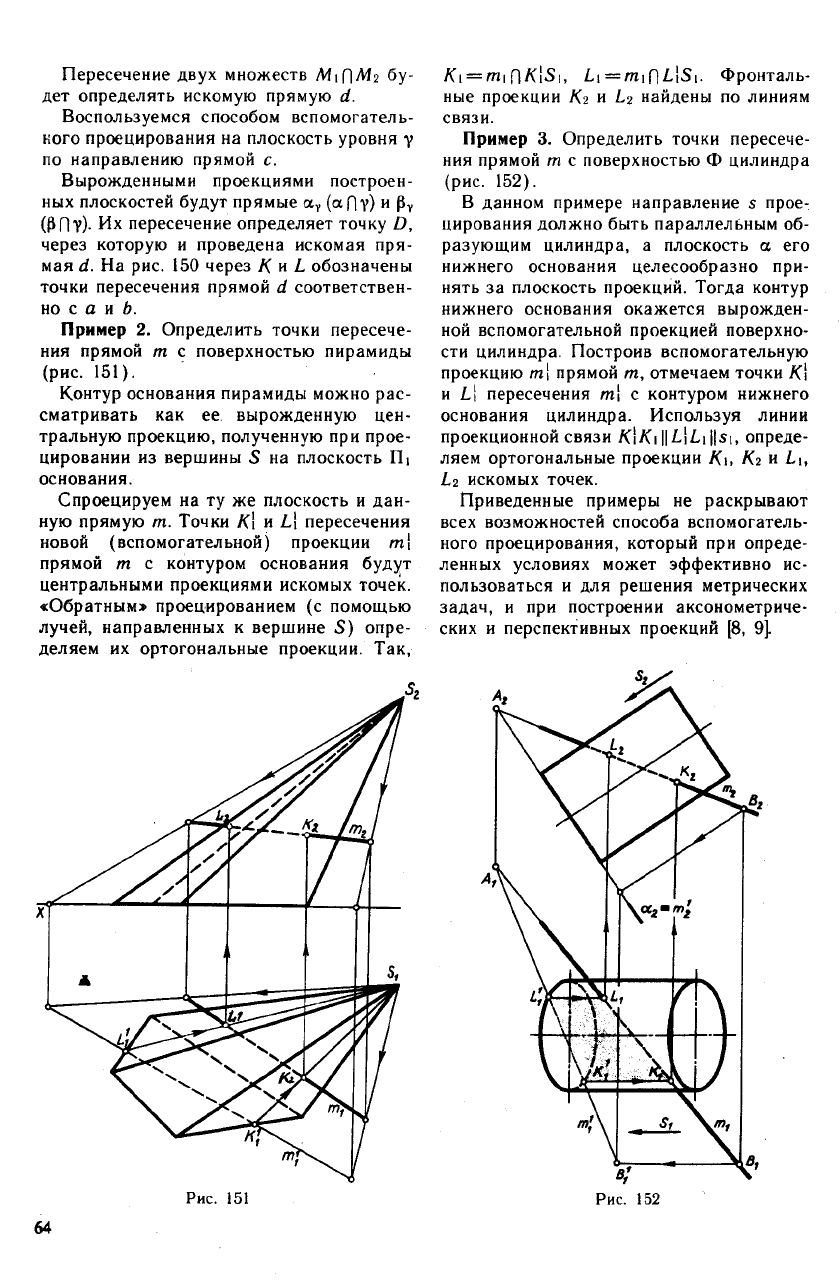
Пример 1. Даны три скрещивающиеся

прямые а, b и с. Построить прямую d,

которая пересекла бы первые две и была

бы параллельна третьей (рис. 150).

Искомая прямая d должна удовлетво-

рять трем условиям: 1) пересекать прямую

,а; 2) пересекать прямую 6; 3) быть па-

раллельной прямой с.

Множество прямых М\, отвечающих

первому и третьему условиям, представля-

ет собой плоскость а, определяемую пря-

мыми а и / (/||с).

Множество прямых, удовлетворяю-

щих второму и третьему условиям, образу-

ет вторую плоскость р (Ь[]т), причем т\\с.

Пересечение двух множеств М\[\Мг бу-

дет определять искомую прямую d.

Воспользуемся способом вспомогатель-

ного проецирования на плоскость уровня у

по направлению прямой с.

Вырожденными проекциями построен-

ных плоскостей будут прямые a

(aflv)

(РП?)- Их пересечение определяет точку D,

через которую и проведена искомая пря-

мая d. На рис. 150 через К и L обозначены

точки пересечения прямой d соответствен-

но с а и Ь.

Пример 2. Определить точки пересече-

ния прямой т с поверхностью пирамиды

(рис. 151).

Контур основания пирамиды можно рас-

сматривать как ее вырожденную цен-

тральную проекцию, полученную при прое-

цировании из вершины S на плоскость Ш

основания.

Спроецируем на ту же плоскость и дан-

ную прямую т. Точки К\ и L\ пересечения

новой (вспомогательной) проекции т

прямой т с контуром основания будут

центральными проекциями искомых точек.

«Обратным» проецированием (с помощью

лучей, направленных к вершине S) опре-

деляем их ортогональные проекции. Так,

^Ci

= mifl/C!Si, Z.i = miDi-iSi. Фронталь-

ные проекции К.2 и Z-2 найдены по линиям

связи.

Пример 3. Определить точки пересече-

ния прямой т с поверхностью Ф цилиндра

(рис. 152).

В данном примере направление s прое-

цирования должно быть параллельным об-

разующим цилиндра, а плоскость а его

нижнего основания целесообразно при-

нять за плоскость проекций. Тогда контур

нижнего основания окажется вырожден-

ной вспомогательной проекцией поверхно-

сти цилиндра. Построив вспомогательную

проекцию ml прямой т, отмечаем точки К\

и L\ пересечения т\ с контуром нижнего

основания цилиндра. Используя линии

проекционной связи /Ci/Ci ||L|Li||si, опреде-

ляем ортогональные проекции Ki, Кг и Li,

L2 искомых точек.

Приведенные примеры не раскрывают

всех возможностей способа вспомогатель-

ного проецирования, который при опреде-

ленных условиях может эффективно ис-

пользоваться и для решения метрических

задач, и при построении аксонометриче-

ских и перспективных проекций [8, 9J.

§ 35. ПРИМЕНЕНИЕ СПОСОБОВ

ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

К РЕШЕНИЮ МЕТРИЧЕСКИХ ЗАДАЧ

1. Определение расстояний

а) Расстояние между двумя точками.

Задача сводится к определению истинной

длины отрезка, соединяющего две данные

точки. Ее решение связано с преобразова-

нием чертежа, в результате которого дан-

ный отрезок оказывается параллельным

одной из плоскостей проекций (см. первую

из четырех основных задач, рассмотрен-

ных выше).

б) Расстояние от точки до прямой.

В § 28 было показано, что сложность ре-

шения этой задачи существенно зависит

от заданных проекций. Из трех случаев,

представленных на рис. 114—116, наибо-

лее простым был первый, когда прямая

I составляла с П| прямой угол и проециро-

валась на эту плоскость в точку.

Но к этому частному случаю расположе-

ния прямой I можно всегда прийти, ис-

пользуя построения, показанные выше при

решении второй основной задачи.

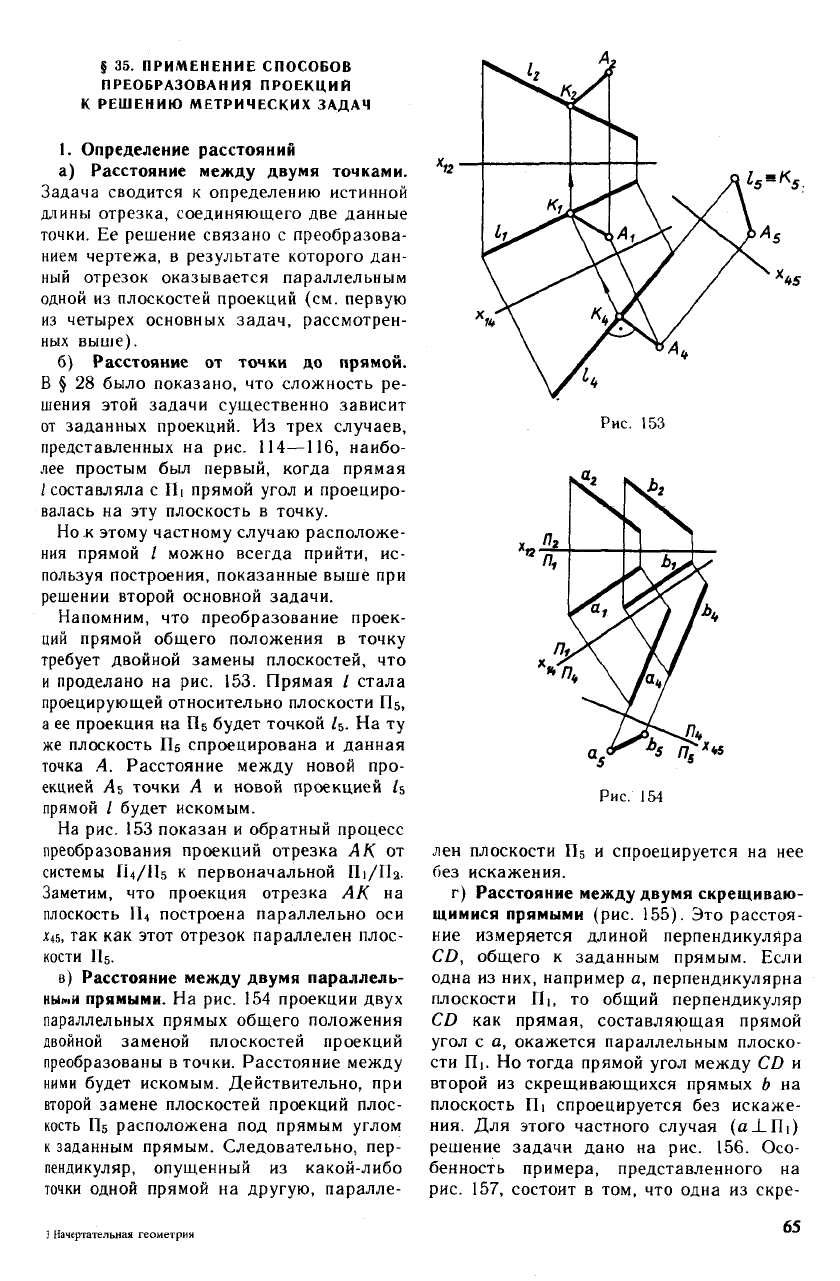
Напомним, что преобразование проек-

ций прямой общего положения в точку

требует двойной замены плоскостей, что

и проделано на рис. 153. Прямая / стала

проецирующей относительно плоскости Щ,

а ее проекция на Щ будет точкой /

. На ту

же плоскость П5 спроецирована и данная

точка А. Расстояние между новой про-

екцией Аь точки А и новой проекцией /5

прямой I будет искомым.

На рис. 153 показан и обратный процесс

преобразования проекций отрезка АК от

системы П4/Н5 к первоначальной П1/П2.

Заметим, что проекция отрезка АК на

плоскость 11

построена параллельно оси

Х45, так как этот отрезок параллелен плос-

кости lis.

в) Расстояние между двумя параллель-

ными прямыми. На рис. 154 проекции двух

параллельных прямых общего положения

двойной заменой плоскостей проекций

преобразованы в точки. Расстояние между

ними будет искомым. Действительно, при

второй замене плоскостей проекций плос-

кость П5 расположена под прямым углом

к заданным прямым. Следовательно, пер-

пендикуляр, опущенный из какой-либо

точки одной прямой на другую, паралле-

Рис. 153

лен плоскости П5 и спроецируется на нее

без искажения.

г) Расстояние между двумя скрещиваю-

щимися прямыми (рис. 155). Это расстоя-

ние измеряется длиной перпендикуляра

CD, общего к заданным прямым. Если

одна из них, например а, перпендикулярна

плоскости Г1ь то общий перпендикуляр

CD как прямая, составляющая прямой

угол с а, окажется параллельным плоско-

сти П). Но тогда прямой угол между CD и

второй из скрещивающихся прямых Ь на

плоскость Ш спроецируется без искаже-

ния. Для этого частного случая (a

_L П

решение задачи дано на рис. 156. Осо-

бенность примера, представленного на

рис. 157, состоит в том, что одна из скре-

3 Начертательная геометрия

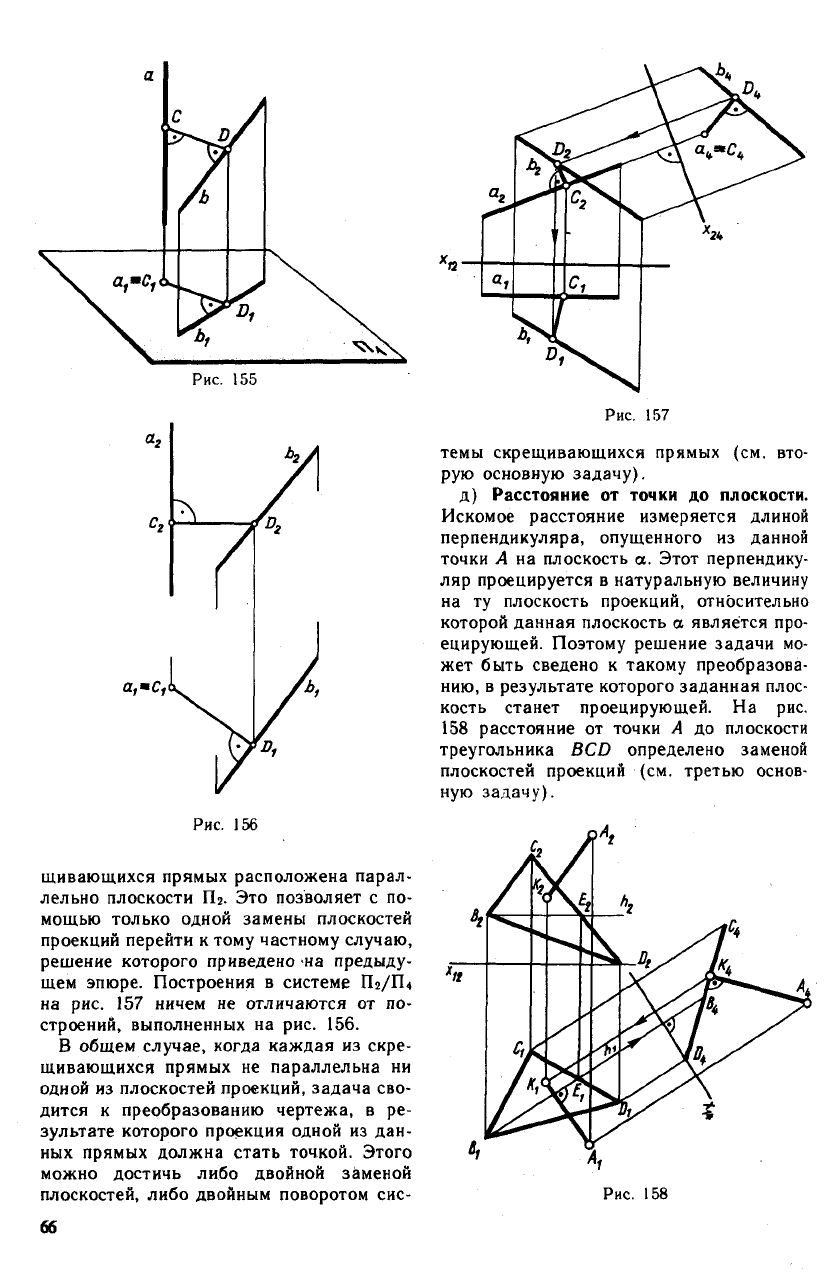
щивающихся прямых расположена парал-

лельно плоскости Пг. Это позволяет с по-

мощью только одной замены плоскостей

проекций перейти к тому частному случаю,

решение которого приведено на предыду-

щем эпюре. Построения в системе П2/П4

на рис. 157 ничем не отличаются от по-

строений, выполненных на рис. 156.

В общем случае, когда каждая из скре-

щивающихся прямых не параллельна ни

одной из плоскостей проекций, задача сво-

дится к преобразованию чертежа, в ре-

зультате которого проекция одной из дан-

ных прямых должна стать точкой. Этого

можно достичь либо двойной заменой

плоскостей, либо двойным поворотом сис-

темы скрещивающихся прямых (см. вто-

рую основную задачу),

д) Расстояние от точки до плоскости.

Искомое расстояние измеряется длиной

перпендикуляра, опущенного из данной

точки А на плоскость а. Этот перпендику-

ляр проецируется в натуральную величину

на ту плоскость проекций, относительно

которой данная плоскость а является про-

ецирующей. Поэтому решение задачи мо-

жет быть сведено к такому преобразова-

нию, в результате которого заданная плос-

кость станет проецирующей. На рис.

158 расстояние от точки А до плоскости

треугольника BCD определено заменой

плоскостей проекций (см. третью основ-

ную задачу).

Решение той же задачи без введения

новых плоскостей проекций дано на рис.

159, где проекции перпендикуляра р по-

строены с помощью главных линий плос-

кости а — горизонтали Л и фронтали f

(pi-LAi, p2±ft).

Основание перпендикуляра (точка К)

определено по известной схеме, а именно:

1) аэр(а1П

2) (1—2)=оПо,

3) К = рП(1-2).

Натуральная длина искомого расстоя-

ния

А\К\

найдена способом вращения.

е) Расстояние между двумя параллель-

ными плоскостями. В данном случае рас-

стояние измеряется длиной перпендикуля-

ра, опущенного из произвольной точки

одной плоскости на другую. Таким обра-

зом, эта задача сводится к предыдущей.

2. Определение углов

а) Угол между двумя пересекающимися

прямыми. На рис. 160 показано определе-

ние натуральной величины угла ВАС спо-

собом вращения. Плоскость угла враще-

нием вокруг горизонтали ВС приведена в

новое, горизонтальное положение, когда

горизонтальная проекция А\ вращающей-

ся вершины А оказалась удаленной от

проекции оси вращения на расстояние,

равное радиусу R

Решение задачи сводится к определе-

нию истинной величины радиуса R

, кото-

рый на рис. 160 найден способом враще-

ния. Плоскость окружности, которую опи-

сывает вершина угла А, обозначим через а

(olfiC, а так как ВС||Пь то о±П|).

з»

б) Угол между двумя скрещивающими-

ся прямыми. Мерой этого угла является

угол между двумя пересекающимися пря-

мыми, параллельными данным скрещива-

ющимся. Следовательно, и в этом случае

задача сводится к определению истинной

величины треугольника, что можно сде-

лать любым из известных способов.

в) Угол между прямой и плоскостью.

Углом прямой т с плоскостю о (рис. 161)

называется острый угол ср, составленный

этой прямой с ее проекцией на данную

плоскость. Построение проекций угла ср

требует определения двух точек К и 1,

первая из которых является точкой пе-

ресечения данной прямой с плоскостью а,

а вторая — основанием перпендикуляра,

опущенного из произвольной точки А пря-

мой на ту же плоскость. Получив две

пересекающиеся в точке К прямые (т и

/), определяем истинную величину угла

между ними так, как это было описано

выше в п. «а».

Если задача требует определения толь-

ко величины угла между прямой и плоско-

стью без изображения его проекций, то

решение можно значительно упростить,

опустив построение точек К и L.

Действительно, рассматривая прямоу-

гольный треугольник ALK (рис. 161), за-

мечаем, что

ср

= 90° —

г|>,

где

г|>

— угол, об-

разованный данной прямой т и перпенди-

куляром п к плоскости а.

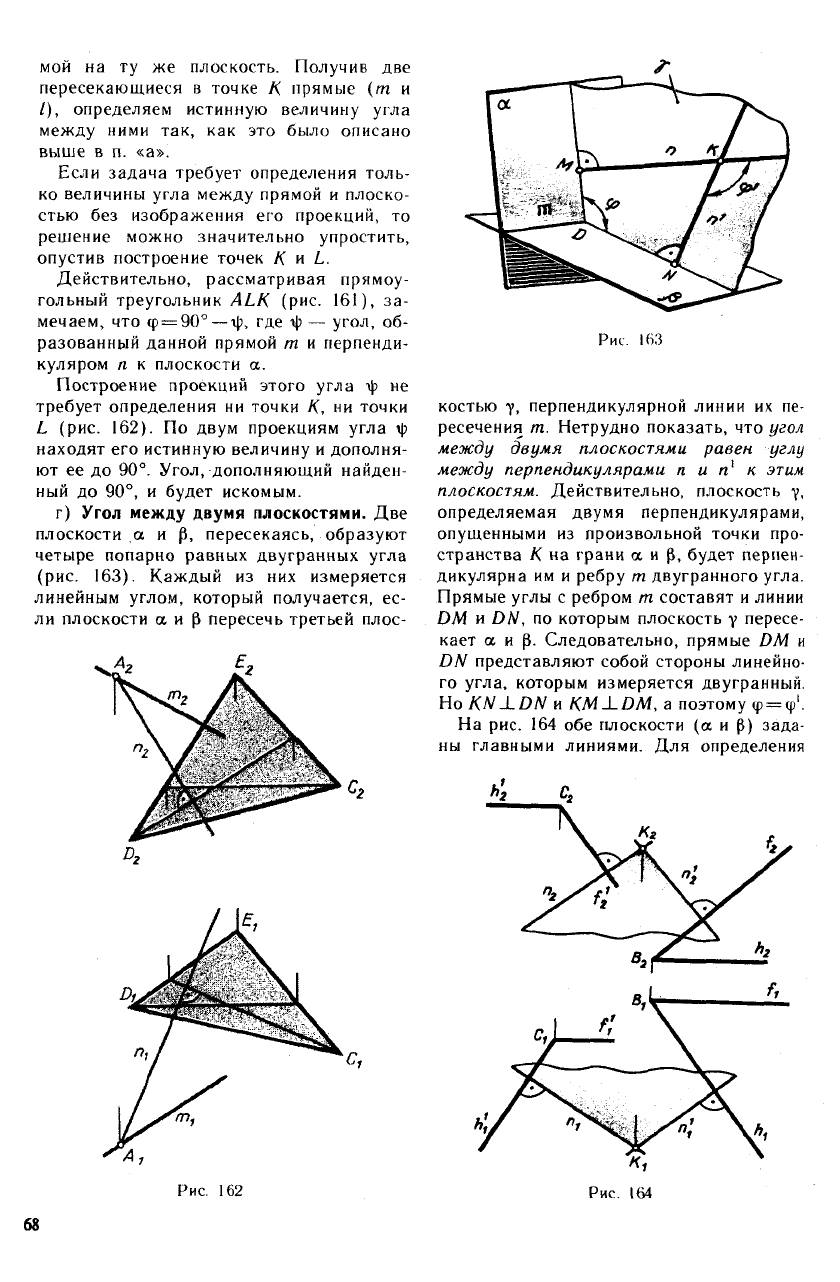
Построение проекций этого угла ф не

требует определения ни точки К, ни точки

L (рис. 162). По двум проекциям угла tf>

находят его истинную величину и дополня-

ют ее до 90°. Угол, дополняющий найден-

ный до 90°, и будет искомым.

г) Угол между двумя плоскостями. Две

плоскости а и р, пересекаясь, образуют

четыре попарно равных двугранных угла

(рис. 163). Каждый из них измеряется

линейным углом, который получается, ес-

ли плоскости аир пересечь третьей плос-

Рис. 163

костью у, перпендикулярной линии их пе-

ресечения т. Нетрудно показать, что угол

между двумя плоскостями равен углу

между перпендикулярами п и п' к этим

плоскостям. Действительно, плоскость у,

определяемая двумя перпендикулярами,

опущенными из произвольной точки про-

странства К на грани аир, будет перпен-

дикулярна им и ребру m двугранного угла.

Прямые углы с ребром m составят и линии

DM и DN, по которым плоскость у пересе-

кает аир. Следовательно, прямые DM и

DN представляют собой стороны линейно-

го угла, которым измеряется двугранный.

Но KN±DN и KM A-DM, а поэтому

= ф'.

На рис. 164 обе плоскости (а и Р) зада-

ны главными линиями. Для определения

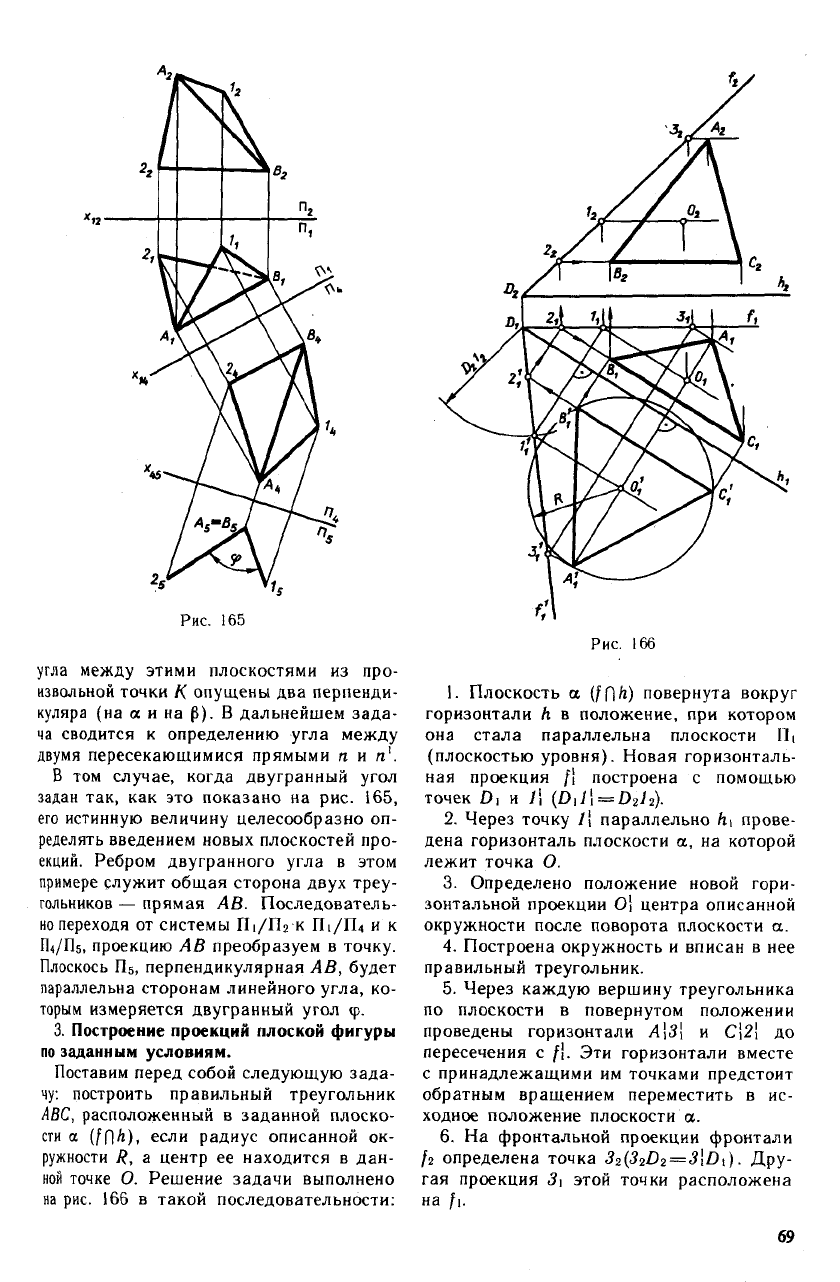
Рис. 165

угла между этими плоскостями из про-

извольной точки К опущены два перпенди-

куляра (на а и на Р). В дальнейшем зада-

ча сводится к определению угла между

двумя пересекающимися прямыми п и я'.

В том случае, когда двугранный угол

задан так, как это показано на рис. 165,

его истинную величину целесообразно оп-

ределять введением новых плоскостей про-

екций. Ребром двугранного угла в этом

примере служит общая сторона двух треу-

гольников — прямая АВ. Последователь-

но

переходя от системы П1/П2 к П1/П4 и к

П4/П5, проекцию АВ преобразуем в точку.

Плоскось П5, перпендикулярная АВ, будет

параллельна сторонам линейного угла, ко-

торым измеряется двугранный угол <р.

3. Построение проекций плоской фигуры

по заданным условиям.

Поставим перед собой следующую зада-

чу. построить правильный треугольник

ABC, расположенный в заданной плоско-

сти a

[ff\h),

если радиус описанной ок-

ружности R, а центр ее находится в дан-

ной точке О. Решение задачи выполнено

на рис. 166 в такой последовательности:

Рис. 166

1. Плоскость а (/П^) повернута вокруг

горизонтали h в положение, при котором

она стала параллельна плоскости П|

(плоскостью уровня). Новая горизонталь-

ная проекция /1 построена с помощью

точек D, и }\ (£>,/! = D

2. Через точку /| параллельно h\ прове-

дена горизонталь плоскости а, на которой

лежит точка О.

3. Определено положение новой гори-

зонтальной проекции О, центра описанной

окружности после поворота плоскости а.

4. Построена окружность и вписан в нее

правильный треугольник.

5. Через каждую вершину треугольника

по плоскости в повернутом положении

проведены горизонтали Л|3! и С\2\ до

пересечения с Эти горизонтали вместе

с принадлежащими им точками предстоит

обратным вращением переместить в ис-

ходное положение плоскости а.

6. На фронтальной проекции фронтали

определена точка <?

(<?2£>2=<?!£>О. Дру-

гая проекция 31 этой точки расположена

на /1.