Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

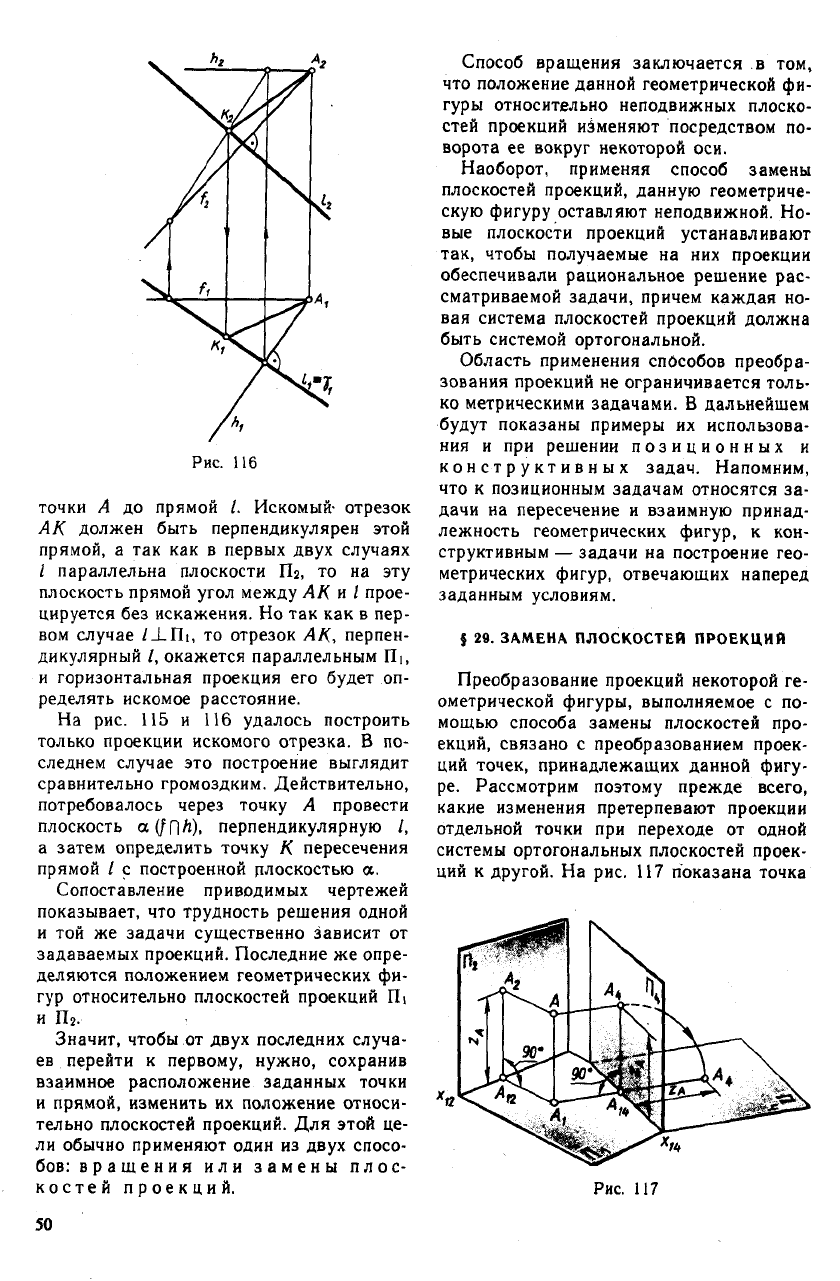
точки А до прямой /. Искомый- отрезок

АК должен быть перпендикулярен этой

прямой, а так как в первых двух случаях

I параллельна плоскости П2, то на эту

плоскость прямой угол между А К и / прое-

цируется без искажения. Но так как в пер-

вом случае /ХШ, то отрезок АК, перпен-

дикулярный /, окажется параллельным Пь

и горизонтальная проекция его будет оп-

ределять искомое расстояние.

На рис. 115 и 116 удалось построить

только проекции искомого отрезка. В по-

следнем случае это построение выглядит

сравнительно громоздким. Действительно,

потребовалось через точку А провести

плоскость а(/Г|Л), перпендикулярную I,

а затем определить точку К пересечения

прямой I с построенной плоскостью а.

Сопоставление приводимых чертежей

показывает, что трудность решения одной

и той же задачи существенно зависит от

задаваемых проекций. Последние же опре-

деляются положением геометрических фи-

гур относительно плоскостей проекций П1

и П

Значит, чтобы от двух последних случа-

ев перейти к первому, нужно, сохранив

взаимное расположение заданных точки

и прямой, изменить их положение относи-

тельно плоскостей проекций. Для этой це-

ли обычно применяют один из двух спосо-

бов: вращения или замены плос-

костей проекций.

Способ вращения заключается в том,

что положение данной геометрической фи-

гуры относительно неподвижных плоско-

стей проекций изменяют посредством по-

ворота ее вокруг некоторой оси.

Наоборот, применяя способ замены

плоскостей проекций, данную геометриче-

скую фигуру оставляют неподвижной. Но-

вые плоскости проекций устанавливают

так, чтобы получаемые на них проекции

обеспечивали рациональное решение рас-

сматриваемой задачи, причем каждая но-

вая система плоскостей проекций должна

быть системой ортогональной.

Область применения способов преобра-

зования проекций не ограничивается толь-

ко метрическими задачами. В дальнейшем

будут показаны примеры их использова-

ния и при решении позиционных и

конструктивных задач. Напомним,

что к позиционным задачам относятся за-

дачи на пересечение и взаимную принад-

лежность геометрических фигур, к кон-

структивным — задачи на построение гео-

метрических фигур, отвечающих наперед

заданным условиям.

§ 29. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Преобразование проекций некоторой ге-

ометрической фигуры, выполняемое с по-

мощью способа замены плоскостей про-

екций, связано с преобразованием проек-

ций точек, принадлежащих данной фигу-

ре. Рассмотрим поэтому прежде всего,

какие изменения претерпевают проекции

отдельной точки при переходе от одной

системы ортогональных плоскостей проек-

ций к другой. На рис. 117 показана точка

Рис. 131 Рис. 132 Рис. 133

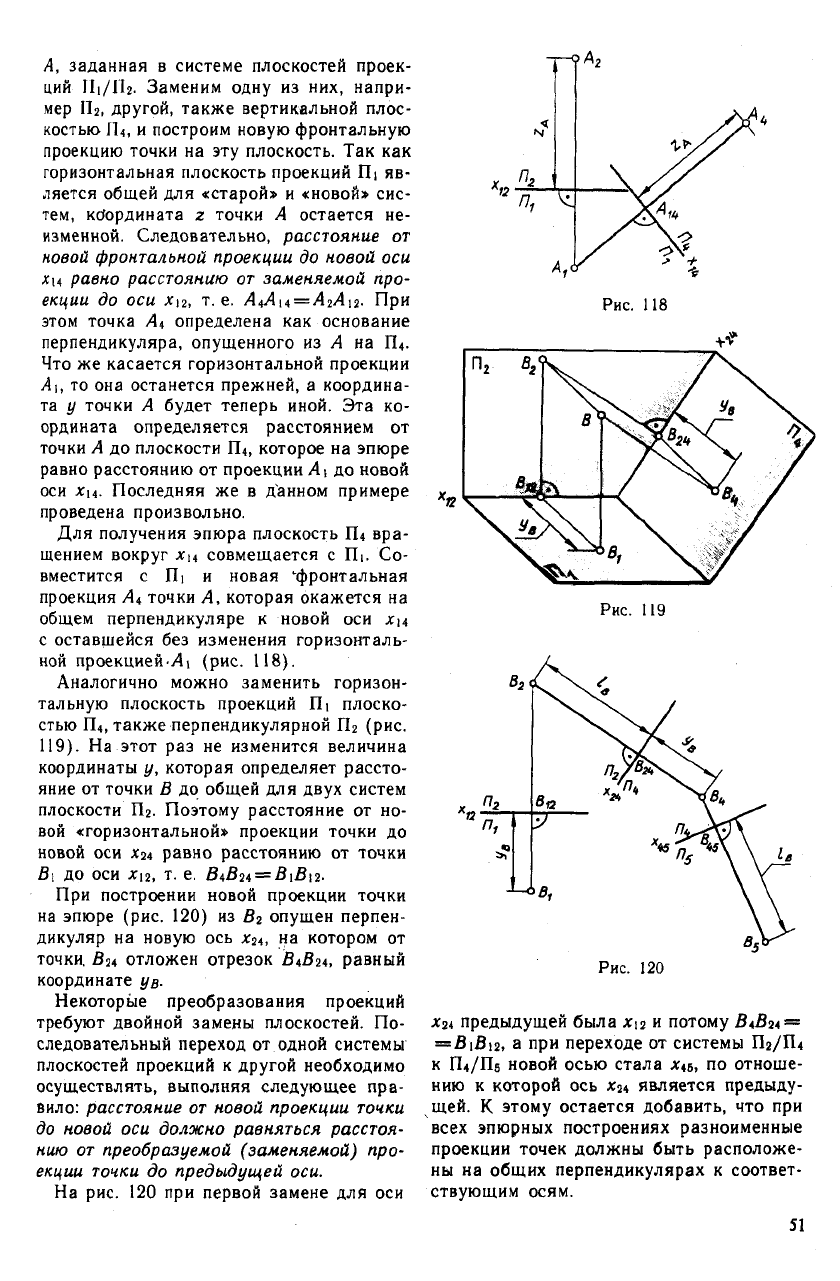
А, заданная в системе плоскостей проек-

ций II1/II2. Заменим одну из них, напри-

мер Пг, другой, также вертикальной плос-

костью П4, и построим новую фронтальную

проекцию точки на эту плоскость. Так как

горизонтальная плоскость проекций П| яв-

ляется общей для «старой» и «новой» сис-

тем, координата z точки А остается не-

изменной. Следовательно, расстояние от

новой фронтальной проекции до новой оси

хи равно расстоянию от заменяемой про-

екции до оси X12, т.е. АьА\ц = А

А\г. При

этом точка Ai определена как основание

перпендикуляра, опущенного из А на П

Что же касается горизонтальной проекции

At, то она останется прежней, а координа-

та у точки А будет теперь иной. Эта ко-

ордината определяется расстоянием от

точки А до плоскости П4, которое на эпюре

равно расстоянию от проекции А\ до новой

оси Хц. Последняя же в данном примере

проведена произвольно.

Для получения эпюра плоскость Ш вра-

щением вокруг хц совмещается с П|. Со-

вместится с П1 и новая 'фронтальная

проекция А

точки А, которая окажется на

общем перпендикуляре к новой оси хы

с оставшейся без изменения горизонталь-

ной проекцией/^ (рис. 118).

Аналогично можно заменить горизон-

тальную плоскость проекций П| плоско-

стью П

также перпендикулярной П

(рис.

119). На этот раз не изменится величина

координаты у, которая определяет рассто-

яние от точки В до общей для двух систем

плоскости Пг. Поэтому расстояние от но-

вой «горизонтальной» проекции точки до

новой оси *24 равно расстоянию от точки

В\ до оси *i2, т. е. ВаВц =

В\В\2.

При построении новой проекции точки

на эпюре (рис. 120) из В

опущен перпен-

дикуляр на новую ось хц, на котором от

точки. В24 отложен отрезок В^Вц, равный

координате ув-

Некоторые преобразования проекций

требуют двойной замены плоскостей. По-

следовательный переход от одной системы

плоскостей проекций к другой необходимо

осуществлять, выполняя следующее пра-

вило: расстояние от новой проекции точки

до новой оси должно равняться расстоя-

нию от преобразуемой (заменяемой) про-

екции точки до предыдущей оси.

На рис. 120 при первой замене для оси

Рис. 118

в*

? '

Рис. 119

Рис. 120

JE24 предыдущей была х\2 и потому В*Вц =

В\В\г,

а при переходе от системы Пг/П

к П4/П5 новой осью стала х

б, по отноше-

нию к которой ось является предыду-

щей. К этому остается добавить, что при

всех эпюрных построениях разноименные

проекции точек должны быть расположе-

ны на общих перпендикулярах к соответ-

ствующим осям.

§ 30. РЕШЕНИЕ ЧЕТЫРЕХ ОСНОВНЫХ

ЗАДАЧ СПОСОБОМ ЗАМЕНЫ

ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Все метрические и позиционные задачи,

решаемые способом замены плоскостей

проекций, можно свести к одной из следу-

ющих четырех.

Задача 1. Преобразовать чертеж так,

чтобы прямая общего положения оказа-

лась параллельной одной из плоскостей

проекций новой системы.

На рис. 121 показана прямая а, которая

в системе П1/П2 является прямой общего

положения.

Для решения задачи взята новая плос-

кость П*, отвечающая двум условиям:

-1-П| и П

||а. В системе П4/П1 прямая

а стала фронталью, а потому xullai. На

плоскость П4 без искажения проецируются

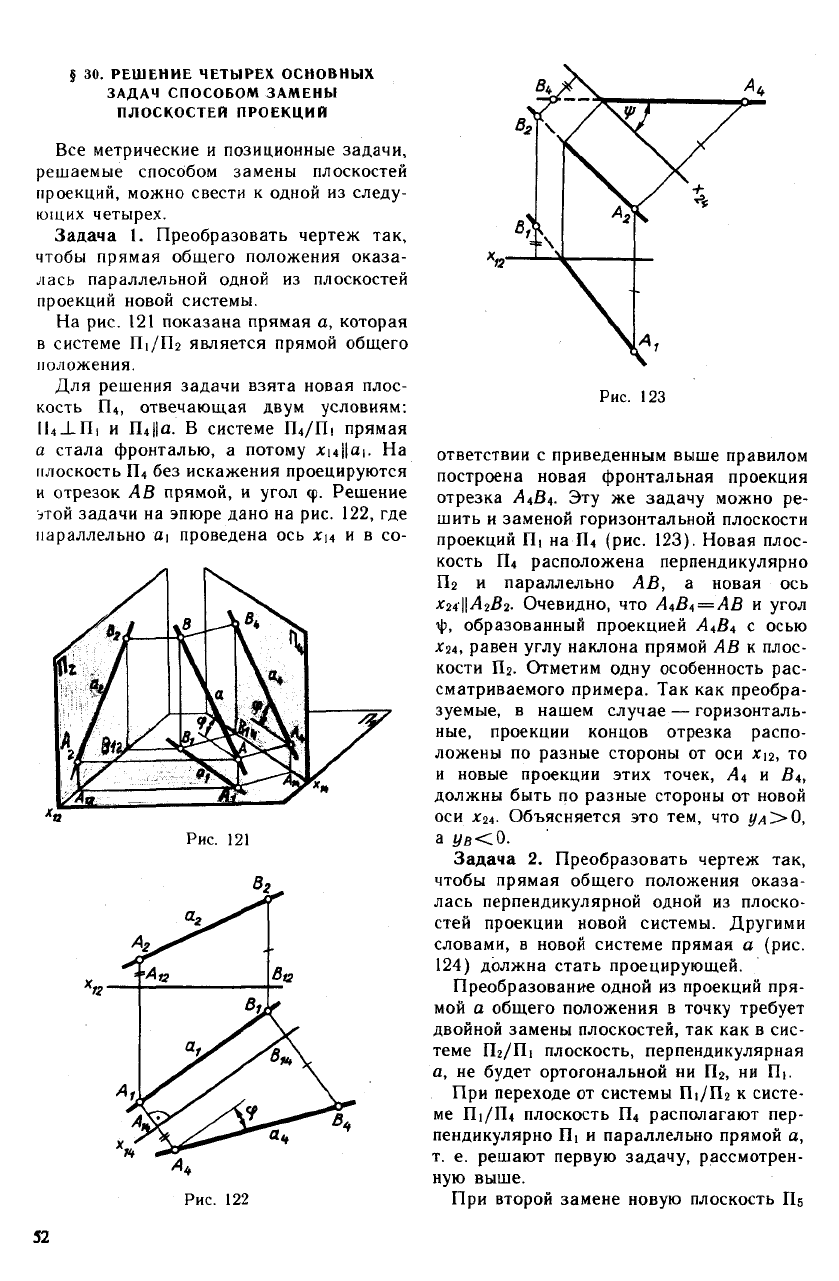
и отрезок АВ прямой, и угол (р. Решение

этой задачи на эпюре дано на рис. 122, где

параллельно а\ проведена ось хц и в со-

ответствии с приведенным выше правилом

построена новая фронтальная проекция

отрезка А^ВА- Эту же задачу можно ре-

шить и заменой горизонтальной плоскости

проекций П| наTU (рис. 123). Новая плос-

кость П4 расположена перпендикулярно

Пг и параллельно АВ, а новая ось

*24'||А

Вч. Очевидно, что

А*ВА

= АВ И угол

•ф, образованный проекцией А^В^ с осью

хц, равен углу наклона прямой АВ к плос-

кости П

. Отметим одну особенность рас-

сматриваемого примера. Так как преобра-

зуемые, в нашем случае — горизонталь-

ные, проекции концов отрезка распо-

ложены по разные стороны от оси х\

, то

и новые проекции этих точек, At и В

должны быть по разные стороны от новой

оси х

. Объясняется это тем, что ул>0,

а Ув<0.

Задача 2. Преобразовать чертеж так,

чтобы прямая общего положения оказа-

лась перпендикулярной одной из плоско-

стей проекции новой системы. Другими

словами, в новой системе прямая а (рис.

124) должна стать проецирующей.

Преобразование одной из проекций пря-

мой а общего положения в точку требует

двойной замены плоскостей, так как в сис-

теме П2/П1 плоскость, перпендикулярная

а, не будет ортогональной ни П

, ни Ш.

При переходе от системы П|/П

к систе-

ме П)/П

плоскость П

располагают пер-

пендикулярно П1 и параллельно прямой а,

т. е. решают первую задачу, рассмотрен-

ную выше.

При второй замене новую плоскость П5

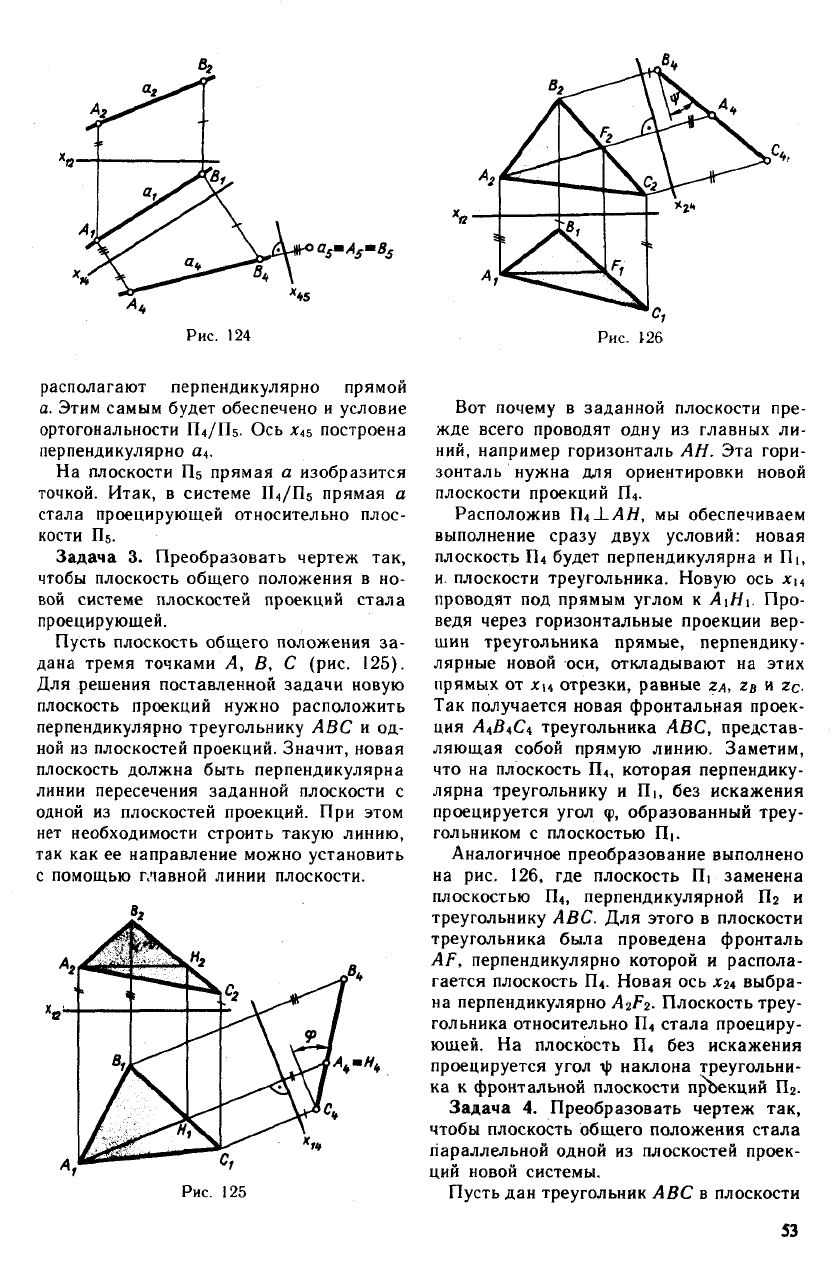
Рис. 124

Рис. 126

располагают перпендикулярно прямой

а. Этим самым будет обеспечено и условие

ортогональности П4/П5. Ось х

построена

перпендикулярно а

На плоскости П5 прямая а изобразится

точкой. Итак, в системе Н4/П5 прямая а

стала проецирующей относительно плос-

кости П5.

Задача 3. Преобразовать чертеж так,

чтобы плоскость общего положения в но-

вой системе плоскостей проекций стала

проецирующей.

Пусть плоскость общего положения за-

дана тремя точками А, В, С (рис. 125).

Для решения поставленной задачи новую

плоскость проекций нужно расположить

перпендикулярно треугольнику ABC и од-

ной из плоскостей проекций. Значит, новая

плоскость должна быть перпендикулярна

линии пересечения заданной плоскости с

одной из плоскостей проекций. При этом

нет необходимости строить такую линию,

так как ее направление можно установить

с помощью главной линии плоскости.

Вот почему в заданной плоскости пре-

жде всего проводят одну из главных ли-

ний, например горизонталь АН. Эта гори-

зонталь нужна для ориентировки новой

плоскости проекций П4.

Расположив Щ-L/l/f, мы обеспечиваем

выполнение сразу двух условий: новая

плоскость П4 будет перпендикулярна и П|,

и. плоскости треугольника. Новую ось хц

проводят под прямым углом к А\Н\. Про-

ведя через горизонтальные проекции вер-

шин треугольника прямые, перпендику-

лярные новой оси, откладывают на этих

прямых от xi4 отрезки, равные Г A, ZB И ZC•

Так получается новая фронтальная проек-

ция A^BiCi треугольника ABC, представ-

ляющая собой прямую линию. Заметим,

что на плоскость П

, которая перпендику-

лярна треугольнику и Пь без искажения

проецируется угол <р, образованный треу-

гольником с ПЛОСКОСТЬЮ П|.

Аналогичное преобразование выполнено

на рис. 126, где плоскость П1 заменена

плоскостью П4, перпендикулярной Пг и

треугольнику ABC. Для этого в плоскости

треугольника была проведена фронталь

AF, перпендикулярно которой и распола-

гается плоскость П

. Новая ось х

выбра-

на перпендикулярно A2F2. Плоскость треу-

гольника относительно П

стала проециру-

ющей. На плоскость П

без искажения

проецируется угол t|> наклона треугольни-

ка к фронтальной плоскости проекций П

Задача 4. Преобразовать чертеж так,

чтобы плоскость общего положения стала

параллельной одной из плоскостей проек-

ций новой системы.

Пусть дан треугольник ABC в плоскости

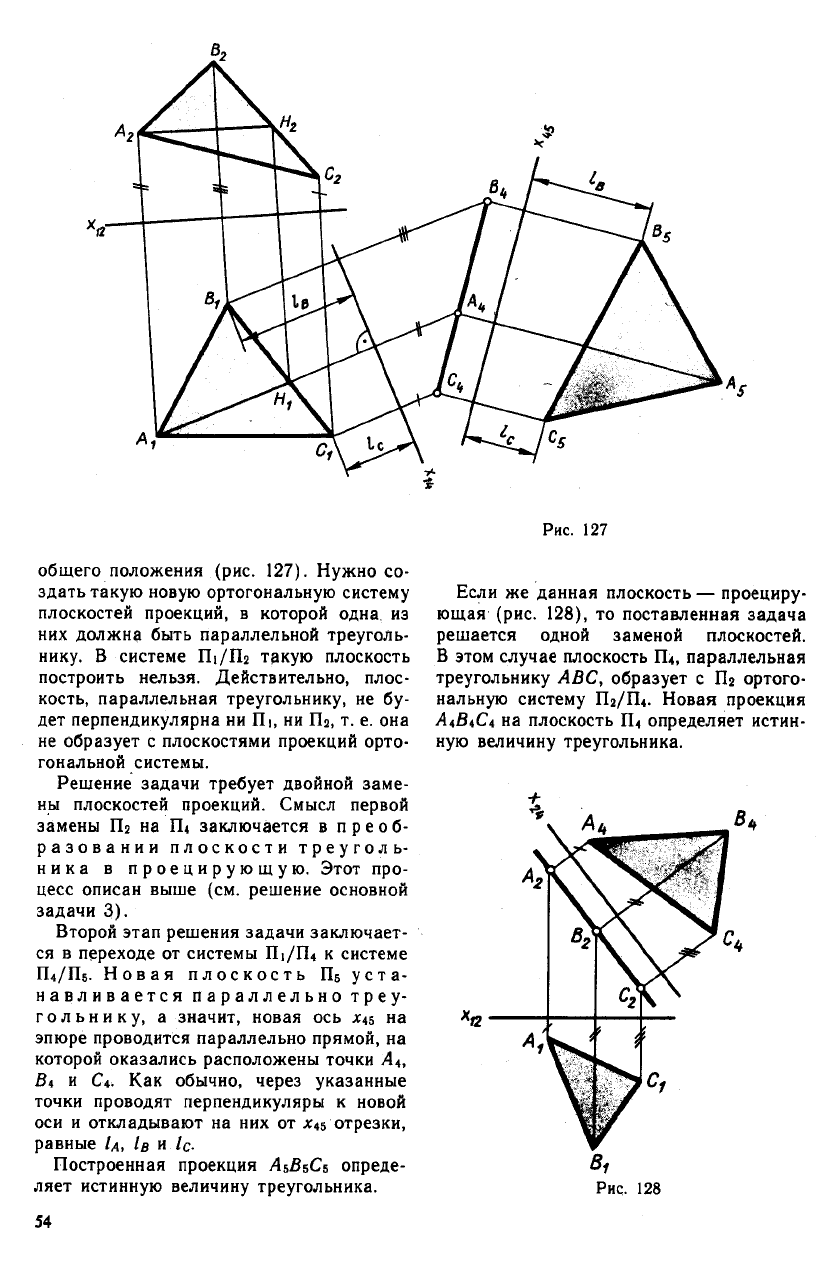
общего положения (рис. 127). Нужно со-

здать такую новую ортогональную систему

плоскостей проекций, в которой одна из

них должна быть параллельной треуголь-

нику. В системе П1/П2 такую плоскость

построить нельзя. Действительно, плос-

кость, параллельная треугольнику, не бу-

дет перпендикулярна ни П|, ни П

, т. е. она

не образует с плоскостями проекций орто-

гональной системы.

Решение задачи требует двойной заме-

ны плоскостей проекций. Смысл первой

замены Пг на П< заключается в преоб-

разовании плоскости треуголь-

ника в проецирующую. Этот про-

цесс описан выше (см. решение основной

задачи 3).

Второй этап решения задачи заключает-

ся в переходе от системы П1/П4 к системе

П4/П5. Новая плоскость Щ уста-

навливается параллельно треу-

гольнику, а значит, новая ось jc

s на

эпюре проводится параллельно прямой, на

которой оказались расположены точки Л

и С

, Как обычно, через указанные

точки проводят перпендикуляры к новой

оси и откладывают на них от х

5 отрезки,

равные 1А, 1В и

1С-

Построенная проекция Л5В5С5 опреде-

ляет истинную величину треугольника.

Рис. 127

Если же данная плоскость — проециру-

ющая (рис. 128), то поставленная задача

решается одной заменой плоскостей.

В этом случае плоскость Щ, параллельная

треугольнику ABC, образует с Пг ортого-

нальную систему П2/П4. Новая проекция

Л4В4С4 на плоскость П4 определяет истин-

ную величину треугольника.

Рис.

131

Рис.

132

Рис. 133

§ 31. СПОСОБ ВРАЩЕНИЯ

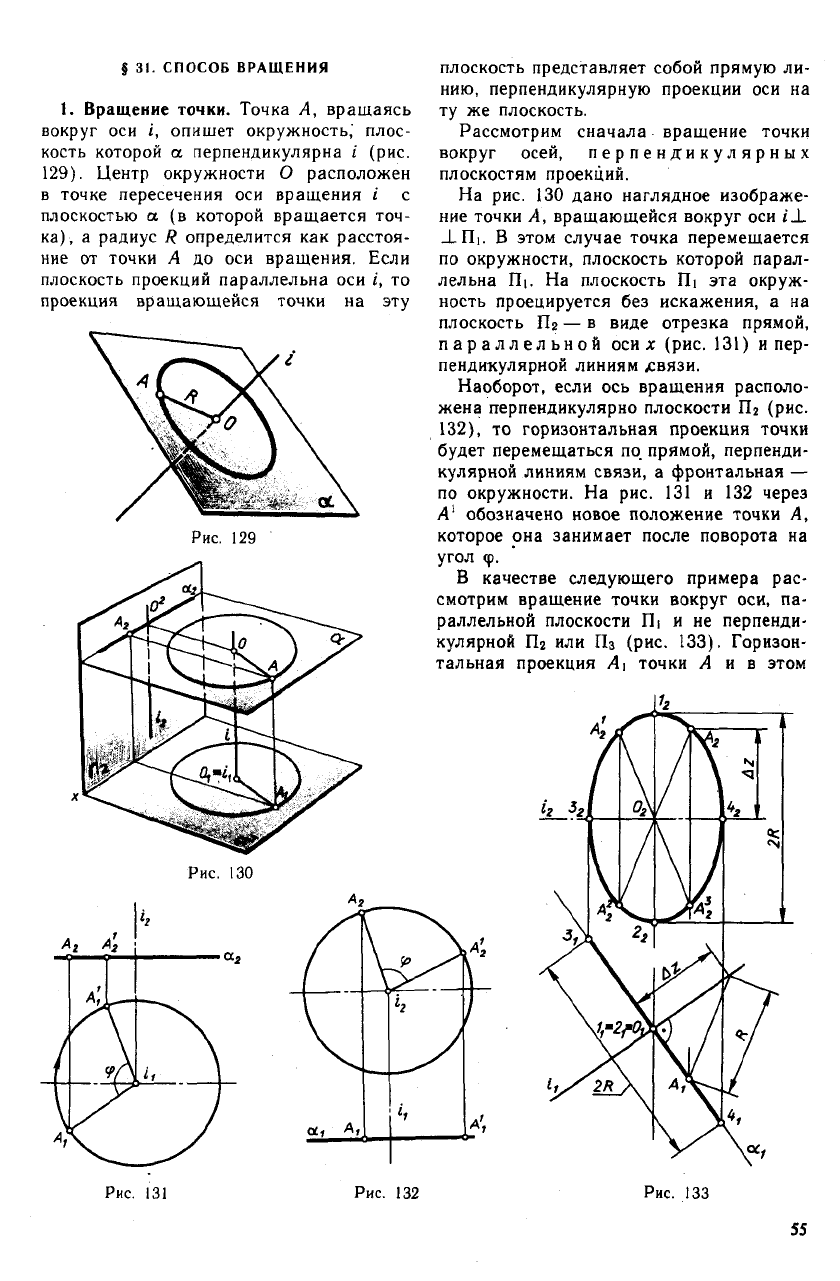
1. Вращение точки. Точка А, вращаясь

вокруг оси /, опишет окружность,' плос-

кость которой а перпендикулярна г (рис.

129). Центр окружности О расположен

в точке пересечения оси вращения г с

плоскостью а (в которой вращается точ-

ка), а радиус R определится как расстоя-

ние от точки А до оси вращения. Если

плоскость проекций параллельна оси г, то

проекция вращающейся точки на эту

Рис. 129

Рис. 130

плоскость представляет собой прямую ли-

нию, перпендикулярную проекции оси на

ту же плоскость.

Рассмотрим сначала вращение точки

вокруг осей, перпендикулярных

плоскостям проекций.

На рис. 130 дано наглядное изображе-

ние точки А, вращающейся вокруг оси i_L

_L Hi. В этом случае точка перемещается

по окружности, плоскость которой парал-

лельна П1. На плоскость П1 эта окруж-

ность проецируется без искажения, а на

плоскость Пг — в виде отрезка прямой,

параллельной оси х (рис. 131) и пер-

пендикулярной линиям лвязи.

Наоборот, если ось вращения располо-

жена перпендикулярно плоскости Пг (рис.

132), то горизонтальная проекция точки

будет перемещаться по. прямой, перпенди-

кулярной линиям связи, а фронтальная —

по окружности. На рис. 131 и 132 через

обозначено новое положение точки А,

которое она занимает после поворота на

угол «р.

В качестве следующего примера рас-

смотрим вращение точки вокруг оси, па-

раллельной плоскости П| и не перпенди-

кулярной Пг или Пз (рис. 133). Горизон-

тальная проекция А] точки А и в этом

Рис. 131

Рис. 132

Рис. 133

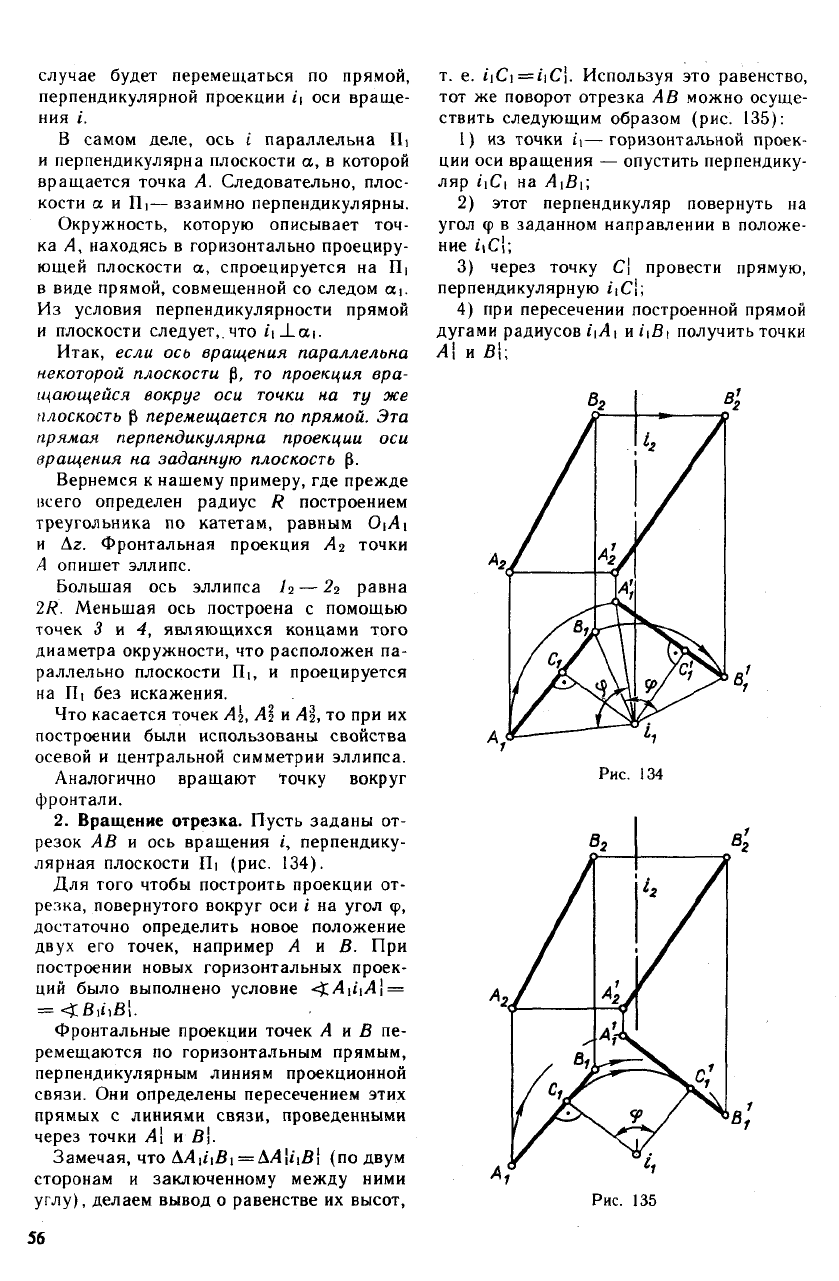
случае будет перемещаться по прямой,

перпендикулярной проекции i\ оси враще-

ния i.

В самом деле, ось i параллельна П)

и перпендикулярна плоскости а, в которой

вращается точка А. Следовательно, плос-

кости а и П,— взаимно перпендикулярны.

Окружность, которую описывает точ-

ка А, находясь в горизонтально проециру-

ющей плоскости а, спроецируется на П|

в виде прямой, совмещенной со следом oci.

Из условия перпендикулярности прямой

и плоскости следует,.что ii_Lai.

Итак, если ось вращения параллельна

некоторой плоскости р, то проекция вра-

щающейся вокруг оси точки на ту же

плоскость р перемещается по прямой. Эта

прямая перпендикулярна проекции оси

вращения на заданную плоскость р.

Вернемся к нашему примеру, где прежде

нсего определен радиус R построением

треугольника по катетам, равным 0\Ai

и Дг. Фронтальная проекция Л

точки

А опишет эллипс.

Большая ось эллипса /

— 2

равна

2R. Меньшая ось построена с помощью

точек 3 И 4, являющихся концами того

диаметра окружности, что расположен па-

раллельно плоскости Пь и проецируется

на Hi без искажения.

Что касается точек Лг, Аг и Л|, то при их

построении были использованы свойства

осевой и центральной симметрии эллипса.

Аналогично вращают Точку вокруг

фронтали.

2. Вращение отрезка. Пусть заданы от-

резок АВ и ось вращения <', перпендику-

лярная плоскости П] (рис. 134).

Для того чтобы построить проекции от-

резка, повернутого вокруг оси i на угол ф,

достаточно определить новое положение

двух его точек, например Л и В. При

построении новых горизонтальных проек-

ций было выполнено условие <£A\i\A\ =

= <BxhB\.

Фронтальные проекции точек А и В пе-

ремещаются по горизонтальным прямым,

перпендикулярным линиям проекционной

связи. Они определены пересечением этих

прямых с линиями связи, проведенными

через точки А\ и В\.

Замечая, что

ДЛ

\i\B\ =

ДЛ|<1В|

(по двум

сторонам и заключенному между ними

углу), делаем вывод о равенстве их высот,

т. е. i\Ci=i]C\. Используя это равенство,

тот же поворот отрезка АВ можно осуще-

ствить следующим образом (рис. 135):

1) из точки i 1— горизонтальной проек-

ции оси вращения — опустить перпендику-

ляр i\C\ на А\В\\

2) этот перпендикуляр повернуть на

угол ф в заданном направлении в положе-

ние t'iC|;

3) через точку С| провести прямую,

перпендикулярную йС\;

4) при пересечении построенной прямой

дугами радиусов г'|Л) и иВ\ получить точки

Л i

и В1;

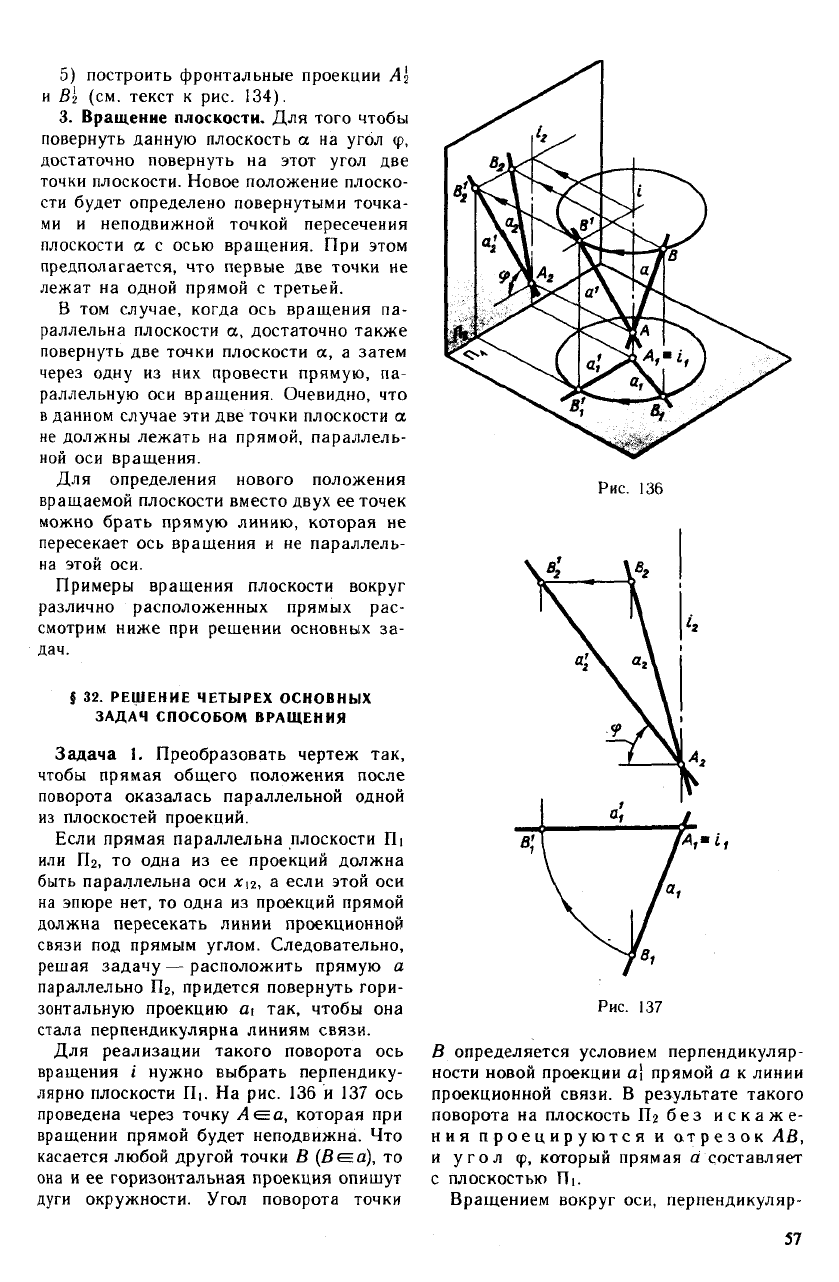
5) построить фронтальные проекции Л

и (см. текст к рис. 134).

3. Вращение плоскости. Для того чтобы

повернуть данную плоскость а на угол ф,

достаточно повернуть на этот угол две

точки плоскости. Новое положение плоско-

сти будет определено повернутыми точка-

ми и неподвижной точкой пересечения

плоскости а с осью вращения. При этом

предполагается, что первые две точки не

лежат на одной прямой с третьей.

В том случае, когда ось вращения па-

раллельна плоскости а, достаточно также

повернуть две точки плоскости а, а затем

через одну из них провести прямую, па-

раллельную оси вращения. Очевидно, что

в данном случае эти две точки плоскости а

не должны лежать на прямой, параллель-

ной оси вращения.

Для определения нового положения

вращаемой плоскости вместо двух ее точек

можно брать прямую линию, которая не

пересекает ось вращения и не параллель-

на этой оси.

Примеры вращения плоскости вокруг

различно расположенных прямых рас-

смотрим ниже при решении основных за-

дач.

§ 32. РЕШЕНИЕ ЧЕТЫРЕХ ОСНОВНЫХ

ЗАДАЧ СПОСОБОМ ВРАЩЕНИЯ

Задача 1. Преобразовать чертеж так,

чтобы прямая общего положения после

поворота оказалась параллельной одной

из плоскостей проекций.

Если прямая параллельна плоскости Ш

или Пг, то одна из ее проекций должна

быть параллельна оси х\2, а если этой оси

на эпюре нет, то одна из проекций прямой

должна пересекать линии проекционной

связи под прямым углом. Следовательно,

решая задачу — расположить прямую а

параллельно Пг, придется повернуть гори-

зонтальную проекцию щ так, чтобы она

стала перпендикулярна линиям связи.

Для реализации такого поворота ось

вращения i нужно выбрать перпендику-

лярно плоскости П,. На рис. 136 и 137 ось

проведена через точку Леа, которая при

вращении прямой будет неподвижна. Что

касается любой другой точки В (В^.а), то

она и ее горизонтальная проекция опишут

дуги окружности. Угол поворота точки

Рис. 136

Рис. 137

В определяется условием перпендикуляр-

ности новой проекции а\ прямой а к линии

проекционной связи. В результате такого

поворота на плоскость Щбез искаже-

ния проецируются и отрезок АВ,

и угол ф, который прямая а составляет

с плоскостью Пь

Вращением вокруг оси, перпендикуляр-

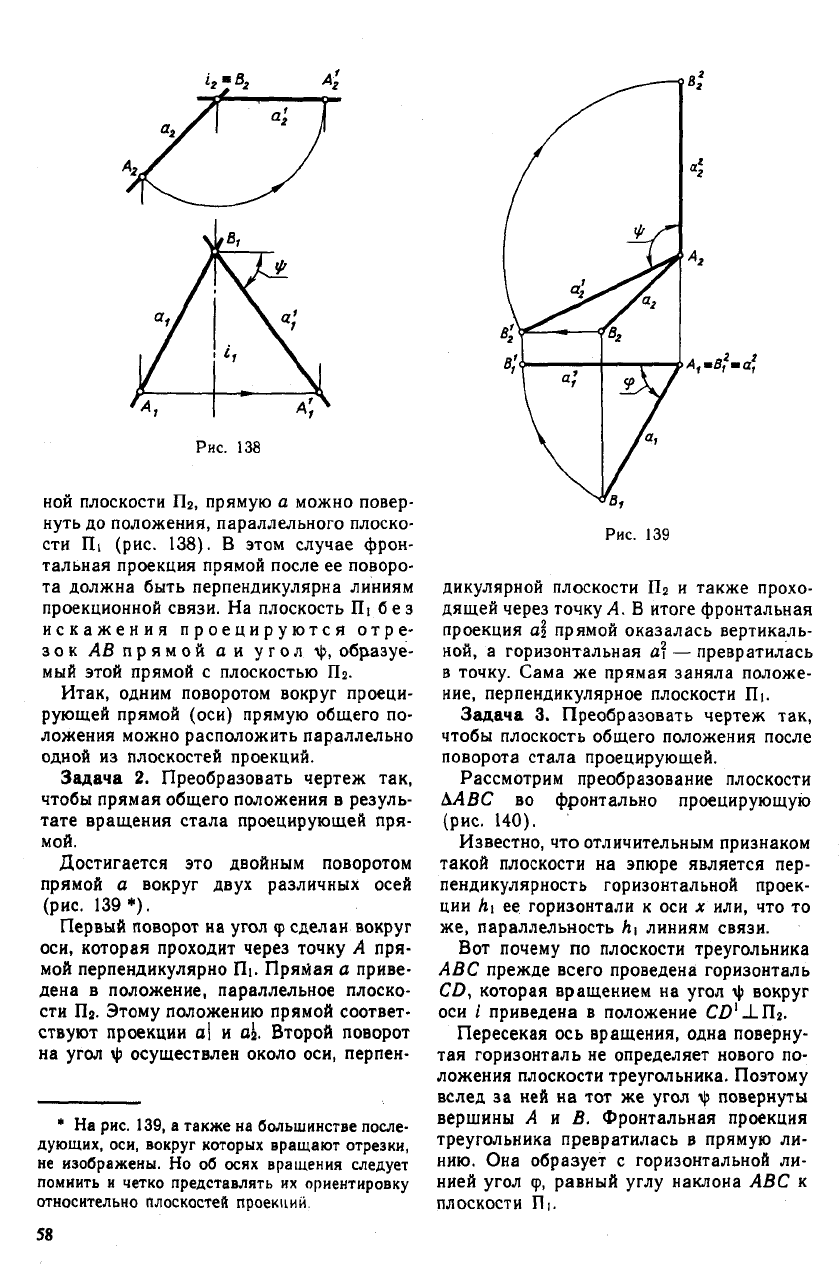
ной плоскости Пг, прямую а можно повер-

нуть до положения, параллельного плоско-

сти П1 (рис. 138). В этом случае фрон-

тальная проекция прямой после ее поворо-

та должна быть перпендикулярна линиям

проекционной связи. На плоскость П| без

искажения проецируются отре-

зок АВ прямой аи угол -ф, образуе-

мый этой прямой с плоскостью Пг.

Итак, одним поворотом вокруг проеци-

рующей прямой (оси) прямую общего по-

ложения можно расположить параллельно

одной из плоскостей проекций.

Задача 2. Преобразовать чертеж так,

чтобы прямая общего положения в резуль-

тате вращения стала проецирующей пря-

мой.

Достигается это двойным поворотом

прямой а вокруг двух различных осей

(рис. 139*).

Первый поворот на угол ф сделан вокруг

оси, которая проходит через точку А пря-

мой перпендикулярно П1. Пряйая а приве-

дена в положение, параллельное плоско-

сти П2. Этому положению прямой соответ-

ствуют проекции а! и oj. Второй поворот

на угол осуществлен около оси, перпен-

* На рис. 139, а также на большинстве после-

дующих, оси, вокруг которых вращают отрезки,

не изображены. Но об осях вращения следует

помнить и четко представлять их ориентировку

относительно плоскостей проекций.

дикулярной плоскости П

и также прохо-

дящей через точку А. В итоге фронтальная

проекция al прямой оказалась вертикаль-

ной, а горизонтальная а? — превратилась

в точку. Сама же прямая заняла положе-

ние, перпендикулярное плоскости Пь

Задача 3. Преобразовать чертеж так,

чтобы плоскость общего положения после

поворота стала проецирующей.

Рассмотрим преобразование плоскости

ЬАВС во фронтально проецирующую

(рис. 140).

Известно, что отличительным признаком

такой плоскости на эпюре является пер-

пендикулярность горизонтальной проек-

ции Ai ее горизонтали к оси х или, что то

же, параллельность h\ линиям связи.

Вот почему по плоскости треугольника

ABC прежде всего проведена горизонталь

CD, которая вращением на угол г|) вокруг

оси i приведена в положение CZ)'±n

Пересекая ось вращения, одна поверну-

тая горизонталь не определяет нового по-

ложения плоскости треугольника. Поэтому

вслед за ней на тот же угол \|> повернуты

вершины А и В. Фронтальная проекция

треугольника превратилась в прямую ли-

нию. Она образует с горизонтальной ли-

нией угол ф, равный углу наклона ABC к

плоскости П|.

Задача 4. Преобразовать чертеж так,

чтобы плоскость общего положения в ре-

зультате вращения оказалась параллель-

ной одной из плоскостей проекций.

Приведем сначала то решение задачи,

когда осями вращения служат проецирую-

щие прямые. Первый поворот треугольни-

ка ABC был сделан вокруг вертикальной

оси, проходящей через вершину С (рис.

141).

В результате плоскость общего положе-

ния стала фронтально проецирующей,

т. е. первый этап преобразования является

точным повторением решения задачи

3. Далее можно проделать второй поворот

на угол ф вокруг оси, проходящей через

вершину В' перпендикулярно плоскости

Пг. Фронтальные проекции всех вершин

треугольника будут перемещаться по кон-

центрическим дугам, проведенным из точ-

ки В\ как из центра, а горизонтальные —

по прямым, перпендикулярным линиям

связи. После поворота на угол ф плоскость

треугольника оказалась параллельной П|.

Следовательно, горизонтальная проекция

А\В\С\

треугольника без искажения опре-

деляет его форму.

Покажем теперь, что эту задачу можно

решить менее громоздким способом —

вращением вокруг только одной оси.

Если задаться целью: одним поворотом

расположить треугольник параллельно

плоскости Пь то за ось вращения следует

принять такую прямую в плоскости треу-

гольника, которая еще до вращения была

бы параллельна Пи т. е. одну из его гори-

зонталей. На рис. 142 такой горизонталью

является прямая CD. Не повторяя всех

пояснений, содержащихся в п. 1 предыду-

щего параграфа, где рассматривалось

вращение точки вокруг горизонтали, отме-.

тим главное в предстоящем построении:

в тот момент, когда плоскость треугольни-

ка будет параллельна Пь горизонтальные

проекции каждой из перемещающихся

вершин окажутся удаленными от оси вра-

щения на расстояние, равное радиусу вра-

щения данной точки. Дальнейшие постро-

ения выполняются в такой последователь-

ности:

1) проводим прямые, перпендикулярные

C\D\, по которым будут перемещаться го-

ризонтальные проекции вращающихся то-

чек;

2) строим проекции радиуса вращения

одной из них, например А. Это будут от-

резки А\0\ и ЛгОг;

3) по двум проекциям определяем истин-

ную величину радиуса вращения RA• На

рис. 142 радиус RA определен вращением

отрезка OA вокруг оси, проходящей через

точку О и перпендикулярной плоскости Г1

;

4) отрезок RA откладываем от точки