Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

Для этого прежде всего проведем через

прямую а вспомогательную плоскость у.

Весьма удобно в качестве такой плоскости

воспользоваться одной из проецирующих

плоскостей. »

В данном случае через прямую а прове-

дена горизонтально проецирующая плос-

кость у, горизонтальный след которой сли-

вается с одноименной проекцией прямой.

Далее построены проекции п\ и «г линии

пересечения плоскостей, сравнение кото-

рых с проекциями данной прямой показы-

вает, что прямая а не параллельна плоско-

сти треугольника BCD.

§ 22. ПРЯМАЯ ЛИНИЯ,

ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ

Задача, которой посвящен настоящий

параграф, является одной из основных

задач начертательной геометрии. От того,

насколько хорошо она будет усвоена, за-

висит успешное изучение последующего

материала. Достаточно перечислить неко-

торые из задач курса, которые в конечном

счете сводятся к определению точки пе-

ресечения прямой линии и плоскости: пе-

ресечение прямой с многогранником, пе-

ресечение многогранника, конуса, цилинд-

ра и любой линейчатой поверхности

с плоскостью, пересечение двух многог-

ранников.

Согласно изложенной в § 20 методике

решения задачи на пересечение прямой

линии и плоскости необходимо различать

следующие три этапа:

I) построение вспомогательной плоско-

сти у, которую проводят через прямую

а (аеу);

2) построение линии пересечения п

вспомогательной плоскости у и заданной

а (п = aflv);

3) определение искомой точки К как

точки пересечения двух прямых: данной

а и построенной п (К = а(]п) (см. рис. 89).

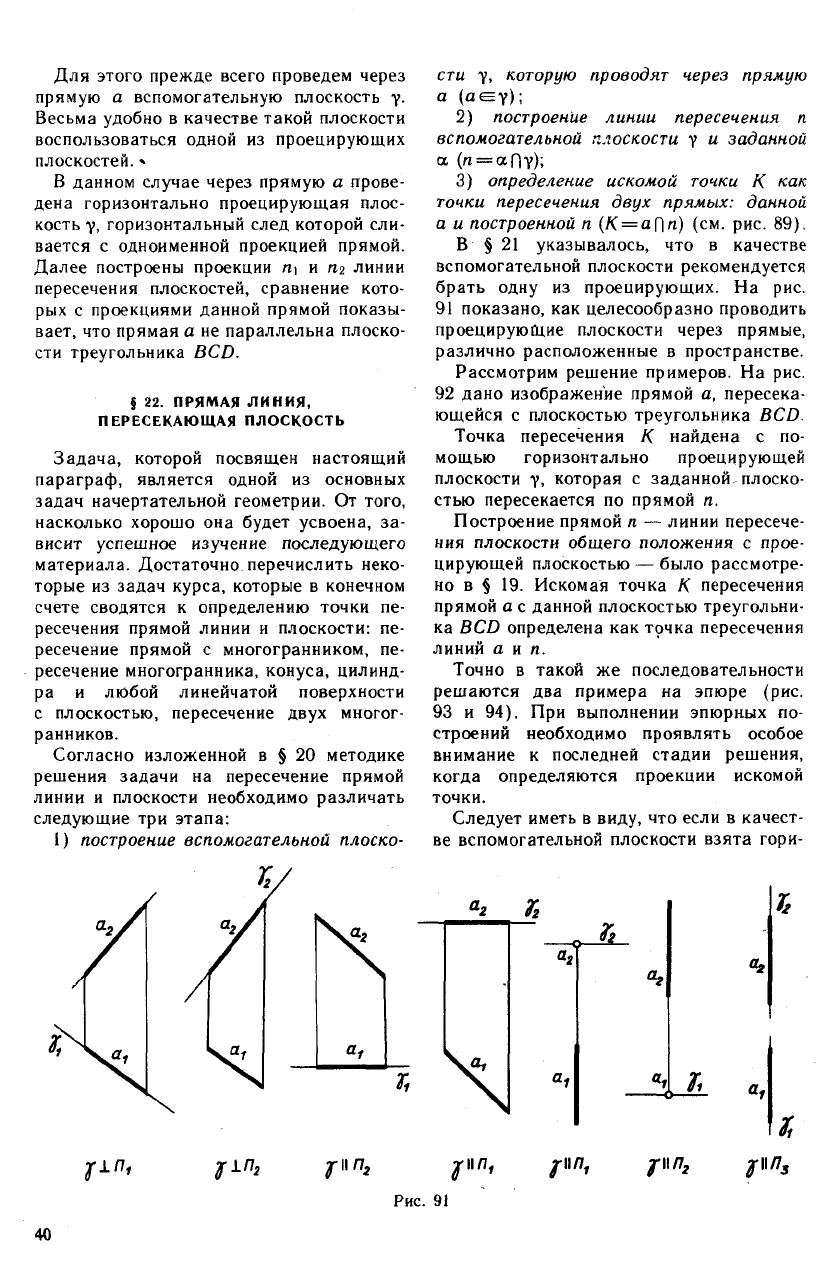
В § 21 указывалось, что в качестве

вспомогательной плоскости рекомендуется

брать одну из проецирующих. На рис.

91 показано, как целесообразно проводить

проецирующие плоскости через прямые,

различно расположенные в пространстве.

Рассмотрим решение примеров. На рис.

92 дано изображение прямой а, пересека-

ющейся с плоскостью треугольника BCD.

Точка пересечения К найдена с по-

мощью горизонтально проецирующей

плоскости у, которая с заданной, плоско-

стью пересекается по прямой п.

Построение прямой п — линии пересече-

ния плоскости общего положения с прое-

цирующей плоскостью — было рассмотре-

но в § 19. Искомая точка К пересечения

прямой а с данной плоскостью треугольни-

ка BCD определена как трчка пересечения

линий а и п.

Точно в такой же последовательности

решаются два примера на эпюре (рис.

93 и 94). При выполнении эпюрных по-

строений необходимо проявлять особое

внимание к последней стадии решения,

когда определяются проекции искомой

точки.

Следует иметь в виду, что если в качест-

ве вспомогательной плоскости взята гори-

J in, fin

jrll П

jtn, fin, р\п

р\п

Рис. 91

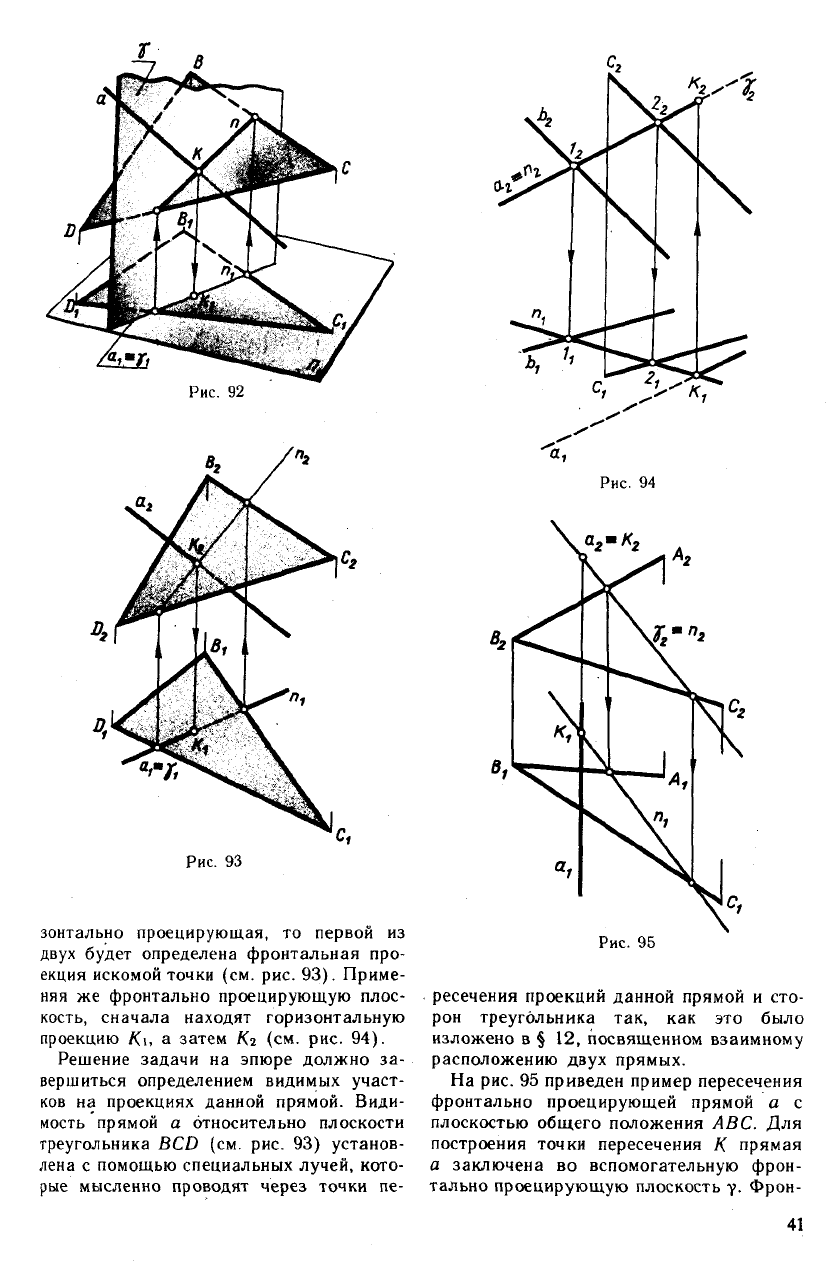
Рис. 92

Рис. 93

зонтально проецирующая, то первой из

двух будет определена фронтальная про-

екция искомой точки (см. рис. 93). Приме-

няя же фронтально проецирующую плос-

кость, сначала находят горизонтальную

проекцию К\, а затем Кг (см. рис. 94).

Решение задачи на эпюре должно за-

вершиться определением видимых участ-

ков на проекциях данной прямой. Види-

мость прямой а относительно плоскости

треугольника BCD (см. рис. 93) установ-

лена с помощью специальных лучей, кото-

рые мысленно проводят через точки пе-

Рис. 94

Рис. 95

ресечения проекций данной прямой и сто-

рон треугольника так, как это было

изложено в § 12, посвященном взаимному

расположению двух прямых.

На рис. 95 приведен пример пересечения

фронтально проецирующей прямой а с

плоскостью общего положения ABC. Для

построения точки пересечения К прямая

а заключена во вспомогательную фрон-

тально проецирующую плоскость у. Фрон-

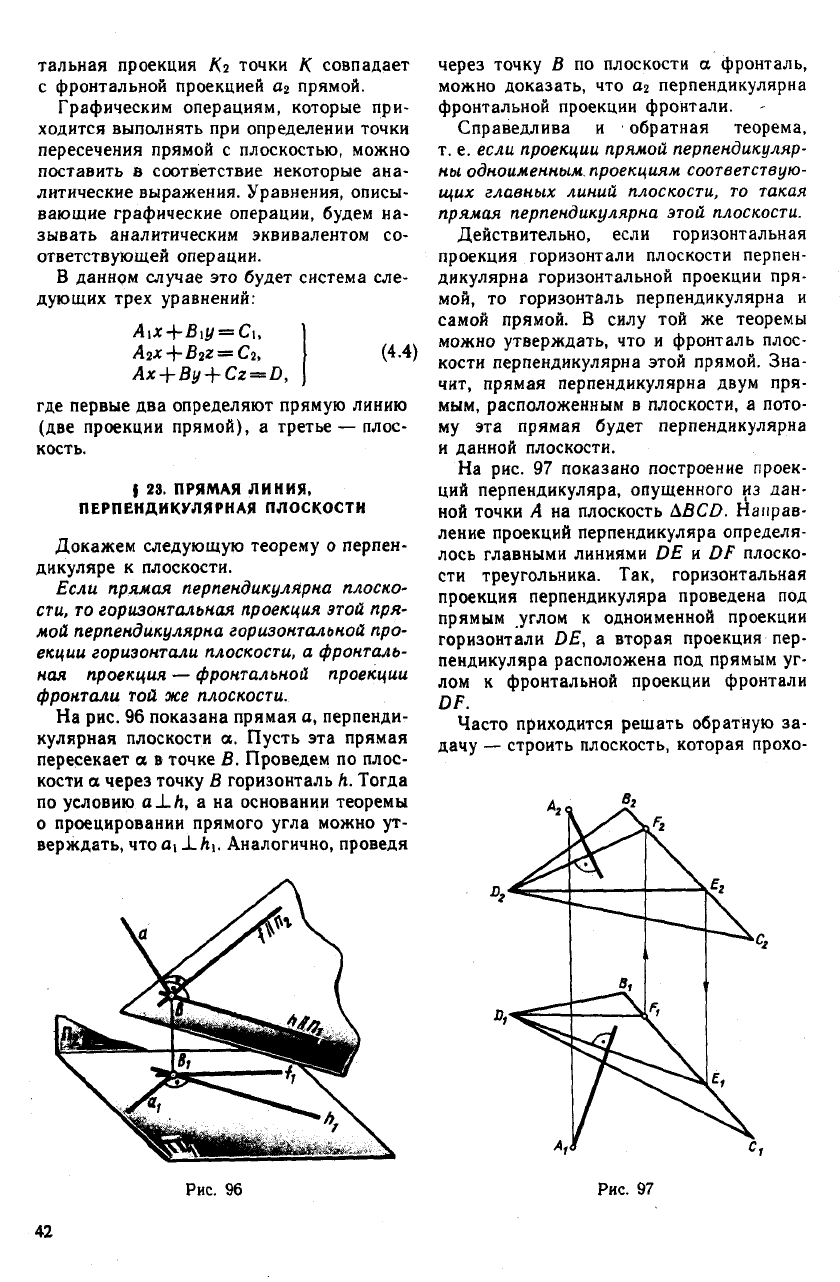
тальная проекция К.2 точки К совпадает

с фронтальной проекцией а

прямой.

Графическим операциям, которые при-

ходится выполнять при определении точки

пересечения прямой с плоскостью, можно

поставить в соответствие некоторые ана-

литические выражения. Уравнения, описы-

вающие графические операции, будем на-

зывать аналитическим эквивалентом со-

ответствующей операции.

В данном случае это будет система сле-

дующих трех уравнений:

А\х-\-В\у = С\,

Агх + В&^Сг,

Ax + By + Cz = D,

(4.4)

где первые два определяют прямую линию

(две проекции прямой), а третье — плос-

кость.

{ 23. ПРЯМАЯ ЛИНИЯ,

ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ

Докажем следующую теорему о перпен-

дикуляре к плоскости.

Если прямая перпендикулярна плоско-

сти, то горизонтальная проекция этой пря-

мой перпендикулярна горизонтальной про-

екции горизонтали плоскости, а фронталь-

ная проекция — фронтальной проекции

фронтали той же плоскости.

На рис. 96 показана прямая а, перпенди-

кулярная плоскости а. Пусть эта прямая

пересекает а в точке В. Проведем по плос-

кости а через точку В горизонталь А. Тогда

по условию a_LA, а на основании теоремы

о проецировании прямого угла можно ут-

верждать, что а

_L Ai.

Аналогично, проведя

через точку В по плоскости а фронталь,

можно доказать, что а

перпендикулярна

фронтальной проекции фронтали.

Справедлива и обратная теорема,

т. е. если проекции прямой перпендикуляр-

ны одноименным, проекциям соответствую-

щих главных линий плоскости, то такая

прямая перпендикулярна этой плоскости.

Действительно, если горизонтальная

проекция горизонтали плоскости перпен-

дикулярна горизонтальной проекции пря-

мой, то горизонталь перпендикулярна и

самой прямой. В силу той же теоремы

можно утверждать, что и фронталь плос-

кости перпендикулярна этой прямой. Зна-

чит, прямая перпендикулярна двум пря-

мым, расположенным в плоскости, а пото-

му эта прямая будет перпендикулярна

и данной плоскости.

На рис. 97 показано построение проек-

ций перпендикуляра, опущенного из дан-

ной точки А на плоскость ДBCD. Направ-

ление проекций перпендикуляра определя-

лось главными линиями DE и DF плоско-

сти треугольника. Так, горизонтальная

проекция перпендикуляра проведена под

прямым углом к одноименной проекции

горизонтали DE, а вторая проекция пер-

пендикуляра расположена под прямым уг-

лом к фронтальной проекции фронтали

DF.

Часто приходится решать обратную за-

дачу — строить плоскость, которая прохо-

Рис. 131

Рис. 132 Рис. 133

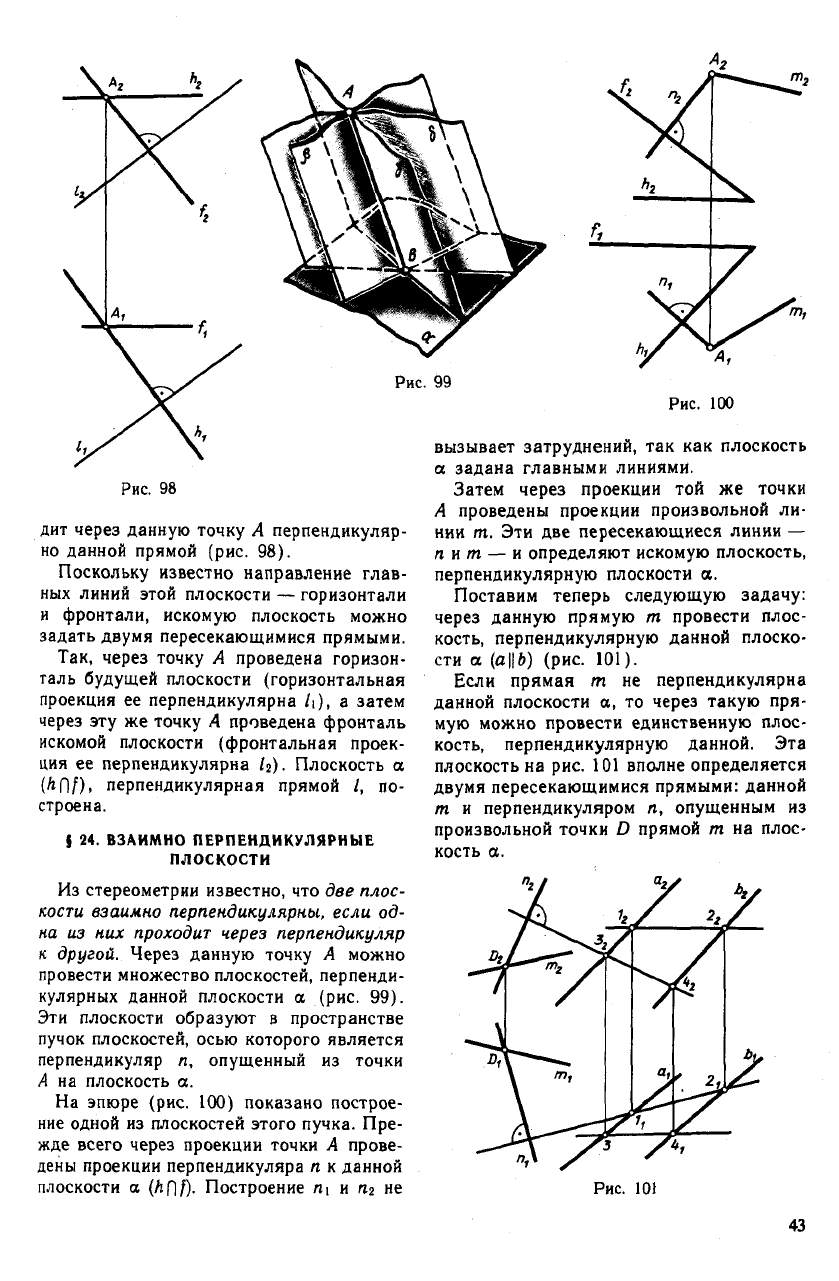
Рис. 99

Рис. 98

дит через данную точку А перпендикуляр-

но данной прямой (рис. 98).

Поскольку известно направление глав-

ных линий этой плоскости — горизонтали

и фронтали, искомую плоскость можно

задать двумя пересекающимися прямыми.

Так, через точку А проведена горизон-

таль будущей плоскости (горизонтальная

проекция ее перпендикулярна U), а затем

через эту же точку А проведена фронталь

искомой плоскости (фронтальная проек-

ция ее перпендикулярна /

). Плоскость а

{h[)f), перпендикулярная прямой /, по-

строена.

{ 24. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ

ПЛОСКОСТИ

Из стереометрии известно, что две плос-

кости взаимно перпендикулярны, если од-

на из них проходит через перпендикуляр

к другой. Через данную точку А можно

провести множество плоскостей, перпенди-

кулярных данной плоскости а (рис. 99).

Эти плоскости образуют в пространстве

пучок плоскостей, осью которого является

перпендикуляр л, опущенный из точки

А на плоскость а.

На эпюре (рис. 100) показано построе-

ние одной из плоскостей этого пучка. Пре-

жде всего через проекции точки А прове-

дены проекции перпендикуляра п к данной

плоскости a

(hf]f).

Построение ni и пг не

Рис. 100

вызывает затруднений, так как плоскость

ос задана главными линиями.

Затем через проекции той же точки

А проведены проекции произвольной ли-

нии т. Эти две пересекающиеся линии —

пит — и определяют искомую плоскость,

перпендикулярную плоскости а.

Поставим теперь следующую задачу:

через данную прямую т провести плос-

кость, перпендикулярную данной плоско-

сти а (а ||

ft)

(рис. 101).

Если прямая m не перпендикулярна

данной плоскости а, то через такую пря-

мую можно провести единственную плос-

кость, перпендикулярную данной. Эта

плоскость на рис. 101 вполне определяется

двумя пересекающимися прямыми: данной

т и перпендикуляром п, опущенным из

произвольной точки D прямой т на плос-

кость а.

Используя признак взаимно перпенди-

кулярных плоскостей, можно, не опреде-

ляя двугранного угла между ними, сде-

лать вывод о том, перпендикулярны плос-

кости друг другу или нет.

Пусть даны две плоскости a (Af|/)

(ABC) (рис. 102). Требуется установить,

перпендикулярны ли они друг другу. Для

этого на одной из них (на плоскости р)

взята произвольная точка А, через кото-

рую проведена прямая п, перпендикуляр-

ная другой плоскости а. Остается устано-

вить относительное положение п и плоско-

сти р. Если п лежит в плоскости р, то PJL

.La, в противном случае данные плоско-

сти не перпендикулярны. На рис. 102 вид-

но, что прямая п не принадлежит

плоскости р (ABC). Следовательно, плос-

кости а и р не перпендикулярны друг

другу.

Вопросы и задачи для самоконтроля

1. При каком положении плоскости ее гори-

зонталь является и профильной прямой?

2. Какая из главных линий плоскости опреде-

ляет ее положение в пространстве?

3. В каком случае фронталь плоскости

является одновременно и линией наибольшего

уклона?

4. В каких пределах может изменяться уклон

прямой, принадлежащей плоскости, если эта

плоскость образует с плоскостью Пi угол

<р

= 45°?

5. Сколько вершин можно задать произволь-

но при построении проекций параллелограмма,

ромба, квадрата?

6. При каком условии ортогональная проек-

ция квадрата может быть ромбом?

7. Как построить прямую, параллельную двум

пересекающимся плоскостям?

8. Сколько плоскостей симметрии имеет одна

плоскость?

9. Назовите основное свойство проецирующих

плоскостей.

10. Построить плоскость, проходящую через

прямую I и перпендикулярную данной плоскости

общего положения.

11. При каком условии проекция биссектрисы

угла является биссектрисой проекции того же

угла?

12. Даны две скрещивающиеся прямые обще-

го положения. Требуется построить плоскость,

равноудаленную от каждой из них.

13. Решение каких задач начертательной гео-

метрии требует многократного определения то-

чек пересечения прямой с плоскостью? Назовите

три основных этапа выполнения этой задачи.

14. Какой вид имеет уравнение плоскости,

проходящей через начало координат? Как по-

строить следы такой плоскости?

ГЛАВА 5

МНОГОГРАННИКИ

§ 25. СПОСОБЫ ЗАДАНИЯ МНОГОГРАННИКОВ

И ПОСТРОЕНИЕ ИХ ПРОЕКЦИЯ

Многогранником называется совокуп-

ность таких плоских многоугольников, у

которых каждая сторона одного является

одновременно стороной другого (но только

одного).

Предметом нашего изучения будут толь-

ко выпуклые многогранники, т. е. такие,

которые расположены по одну сторону

каждой его грани.

Форма и положение многогранника в

пространстве могут быть определены зада-

нием его ребер, основанием и вершиной,

если это пирамида, основанием и одним из

боковых ребер, если это призма.

Существует и аналитическое задание

многогранника системой линейных нера-

венств с тремя неизвестными:

a\X

+ b

y + c

z^td

x + b

y + c

z^d

, ^ jj

anX-\-b^ + c

z^d„.

Каждому из неравенств в трехмерном

пространстве соответствует полупростран-

ство с граничной плоскостью, уравнение

которой получится, если знак неравенства

заменить знаком равенства.

Область, определяемая системой (5.1),

представляет собой пересечение п полуп-

ространств. Так как каждое полупро-

странство есть выпуклая область, то их

пересечение окажется также выпуклой об-

ластью.

Итак, любой выпуклый многогранник

можно получить пересечением конечного

числа полупространств.

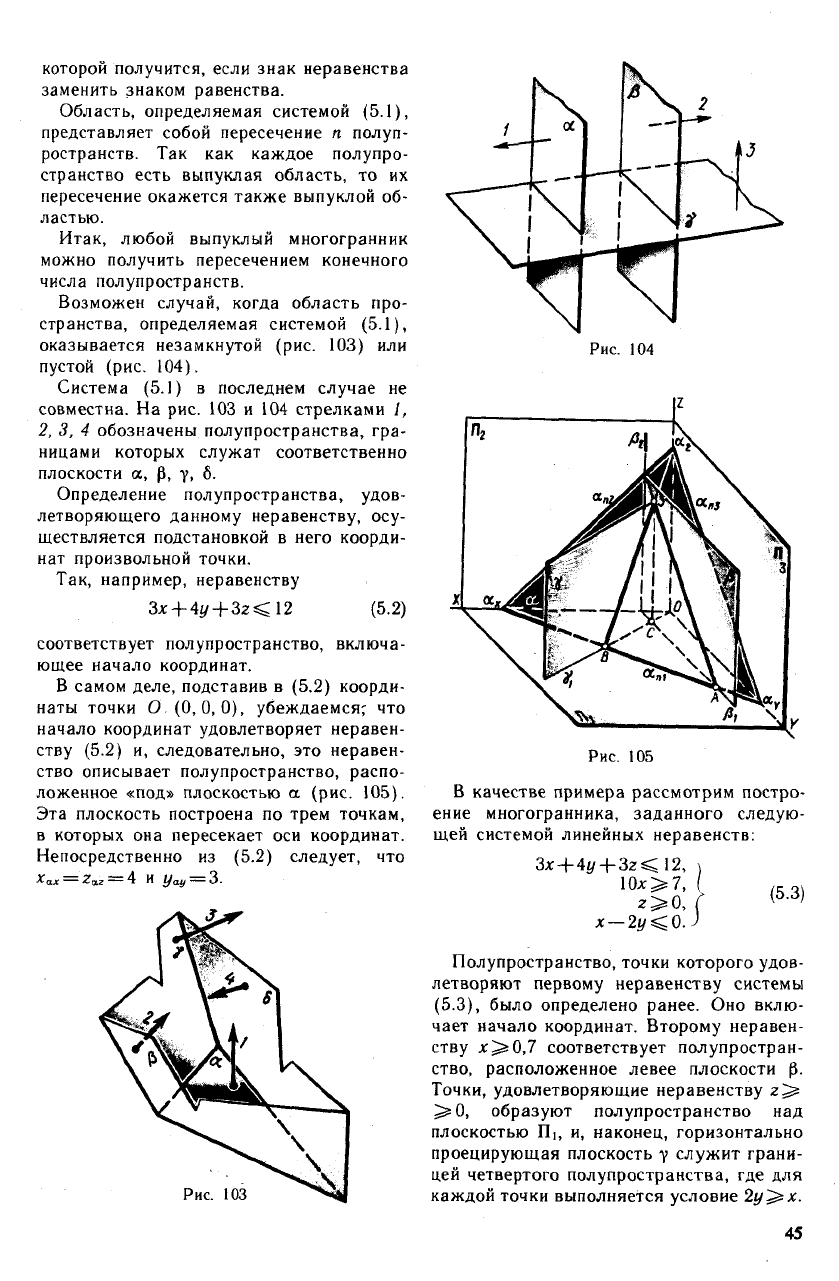
Возможен случай, когда область про-

странства, определяемая системой (5.1),

оказывается незамкнутой (рис. 103) или

пустой (рис. 104).

Система (5.1) в последнем случае не

совместна. На рис. 103 и 104 стрелками 1,

2, 3, 4 обозначены полупространства, гра-

ницами которых служат соответственно

плоскости а, р, у, 6.

Определение полупространства, удов-

летворяющего данному неравенству, осу-

ществляется подстановкой в него коорди-

нат произвольной точки.

Так, например, неравенству

3х + 4у + 32<12

(5.2)

соответствует полупространство, включа-

ющее начало координат.

В самом деле, подставив в (5.2) коорди-

наты точки О (0,0,0), убеждаемся; что

начало координат удовлетворяет неравен-

ству (5.2) и, следовательно, это неравен-

ство описывает полупространство, распо-

ложенное «под» плоскостью а (рис. 105).

Эта плоскость построена по трем точкам,

в которых она пересекает оси координат.

Непосредственно из (5.2) следует, что

АХ

ZRXZ

===

4 И УАУ^

Рис. 104

Рис. 105

В качестве примера рассмотрим постро-

ение многогранника, заданного следую-

щей системой линейных неравенств:

3x + 4(/ + 3z< 12,

10* >7,

х — 2t/<0J

(5.3)

Рис. 103

Полупространство, точки которого удов-

летворяют первому неравенству системы

(5.3), было определено ранее. Оно вклю-

чает начало координат. Второму неравен-

ству х>0,7 соответствует полупростран-

ство, расположенное левее плоскости р.

Точки, удовлетворяющие неравенству z^

^0, образуют полупространство над

плоскостью П1, и, наконец, горизонтально

проецирующая плоскость у служит грани-

цей четвертого полупространства, где для

каждой точки выполняется условие 2у^х.

Следующий шаг решения задачи заклю-

чается в построении линий пересечения

плоскостей-границ полупространств.

Так, на рис. 105 АВ=a(]Th, AC = $[}Ih,

ВС = уПП|, i4S = aflP, BS = aflY. CS =

= РП?; попарно пересекаясь, эти прямые

определяют вершины тетраэдра.

Его ортогональные проекции показаны

на рис. 106.

Заметим, что замкнутая многогранная

область, представляющая собой пересече-

ние конечного числа полупространств, на-

зывается многогранником решений систе-

мы линейных неравенств.

Координаты точек, расположенных

внутри и на гранях этого многогранника,

удовлетворяют той системе линейных не-

равенств, которыми определен данный

многогранник.

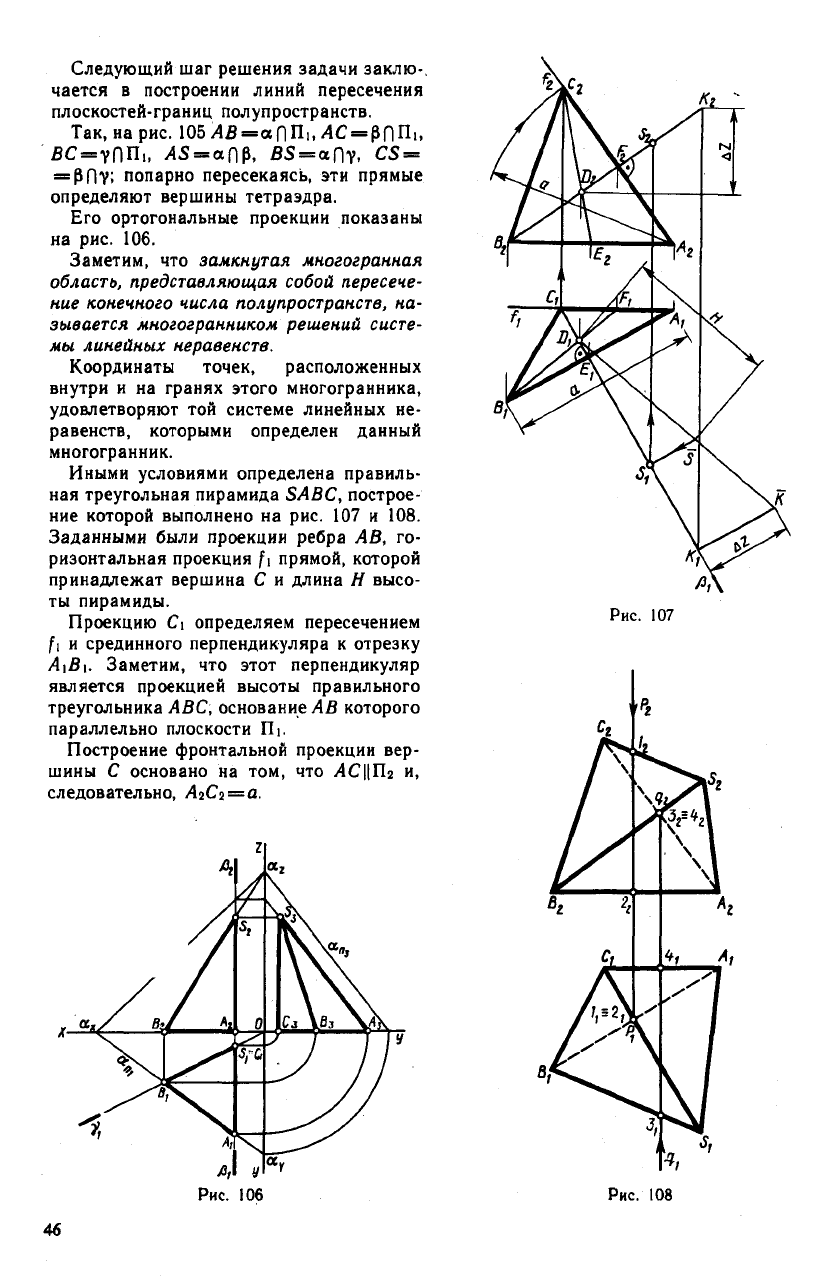
Иными условиями определена правиль-

ная треугольная пирамида SABC, построе-

ние которой выполнено на рис. 107 и 108.

Заданными были проекции ребра АВ, го-

ризонтальная проекция f

прямой, которой

принадлежат вершина С и длина Н высо-

ты пирамиды.

Проекцию С1 определяем пересечением

f 1 и срединного перпендикуляра к отрезку

А\В\. Заметим, что этот перпендикуляр

является проекцией высоты правильного

треугольника ABC, основание АВ которого

параллельно плоскости Пь

Построение фронтальной проекции вер-

шины С основано на том, что /4С||Пг и,

следовательно, АгСг = а.

CJ \вз \)к

SfG

J J I У

А,

Рис.

131

Рис. 132 Рис. 133

Определение вершины S потребовало

построения перпендикуляра DK к плоско-

сти основания, проходящего через центр

D треугольника ABC. Этот центр найден

пересечением медиан СЕ и BF. Далее, на

прямой DK отложе"н отрезок DS, равный

высоте Н пирамиды. Положение точки

S отрезка DS определяется из условия, что

£>iS D\K

(5.4)

где D

S=H, D

K— истинная длина от-

резка DK, найденная с помощью прямоу-

гольного треугольника D\K\K. Остается

соединить полученные вершины пирамиды

и установить видимость пересекающихся

проекций ребер, оказавшихся внутри кон-

тура каждой проекции многогранника.

Для этой цели воспользуемся проецирую-

щими лучами р_1-П| и ql. Пг.

Первый из них проходит через точку

(/i=2i) пересечения горизонтальных про-

екций ребер SC и АВ, а второй — через

точку (32 — 4

) пересечения S2B2 и Л

Сг.

Замечая, что zi>z

и уз>у*, решаем

вопрос о видимости ребер при виде сверху

и спереди.

этой точки. Аналогичные построения, свя-

занные с поиском точек 2 и 3, на эпюре не

показаны.

Решение задачи существенно упрощает-

ся, если секущая плоскость перпендику-

лярна одной из плоскостей проекций.

В этом случае (рис. 110, где a-Lib) одна

из проекций сечения вырождается в пря-

мую линию, совпадающую со следом прое-

цирующей плоскости (см. точки

= S

na2, 2

=А2В

(]а

, ...,

= S

Па*)-

§ 26. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТИ И ПРЯМОЙ

ЛИНИИ С МНОГОГРАННИКОМ

Построение сечения многогранника тре-

бует многократного решения задачи о пе-

ресечении прямой с плоскостью. Точки,

в которых ребра многогранника пересека-

ются с заданной плоскостью, будут верши-

нами искомого сечения.

Тот же результат можно получить, све-

дя задачу к построению прямых пересече-

ния плоскости с гранями тела.

На рис. 109 показано сечение треуголь-

ной призмы плоскостью а(аП6). Каждая

из вершин построенного треугольника

(12 3) определена как точка пересечения

соответствующего ребра с заданной плос-

костью а. Так, точка 1=АА

По. Вспомо-

гательная горизонтально проецирующая

плоскость у, проведенная через ребро АА

[

пересекает плоскость а по прямой ММ.

Построив M

Nt, определяем /2 = М

#2П

n-42i4j, а затем с помощью линии проекци-

онной связи находим вторую проекцию 1\

Рис. 110

Ниже (см. § 30, 32) будет показана

возможность преобразования секущей

плоскости общего положения в проециру-

ющую — преобразования, позволяющего

получить решение, которое не перегруже-

но обилием накладывающихся одно на

другое построений.

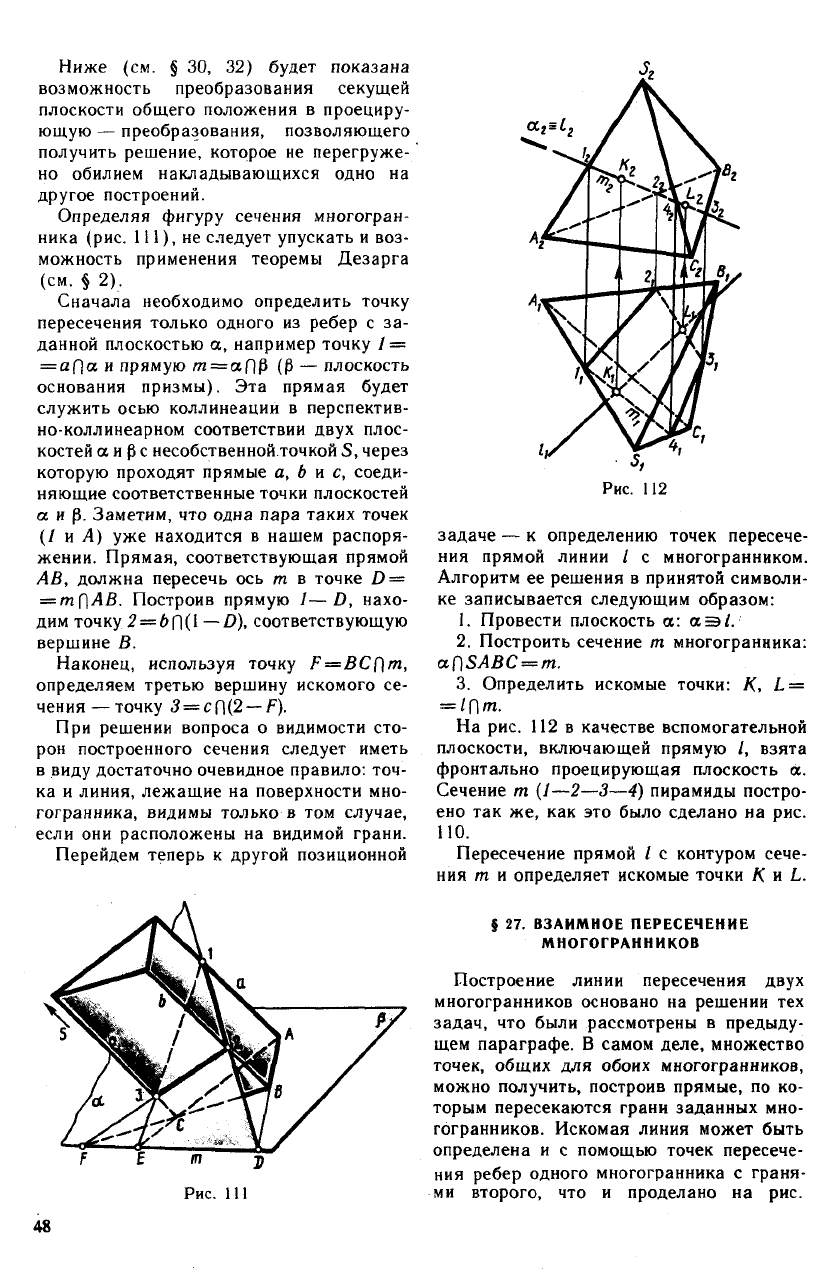
Определяя фигуру сечения многогран-

ника (рис. 111), не следует упускать и воз-

можность применения теоремы Дезарга

(см. § 2).

Сначала необходимо определить точку

пересечения только одного из ребер с за-

данной плоскостью а, например точку

—

= а[}а и прямую m = af)Р (Р — плоскость

основания призмы). Эта прямая будет

служить осью коллинеации в перспектив-

но-коллинеарном соответствии двух плос-

костей аире несобственнойточкой S, через

которую проходят прямые а, b и с, соеди-

няющие соответственные точки плоскостей

аир. Заметим, что одна пара таких точек

(/ и А) уже находится в нашем распоря-

жении. Прямая, соответствующая прямой

АВ, должна пересечь ось т в точке D =

= т[\АВ. Построив прямую 1—D, нахо-

дим точку 2 = 6f|(l—D), соответствующую

вершине В.

Наконец, используя точку F=BCf)m,

определяем третью вершину искомого се-

чения — точку 3 — сП(2 — F).

При решении вопроса о видимости сто-

рон построенного сечения следует иметь

в виду достаточно очевидное правило: точ-

ка и линия, лежащие на поверхности мно-

гогранника, видимы только в том случае,

если они расположены на видимой грани.

Перейдем теперь к другой позиционной

Рис. 111

задаче — к определению точек пересече-

ния прямой линии / с многогранником.

Алгоритм ее решения в принятой символи-

ке записывается следующим образом:

1. Провести плоскость а: аэ/.

2. Построить сечение т многогранника:

a(]SABC = m.

3. Определить искомые точки: К, L =

— 1[\т.

На рис. 112 в качестве вспомогательной

плоскости, включающей прямую /, взята

фронтально проецирующая плоскость а.

Сечение т (1—2—3—4) пирамиды постро-

ено так же, как это было сделано на рис.

110.

Пересечение прямой I с контуром сече-

ния т и определяет искомые точки К и L.

$ 27. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ

МНОГОГРАННИКОВ

Построение линии пересечения двух

многогранников основано на решении тех

задач, что были рассмотрены в предыду-

щем параграфе. В самом деле, множество

точек, общих для обоих многогранников,

можно получить, построив прямые, по ко-

торым пересекаются грани заданных мно-

гогранников. Искомая линия может быть

определена и с помощью точек пересече-

ния ребер одного многогранника с граня-

ми второго, что и проделано на рис.

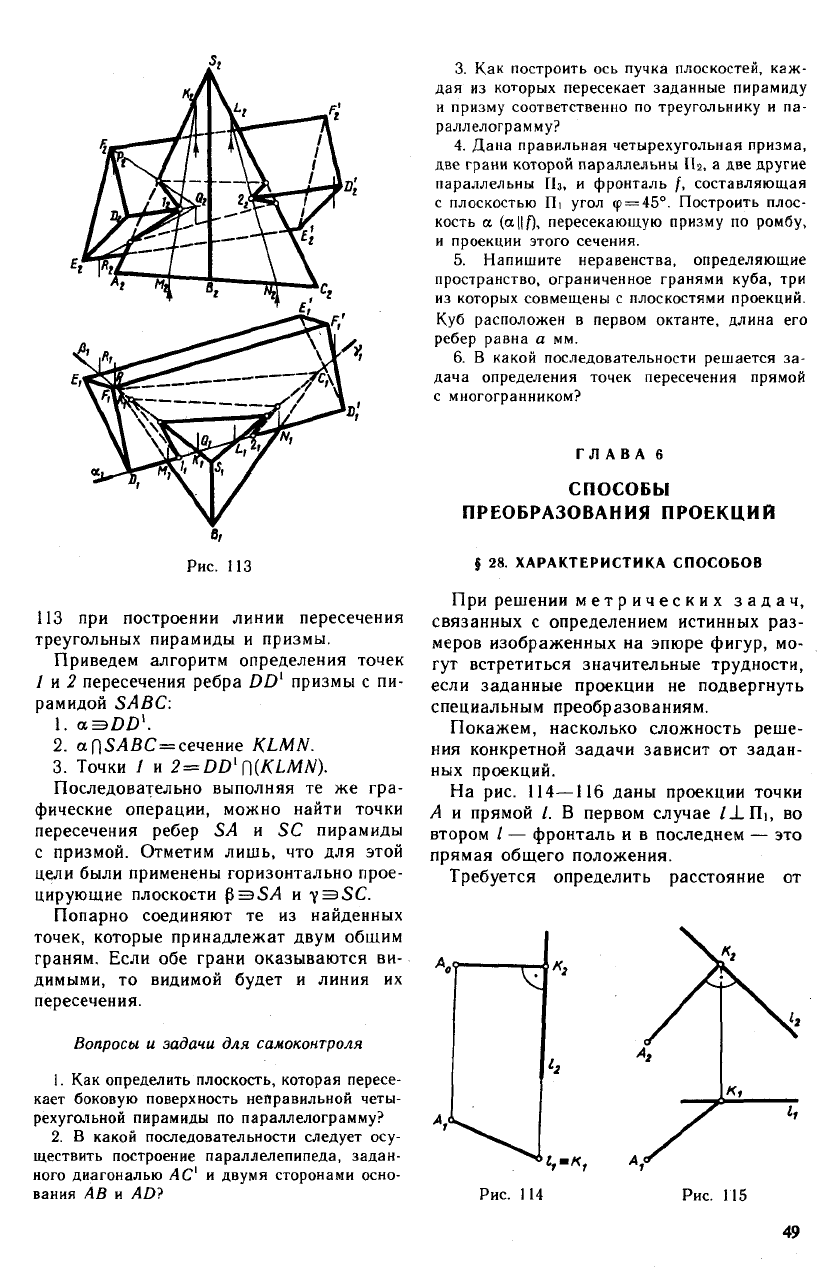
113 при построении линии пересечения

треугольных пирамиды и призмы.

Приведем алгоритм определения точек

/ и 2 пересечения ребра DD

[

призмы с пи-

рамидой SABC:

1. aESDD\

2. а nS/lBC = сечение KLMN.

3. Точки / и 2 = DD

[\{KLMN).

Последовательно выполняя те же гра-

фические операции, можно найти точки

пересечения ребер S/1 и SC пирамиды

с призмой. Отметим лишь, что для этой

цели были применены горизонтально прое-

цирующие плоскости и уз SC.

Попарно соединяют те из найденных

точек, которые принадлежат двум общим

граням. Если обе грани оказываются ви-

димыми, то видимой будет и линия их

пересечения.

Вопросы и задачи для самоконтроля

1. Как определить плоскость, которая пересе-

кает боковую поверхность неправильной четы-

рехугольной пирамиды по параллелограмму?

2. В какой последовательности следует осу-

ществить построение параллелепипеда, задан-

ного диагональю А С' и двумя сторонами осно-

вания АВ и AD?

3. Как построить ось пучка плоскостей, каж-

дая из которых пересекает заданные пирамиду

и призму соответственно по треугольнику и па-

раллелограмму?

4. Дана правильная четырехугольная призма,

две грани которой параллельны 1Ъ, а две другие

параллельны Пз, и фронталь f, составляющая

с плоскостью П| угол

<р

= 45°. Построить плос-

кость а

(а|| f),

пересекающую призму по ромбу,

и проекции этого сечения.

5. Напишите неравенства, определяющие

пространство, ограниченное гранями куба, три

из которых совмещены с плоскостями проекций.

Куб расположен в первом октанте, длина его

ребер равна а мм.

6. В какой последовательности решается за-

дача определения точек пересечения прямой

с многогранником?

ГЛАВА 6

СПОСОБЫ

ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

§ 28. ХАРАКТЕРИСТИКА СПОСОБОВ

При решении метрических задач,

связанных с определением истинных раз-

меров изображенных на эпюре фигур, мо-

гут встретиться значительные трудности,

если заданные проекции не подвергнуть

специальным преобразованиям.

Покажем, насколько сложность реше-

ния конкретной задачи зависит от задан-

ных проекций.

На рис. 114—116 даны проекции точки

А и прямой I. В первом случае / J_ П1, во

втором / — фронталь и в последнем — это

прямая общего положения.

Требуется определить расстояние от

Рис. 114