Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

7. Проведены проекции горизонтали, на

которой находится вершина А: фронталь-

ная проекция — через 3

, горизонталь-

ная — через 3].

8. Через точку А

(горизонтальную про-

екцию вершины в повернутом положении)

проведена прямая, перпендикулярная hi.

По этой прямой будет перемещаться гори-

зонтальная проекция А! точки А при об-

ратном вращении плоскости. Горизонталь-

ная проекйия А> вершины А (после обрат-

ного поворота) будет получена в пересече-

нии прямой, перпендикулярной hi, с ранее

проведенной проекцией горизонтали.

9. В проекционной связи на фронталь-

ной проекции горизонтали, проходящей

через точку 3

, находим точку А

Таким же образом определяются проек-

ции и других вершин треугольника ABC.

В относительно громоздком построении

главное заключалось в том, что через каж-

дую вершину треугольника по плоскости,

повернутой до положения уровня, прово-

дили прямые линии — горизонтали плос-

кости а, с вращения которых и начинали

процесс обратного поворота плоскости.

Первый этап этого поворота завершали

построением проекций горизонталей, а в

результате второго этапа на заранее под-

готовленных проекциях прямых определя-

ли проекции вершин заданной плоской

фигуры.

f 36. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К РЕШЕНИЮ КОНСТРУКТИВНЫХ ЗАДАЧ

Конструктивными задачами

принято называть задачи на построение

геометрических фигур, отвечающих напе-

ред заданным условиям.

Значительную часть конструктивных за-

дач удается решить методом «пересече-

ния множеств», содержание которого

в общем виде можно описать следующим

образом.

Пусть искомое множество точек М (не-

которая геометрическая фигура) должно

отвечать ряду условий, ряду характери-

стических свойств, которым должны обла-

дать элементы этого множества.

Тогда прежде всего необходимо рас-

членить поставленное требование зада-

чи на отдельные части, на отдельные усло-

вия.

Далее следует последовательно опреде-

лить те множества Mi, М

, ..., М

, каждое

из которых удовлетворяет соответствую-

щему условию или отдельной группе усло-

вий и отвечает требуемым характеристиче-

ским свойствам.

Наконец, остается определить те и толь-

ко те элементы, которые принадлежат од-

новременно каждому из найденных мно-

жеств Mi, М

, ..., М„, т. е. определить их

пересечение (подмножество, являю-

щееся общей частью множеств).

Графические построения в ряде случаев

могут быть упрощены, если проекции неко-

торых из заданных геометрических фигур

подвергнуть специальному преобразова-

нию, повторяющему решение одной из че-

тырех основных задач, рассмотренных вы-

ше. Покажем целесообразность таких пре-

образований на конкретных примерах.

Пример 1. На прямой а определить точ-

ки, удаленные от плоскости a (/if|/) на

расстояние п мм (рис. 167).

Множество точек Mi, отвечающих пер-

вому условию, уже задано — это сама

прямая а.

Второму условию будут удовлетворять

точки двух плоскостей Р и v. параллельных

а и удаленных от а на п мм. Точки этих

плоскостей являются вторым множеством

. Пересечение Mi и М

даст искомый

результат.

Переход от системы плоскостей П2/П1

к П4/П1 был осуществлен с таким расче-

том, чтобы в новой системе П4/П1 плос-

кость а стала проецирующей (а±П

Напомним, что для этого необходимо обес-

печить ортогональнось плоскости П

и го-

ризонтали h плоскости а (П4ХЛ). Рассто-

яние п между параллельными плоскостями

на II4 спроецируется без искажения, что

и позволило без дополнительных построе-

ний провести следы р

и Y4 плоскостей р

и у.

Искомые точки обозначены через

К (К = аПР) и L (L = a[)y).

Пример 2. Построить прямую т, равно-

удаленную от трех параллельных прямых

общего положения а, Ь, с, не лежащих

в одной плоскости (рис. 168).

Искомая прямая должна быть такой,

чтобы для ее произвольной точки К выпол-

нялось равенство трех расстояний КА =

= KB = КС.

Расчленим требование задачи на два

следующих условия. Первое — КА = КВ.

Второе — КВ = КС. Будем удовлетворять

каждому условию порознь. Множество М\

прямых, отвечающих только первому усло-

вию, образует плоскость а, перпендику-

лярную отрезку АВ (/4еа, fiei, АВ±.а,

АВ±6) и проходящую через его середину.

Второму условию соответствует аналогич-

ная плоскость P-LBC (Сес, ВС±Ь, ВСJ.

_Lc). Пересечение двух плоскостей (двух

множеств) определяет искомую прямую

= а ПР- Отметим, что линия т может

рассматриваться как ось цилиндра враще-

ния, образующими которого служат за-

данные прямые.

Построения на эпюре окажутся менее

громоздкими, если перейти к новой систе-

ме плоскостей проекций, в которой прямые

а, Ь и с будут проецирующими. Центр

окружности, описанной около трех точек

(проекций заданных прямых на плоскость

Рис. 258

115, им перпендикулярную), будет ортого-

нальной проекцией на ту же плоскость

искомой прямой т.

Вопросы и задачи для самоконтроля

1. Какими будут проекции траектории точки,

вращающейся вокруг оси х?

2. По трем положениям вращающейся точки

определить ось i, около которой вращается

точка.

3. Даны прямая I и параллельная ей плос-

кость а. Каким должно быть положение оси,

вращением вокруг которой прямую I можно

совместить с плоскостью а?

4. Как следует расположить новую плоскость

проекций, чтобы определить расстояние между

двумя параллельными фронталями?

5. Каким должно быть положение оси враще-

ния при преобразовании плоскости общего по-

ложения в горизонтально проецирующую?

6. Что представляет собой множество точек,

равноудаленных отдвух пересекающихся плос-

костей? Как построить это множество точек,

пользуясь способом замены плоскостей проек-

ций?

ГЛАВА 7

КРИВЫЕ ЛИНИИ

Точку, прямую и плоскость называют

элементарными геометрическими фигура-

ми в том смысле, что из них могут быть

созданы все остальные геометрические фи-

гуры.

Приняв в качестве элементарной фигу-

ры точку, любую линию можно рассматри-

вать как множество последовательных по-

ложений движущейся точки — траекто-

рию точки.

Примером такой кривой может служить

циклоида — траектория точки окружно-

сти, катящейся без скольжения по прямой.

Эта кривая состоит из ряда «арок», каж-

дая из которых соответствует полному

обороту окружности (рис. 169).

В некоторых случаях линию удается

определить как множество точек, облада-

ющих каким-либо общим для всех них

свойством.

Так, лемниската Бернулли определяется

как множество точек плоскости, для кото-

рых произведение расстояний до двух то-

чек F| и F2 той же плоскости есть величина

постоянная, равная с

, т. е. MF\-MFi = c

(рис. 170).

Если же за элементарную фигуру при-

нята прямая, то всякую линию можно

рассматривать как огибающую своих ка-

сательных.

Точки кривой линии могут определяться

и законом своего движения. В механике

уравнения движения точки в координат-

ной форме имеют вид

* = /|(0. у = №, г = Ш- (7.1)

Давая параметру t различные значения,

определяют координаты движущейся точ-

ки и таким образом находят ее положение

в пространстве. Множество всех этих то-

чек образует некоторую линию, парамет-

рическими уравнениями которой являются

уравнения движения точки.

Задание кривой линии уравнениями

(7.1) вполне равносильно заданию кривой

вектор-функцией одного скалярного аргу-

мента t в определенной области изменения

последнего:

г = г"(/), Г

</<Г. (7.2)

Каждому значению t ставится в соответст-

вие вектор r(i)—OM, который откладыва

ют от некоторой фиксированной точки

О пространства (рис. 171). При изменении

параметра t точка М описывает в про-

странстве кривую пг.

Вектор-функция (7.2) может быть пред-

ставлена в виде

r(t) = x(t)i + y(t)i +

(t)k, (7.3)

где через x(t), y(t) и z(t) обозначены коорди-

наты вектора r(t).

В аналитической геометрии известны

и другие способы задания кривых.

Не всякую линию удается выразить в

аналитической форме. Тогда ее задают

графически на чертеже.

Графически — своим изображением мо-

жет быть задана и закономерная линия,

образование которой подчинено опреде-

ленным геометрическим условиям.

В начертательной геометрии кривые

линии изучаются по их проек-

циям. Построение проекций линий су-

щественно зависит прежде всего от того,

принадлежат ли все точки данной кривой

одной плоскости или нет. Если все точки

кривой расположены в одной плоскости, то

такая кривая называется плоской. При-

мером плоских кривых являются окруж-

ность, эллипс, парабола, гипербола, цик-

лоида и др.

Кривая линия, которая не может быть

совмещена с плоскостью всеми своими

точками, называется пространствен-

ной (линией двоякой кривизны).

Примером таких кривых служат винто-

вые линии, имеющие большое применение

в технике.

Укажем некоторые свойства проекций

плоских и пространственных кривых.

Так, если точка А принадлежит кривой

m (рис. 172), то проекция А\ этой точки

принадлежит проекции mi кривой.

Секущая и касательная к кривой прое-

цируются соответственно в секущую и ка-

сательную к проекции кривой.

Пусть через точку А кривой пг проведе-

на секущая п (рис. 172). Проекция секу-

шей определяется точками А

и Вi, при-

надлежащими проекции т\ рассматривае-

мой кривой. Прямая п\, пересекая проек-

цию кривой, является по отношению к т\

секущей.

Касательную / можно рассматривать

как предельное положение секущей, кото-

рое занимает последняя при сближении

точек пересечения Л и В до слияния их

в одну точку Л. В этом случае совпадут

друг с другом и их проекции, т. е. проек-

ция секущей превратится в касательную t\

к проекции тi кривой.

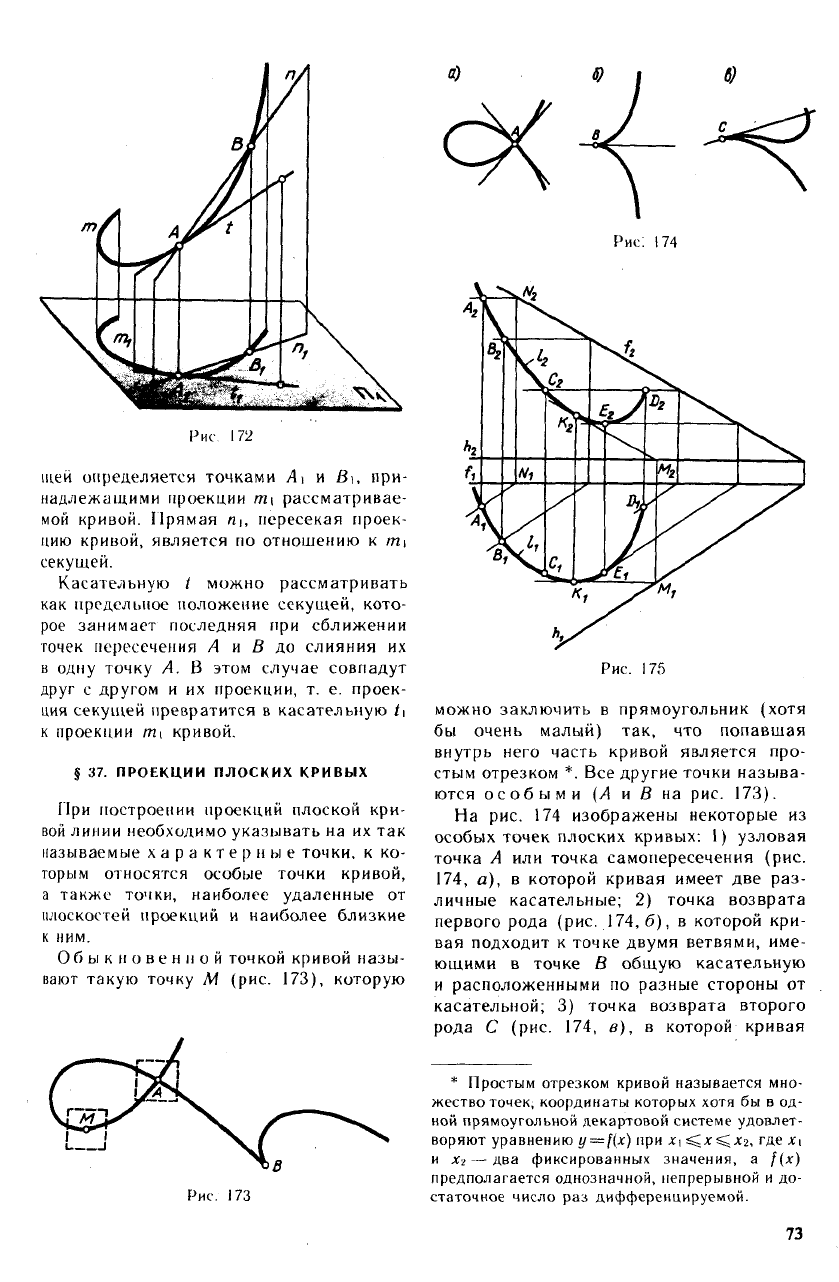
§ 37. ПРОЕКЦИИ ПЛОСКИХ КРИВЫХ

При построении проекций плоской кри-

вой линии необходимо указывать на их так

называемые характерные точки, к ко-

торым относятся особые точки кривой,

а также точки, наиболее удаленные от

плоскостей проекций и наиболее близкие

к ним.

О б ы к н о венной точкой кривой назы-

вают такую точку М (рис. 173), которую

Рис. 258

можно заключить в прямоугольник (хотя

бы очень малый) так, что попавшая

внутрь него часть кривой является про-

стым отрезком *. Все другие точки называ-

ются особыми (Л и В на рис. 173).

На рис. 174 изображены некоторые из

особых точек плоских кривых: 1) узловая

точка Л или точка самопересечения (рис.

174, а), в которой кривая имеет две раз-

личные касательные; 2) точка возврата

первого рода (рис. 174, б), в которой кри-

вая подходит к точке двумя ветвями, име-

ющими в точке В общую касательную

и расположенными по разные стороны от

касательной; 3) точка возврата второго

рода С (рис. 174, в), в которой кривая

* Простым отрезком кривой называется мно-

жество точек, координаты которых хотя бы в од-

ной прямоугольной декартовой системе удовлет-

воряют уравнению у —f(x) при

Х\

^.х^лгг, где Xi

и Xi — два фиксированных значения, а Цх)

предполагается однозначной, непрерывной и до-

статочное число раз дифференцируемой.

подходит к точке двумя ветвями, имеющи-

ми в точке С общую касательную, распо-

ложенную (вблизи точки С) по одну сто-

рону от обеих ветвей кривой.

На рис. 175 показано, как по заданной

фронтальной проекции /

линии /, принад-

лежащей плоскости а (Л(1/). может быть

построена ее вторая (горизонтальная 1\)

проекция.

В основе выполненного построения ле-

жит решение задачи, описанное в § 17, где

по фронтальной проекции Аг точки А, при-

надлежащей данной плоскости, определя-

лась ее горизонтальная проекция А\.

} 38. ПРОЕКЦИИ плоских

АЛГЕБРАИЧЕСКИХ ЛИНИЯ

Плоской алгебраической кривой

называется кривая, определяемая в де-

картовых координатах уравнением

/(*,</) = 0, (7.4)

где f(x, у) — многочлен от х и у. Если

f(x,y) представляет собой многочлен п-й

степени, то линия, определяемая уравне-

нием (7.4), называется алгебраиче-

ской линией n-го порядка.

Число действительных точек пересече-

ния алгебраической кривой т с произволь-

ной прямой линией не может быть больше

порядка кривой.

Известны линии, число точек пересече-

ния которых с любой прямой всегда мень-

ше порядка этой кривой. Например, линия,

определяемая уравнением у = х* (рис.

176), пересекается с любой прямой не

более чем в двух действительных точках.

Порядок плоской алгебраической кри-

Рис. 176

вой сохраняется при ее ортогональном

проецировании.

В качестве примера рассмотрим ортого-

нальную проекцию гп\ кривой второго по-

рядка — окружности, плоскость которой

а составляет с плоскостью 111 угол <р (рис.

177).

Один из диаметров окружности — тот,

что параллелен плоскости П>, спроециру-

ется в натуральную величину. Этим диа-

метром является отрезок АВ. Его проек-

ция AiBi=AB.

Все хорды, перпендикулярные диаметру

АВ, сокращаются в cos ср раз. Так MiN\ =

MN cos <р. Нетрудно показать, что про-

екция окружности есть эллипс с большей

осью 2a = j4iBi и коэффициентом сжатия

cosq>.

В самом деле, в системе хОу

(Од;||

Пi)

окружность m определяется уравнением

+ у

= а

, (7.5)

а так как

(О

\\Ох)

у = у

:cos

<р,

(7.6)

то подстановка (7.6) в (7.5) дает

cos <р

или

где

— a cos <р.

Итак, ортогональная проекция окруж-

ности радиуса а есть эллипс с полуосями

а и a cos ф.

Аналогично можно доказать, что орто-

гональной проекцией эллипса является эл-

липс, гиперболы — гипербола и парабо-

лы — парабола.

Иными словами, аффинный класс кри-

вой второго порядка сохраняется при ор-

тогональном проецировании. Здесь исклю-

чены случаи вырождения проекций в пря-

мые линии, когда плоскость кривой

перпендикулярна плоскости проекций.

Выясним теперь вопрос о числе точек,

определяющих кривую второго порядка,

которая в любой декартовой системе ко-

ординат задается уравнением

+ 2апху + а

у'

+ 2а

х + 2а

у + а

= 0. (7.8)

Если кривая второго порядка задана

достаточным числом точек, принадлежа-

щих ей, то для определения уравнения

этой линии следует по данным условиям

(координатам точек) вычислить коэффи-

циенты уравнения (7.8). Так как в рас-

сматриваемом уравнении хотя бы один из

коэффициентов ац, а\

и а

отличен от

нуля, то, разделив на него обе части урав-

нения (7.8), получим равносильное ему

уравнение с пятью неизвестными коэффи-

циентами. Для вычисления коэффициен-

тов необходимо знать пять точек, коорди-

наты которых должны удовлетворять

уравнению. (7.8). В аналитической геомет-

рии [1] доказывается, что если из пяти

данных точек никакие четыре не лежат на

одной прямой, то через пять данных точек

проходит единственная линия второго по-

рядка.

Как определить любую другую точку

кривой второго порядка по пяти задан-

ным?

На этот вопрос дает ответ теорема Пас-

каля, утверждающая, что во всяком шес-

тиугольнике, вписанном в кривую второго

порядка (эллипс, гиперболу, параболу),

точки пересечения трех пар противопо-

ложных сторон лежат на одной прямой,

называемой прямой Паскаля; при этом

шестиугольник может быть как выпуклым,

так и звездчатым. Противоположными

сторонами считают такие, которые отделе-

ны двумя сторонами. В шестиугольнике,

изображенном на рис. 178, противополож-

ными сторонами являются стороны АВ и

DE, ВС и EF, CD и FA.

Опуская доказательство этой теоремы,

с которым можно ознакомиться в специ-

альной литературе по проективной геомет-

рии [21], покажем, как по пяти данным

точкам А, В, С, D, Е можно построить

сколько угодно других точек той же кри-

вой.

Принимая эти пять точек за вершины

шестиугольника, вписанного в кривую вто-

рого порядка, построим четыре его сторо-

ны АВ, ВС, CD, DE и зададимся направ-

лением EN пятой.

Для построения прямой Паскаля вос-

пользуемся двумя точками K==AB(]DE и

L — BC0.EN. Третья пара противополож-

ных сторон шестиугольника должна пе-

ресечь прямую Паскаля в точке M = CDf)

KL. Через эту точку М и пройдет шестая

сторона вписанного шестиугольника. Вер-

шина F будет определена пересечением

прямых EN и AM.

Аналогично, меняя направление прямой

EN, можно построить сколько угодно точек

кривой второго порядка, проходящей через

пять заданных точек.

Заметим, что теорема Паскаля примени-

ма и к многоугольникам, число вершин

которых меньше шести. В этих случаях

следует только предположить, что какие-

либо вершины совпадают, а стороны, сое-

диняющие эти совпавшие вершины, явля-

ются уже не хордами, а касательными

к кривой.

Так, кривая второго порядка вполне оп-

ределяется тремя точками А, В и С и ка-

сательными АР и ВТ в двух из них (рис.

179).

Чтобы применить теорему к вписанному

Рис. 178

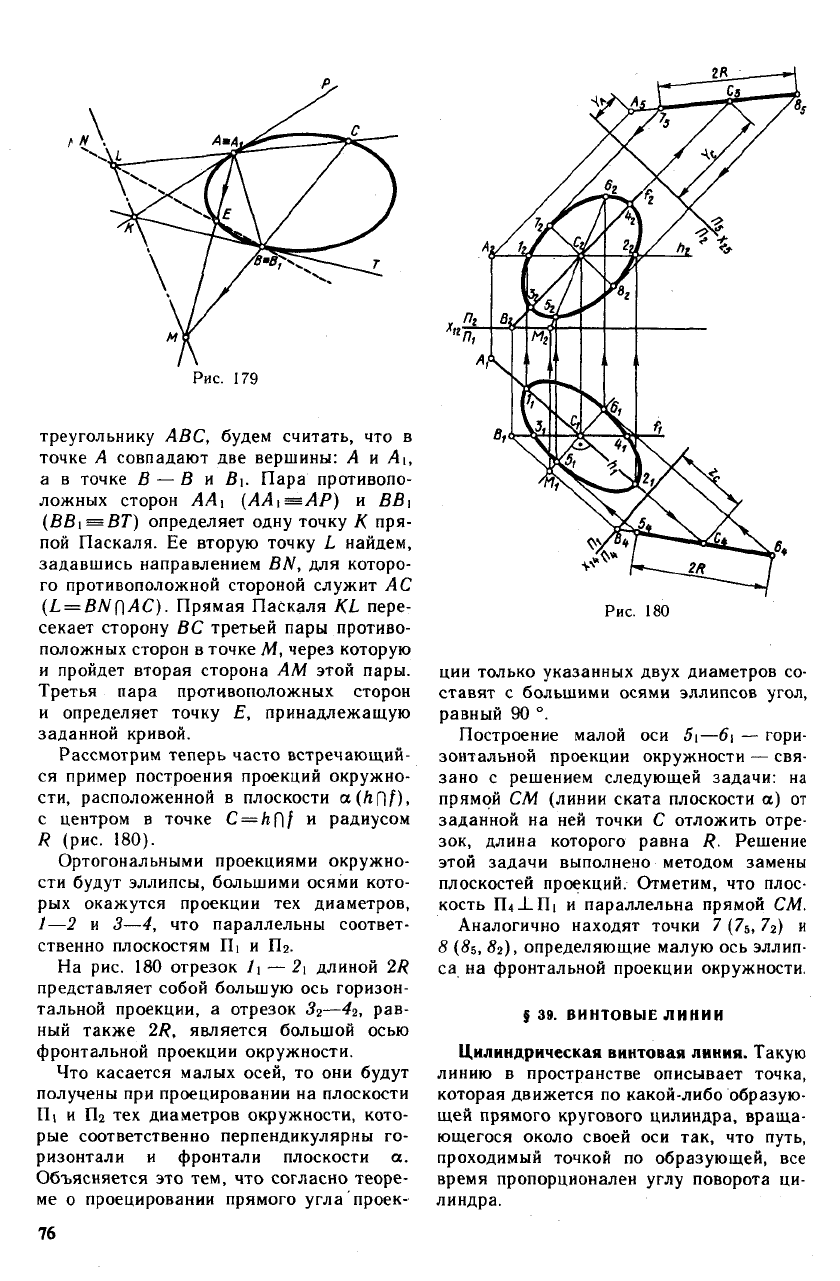
треугольнику ABC, будем считать, что в

точке А совпадают две вершины: А и А\,

а в точке В — В и В\. Пара противопо-

ложных сторон АА1 (АА\=АР) и ВВ\

(BBi^BT) определяет одну точку К при-

пой Паскаля. Ее вторую точку L найдем,

задавшись направлением BN, для которо-

го противоположной стороной служит АС

(L = BN(]AC). Прямая Паскаля KL пере-

секает сторону ВС третьей пары противо-

положных сторон в точке М, через которую

и пройдет вторая сторона AM этой пары.

Третья пара противоположных сторон

и определяет точку Е, принадлежащую

заданной кривой.

Рассмотрим теперь часто встречающий-

ся пример построения проекций окружно-

сти, расположенной в плоскости a(Af|/),

с центром в точке С

== /г П

/ и радиусом

R (рис. 180).

Ортогональными проекциями окружно-

сти будут эллипсы, большими осями кото-

рых окажутся проекции тех диаметров,

/—2 и 3—4, что параллельны соответ-

ственно плоскостям Hi и Пг-

На рис. 180 отрезок

—

длиной 2R

представляет собой большую ось горизон-

тальной проекции, а отрезок 3

—4

, рав-

ный также 2R, является большой осью

фронтальной проекции окружности.

Что касается малых осей, то они будут

получены при проецировании на плоскости

Hi и Пг тех диаметров окружности, кото-

рые соответственно перпендикулярны го-

ризонтали и фронтали плоскости а.

Объясняется это тем, что согласно теоре-

ме о проецировании прямого угла проек-

ции только указанных двух диаметров со-

ставят с большими осями эллипсов угол,

равный 90

Построение малой оси 51—61 — гори-

зонтальной проекции окружности — свя-

зано с решением следующей задачи: на

прямой СМ (линии ската плоскости а) от

заданной на ней точки С отложить отре-

зок, длина которого равна R. Решение

этой задачи выполнено методом замены

плоскостей проекций. Отметим, что плос-

кость Ш-1-П1 и параллельна прямой СМ.

Аналогично находят точки 7 (7s, 7

) и

8 (#5, 8

), определяющие малую ось эллип-

са на фронтальной проекции окружности.

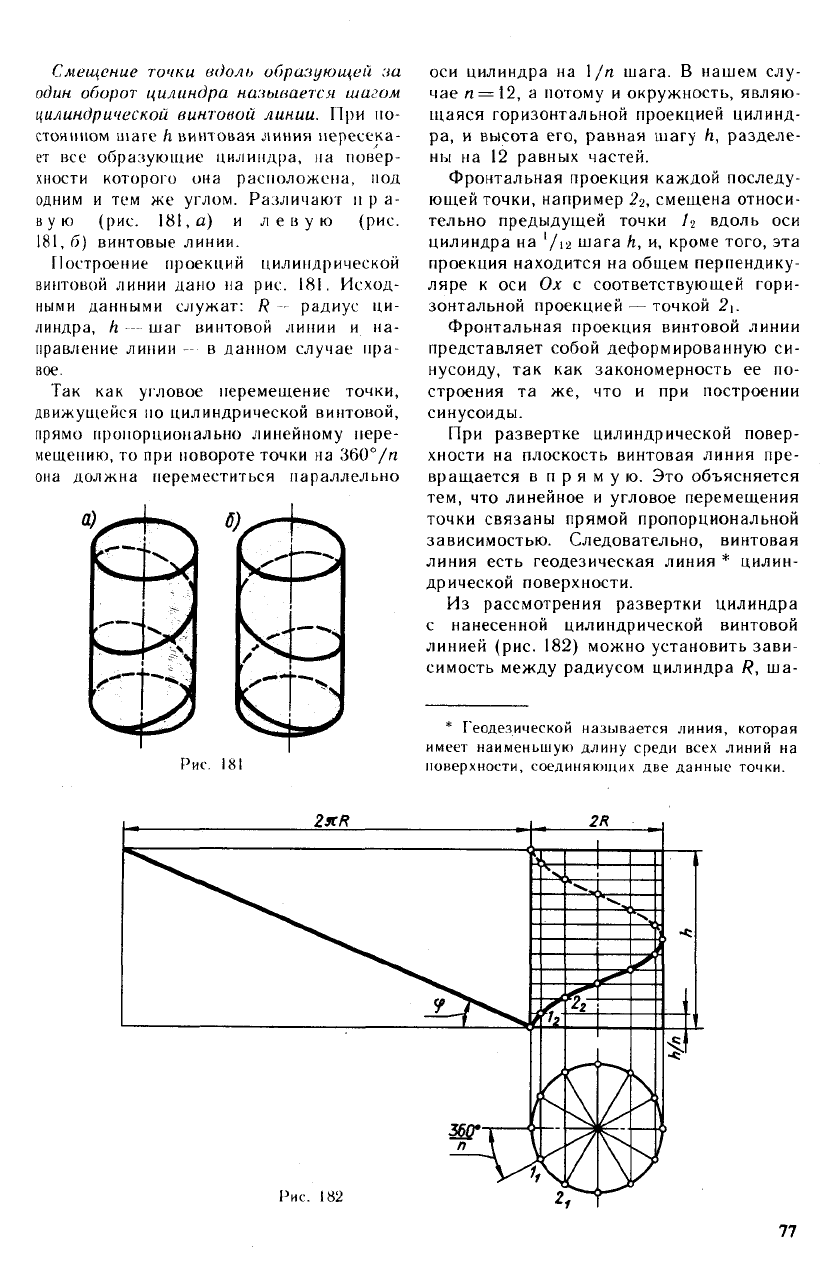
§ 39. ВИНТОВЫЕ ЛИНИИ

Цилиндрическая винтовая линия. Такую

линию в пространстве описывает точка,

которая движется по какой-либо образую-

щей прямого кругового цилиндра, враща-

ющегося около своей оси так, что путь,

проходимый точкой по образующей, все

время пропорционален углу поворота ци-

линдра.

оси цилиндра на

/п шага. В нашем слу-

чае п = 12, а потому и окружность, являю-

щаяся горизонтальной проекцией цилинд-

ра, и высота его, равная шагу h, разделе-

ны на 12 равных частей.

Фронтальная проекция каждой последу-

ющей точки, например смещена относи-

тельно предыдущей точки /

вдоль оси

цилиндра на '/12 шага h, и, кроме того, эта

проекция находится на общем перпендику-

ляре к оси Ох с соответствующей гори-

зонтальной проекцией — точкой 2\.

Фронтальная проекция винтовой линии

представляет собой деформированную си-

нусоиду, так как закономерность ее по-

строения та же, что и при построении

синусоиды.

При развертке цилиндрической повер-

хности на плоскость винтовая линия пре-

вращается в прямую. Это объясняется

тем, что линейное и угловое перемещения

точки связаны прямой пропорциональной

зависимостью. Следовательно, винтовая

линия есть геодезическая линия * цилин-

дрической поверхности.

Из рассмотрения развертки цилиндра

с нанесенной цилиндрической винтовой

линией (рис. 182) можно установить зави-

симость между радиусом цилиндра R, ша-

* Геодезической называется линия, которая

имеет наименьшую длину среди всех линий на

поверхности, соединяющих две данные точки.

Смещение точки вдоль образующей за

один оборот цилиндра называется шагом

цилиндрической винтовой линии. При по-

стоянном mare h винтовая линия пересека-

ет все образующие цилиндра, на повер-

хности которого она расположена, под

одним и тем же углом. Различают м р а-

вую (рис. 181, а) и левую (рис.

181,6) винтовые линии.

Построение проекций цилиндрической

винтовой линии дано на рис. 181. Исход-

ными данными служат: R — радиус ци-

линдра, h -— шаг винтовой линии и на-

правление линии - в данном случае пра-

вое.

Так как угловое перемещение точки,

движущейся по цилиндрической винтовой,

прямо пропорционально линейному пере-

мещению, то при повороте точки на 360°/я

она должна переместиться параллельно

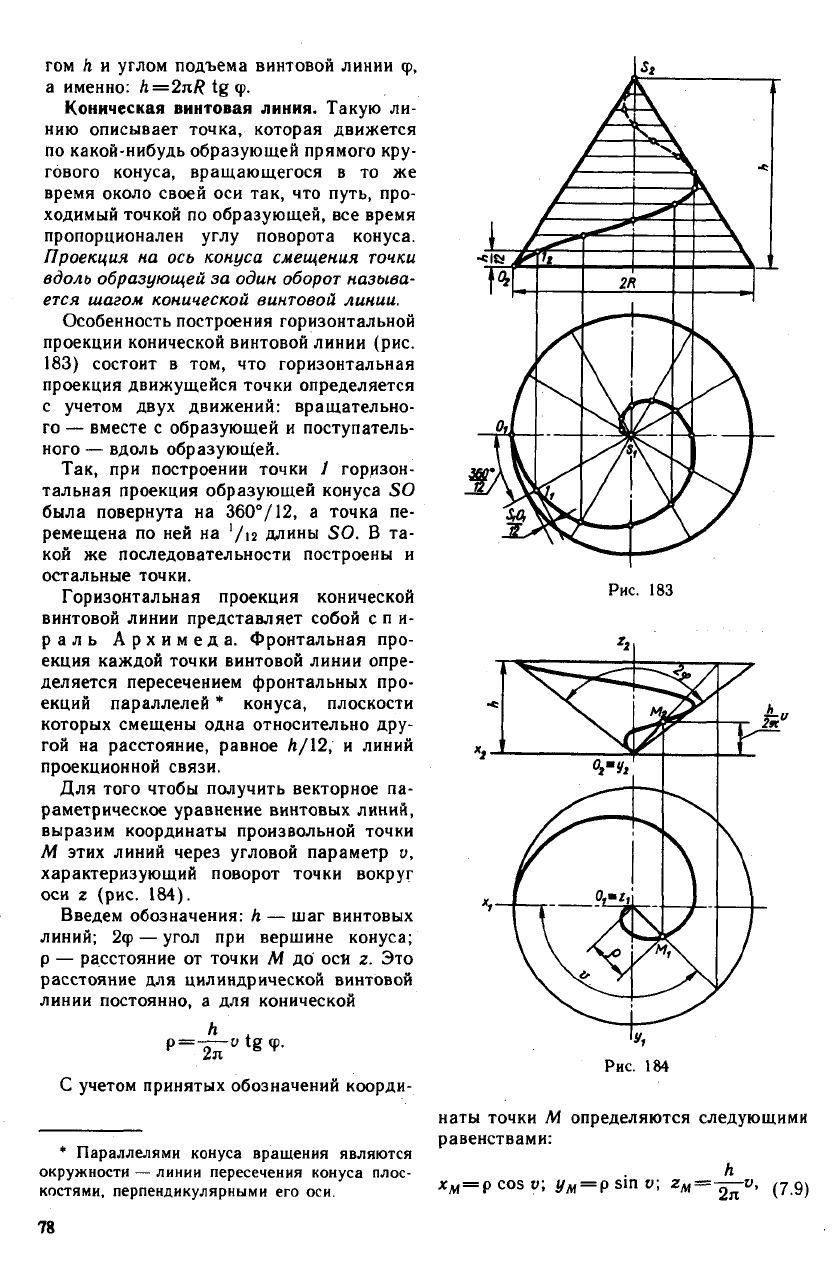
гом h и углом подъема винтовой линии ср,

а именно:

= 2n/?tg<p.

Коническая винтовая линия. Такую ли-

нию описывает точка, которая движется

по какой-нибудь образующей прямого кру-

гового конуса, вращающегося в то же

время около своей оси так, что путь, про-

ходимый точкой по образующей, все время

пропорционален углу поворота конуса.

Проекция на ось конуса смещения точки

вдоль образующей за один оборот называ-

ется шагом конической винтовой линии.

Особенность построения горизонтальной

проекции конической винтовой линии (рис.

183) состоит в том, что горизонтальная

проекция движущейся точки определяется

с учетом двух движений: вращательно-

го — вместе с образующей и поступатель-

ного — вдоль образующей.

Так, при построении точки / горизон-

тальная проекция образующей конуса SO

была повернута на 360°/12, а точка пе-

ремещена по ней на '/12 длины SO. В та-

кой же последовательности построены и

остальные точки.

Горизонтальная проекция конической

винтовой линии представляет собой спи-

раль Архимеда. Фронтальная про-

екция каждой точки винтовой линии опре-

деляется пересечением фронтальных про-

екций параллелей * конуса, плоскости

которых смещены одна относительно дру-

гой на расстояние, равное Л/12, и линий

проекционной связи.

Для того чтобы получить векторное па-

раметрическое уравнение винтовых линий,

выразим координаты произвольной точки

М этих линий через угловой параметр v,

характеризующий поворот точки вокруг

оси z (рис. 184).

Введем обозначения: h — шаг винтовых

линий;

2qp

— угол при вершине конуса;

р — расстояние от точки М до оси г. Это

расстояние для цилиндрической винтовой

линии постоянно, а для конической

С учетом принятых обозначений коорди-

Рис. 183

* Параллелями конуса вращения являются

окружности — линии пересечения конуса плос-

костями, перпендикулярными его оси.

Рис. 184

наты точки М определяются следующими

равенствами:

=pcos v; у

= psinn; (7.9)

а уравнение цилиндрнческон и коническом

винтовой линии можно записать в виде

OM — p(i cos v + / sin и) +——v-k.

(7.10)

Вопросы и задачи для самоконтроля

1. Построить проекции окружности, задан-

ной диаметром АВ и фронтальной проекцией Сг

одной из принадлежащих ей точек (рис. 185).

2. Построить проекции окружности, которая

задана центром С и касательной I.

3. Кривую /, расположенную в плоскости Пь

повернуть вокруг оси i на 60° (рис. 186).

4. Точка М движется по правой винтовой

линии с шагом р — 120 мм. Построить ее про-

екции, соответствующие угловому перемеще-

нию, равному 120". Первоначальное положение

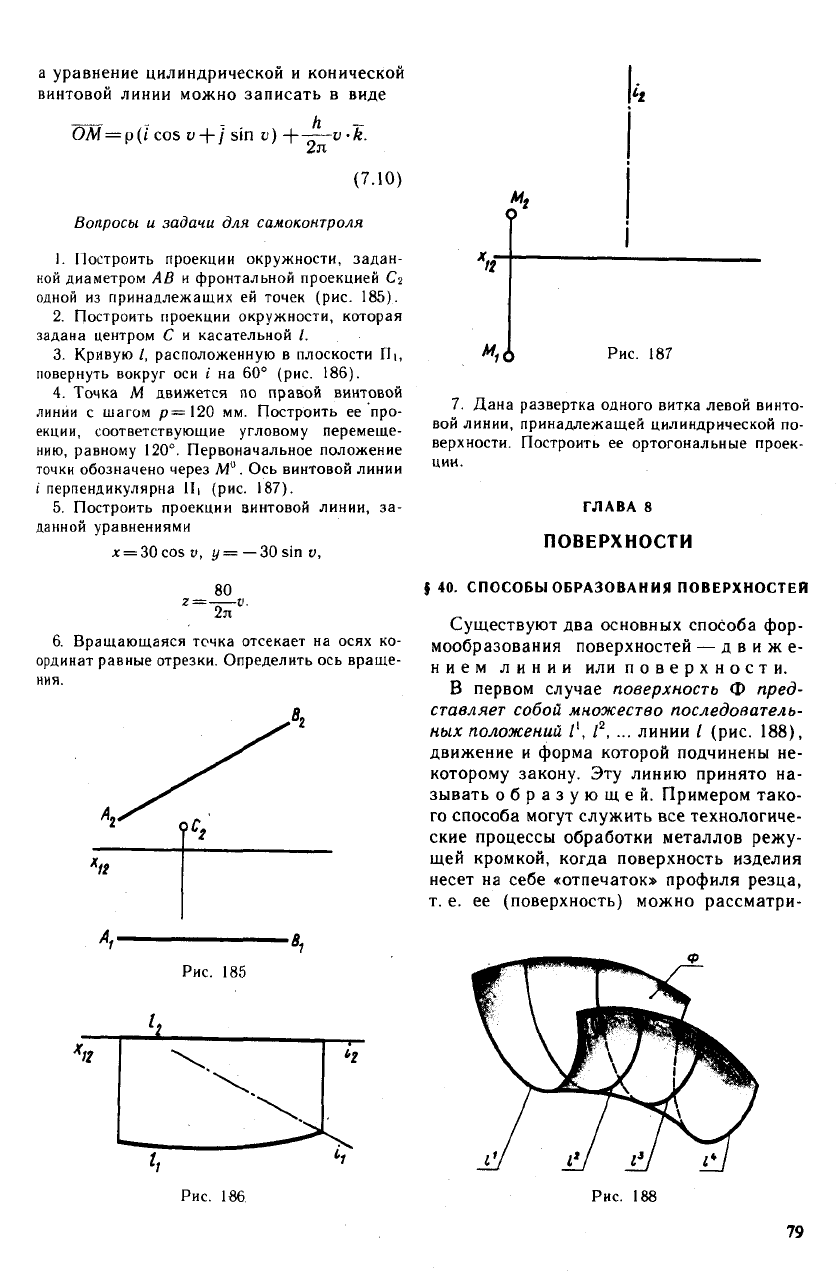
точки обозначено через М

. Ось винтовой линии

i перпендикулярна IIi (рис. 187).

5. Построить проекции винтовой линии, за-

данной уравнениями

= 30cost>, у=—30 sin у,

_80

2л

-о.

6. Вращающаяся точка отсекает на осях ко-

ординат равные отрезки. Определить ось враще-

ния.

Рис. 185

М.

/О

Рис. 187

7. Дана развертка одного витка левой винто-

вой линии, принадлежащей цилиндрической по-

верхности. Построить ее ортогональные проек-

ции.

ГЛАВА 8

ПОВЕРХНОСТИ

$ 40. СПОСОБЫ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ

Существуют два основных способа фор-

мообразования поверхностей — движе-

нием линии или поверхности.

В первом случае поверхность Ф пред-

ставляет собой множество последователь-

ных положений /', /

, ... линии I (рис. 188),

движение и форма которой подчинены не-

которому закону. Эту линию принято на-

зывать образующей. Примером тако-

го способа могут служить все технологиче-

ские процессы обработки металлов режу-

щей кромкой, когда поверхность изделия

несет на себе «отпечаток» профиля резца,

т. е. ее (поверхность) можно рассматри-

Рис. 186. Рис. 188