Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

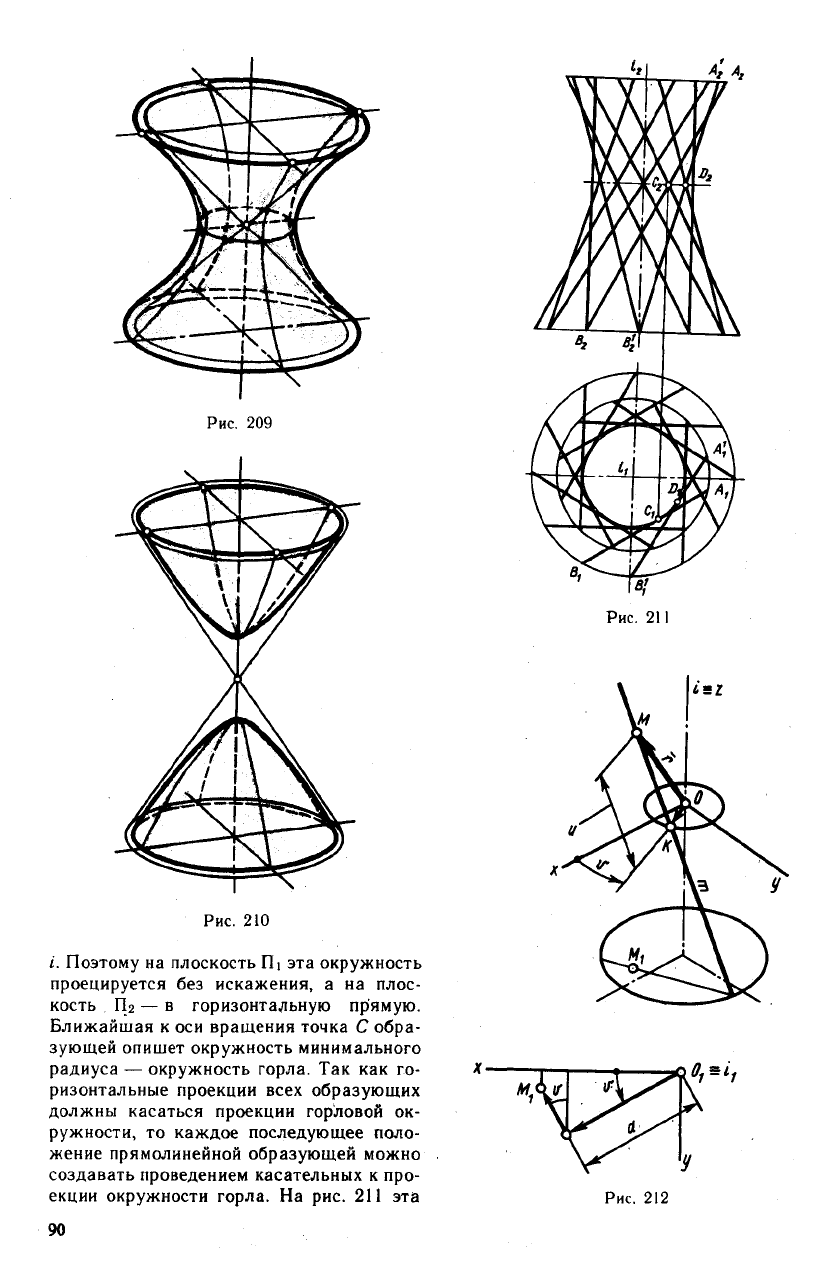
Рис. 210

i. Поэтому на плоскость Ш эта окружность

проецируется без искажения, а на плос-

кость П

— в горизонтальную прямую.

Ближайшая к оси вращения точка С обра-

зующей опишет окружность минимального

радиуса — окружность горла. Так как го-

ризонтальные проекции всех образующих

должны касаться проекции горловой ок-

ружности, то каждое последующее поло-

жение прямолинейной образующей можно

создавать проведением касательных к про-

екции окружности горла. На рис. 211 эта

окружность разделена на двенадцать рав-

ных частей. К проекции ее в точке D\

проведена касательная А\В\ — горизон-

тальная проекция образующей, поверну-

той на 30°. Ее фронтальная проекция оп-

ределена точками Ai и В\, каждая из

которых расположена в плоскости своей

параллели. Аналогично проводят построе-

ние и остальных образующих.

Радиус-вектор г произвольной точки

М поверхности однополостного гиперболо-

ида вращения (рис. 212) можно предста-

вить в виде

? = т +

~КМ,

(8.23)

а его координаты

х = а cos v-\-u cos

ср

sin vЛ

у = a sin v — и cos

ср

cos v, I (8.24)

z=usin<p, j

где ф — угол наклона образующей т к

плоскости хОу; v, и — соответственно уг-

ловой и линейный параметры поверхности

(v — определяет угол поворота образую-

щей вокруг оси (', а линейный параметр

и фиксирует точку на т).

Покажем, что меридианом такой повер-

хности является гипербола. Действитель-

но, сложив возведенные в квадрат левые

и правые части первых двух равенств

(8.24), будем иметь

+у

= а

+ и

cos

ф, (8.25)

а так как u = z/sin ф, то выражение (8.25)

можно записать так:

-\-у

— z

ctg

= а

. (8.26)

Присоединив к (8.26) уравнение плоско-

сти у = 0, убеждаемся в том, что меридиа-

ном поверхности является гипербола, оп-

ределяемая уравнением

4~4 ctg

«p=l. (8.27)

а а

Идея применения однополостного гипер-

болоида вращения в строительной технике

принадлежит выдающемуся русскому ин-

женеру, почетному члену Академии наук

СССР Владимиру Григорьевичу Шухову

(1853—1939). Им была предложена кон-

струкция башни, состоящей из прямоли-

нейных элементов. Технологичность кон-

струкции в сочетании с ажурной изящной

формой обеспечила в свое время широкое

распространение башни в качестве радио-

мачт, маяков, водонапорных башен, опор

для линий электропередач.

По проекту и под руководством

В. Г. Шухова в 1921 г. в Москве была

построена радиомачта на Шаболовке вы-

сотой 160 м из шести секций — шести

гиперболоидов.

Не ослаб интерес к этой поверхности

и в наши дни. На рис. 213 эскизно показан

один из проектов покрытия планетария

(США), линейчатый каркас которого об-

разует поверхность однополостного гипер-

болоида.

$ 43. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ

Развертывающейся называется такая

линейчатая поверхность, которую можно

без складок и разрывов развернуть на

плоскость. Линейчатость поверхности —

необходимый, но не достаточный признак

развертываемости.

В дифференциальной геометрии доказы-

вается, что к развертывающимся повер-

хностям относятся цилиндрическая, кони-

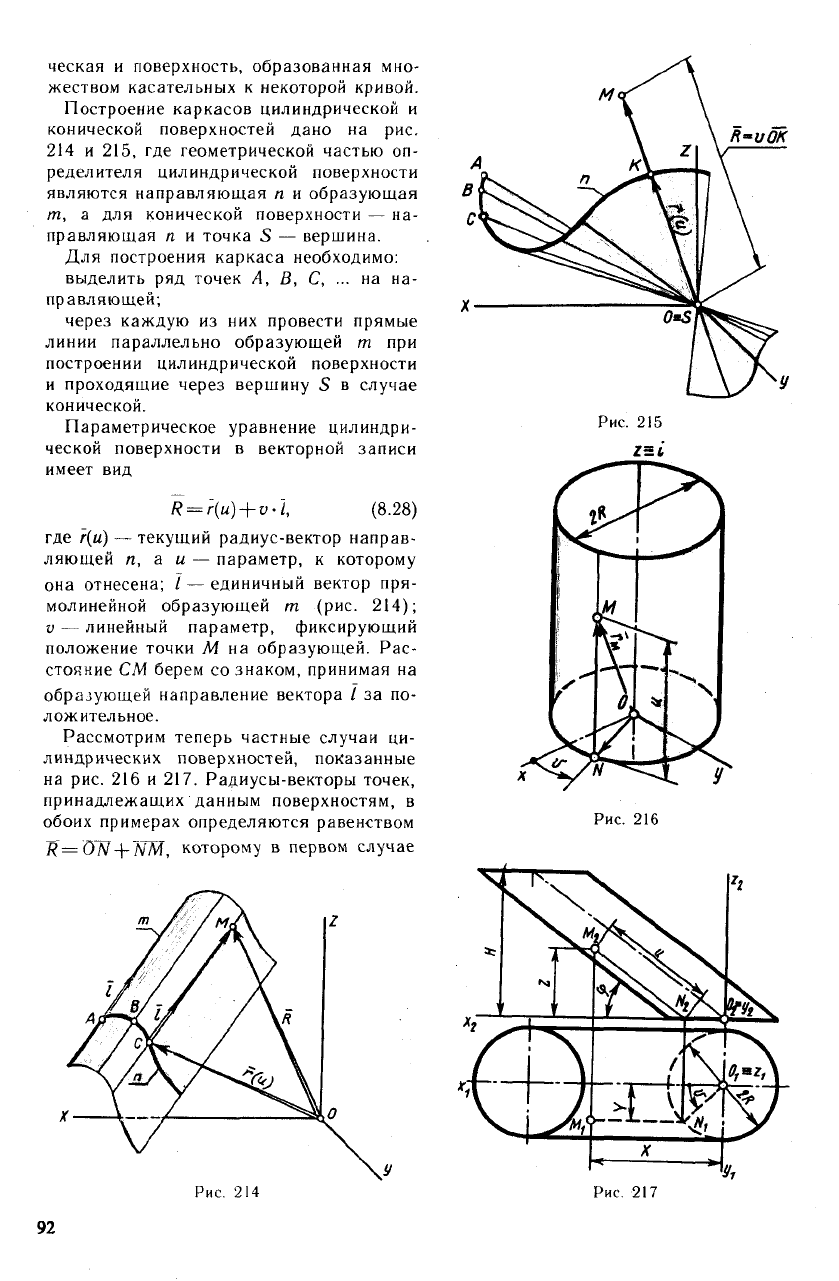
ческая и поверхность, образованная мно-

жеством касательных к некоторой кривой.

Построение каркасов цилиндрической и

конической поверхностей дано на рис.

214 и 215, где геометрической частью оп-

ределителя цилиндрической поверхности

являются направляющая я и образующая

т, а для конической поверхности — на-

правляющая п и точка S — вершина.

Для построения каркаса необходимо:

выделить ряд точек А, В, С, ... на на-

правляющей;

через каждую из них провести прямые

линии параллельно образующей т при

построении цилиндрической поверхности

и проходящие через вершину S в случае

конической.

Параметрическое уравнение цилиндри-

ческой поверхности в векторной записи

имеет вид

R = r(u) + vi, (8.28)

где г(и) — текущий радиус-вектор направ-

ляющей п, а и — параметр, к которому

она отнесена; / — единичный вектор пря-

молинейной образующей т (рис. 214);

v — линейный параметр, фиксирующий

положение точки М на образующей. Рас-

стояние СМ берем со знаком, принимая на

образующей направление вектора / за по-

ложительное.

Рассмотрим теперь частные случаи ци-

линдрических поверхностей, показанные

на рис. 216 и 217. Радиусы-векторы точек,

принадлежащих данным поверхностям, в

обоих примерах определяются равенством

R = UN

-\-~NM,

которому в первом случае

Z=i

Рис. 216

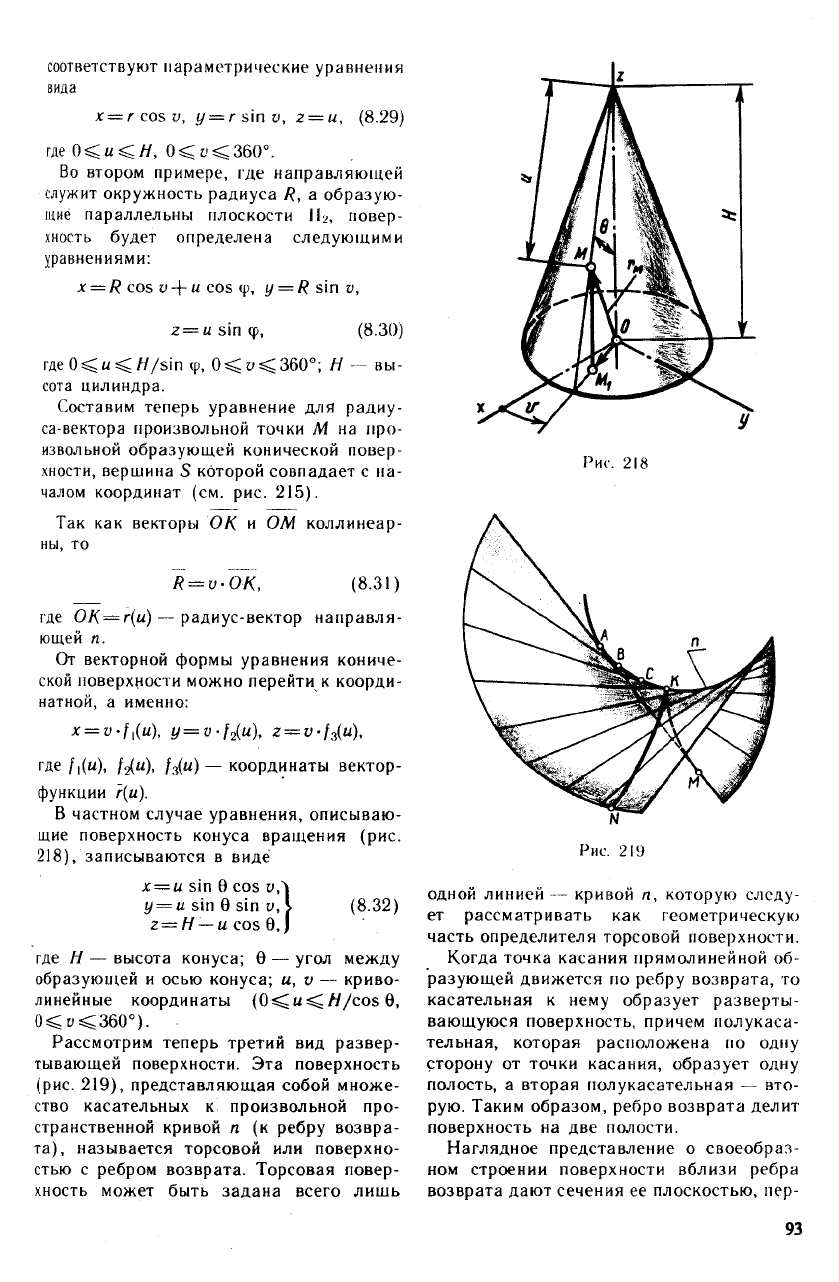
соответствуют параметрические уравнения

вида

* = rcosu, у —г sin у, г —и, (8.29)

гдеО<ы<//, 0<t'<360°.

Во втором примере, где направляющей

служит окружность радиуса R, а образую-

щие параллельны плоскости П

, повер-

хность будет определена следующими

уравнениями:

x = R cos v-\-u cos (p, y =

sin v,

г=изтф, (8.30)

где 0<u<///sin ф, 0<o<360°; H — вы-

сота цилиндра.

Составим теперь уравнение для радиу-

са-вектора произвольной точки М на про-

извольной образующей конической повер-

хности, вершина S которой совпадает с на-

чалом координат (см. рис. 215).

Так как векторы ОК и ОМ коллинеар-

ны, то

R — v-OK, (8.31)

где ОК=г(и) — радиус-вектор направля-

ющей п.

От векторной формы уравнения кониче-

ской поверхности можно перейти к коорди-

натной, а именно:

x = vf

(u), y = vf^u), z = v-f

(u),

где fi(u), fjjj), /з(") — координаты вектор-

функции г(и).

В частном случае уравнения, описываю-

щие поверхность конуса вращения (рис.

218), записываются в виде

х=и sin 9 cos кЛ

у = и sin 0 sin v, I (8.32)

z—H

— u

cos 0, j

где H — высота конуса; 0 — угол между

образующей и осью конуса; и, v — криво-

линейные координаты (0<Г и ^ ///cos 0,

0<w<360°).

Рассмотрим теперь третий вид развер-

тывающей поверхности. Эта поверхность

(рис. 219), представляющая собой множе-

ство касательных к произвольной про-

странственной кривой л (к ребру возвра-

та), называется торсовой или поверхно-

стью с ребром возврата. Торсовая повер-

хность может быть задана всего лишь

Рис. 219

одной линией — кривой п, которую следу-

ет рассматривать как геометрическую

часть определителя торсовой поверхности.

Когда точка касания прямолинейной об-

разующей движется по ребру возврата, то

касательная к нему образует разверты-

вающуюся поверхность, причем полукаса-

тельная, которая расположена по одну

сторону от точки касания, образует одну

полость, а вторая полукасательная — вто-

рую. Таким образом, ребро возврата делит

поверхность на две полости.

Наглядное представление о своеобраз-

ном строении поверхности вблизи ребра

возврата дают сечения ее плоскостью, пер-

пендикулярной образующей и проходящей

через точку касания данной образующей.

На рис. 219 показано одно из таких сече-

ний — кривая вида MKN, которая имеет

в К точку возврата. В этой точке встреча-

ются ветви кривой МК и NK- Точки ребра

возврата являются особыми точками.

Развертывающиеся поверхности обла-

дают ценным технологическим свойством:

их можно обработать плоским инструмен-

том, движение которого определяется

только одним параметром.

В процессе обработки плоскость режу-

щего инструмента, перемещаясь относи-

тельно заготовки, образует семейство

плоскостей от одного параметра. Этим па-

раметром может быть время, угловое пе-

ремещение инструмента и т. п. Обрабаты-

ваемая поверхность, таким образом, явля-

ется огибающей однопараметрического

семейства плоскостей, что, как это доказы-

вается в дифференциальной геометрии,

необходимо и достаточно для того, чтобы

поверхность была развертывающейся.

Укажем на один важный случай развер-

тывающейся поверхности, когда ребром

возврата поверхности служит цилин-

дрическая винтовая линия. Эта

поверхность интересна не только своими

особыми геометрическими свойствами, но

и применением, которое она имеет в тех-

нике.

Итак, пусть ребром возврата является

цилиндрическая винтовая линия п, изо-

браженная на рис. 220. На том же чертеже

показаны и касательные к винтовой. От-

резки касательных обозначены через 1 —

— М\ 2-М\ 3 — М\ ...

Если поверхность, ребром возврата ко-

торой служит цилиндрическая винтовая,

пересечь плоскостью, перпендикулярной

оси цилиндра, то в сечении получим

эвольвенту, эволютой * которой явля-

ете^ окружность — ортогональная проек-

ция ребра возврата на ту же плоскость.

Справедливость этого утверждения вы-

текает из закона образования поверхно-

сти: когда прямая линия движется в про-

* Эволютой кривой линии называется

множество центров ее кривизны. Кривая линия

по отношению к ее эволюте называется эволь-

вентой. Нормали эвольвенты будут касатель-

ными к эволюте.

странстве, оставаясь касательной к ци-

линдрической винтовой, проекция каса-

тельной на плоскость, перпендикулярную

оси цилиндра, без скольжения обкатывает

окружность — проекцию ребра возврата

на ту же плоскость. А при таком движении

прямой по окружности каждая точка пря-

мой описывает эвольвенту.

Часто поэтому в технической литературе

данную поверхность называют винтовой

эвольвентной поверхностью. На

рис. 220 эвольвентой окружности радиуса

RO является множество горизонтальных

следов М\, М?, М

\ касательных к ци-

линдрической винтовой п.

Сечение рассматриваемой поверхности

плоскостью а, перпендикулярной оси ци-

линдра, представляет собой также эволь-

венту, каждая точка которой, например К,

определена как точка пересечения соот-

ветствующей касательной с плоскостью

а(аг), т.е. К=(7 — М

)[)а. '

Винтовой эвольвентной поверхностью

являются откосы насыпи и выемки полот-

на железной дороги на кривой с подъемом.

В качестве других примеров применения

этой поверхности в технике можно указать

на поверхности косых зубьев цилиндриче-

ских шестерен, на рабочие поверхности

эвольвентных червяков, используемых в

червячных редукторах, на поверхность ре-

жущих кромок червячных фрез — для на-

резания зубьев шестерен и червячных ко-

лес.

§ 44. ВИНТОВЫЕ ПОВЕРХНОСТИ

Винтовая поверхность образуется вин-

товым

движением некоторой линии. Ли-

ния, совершающая винтовое движение,

называется образующей поверхно-

ст и.

Под винтовым движением понимают

движение, представляющее собой сово-

купность двух движений: поступательного

движения, параллельного некоторой оси

(оси винта), и вращательного вокруг той

же оси. При этом поступательное и угло-

вое перемещения линии находятся в опре-

деленной зависимости: Ah — k-Av, где

ДА— линейное перемещение образующей

за время At\ Av — угловое перемещение ее

за то же время и k — коэффициент про-

порциональности.

Если коэффициент k — величина посто-

янная, то получается поверхность с посто-

янным шагом *; при k переменном — шаг

поверхности также переменный.

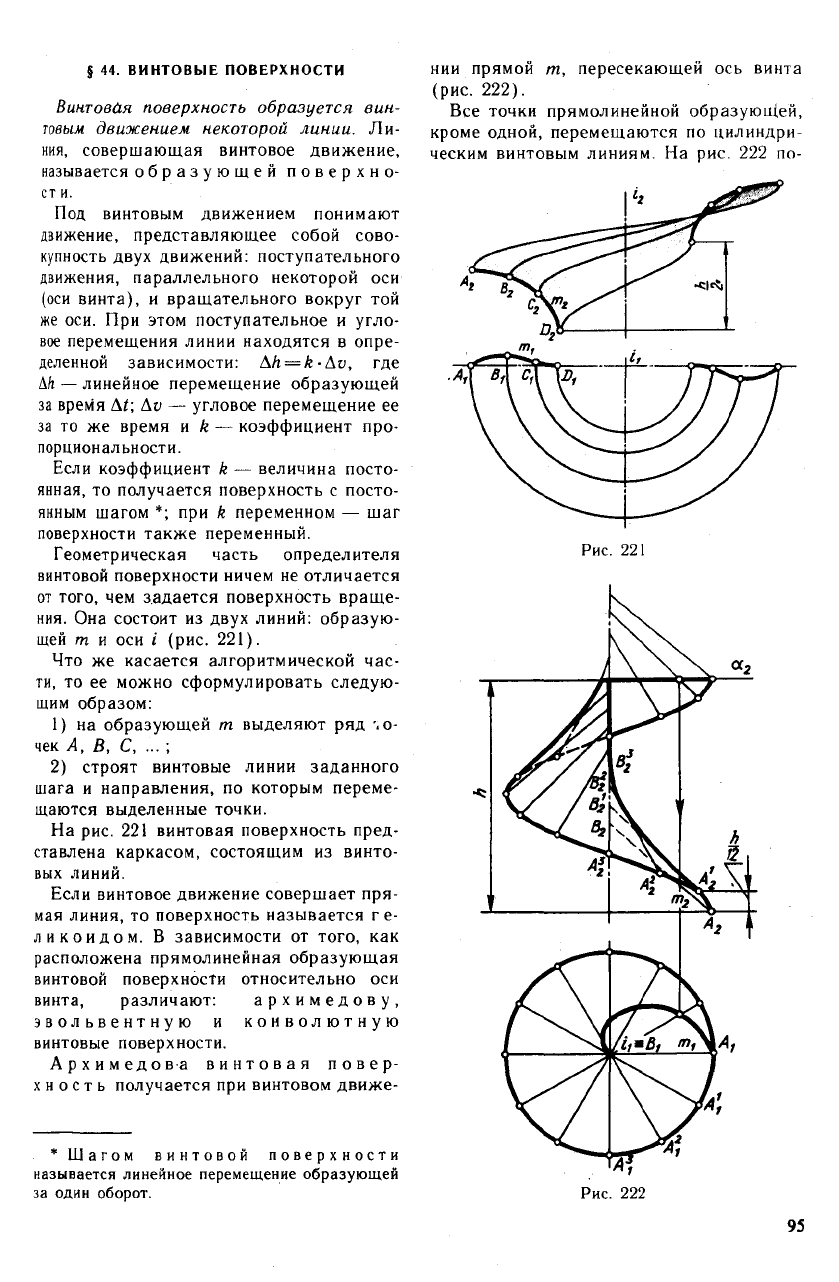
Геометрическая часть определителя

винтовой поверхности ничем не отличается

от того, чем задается поверхность враще-

ния. Она состоит из двух линий: образую-

щей m и оси i (рис. 221).

Что же касается алгоритмической час-

ти, то ее можно сформулировать следую-

щим образом:

1) на образующей m выделяют ряд

.о-

чек А, В, С, ... ;

2) строят винтовые линии заданного

шага и направления, по которым переме-

щаются выделенные точки.

На рис. 221 винтовая поверхность пред-

ставлена каркасом, состоящим из винто-

вых линий.

Если винтовое движение совершает пря-

мая линия, то поверхность называется ге-

ликоидом. В зависимости от того, как

расположена прямолинейная образующая

винтовой поверхности относительно оси

винта, различают: архимедову,

эвольвентную и конволютную

винтовые поверхности.

Архимедова винтовая повер-

хность получается при винтовом движе-

нии прямой т, пересекающей ось винта

(рис. 222).

Все точки прямолинейной образующей,

кроме одной, перемещаются по цилиндри-

ческим винтовым линиям. На рис. 222 по-

Рис. 221

* Шагом винтовой поверхности

называется линейное перемещение образующей

за один оборот.

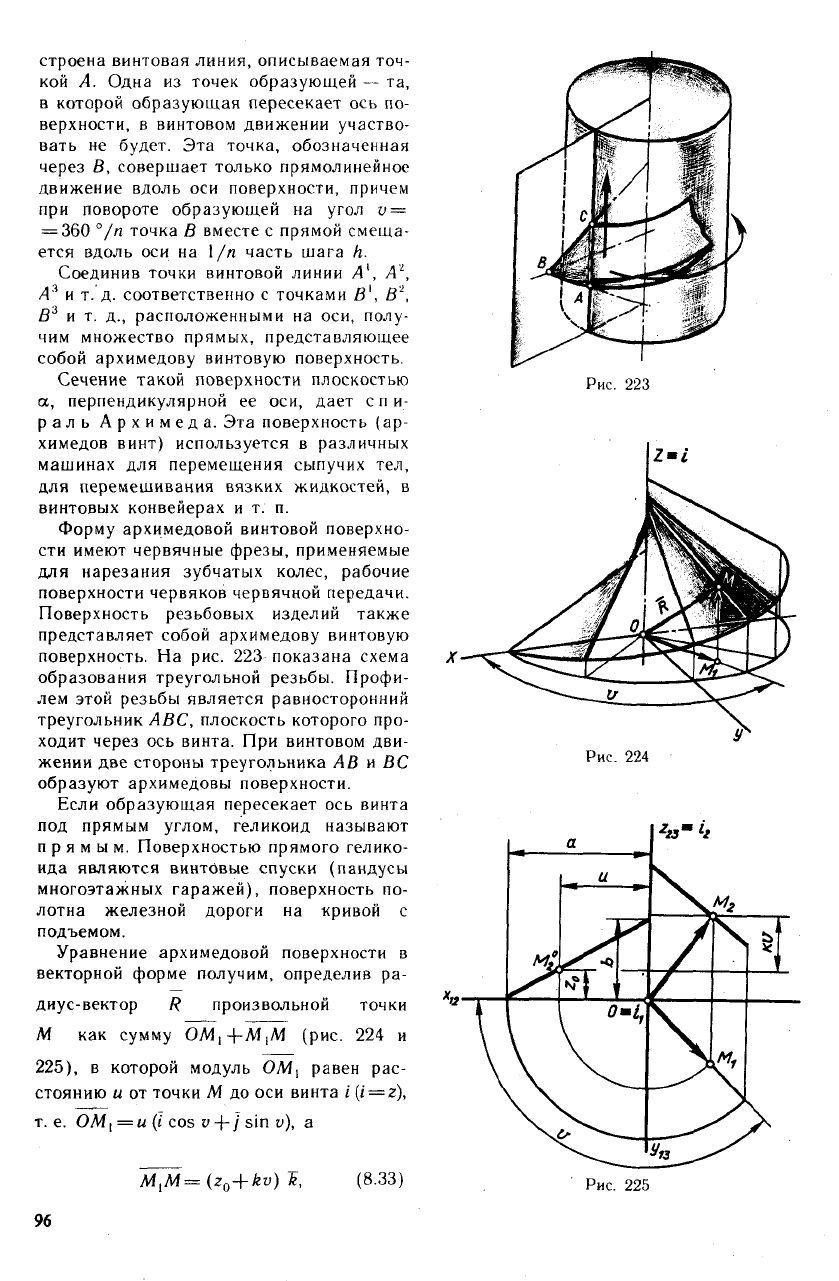
строена винтовая линия, описываемая точ-

кой А. Одна из точек образующей — та,

в которой образующая пересекает ось по-

верхности, в винтовом движении участво-

вать не будет. Эта точка, обозначенная

через В, совершает только прямолинейное

движение вдоль оси поверхности, причем

при повороте образующей на угол

= 360 °/п точка В вместе с прямой смеща-

ется вдоль оси на

/п часть шага h.

Соединив точки винтовой линии А

, А'

и т. д. соответственно с точками В

, В

и т. д., расположенными на оси, полу-

чим множество прямых, представляющее

собой архимедову винтовую поверхность.

Сечение такой поверхности плоскостью

а, перпендикулярной ее оси, дает с п и-

раль Архимеда. Эта поверхность (ар-

химедов винт) используется в различных

машинах для перемещения сыпучих тел,

для перемешивания вязких жидкостей, в

винтовых конвейерах и т. п.

Форму архимедовой винтовой поверхно-

сти имеют червячные фрезы, применяемые

для нарезания зубчатых колес, рабочие

поверхности червяков червячной передачи.

Поверхность резьбовых изделий также

представляет собой архимедову винтовую

поверхность. На рис. 223 показана схема

образования треугольной резьбы. Профи-

лем этой резьбы является равносторонний

треугольник ABC, плоскость которого про-

ходит через ось винта. При винтовом дви-

жении две стороны треугольника АВ и ВС

образуют архимедовы поверхности.

Если образующая пересекает ось винта

под прямым углом, геликоид называют

прямым. Поверхностью прямого гелико-

ида являются винтовые спуски (пандусы

многоэтажных гаражей), поверхность по-

лотна железной дороги на кривой с

подъемом.

Уравнение архимедовой поверхности в

векторной форме получим, определив ра-

диус-вектор R произвольной точки

М как сумму ОМ|4-М,М (рис. 224 и

225), в которой модуль ОМ, равен рас-

стоянию и от точки М до оси винта i

= z),

т. е. ОМ

= u(i cos

-f- j sin v), a

M= (z

+ kv) k, (8.33)

где z

=b (

—— I; k— ; h — шаг вин-

Л a J 2л

та; v — угловое перемещение точки М,

которому соответствует смещение точки

вдоль оси винта на величину kv.

Итак, вектор-функция, описывающая

винтовую архимедову поверхность, имеет

вид

R (и, v) =м (i cos v-\-j sin uJH"

+ (z

+ kv)~k. ' (8.34)

Эвольвентная винтовая поверхность,

рассмотренная выше (см. рис. 220) как

развертывающаяся поверхность, пред-

ставляющая собой множество касатель-

ных к цилиндрической винтовой, может

быть образована и иначе: винтовым дви-

жением прямолинейной образующей, не

пересекающей оси винта.

Движение образующей совершается

при следующем условии: угол подъема

цилиндрической винтовой линии, которую

описывает точка образующей, ближайшая

к оси винта, должен быть равен углу на-

клона образующей к плоскости, перпенди-

кулярной оси винта.

Прямолинейная образующая, совершая

винтовое движение, касается некоторого

цилиндра радиуса Ro (см. рис. 220). Этот

радиус должен быть равен кратчайшему

расстоянию между осью и образующей.

Некоторые свойства и применение вин-

товой эвольвентной поверхности были рас-

смотрены в § 43.

§ 45. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ

С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА

Поверхности с плоскостью параллелиз-

ма

представляют собой множество прямых

(образующих), параллельных некоторой

плоскости (плоскости параллелизма) и

пересекающих две данные линии — на-

правляющие.

Если направляющими являются две

кривые линии, то поверхность называется

цилиндроидом. Если одна из направ-

ляющих — прямая линия, а вторая — кри-

вая, то поверхность называется конои-

дом и, наконец, если обе направляю-

щие — прямые линии, то поверхность

называют гиперболическим пара-

болоидом.

Поверхность цилиндроида определяется

4 Начертательная геометрия

плоскостью параллелизма а (рис. 226)

и двумя криволинейными направляющими

п и п\ которые могут быть пространствен-

ными кривыми или плоскими. В последнем

случае плоскости, в которых расположены

направляющие, не должны совпадать друг

с другом. Прямая линия пг, оставаясь

параллельной заданной плоскости а, при

своем движении по направляющим обра-

зует поверхность цилиндроида, т. е. при

любом положении образующей должно

выполняться условие:

т'\\

а.

Проекции цилиндроида показаны на

рис. 227, где направляющие п и я

вместе

с плоскостью параллелизма Пз составляют

геометрическую часть определителя этой

поверхности.

Алгоритмическая часть содержит такую

последовательность операций:

обе направляющие пересекают плос-

костью а||П

;

находят точки А— п(]а и В = п*{]а;

строят прямую т, определяемую точка-

ми Л и В;

переходят к следующей плоскости ос'

и повторяют предыдущие операции.

Коноид и гиперболический параболоид

отличаются от цилиндроида лишь видом

направляющих, которые входят в набор

постоянных элементов геометрических час-

тей определителей рассматриваемых по-

верхностей.

Если криволинейная направляющая ко-

ноида плоская, то плоскость кривой не

должна совпадать с прямолинейной на-

правляющей.

Рис. 226

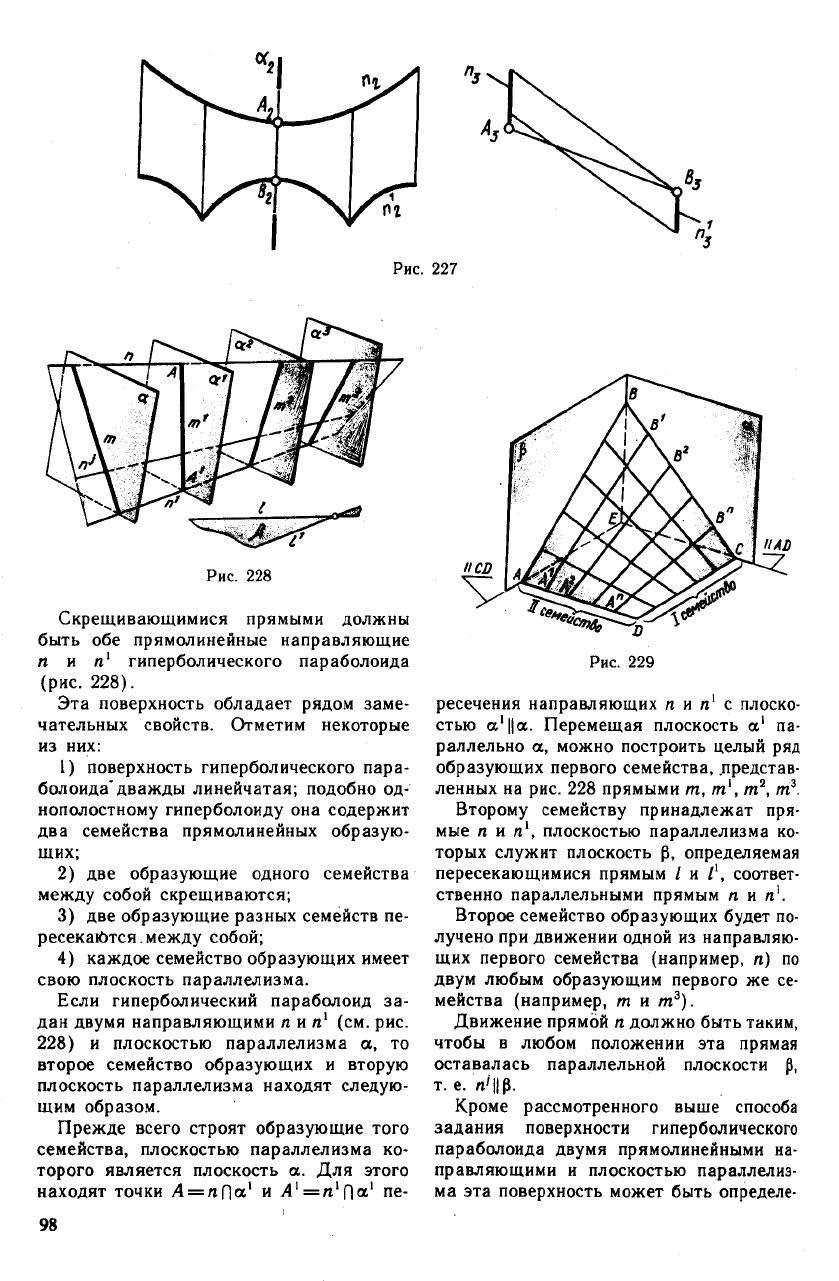
Скрещивающимися прямыми должны

быть обе прямолинейные направляющие

л и л

гиперболического параболоида

(рис. 228).

Эта поверхность обладает рядом заме-

чательных свойств. Отметим некоторые

из них:

1) поверхность гиперболического пара-

болоида' дважды линейчатая; подобно од-

нополостному гиперболоиду она содержит

два семейства прямолинейных образую-

щих;

2) две образующие одного семейства

между собой скрещиваются;

3) две образующие разных семейств пе-

ресекается. между собой;

4) каждое семейство образующих имеет

свою плоскость параллелизма.

Если гиперболический параболоид за-

дан двумя направляющими лип' (см. рис.

228) и плоскостью параллелизма а, то

второе семейство образующих и вторую

плоскость параллелизма находят следую-

щим образом.

Прежде всего строят образующие того

семейства, плоскостью параллелизма ко-

торого является плоскость а. Для этого

находят точки Л = лПа' и Л'=л'Па' пе-

ресечения направляющих л и л

с плоско-

стью а'||а. Перемещая плоскость а' па-

раллельно а, можно построить целый ряд

образующих первого семейства, представ-

ленных на рис. 228 прямыми т, т\ т

, т

Второму семейству принадлежат пря-

мые л и л

, плоскостью параллелизма ко-

торых служит плоскость (3, определяемая

пересекающимися прямым / и /', соответ-

ственно параллельными прямым л и п\

Второе семейство образующих будет по-

лучено при движении одной из направляю-

щих первого семейства (например, л) по

двум любым образующим первого же се-

мейства (например, т и /л

Движение прямой л должно быть таким,

чтобы в любом положении эта прямая

оставалась параллельной плоскости р,

т. е. я'|| р.

Кроме рассмотренного выше способа

задания поверхности гиперболического

параболоида двумя прямолинейными на-

правляющими и плоскостью параллелиз-

ма эта поверхность может быть определе-

на неплоским четырехугольни-

ком*.

Действительно, пусть дан неплоский че-

тырехугольник ABCD (рис. 229). Две про-

тивоположные стороны его, например АВ

и CD, можно принять в качестве направ-

ляющих, тогда две другие, AD и ВС, опре^

делят положение плоскости параллелизма.

На данном чертеже такой плоскостью яв-

ляется плоскость а, которая совмещена со

стороной ВС и прямой СЕ, причем послед-

няя параллельна AD.

Первое семейство образующих гипербо-

лического параболоида может быть созда-

но при движении стороны AD по принятым

за направляющие АВ и CD, когда прямая

AD остается параллельной плоскости а.

Второе семейство прямолинейных образу-

* Неплоским четырехугольником

называется четырехугольник, противоположные

стороны которого скрещиваются.

Рис. 230

ющих получится при движении АВ или

CD по двум другим противоположным сто-

ронам четырехугольника, в нашем слу-

чае — по AD и ВС, когда сторона АВ или

CD перемещается параллельно плоскости

Р", которая, являясь плоскостью паралле-

лизма, должна быть параллельной как АВ,

так и CD.

На рис. 229 плоскость р совмещена со

стороной АВ и проходит через прямую

AE\\CD. Образующими второго семейства

служат прямые АВ, Л'В

, А

А"В

CD.

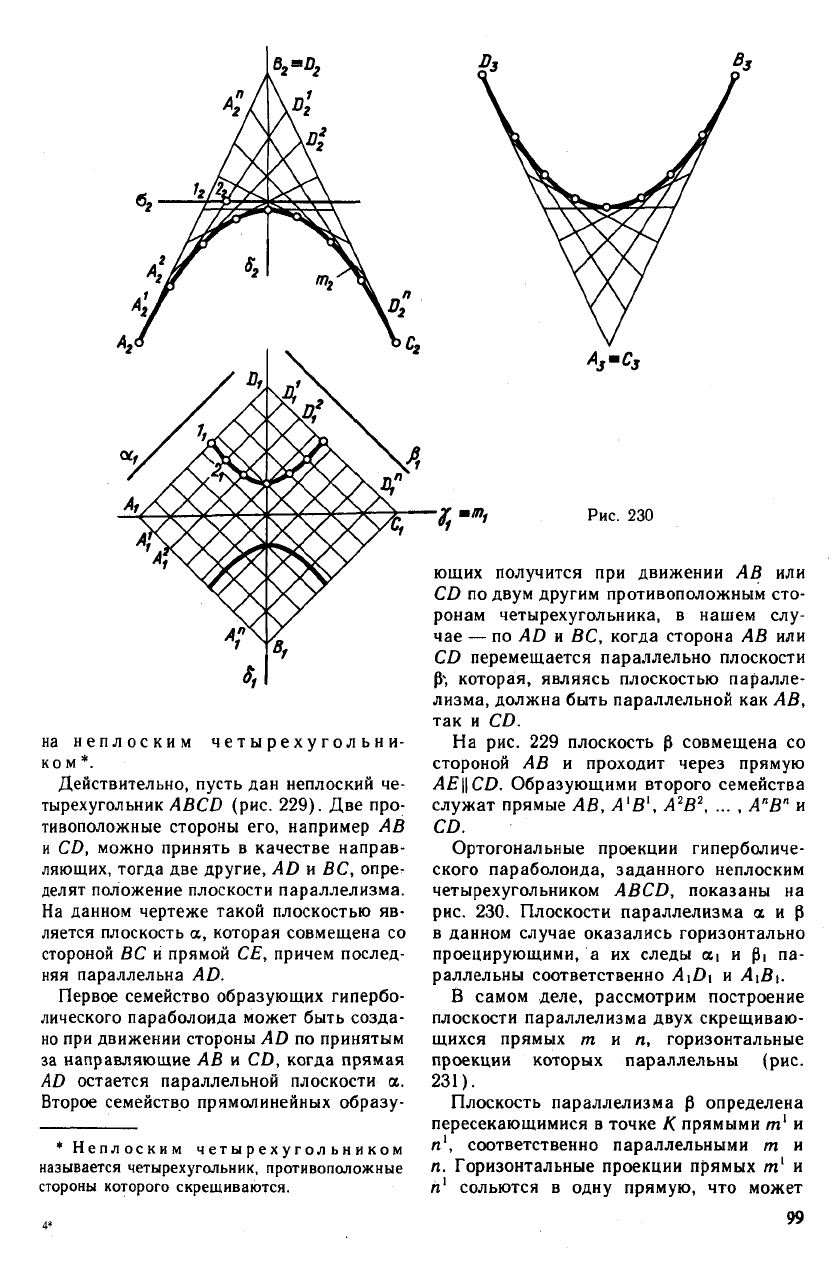
Ортогональные проекции гиперболиче-

ского параболоида, заданного неплоским

четырехугольником ABCD, показаны на

рис. 230. Плоскости параллелизма аир

в данном случае оказались горизонтально

проецирующими, а их следы ai и pi па-

раллельны соответственно J4iZ>i и А\В).

В самом деле, рассмотрим построение

плоскости параллелизма двух скрещиваю-

щихся прямых тип, горизонтальные

проекции которых параллельны (рис.

231).

Плоскость параллелизма р определена

пересекающимися в точке К прямыми т

п', соответственно параллельными т и

п. Горизонтальные проекции прямых т' и

/г

сольются в одну прямую, что может

4«