Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

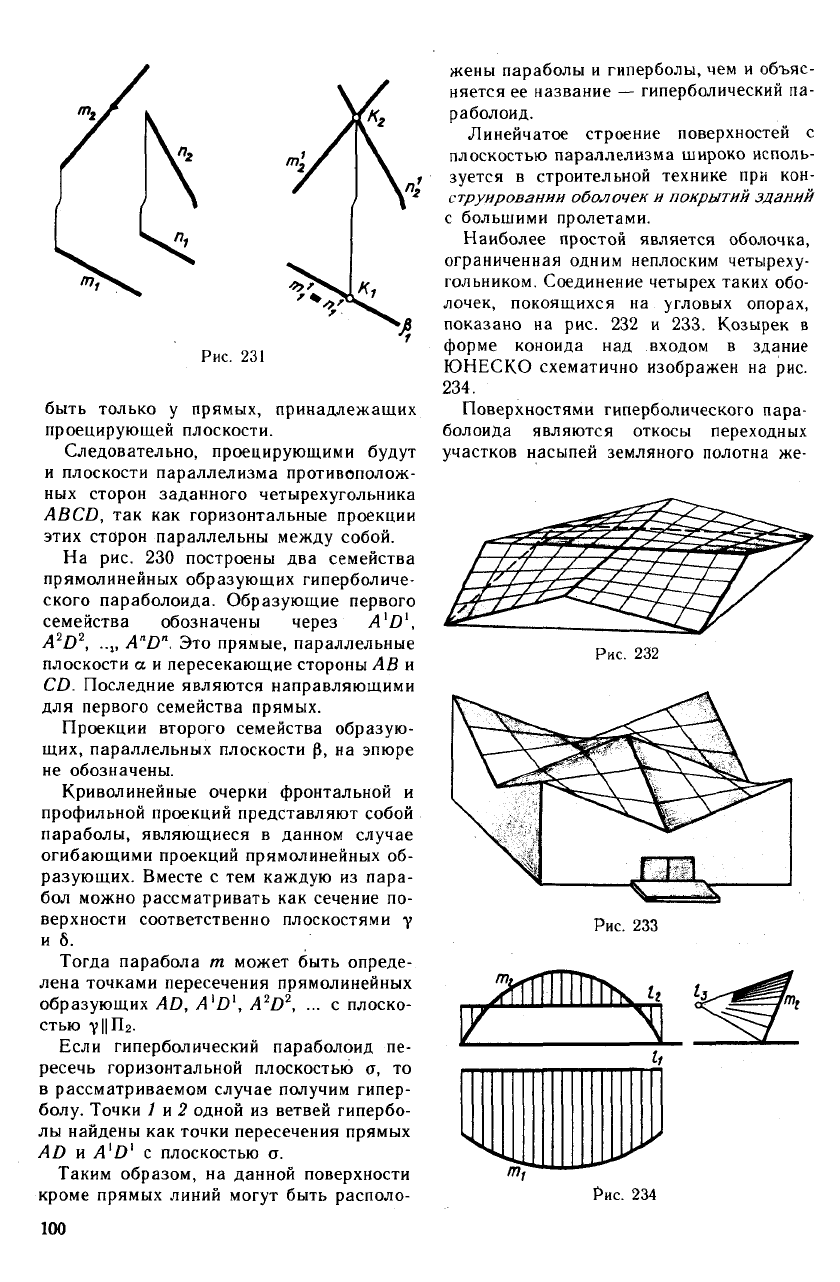
быть только у прямых, принадлежащих

проецирующей плоскости.

Следовательно, проецирующими будут

и плоскости параллелизма противополож-

ных сторон заданного четырехугольника

ABCD, так как горизонтальные проекции

этих сторон параллельны между собой.

На рис. 230 построены два семейства

прямолинейных образующих гиперболиче-

ского параболоида. Образующие первого

семейства обозначены через A

, ..„ A"D

, Это прямые, параллельные

плоскости а и пересекающие стороны АВ и

CD. Последние являются направляющими

для первого семейства прямых.

Проекции второго семейства образую-

щих, параллельных плоскости р, на эпюре

не обозначены.

Криволинейные очерки фронтальной и

профильной проекций представляют собой

параболы, являющиеся в данном случае

огибающими проекций прямолинейных об-

разующих. Вместе с тем каждую из пара-

бол можно рассматривать как сечение по-

верхности соответственно плоскостями у

и б.

Тогда парабола т может быть опреде-

лена точками пересечения прямолинейных

образующих AD, A

]

D\ A

, ... с плоско-

стью уЦПг-

Если гиперболический параболоид пе-

ресечь горизонтальной плоскостью а, то

в рассматриваемом случае получим гипер-

болу. Точки 1 и 2 одной из ветвей гипербо-

лы найдены как точки пересечения прямых

AD и A

D' с плоскостью а.

Таким образом, на данной поверхности

кроме прямых линий могут быть располо-

жены параболы и гиперболы, чем и объяс-

няется ее название — гиперболический па-

раболоид.

Линейчатое строение поверхностей с

плоскостью параллелизма широко исполь-

зуется в строительной технике при кон-

струировании оболочек и покрытий зданий

с большими пролетами.

Наиболее простой является оболочка,

ограниченная одним неплоским четыреху-

гольником. Соединение четырех таких обо-

лочек, покоящихся на угловых опорах,

показано на рис. 232 и 233. Козырек в

форме коноида над входом в здание

ЮНЕСКО схематично изображен на рис.

234.

Поверхностями гиперболического пара-

болоида являются откосы переходных

участков насыпей земляного полотна же-

«Г

Рис. 234

Рис. 231

100

лезной дороги. Такого рода переходы мо-

гут быть использованы при индивидуаль-

ном проектировании высоких пойменных

насыпей, уклон затопляемой части кото-

рых не должен быть круче 1:2 (рис. 235).

§ 46. ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИ

Циклическая поверхность образуется

при движении окружности постоянного

или переменного радиуса. Из большого

разнообразия способов построения одно-

параметрического множества окружно-

стей, представляющих собой каркасы рас-

сматриваемых поверхностей, выделим те,

которые отличаются общностью (универ-

сальностью) и конструктивной простотой.

Так как каркас циклических поверхно-

стей состоит из набора окружностей, ука-

жем вначале, какими геометрическими

элементами может быть определена ок-

ружность в пространстве:

1) тремя точками;

2) плоскостью, центром и величиной ра-

диуса;

3) двумя точками и прямой, располо-

женными в одной плоскости, при условии,

что эта прямая и центр окружности инци-

дентны;

4) тремя касательными;

5) сферой и пересекающей ее плоско-

стью;

6) вектором, начало которого совпадает

с центром окружности, направление пер-

пендикулярно плоскости окружности, а

модуль равен радиусу.

Этот перечень не исчерпывает все спосо-

бы задания окружности, но открывает

большие возможности для конструирова-

ния циклических поверхностей. Рассмот-

рим некоторые из них.

Первый способ (рис. 236).

Геометрическая часть определителя:

1) три направляющие т, /, я; 2) плос-

кость параллелизма а.

Алгоритмическая часть: 1) находим точ-

ки А, В, С пересечения направляющих

с плоскостью а', которая должна быть

параллельна а; 2) строим окружность,

определяемую тремя найденными точками;

3) переходим к следующей плоскости а

||а

и повторяем построения, описанные выше.

Второй способ (рис. 237).

Геометрическая часть определителя: 1)

две линии / и т, из которых одна является

линией центров; 2) ось i пучка плоскостей

или плоскость параллелизма р.

Алгоритмическая часть: 1) выделяем из

пучка плоскостей плоскость ос

; 2) нахо-

дим точки Л

и С

пересечения линий т и /

с плоскостью а

; 3) строим окружность

101

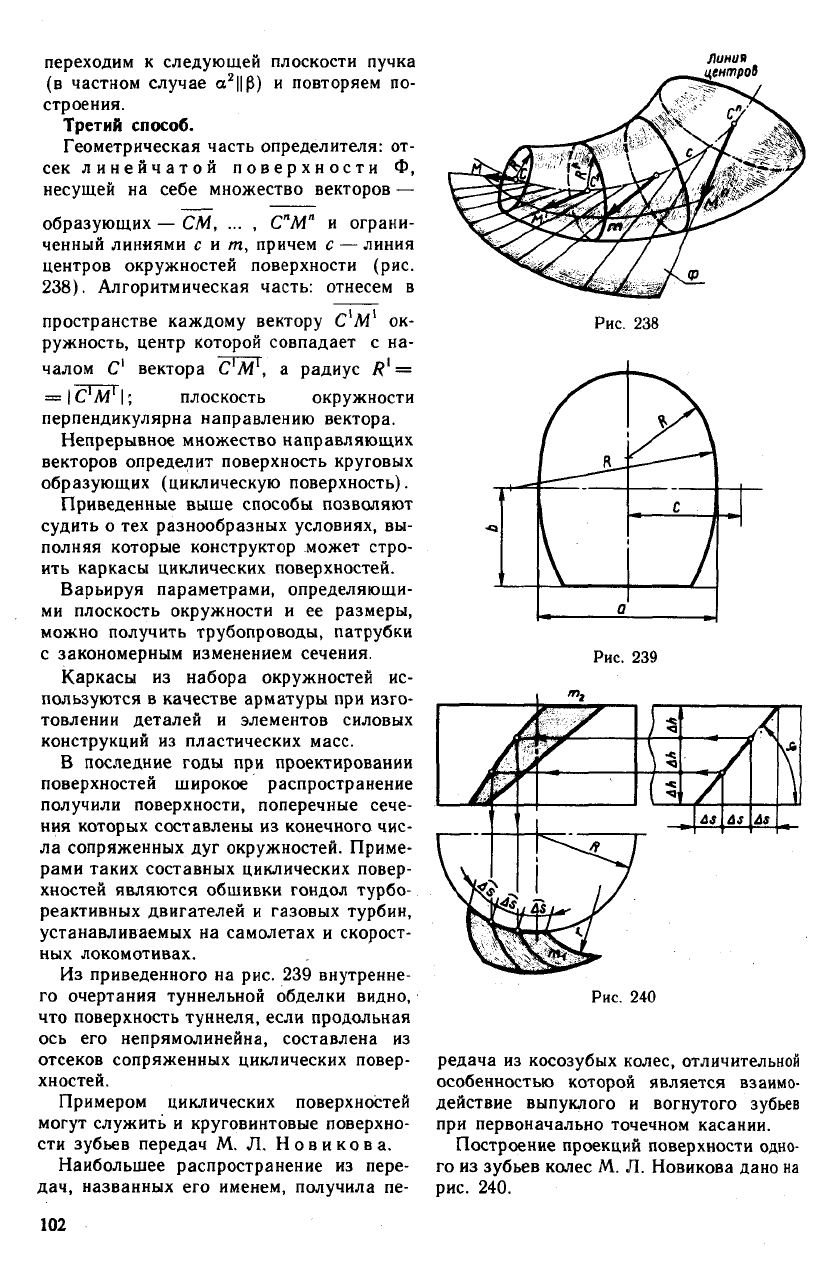
переходим к следующей плоскости пучка

(в частном случае а

||Р) и повторяем по-

строения.

Третий способ.

Геометрическая часть определителя: от-

сек линейчатой поверхности Ф,

несущей на себе множество векторов —

образующих — СМ СМ" и ограни-

ченный линиями сит, причем с — линия

центров окружностей поверхности (рис.

238). Алгоритмическая часть: отнесем в

Линия

центроб

пространстве каждому вектору С'УИ

ок-

ружность, центр которой совпадает с на-

чалом С' вектора С

, а радиус R

С'Л!

1; плоскость окружности

перпендикулярна направлению вектора.

Непрерывное множество направляющих

векторов определит поверхность круговых

образующих (циклическую поверхность).

Приведенные выше способы позволяют

судить о тех разнообразных условиях, вы-

полняя которые конструктор может стро-

ить каркасы циклических поверхностей.

Варьируя параметрами, определяющи-

ми плоскость окружности и ее размеры,

можно получить трубопроводы, патрубки

с закономерным изменением сечения.

Каркасы из набора окружностей ис-

пользуются в качестве арматуры при изго-

товлении деталей и элементов силовых

конструкций из пластических масс.

В последние годы при проектировании

поверхностей широкое распространение

получили поверхности, поперечные сече-

ния которых составлены из конечного чис-

ла сопряженных дуг окружностей. Приме-

рами таких составных циклических повер-

хностей являются обшивки гондол турбо-

реактивных двигателей и газовых турбин,

устанавливаемых на самолетах и скорост-

ных локомотивах.

Из приведенного на рис. 239 внутренне-

го очертания туннельной обделки видно,

что поверхность туннеля, если продольная

ось его непрямолинейна, составлена из

отсеков сопряженных циклических повер-

хностей.

Примером циклических поверхностей

могут служить и круговинтовые поверхно-

сти зубьев передач М. JT. Новикова.

Наибольшее распространение из пере-

дач, названных его именем, получила пе-

Рис. 238

Рис. 239

Рис. 240

редача из косозубых колес, отличительной

особенностью которой является взаимо-

действие выпуклого и вогнутого зубьев

при первоначально точечном касании.

Построение проекций поверхности одно-

го из зубьев колес М. Л. Новикова дано на

рис. 240.

102

Геометрическая часть определителя по-

верхности задана образующей т (дуга

окружности радиуса г), плоскостью па-

раллелизма П1 и углом ф наклона зубьев

на цилиндре радиуса R.

Алгоритмическая часть содержит всего

лишь указание на то, что образующая

т должна совершать винтовое движение

около оси цилиндра радиуса R.

Развертка винтовой линии, принадле-

жащей циклической поверхности радиуса

R, где угол ф изображается в натуральную

величину, позволяет установить переме-

щение As по дуге окружности радиуса R,

соответствующее прямолинейному переме-

щению Дh вдоль оси цилиндра.

Автор зубчатых передач с новой гео-

метрией М. Л. Новиков был удостоен в

1959 г. Государственной премии.

§ 47. ПОВЕРХНОСТИ

ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА

Поверхностью переноса называется по-

верхность, образуемая при поступатель-

ном перемещении одной кривой вдоль дру-

гой.

Напомним, что поступательное движе-

ние — такое движение фигуры (тела), при

котором перемещения всех точек ее за

любой промежуток времени параллельны

и имеют од.'у и ту же величину.

Любая прямая, которая принадлежит

фигуре, совершающей поступательное

движение, перемещается, оставаясь па-

раллельной самой себе.

Геометрическая часть определителя по-

верхности переноса состоит из двух кри-

вых линий: образующей m и направляю-

щей п (рис. 241).

Алгоритмическая часть содержит следу-

ющий перечень операций, связанных с по-

строением каркаса поверхности:

1) на направляющей п намечаем ряд

точек А, В, С, ... ;

2) строим векторы АВ, ВС, ... ;

3) осуществляем параллельный перенос

линии т; переносы задаются векторами

АВ, ВС, ... .

Поверхности параллельного переноса

отвечают важному технологическому тре-

бованию — их можно формировать при

помощи передвижной опалубки. с*то до-

Рис. 242

стоинство их и используется при создании

монолитных и сборных оболочек.

Проекции каркаса оболочки, направля-

ющая которой п, образующая — пг, пока-

заны на рис. 242.

Покажем, что поверхность переноса мо-

жет быть представлена уравнением

Я =

(ы)+ф (у), . (8.35)

где ф и — векторы-функции, завися-

щие соответственно от и и v, причем и яв-

ляется параметром, к которому отнесена

образующая m, a v — параметр, фиксиру-

ющий точку на направляющей п.

Радиус-вектор точки М (см. рис. 241),

принадлежащей поверхности Ф, предста-

вим в виде

Я = (8.36)

где ОК = г (и)—радиус-вектор точки

К^т,

т. е. первое слагаемое выражения (8.36)

представляет собой вектор-функцию пара-

метра и, второе — вектор-функцию, зави-

сящую только от V.

Из параллелограмма АВМК следует,

что одну и ту же точку М поверхности

переноса можно получить, перемещая об-

разующую по направляющей или, наобо-

103

рот,— направляющую по образующей.

Линии тип, которыми задается повер-

хность параллельного переноса, обратимы.

Вопросы и задачи для самоконтроля

1. Что называется определителем поверхно-

сти и из каких двух частей он состоит?

2. Из каких геометрических фигур состоит

геометрическая часть определителя линейчатых

поверхностей с плоскостью параллелизма?

3. Составить алгоритмическую часть опреде-

лителя поверхности, которая образуется движе-

нием прямой линии по трем скрещивающимся

прямым.

4. Какая поверхность однозначно определя-

ется заданием одной пространственной кривой

линии?

5. Какие поверхности образуют семейства

плоскостей, касающихся двух непересекающих-

ся сфер?

6. Какую поверхность образует множество

конгруэнтных окружностей, имеющих общую

хорду? общую касательную?

7. Какие поверхности формируются ребрами

куба при его вращении вокруг одной из диаго-

налей?

8. Какие поверхности сформирует конус при

вращении около оси г, с которой ось конуса

пересекается под углом 30°, а угол при вершине

конуса равен 30° (60°)? Вершина конуса распо-

ложена на оси г.

9. Циклическая поверхность задана линией

центров, одной направляющей и плоскостью,

параллельно которой должна оставаться плос-

кость движущейся окружности. Составить алго-

ритмическую часть определителя этой повер-

хности.

10. Как образуется винтовая поверхность?

Запишите ее определитель.

11. Как задается и формируется поверхность

параллельного переноса?

ГЛАВА 9

ПОЗИЦИОННЫЕ ЗАДАЧИ

НА ПОВЕРХНОСТИ

$ 48. ЛИНИИ И ТОЧКИ,

ПРИНАДЛЕЖАЩИЕ ПОВЕРХНОСТИ

Покажем полезность принятого понятия

каркаса и его эффективность. Убедимся,

что множество линий, заполняющих по-

верхность, позволяет решить любую пози-

ционную задачу независимо от строения

самой поверхности.

•

Рис. 243

Задача 1. Построение линии, принадле-

жащей поверхности.

Предполагается, что одна из проекций

линии задана. Так, на рис. 243 изображе-

на горизонтальная т\ проекция линии,

которая принадлежит поверхности Ф.

Здесь и в дальнейшем будем считать за-

данными проекции каркаса — линии /',

, ... . Требуется построить фронтальную

проекцию т.2 линии т.

Отметим точки 11, 2\, ... , в которых

горизонтальные проекции линий каркаса

пересекаются с одноименной проекцией

заданной линии. С помощью линий про-

екционной связи находим фронтальные

проекции /

, 2% ... тех же точек и соеди-

няем их лекальной кривой.

Задача 2. По одной проекции точки,

принадлежащей поверхности, построить ее

вторую проекцию. -

План решения задачи:

1) строим каркас поверхности; 2) через

заданную проекцию точки проводим одно-

именную проекцию вспомогательной ли-

нии, принадлежащей поверхности и пе-

ресекающей каркас образующих; 3) стро-

им вторую проекцию вспомогательной

кривой, на которой и определяем с по-

мощью линии связи искомую проекцию

точки.

Эта последовательность построений и

была реализована на рис. 243, где резуль-

татом решения является фронтальная про-

екция Кг точки К (/СеФ).

104

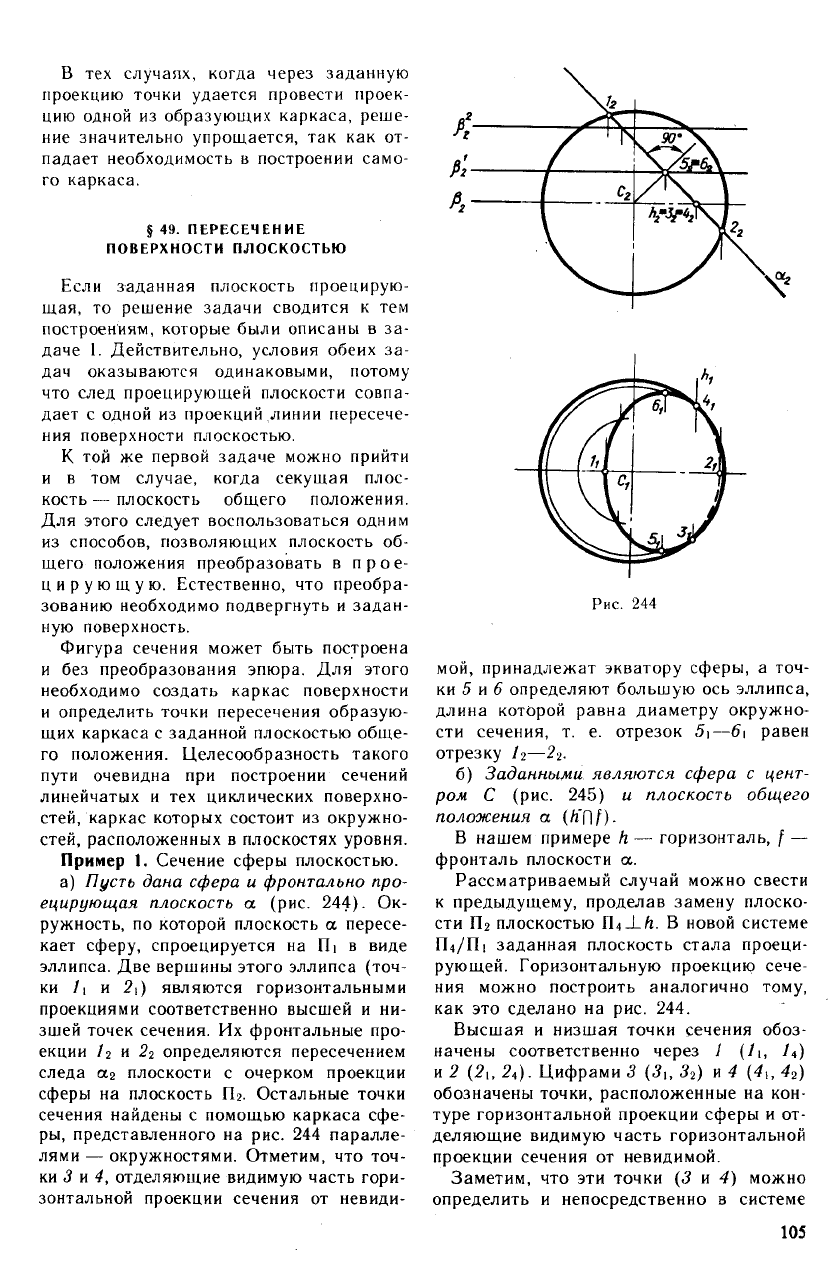
В тех случаях, когда через заданную

проекцию точки удается провести проек-

цию одной из образующих каркаса, реше-

ние значительно упрощается, так как от-

падает необходимость в построении само-

го каркаса.

§ 49. ПЕРЕСЕЧЕНИЕ

ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

Если заданная плоскость проецирую-

щая, то решение задачи сводится к тем

построениям, которые были описаны в за-

даче 1. Действительно, условия обеих за-

дач оказываются одинаковыми, потому

что след проецирующей плоскости совпа-

дает с одной из проекций линии пересече-

ния поверхности плоскостью.

К той же первой задаче можно прийти

и в том случае, когда секущая плос-

кость — плоскость общего положения.

Для этого следует воспользоваться одним

из способов, позволяющих плоскость об-

щего положения преобразовать в прое-

цирующую. Естественно, что преобра-

зованию необходимо подвергнуть и задан-

ную поверхность.

Фигура сечения может быть построена

и без преобразования эпюра. Для этого

необходимо создать каркас поверхности

и определить точки пересечения образую-

щих каркаса с заданной плоскостью обще-

го положения. Целесообразность такого

пути очевидна при построении сечений

линейчатых и тех циклических поверхно-

стей, каркас которых состоит из окружно-

стей, расположенных в плоскостях уровня.

Пример 1. Сечение сферы плоскостью.

а) Пусть дана сфера и фронтально про-

ецирующая плоскость а (рис. 244). Ок-

ружность, по которой плоскость а пересе-

кает сферу, спроецируется на П| в виде

эллипса. Две вершины этого эллипса (точ-

ки 11 и 21) являются горизонтальными

проекциями соответственно высшей и ни-

зшей точек сечения. Их фронтальные про-

екции /г и 2

определяются пересечением

следа аг плоскости с очерком проекции

сферы на плоскость Пг. Остальные точки

сечения найдены с помощью каркаса сфе-

ры, представленного на рис. 244 паралле-

лями — окружностями. Отметим, что точ-

ки 3 и 4, отделяющие видимую часть гори-

зонтальной проекции сечения от невиди-

мой, принадлежат экватору сферы, а точ-

ки 5 и б определяют большую ось эллипса,

длина которой равна диаметру окружно-

сти сечения, т. е. отрезок 5\—61 равен

отрезку /

—2

б) Заданными являются сфера с цент-

ром С (рис. 245) и плоскость общего

положения a (h'(]j).

В нашем примере h — горизонталь, f —

фронталь плоскости а.

Рассматриваемый случай можно свести

к предыдущему, проделав замену плоско-

сти Пг плоскостью П

В новой системе

П4/П1 заданная плоскость стала проеци-

рующей. Горизонтальную проекцию сече-

ния можно построить аналогично тому,

как это сделано на рис. 244.

Высшая и низшая точки сечения обоз-

начены соответственно через 1 (1\, /

)

и 2 (2

). Цифрами 3 (З

) и 4 {4

)

обозначены точки, расположенные на кон-

туре горизонтальной проекции сферы и от-

деляющие видимую часть горизонтальной

проекции сечения от невидимой.

Заметим, что эти точки (3 и 4) можно

определить и непосредственно в системе

105

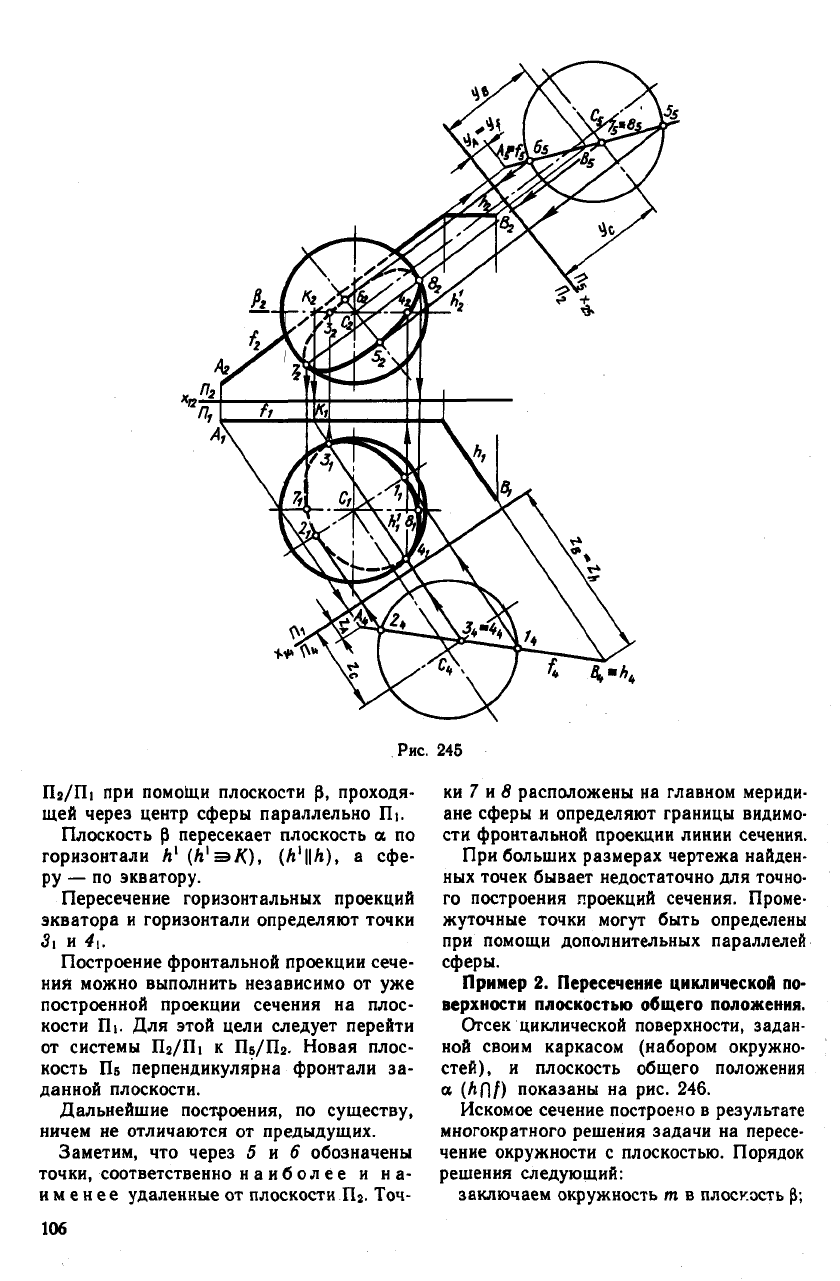
Рис. 245

П2/П1 при помо1ци плоскости р, проходя-

щей через центр сферы параллельно П|.

Плоскость р пересекает плоскость а по

горизонтали А

(А'э/С), (А'||А), а сфе-

ру — по экватору.

Пересечение горизонтальных проекций

экватора и горизонтали определяют точки

31 и 4,.

Построение фронтальной проекции сече-

ния можно выполнить независимо от уже

построенной проекции сечения на плос-

кости Ш. Для этой цели следует перейти

от системы П2/П1 к П5/П2. Новая плос-

кость Пб перпендикулярна фронтали за-

данной плоскости.

Дальнейшие построения, по существу,

ничем не отличаются от предыдущих.

Заметим, что через 5 и 6 обозначены

точки, соответственно наиболее и на-

именее удаленные от плоскости П5. Точ-

ки 7 и 8 расположены на главном мериди-

ане сферы и определяют границы видимо-

сти фронтальной проекции линии сечения.

При больших размерах чертежа найден-

ных точек бывает недостаточно для точно-

го построения проекций сечения. Проме-

жуточные точки могут быть определены

при помощи дополнительных параллелей

сферы.

Пример 2. Пересечение циклической по-

верхности плоскостью общего положения.

Отсек циклической поверхности, задан-

ной своим каркасом (набором окружно-

стей), и плоскость общего положения

a (Af)/) показаны на рис. 246.

Искомое сечение построено в результате

многократного решения задачи на пересе-

чение окружности с плоскостью. Порядок

решения следующий:

заключаем окружность т в плоскость Р;

106

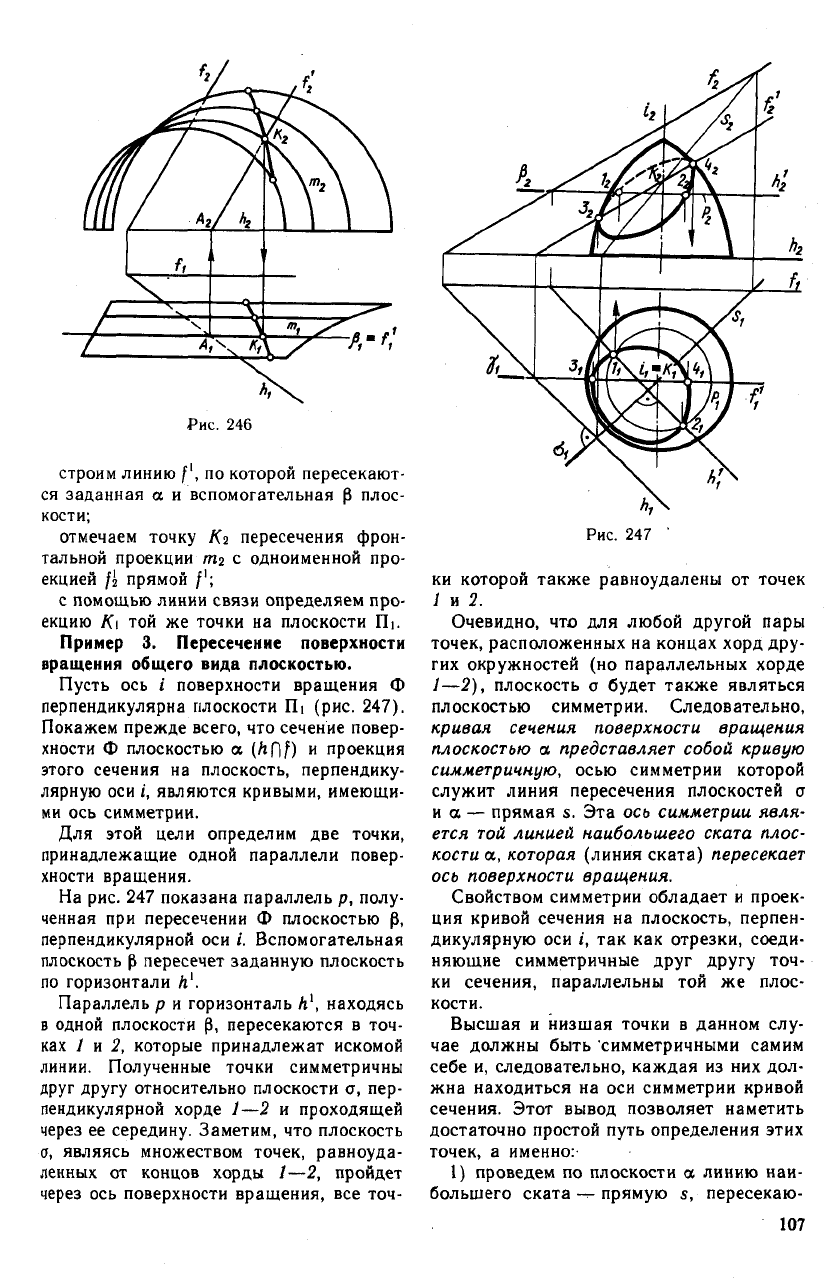
строим линию f', по которой пересекают-

ся заданная а и вспомогательная р плос-

кости;

отмечаем точку Кг пересечения фрон-

тальной проекции тг с одноименной про-

екцией {1 прямой /';

с помощью линии связи определяем про-

екцию КI той же точки на плоскости Пь

Пример 3. Пересечение поверхности

вращения общего вида плоскостью.

Пусть ось i поверхности вращения Ф

перпендикулярна плоскости П] (рис. 247).

Покажем прежде всего, что сечение повер-

хности Ф плоскостью а (ЛOf) и проекция

этого сечения на плоскость, перпендику-

лярную оси 1, являются кривыми, имеющи-

ми ось симметрии.

Для этой цели определим две точки,

принадлежащие одной параллели повер-

хности вращения.

На рис. 247 показана параллель р, полу-

ченная при пересечении Ф плоскостью р,

перпендикулярной оси I. Вспомогательная

плоскость р пересечет заданную плоскость

по горизонтали А

Параллель р и горизонталь А

, находясь

в одной плоскости р, пересекаются в точ-

ках / и 2, которые принадлежат искомой

линии. Полученные точки симметричны

друг другу относительно плоскости а, пер-

пендикулярной хорде 1—2 и проходящей

через ее середину. Заметим, что плоскость

о, являясь множеством точек, равноуда-

ленных от концов хорды /—2, пройдет

через ось поверхности вращения, все точ-

ки которой также равноудалены от точек

/ и 2.

Очевидно, что для любой другой пары

точек, расположенных на концах хорд дру-

гих окружностей (но параллельных хорде

1—2), плоскость о будет также являться

плоскостью симметрии. Следовательно,

кривая сечения поверхности вращения

плоскостью а представляет собой кривую

симметричную, осью симметрии которой

служит линия пересечения плоскостей ст

и а — прямая s. Эта ось симметрии явля-

ется той линией наибольшего ската плос-

кости а, которая (линия ската) пересекает

ось поверхности вращения.

Свойством симметрии обладает и проек-

ция кривой сечения на плоскость, перпен-

дикулярную оси i, так как отрезки, соеди-

няющие симметричные друг другу точ-

ки сечения, параллельны той же плос-

кости.

Высшая и низшая точки в данном слу-

чае должны быть симметричными самим

себе и, следовательно, каждая из них дол-

жна находиться на оси симметрии кривой

сечения. Этот вывод позволяет наметить

достаточно простой путь определения этих

точек, а именно:

1) проведем по плоскости а линию наи-

большего ската прямую s, пересекаю-

107

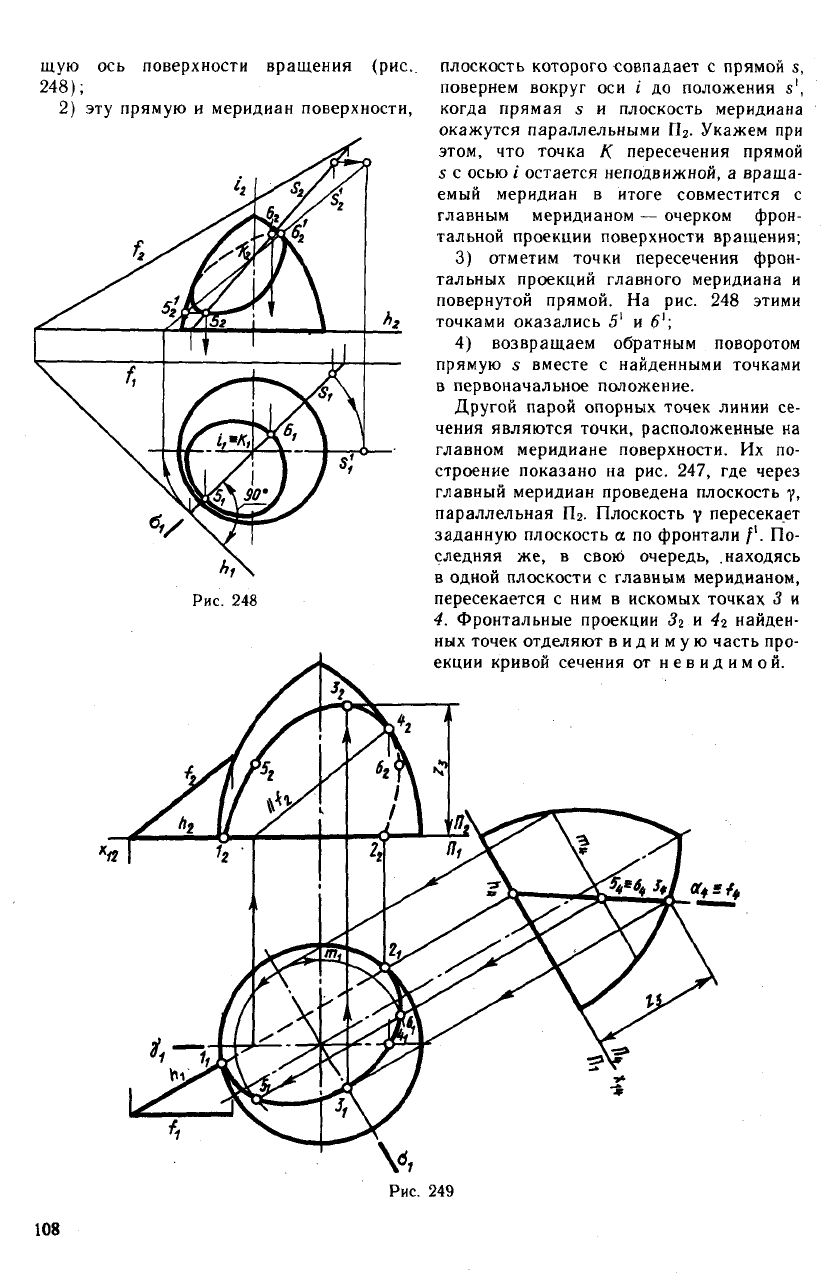
щую

248);

2) эту прямую и меридиан поверхности,

ось поверхности вращения (рис.. плоскость которого совпадает с прямой s,

повернем вокруг оси i до положения s

когда прямая s и плоскость меридиана

окажутся параллельными Г1

. Укажем при

этом, что точка К пересечения прямой

5 с осью i остается неподвижной, а враща-

емый меридиан в итоге совместится с

главным меридианом — очерком фрон-

тальной проекции поверхности вращения;

3) отметим точки пересечения фрон-

тальных проекций главного меридиана и

повернутой прямой. На рис. 248 этими

точками оказались 5

и 6';

4) возвращаем обратным поворотом

прямую 5 вместе с найденными точками

в первоначальное положение.

Другой парой опорных точек линии се-

чения являются точки, расположенные на

главном меридиане поверхности. Их по-

строение показано на рис. 247, где через

главный меридиан проведена плоскость у,

параллельная Пг. Плоскость у пересекает

заданную плоскость а по фронтали По-

следняя же, в свою очередь, .находясь

в одной плоскости с главным меридианом,

пересекается с ним в искомых точках 3 и

4. Фронтальные проекции ЗГ и 4Г найден-

ных точек отделяют видимую часть про-

екции кривой сечения от невидимой.

Рис. 248

108

На рис. 249 приведено решение по су-

ществу такой же задачи с использованием

способа замены плоскостей проекций, ког-

да плоскость a (f(]h) общего положения

была преобразована в проецирующую. Ее

след а

на плоскости 11

является вместе

с тем и вырожденной проекцией сечения

заданной поверхности тора.

Заметим, что в данном примере новая

плоскость проекций П

параллельна а —

общей плоскости симметрии заданных по-

верхностей (тора и плоскости а). Каркас

тора на рис. 249 представлен всего лишь

одной параллелью т, которая в точках

5 и 6 пересекается с плоскостью а. С по-

мощью плоскости у, параллельной П

проходящей через ось тора, найдена точка

4, отделяющая видимую часть фронталь-

ной проекции сечения от невидимой.

Пример 4. Конические сечения.

На рис. 250 изображены три сечения

прямого кругового конуса * различными

плоскостями. Докажем, что:

1) если секущая плоскость не парал-

лельна ни одной из образующих конуса, то

в сечении получается эллипс (рис. 250, а)

2) если секущая плоскость параллельна

только одной образующей, то в сечении

будет парабола (рис. 250, б);

3) если пересечь конус плоскостью,

параллельной двум его образующим (в

частном случае параллельно оси кону-

са), то в сечении получится гипербола

(рис. 250, в).

Для доказательства справедливости

этих утверждений повторим стереометри-

ческие рассуждения бельгийского мате-

матика Данделенома (1794—1887), кото-

рый использовал факт равенства отрезков,

касательных к сфере, проведенных из од-

ной точки. Это факт позволил ему устано-

вить фокальные и директориальные свой-

ства конических сечений.

Итак, пусть плоскость а (рис. 251 и 252)

пересекает все образующие конуса по кри-

вой /. Впишем в конус две сферы с центра-

ми О

и О

, касающиеся секущей плоско-

сти а в точках F

и F

. Обозначим через

тип окружности, по которым сферы

* Конус, у которого основанием является

круг, называется прямым, если высота его

проходит через центр основания, в ином случае

конус называется наклонным.

касаются конуса. Возьмем на кривой /

произвольную точку М и покажем, что

+MF

= const. Для этого проведем

через точку М образующую MS и отметим

точки Л и В, в которых эта образующая

касается сфер. Отрезки MF

и МЛ равны,

так как они касаются сферы с центром

в точке О'. На том же основании можно

утверждать, что MF

= MB. Но МЛ +

+ МВ — длина отрезка образующей, ог-

раниченной двумя параллелями тип ко-

нуса, а потому эта сумма постоянна. По-

стоянна будет и сумма отрезков М/

' и

MF\

Следовательно, коническое сечение /

представляет собой множество точек, сум-

ма расстояний которых от двух данных

точек F' и F

есть величина постоянная.

Это фокальное свойство присуще только

эллипсу.

Аналогично Доказывается фокальное

свойство для гиперболы (рис. 253) с той

лишь разницей, что сферы располагаются

в различных полостях конуса. В этом слу-

чае коническим сечением будет множество

точек М, разность расстояний которых от

двух точек F

и F

есть величина посто-

янная. В принятых на рис. 253 обозначе-

ниях MF

-MF

=AB.

Рассмотрим, наконец, сечение конуса

плоскостью а, параллельной одной обра-

зующей конуса (рис. 254). На этот раз

впишем в конус сферу, касающуюся плос-

кости-а в точке F, а конуса — по окружно-

сти т, расположенной в плоскости р. По-

кажем, что для любой точки'М коническо-

го сечения справедливо равенство MF =

= MN, в котором отрезок MN перпендику-

лярен прямой d пересечения плоскостей а

109