Крылов Н.Н., ред. Начертательная геометрия
Подождите немного. Документ загружается.

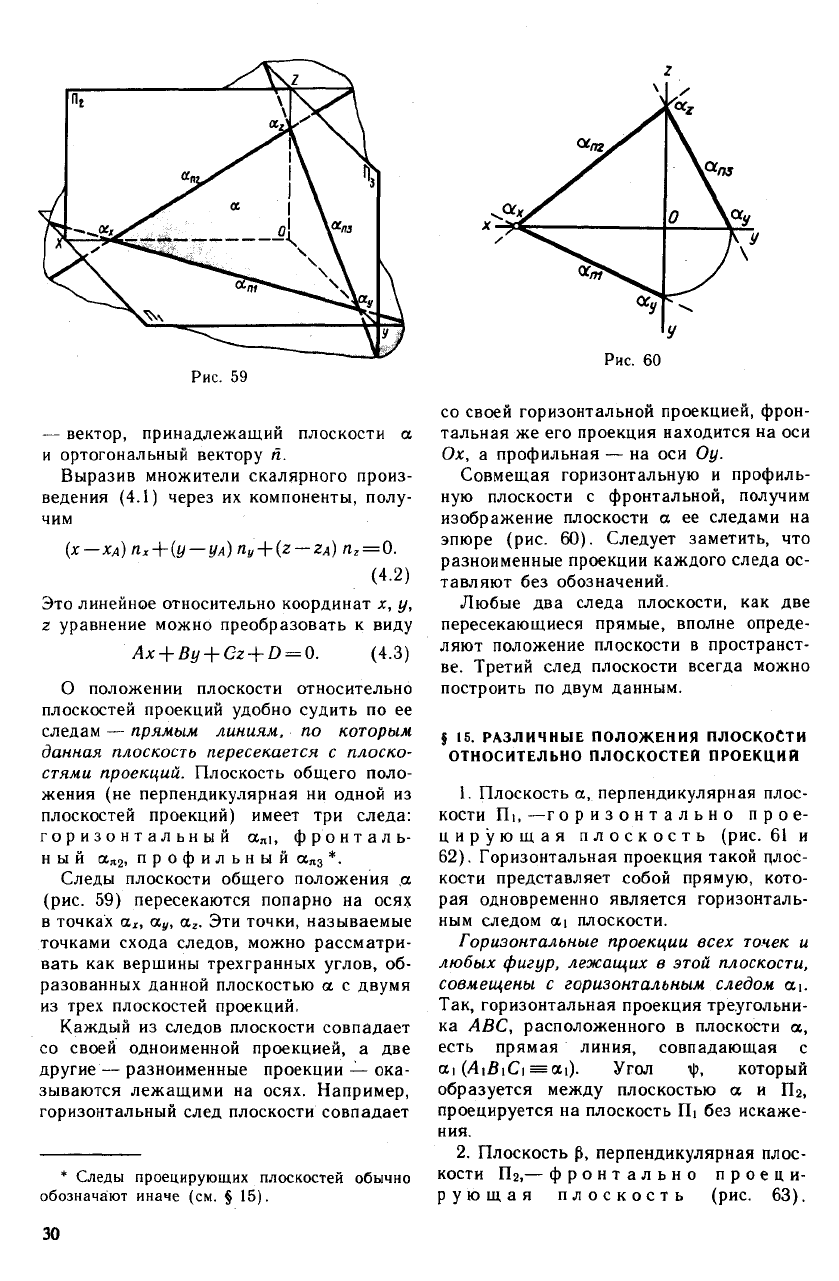
Рис. 59
— вектор, принадлежащий плоскости а
и ортогональный вектору п.
Выразив множители скалярного произ-
ведения (4.1) через их компоненты, полу-
чим
(Х—Х
А
)П
Х
+ (У —
УА) NY
+ (Z — Z
A
) л
г
= 0.
(4.2)
Это линейное относительно координат х, у,
г уравнение можно преобразовать к виду
Ax + By +
C-z
+ D = 0. (4.3)
О положении плоскости относительно
плоскостей проекций удобно судить по ее
следам — прямым линиям, по которым
данная плоскость пересекается с плоско-
стями проекций. Плоскость общего поло-
жения (не перпендикулярная ни одной из
плоскостей проекций) имеет три следа:
горизонтальный а
л
ь фронталь-
ный а„
2
, профильный а„
3
*.
Следы плоскости общего положения а
(рис. 59) пересекаются попарно на осях
в точках а*, а
у
, а*. Эти точки, называемые
точками схода следов, можно рассматри-
вать как вершины трехгранных углов, об-
разованных данной плоскостью а с двумя
из трех плоскостей проекций.
Каждый из следов плоскости совпадает
со своей одноименной проекцией, а две
другие — разноименные проекции — ока-
зываются лежащими на осях. Например,
горизонтальный след плоскости совпадает
* Следы проецирующих плоскостей обычно
обозначают иначе (см. § 15).
Рис. 60
со своей горизонтальной проекцией, фрон-
тальная же его проекция находится на оси
Ох, а профильная — на оси Оу.
Совмещая горизонтальную и профиль-
ную плоскости с фронтальной, получим
изображение плоскости а ее следами на
эпюре (рис. 60). Следует заметить, что
разноименные проекции каждого следа ос-
тавляют без обозначений.
Любые два следа плоскости, как две
пересекающиеся прямые, вполне опреде-
ляют положение плоскости в пространст-
ве. Третий след плоскости всегда можно
построить по двум данным.
§ 15. РАЗЛИЧНЫЕ ПОЛОЖЕНИЯ ПЛОСКОСТИ
ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
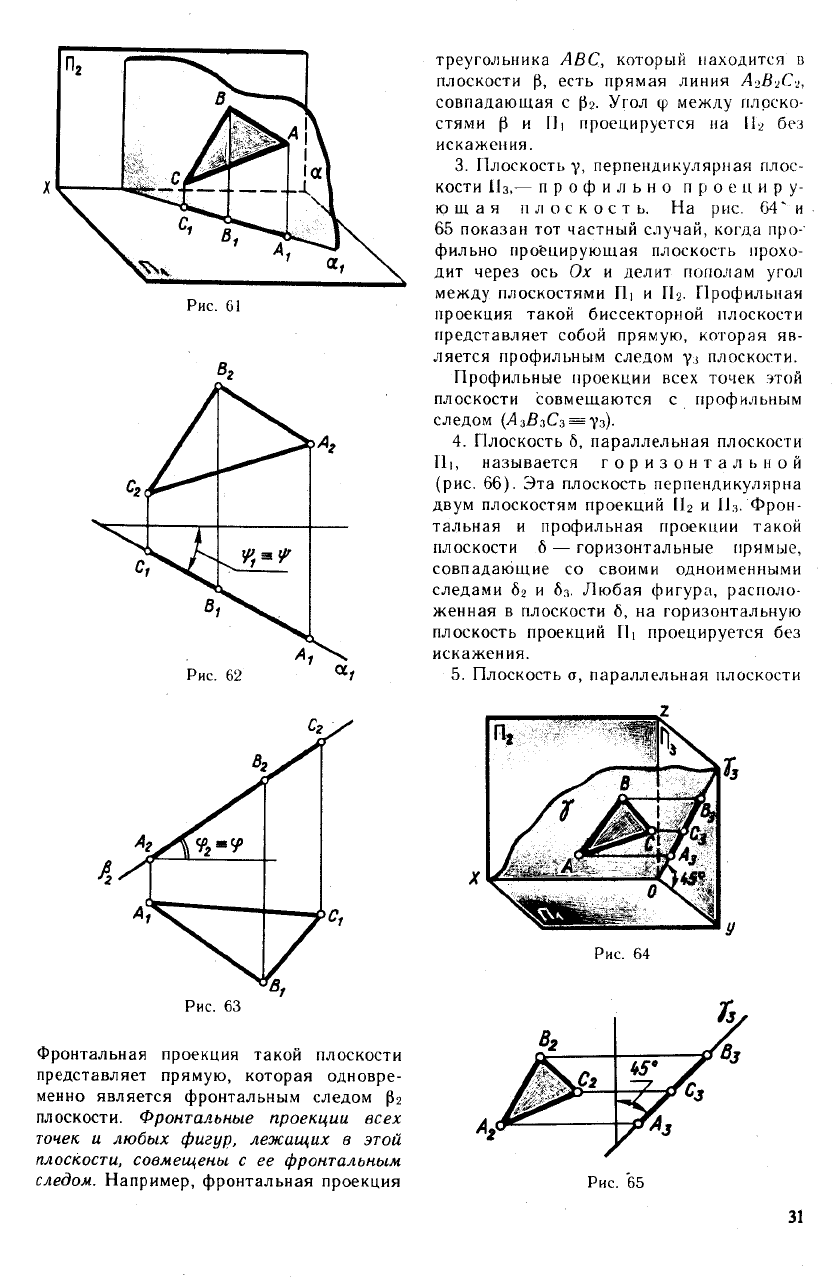
1. Плоскость а, перпендикулярная плос-
кости Пь —г оризонтально прое-
цирующая плоскость (рис. 61 и
62). Горизонтальная проекция такой плос-
кости представляет собой прямую, кото-
рая одновременно является горизонталь-
ным следом ai плоскости.
Горизонтальные проекции всех точек и
любых фигур, лежащих в этой плоскости,
совмещены с горизонтальным следом а\.
Так, горизонтальная проекция треугольни-
ка ABC, расположенного в плоскости а,
есть прямая линия, совпадающая с
ai (А\В\С\ =<*i). Угол г|>, который
образуется между плоскостью а и Пг,
проецируется на плоскость без искаже-
ния.
2. Плоскость р, перпендикулярная плос-
кости П
2
,— фронтально проеци-
рующая плоскость (рис. 63).
30
Ci
В,
S^v
Рис.
61
/
в
г
/
>
)А
г
А-
С
В
Рис. 62
треугольника ABC, который находится в
плоскости (5, есть прямая линия А^В^С?,
совпадающая с fb- Угол ф между плоско-
стями р и 111 проецируется на lb без
искажения.
3. Плоскость у, перпендикулярная плос-
кости Из,— профильно проециру-
ющая плоскость. На рис. 64" и
65 показан тот частный случай, когда про-
фильно проецирующая плоскость прохо-
дит через ось Ох и делит пополам угол
между плоскостями Tli и ГЬ. Профильная
проекция такой биссекторной плоскости
представляет собой прямую, которая яв-
ляется профильным следом уз плоскости.
Профильные проекции всех точек этой
плоскости совмещаются с профильным
следом (ЛзВ
3
Сз = 7з).
4. Плоскость б, параллельная плоскости
Hi, называется горизонтальной
(рис. 66). Эта плоскость перпендикулярна
двум плоскостям проекций Пг и И
3
. Фрон-
тальная и профильная проекции такой
плоскости б — горизонтальные прямые,
совпадающие со своими одноименными
следами 62 и 63. Любая фигура, располо-
женная в плоскости б, на горизонтальную
плоскость проекций Hi проецируется без
искажения.
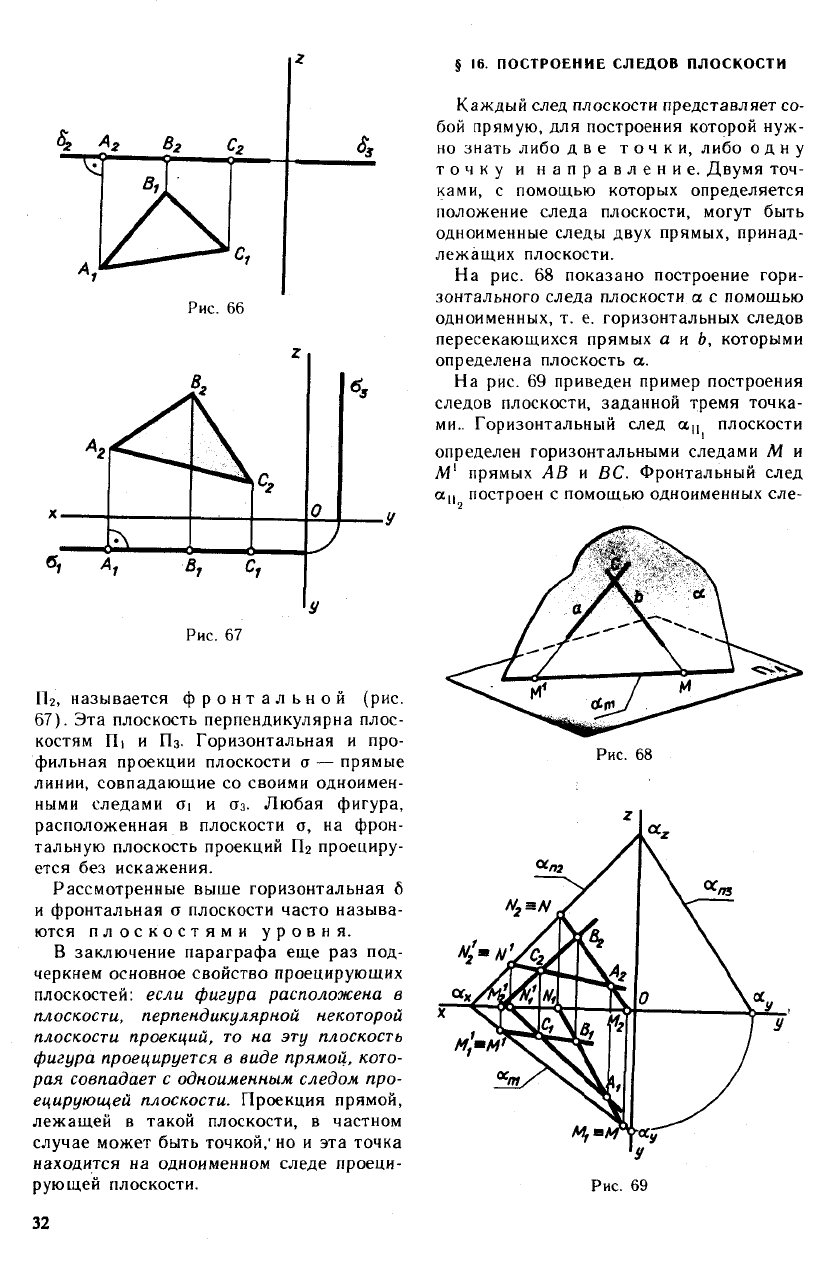
5. Плоскость а, параллельная плоскости
Рис. 63
Фронтальная проекция такой плоскости
представляет прямую, которая одновре-
менно является фронтальным следом р
2
плоскости. Фронтальные проекции всех
точек и любых фигур, лежащих в этой
плоскости, совмещены с ее фронтальным
следом. Например, фронтальная проекция
Рис. 64
Рис. 65
31
г
§ 16. ПОСТРОЕНИЕ СЛЕДОВ ПЛОСКОСТИ
с—_
0
J
S А, В, С,
и
Рис. 67
Пг, называется фронтальной (рис.
67). Эта плоскость перпендикулярна плос-
костям П| и Пз. Горизонтальная и про-
фильная проекции плоскости а — прямые
линии, совпадающие со своими одноимен-
ными следами о\ и сгз. Любая фигура,
расположенная в плоскости а, на фрон-
тальную плоскость проекций Пг проециру-
ется без искажения.
Рассмотренные выше горизонтальная б
и фронтальная а плоскости часто называ-
ются плоскостями уровня.
В заключение параграфа еще раз под-
черкнем основное свойство проецирующих
плоскостей: если фигура расположена в
плоскости, перпендикулярной некоторой
плоскости проекций, то на эту плоскость
фигура проецируется в виде прямой, кото-
рая совпадает с одноименным следом про-
ецирующей плоскости. Проекция прямой,
лежащей в такой плоскости, в частном
случае может быть точкой,' но и эта точка
находится на одноименном следе проеци-
рующей плоскости.
Каждый след плоскости представляет со-
бой прямую, для построения которой нуж-
но знать либо две точки, либо одну
точку и направление. Двумя точ-
ками, с помощью которых определяется
положение следа плоскости, могут быть
одноименные следы двух прямых, принад-
лежащих плоскости.
На рис. 68 показано построение гори-
зонтального следа плоскости а с помощью
одноименных, т. е. горизонтальных следов
пересекающихся прямых а и Ь, которыми
определена плоскость а.
На рис. 69 приведен пример построения
следов плоскости, заданной тремя точка-
ми.. Горизонтальный след а
П1
плоскости
определен горизонтальными следами М и
М' прямых АВ и ВС. Фронтальный след
а
и
построен с помощью одноименных сле-
32
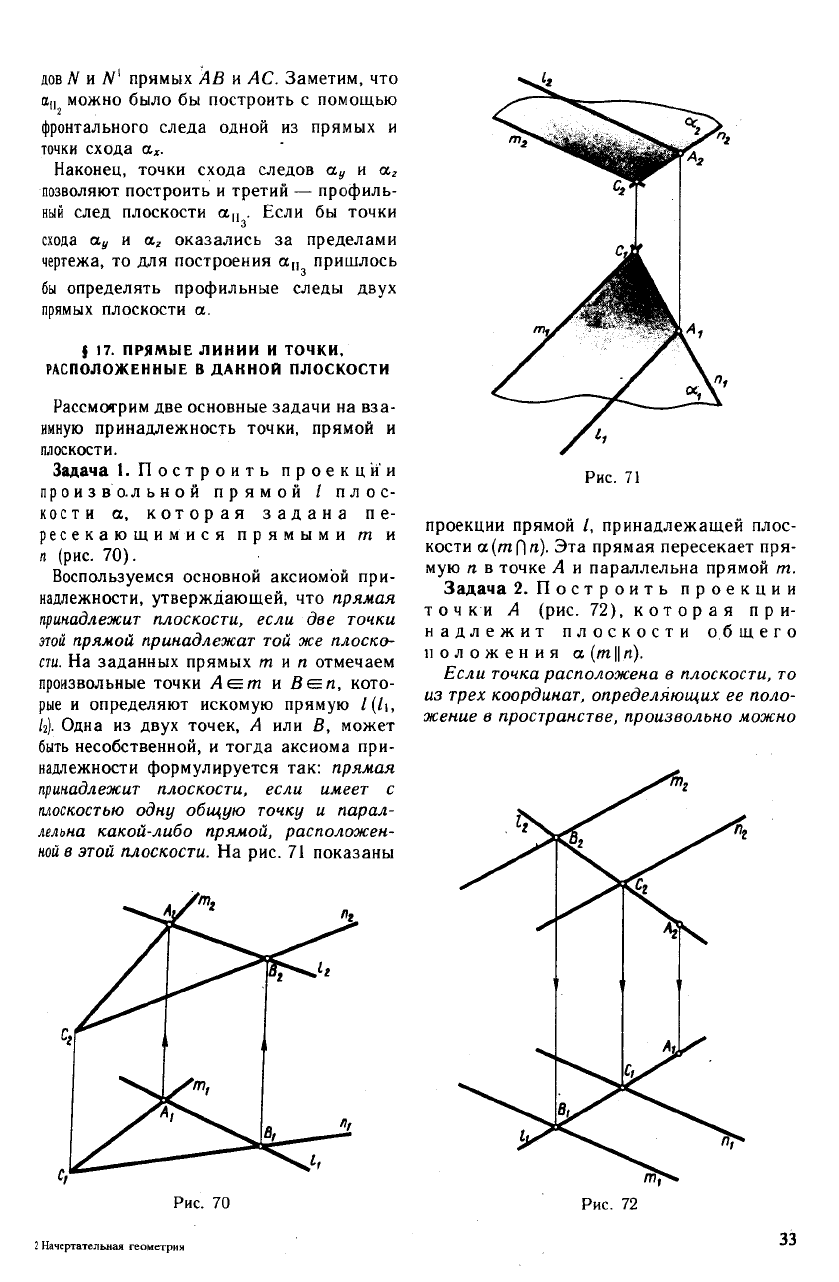
дов N и N
i
прямых АВ и АС. Заметим, что
d|] можно было бы построить с помощью
фронтального следа одной из прямых и
точки схода а*.
Наконец, точки схода следов а
у
и а
г
позволяют построить и третий — профиль-
ный след плоскости а,, . Если бы точки
"з
схода а
у
и а
г
оказались за пределами
чертежа, то для построения сс
п
пришлось
бы определять профильные следы двух
прямых плоскости а.
f 17. ПРЯМЫЕ ЛИНИИ И ТОЧКИ.
РАСПОЛОЖЕННЫЕ В ДАННОЙ ПЛОСКОСТИ
Рассмотрим две основные задачи на вза-
имную принадлежность точки, прямой и
плоскости.
Задача 1. Построить проекции
произвольной прямой I плос-
кости а, которая задана пе-
ресекающимися прямыми т и
п (рис. 70).
Воспользуемся основной аксиомой при-
надлежности, утверждающей, что прямая
принадлежит
плоскости, если две точки
этой
прямой принадлежат той же плоско-
сти.
На заданных прямых тип отмечаем
произвольные точки Лет и Ben, кото-
рые и определяют искомую прямую 1{1\,
1г).
Одна из двух точек, А или В, может
быть несобственной, и тогда аксиома при-
надлежности формулируется так: прямая
принадлежит плоскости, если имеет с
плоскостью одну общую точку и парал-
лельна какой-либо прямой, расположен-
ной
в этой плоскости. На рис. 71 показаны
2 Начертательная геометрия
Рис. 71
проекции прямой I, принадлежащей плос-
кости а(т[\п). Эта прямая пересекает пря-
мую п в точке А и параллельна прямой т.
Задача 2. Построить проекции
точки А (рис. 72), которая при-
надлежит плоскости общего
положения а
(т\\п).
Если
точка
расположена в плоскости, то
из трех координат, определяющих ее поло-
жение в пространстве, произвольно можно
33
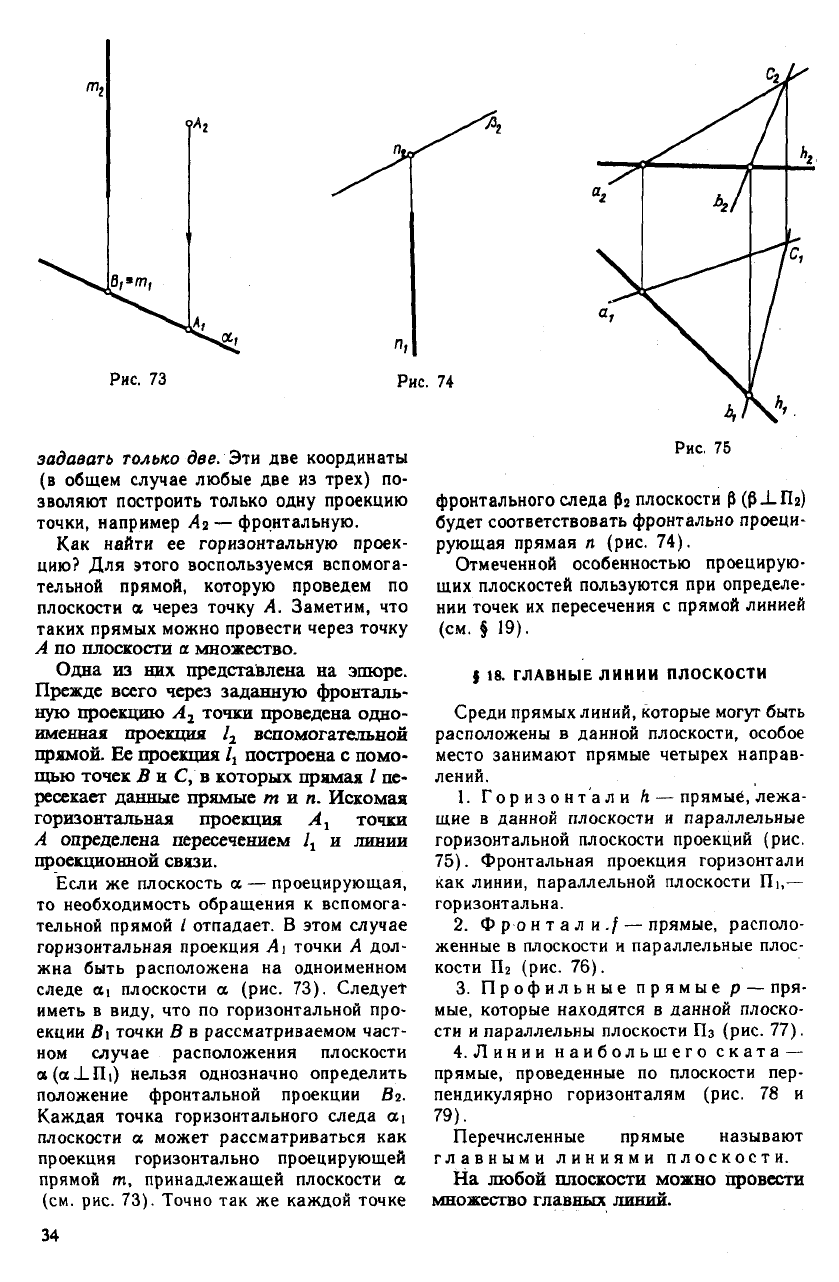
Рис. 73
Рис. 74
задавать только две. Эти две координаты
(в общем случае любые две из трех) по-
зволяют построить только одну проекцию
точки, например А2 — фронтальную.
Как найти ее горизонтальную проек-
цию? Для этого воспользуемся вспомога-
тельной прямой, которую проведем по
плоскости а через точку А. Заметим, что
таких прямых можно провести через точку
А по плоскости а множество.
Одна из них представлена на эпюре.
Прежде всего через заданную фронталь-
ную проекцию А
г
точки проведена одно-
именная проекция /
2
вспомогательной
прямой. Ее проекция построена с помо-
щью точек В к С, в которых прямая / пе-
ресекает данные прямые тип. Искомая
горизонтальная проекция А
1
точки
А определена пересечением и линии
проекционной связи.
Если же плоскость а — проецирующая,
то необходимость обращения к вспомога-
тельной прямой I отпадает. В этом случае
горизонтальная проекция Ai точки А дол-
жна быть расположена на одноименном
следе си плоскости а (рис. 73). Следует
иметь в виду, что по горизонтальной про-
екции В\ точки В в рассматриваемом част-
ном случае расположения плоскости
a(a_l_ni) нельзя однозначно определить
положение фронтальной проекции Вч.
Каждая точка горизонтального следа ai
плоскости а может рассматриваться как
проекция горизонтально проецирующей
прямой т, принадлежащей плоскости a
(см. рис. 73). Точно так же каждой точке
Рис. 75
фронтального следа (Ь плоскости 0
(($
_1_Пг)
будет соответствовать фронтально проеци-
рующая прямая л (рис. 74).
Отмеченной особенностью проецирую-
щих плоскостей пользуются при определе-
нии точек их пересечения с прямой линией
(см. § 19).
f 18. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Среди прямых линий, которые могут быть
расположены в данной плоскости, особое
место занимают прямые четырех направ-
лений.
1. Горизонтали h — прямыё, лежа-
щие в данной плоскости и параллельные
горизонтальной плоскости проекций (рис.
75). Фронтальная проекция горизонтали
как линии, параллельной плоскости Пь—
горизонтальна.
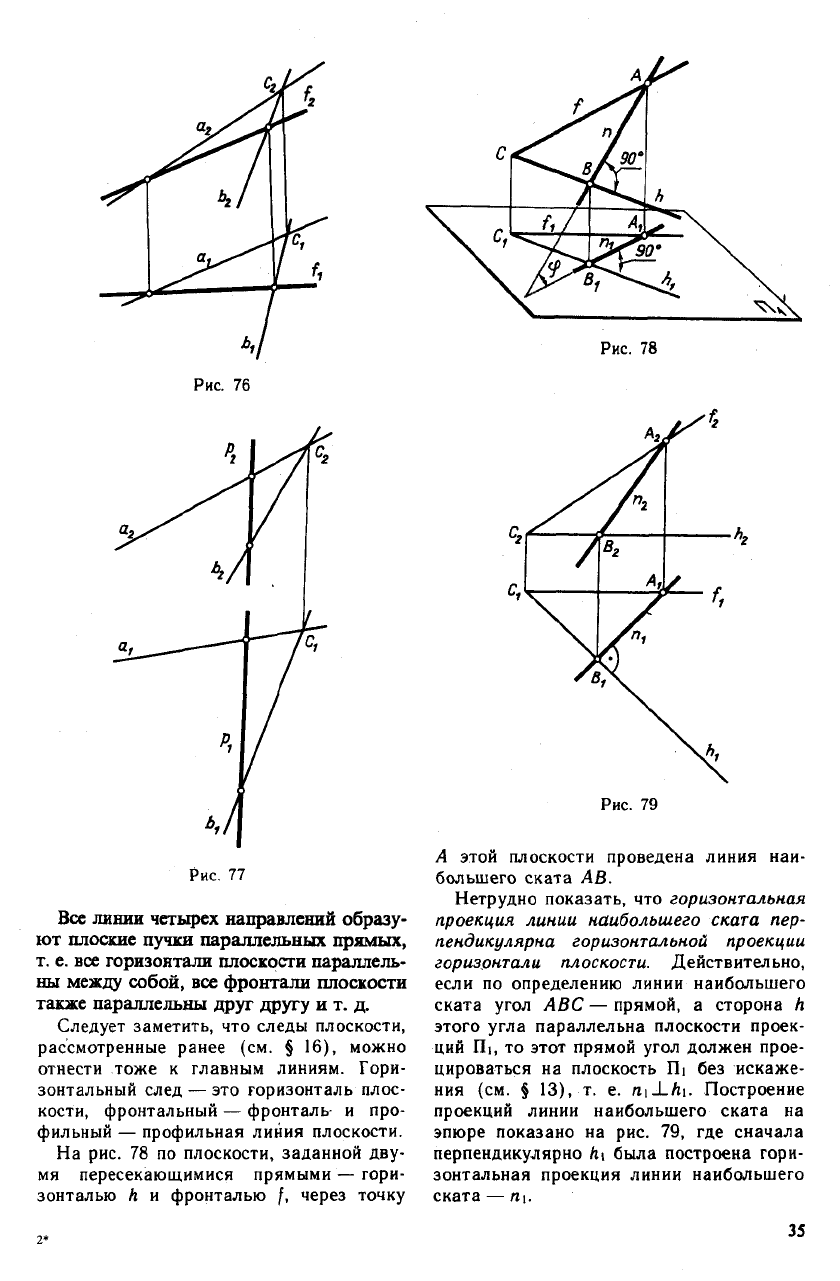
2. Фронтали./ — прямые, располо-
женные в плоскости и параллельные плос-
кости Пг (рис. 76).
3. Профильные прямые р— пря-
мые, которые находятся в данной плоско-
сти и параллельны плоскости Пз (рис. 77).
4. Линии наибольшего ската —
прямые, проведенные по плоскости пер-
пендикулярно горизонталям (рис. 78 и
79).
Перечисленные прямые называют
главными линиями плоскости.
На любой плоскости можно провести
множество главных линий.
34
4
Рис. 76
Рис. 78
Все линии четырех направлений образу-
ют плоские пучки параллельных прямых,
т. е. все горизонтали плоскости параллель-
ны между собой, все фронтали плоскости
также параллельны друг другу и т. д.
Следует заметить, что следы плоскости,
рассмотренные ранее (см. § 16), можно
отнести тоже к главным линиям. Гори-
зонтальный след — это горизонталь плос-
кости, фронтальный — фронталь- и про-
фильный — профильная линия плоскости.
На рис. 78 по плоскости, заданной дву-
мя пересекающимися прямыми — гори-
зонталью h и фронталью f, через точку
А этой плоскости проведена линия наи-
большего ската АВ.
Нетрудно показать, что горизонтальная
проекция линии наибольшего ската пер-
пендикулярна горизонтальной проекции
горизонтали плоскости. Действительно,
если по определению линии наибольшего
ската угол ABC — прямой, а сторона h
этого угла параллельна плоскости проек-
ций П1, то этот прямой угол должен прое-
цироваться на плоскость Иi без искаже-
ния (см. § 13), т. е. m-LAi. Построение
проекций линии наибольшего ската на
эпюре показано на рис. 79, где сначала
перпендикулярно h\ была построена гори-
зонтальная проекция линии наибольшего
ската — п\.
2*
35
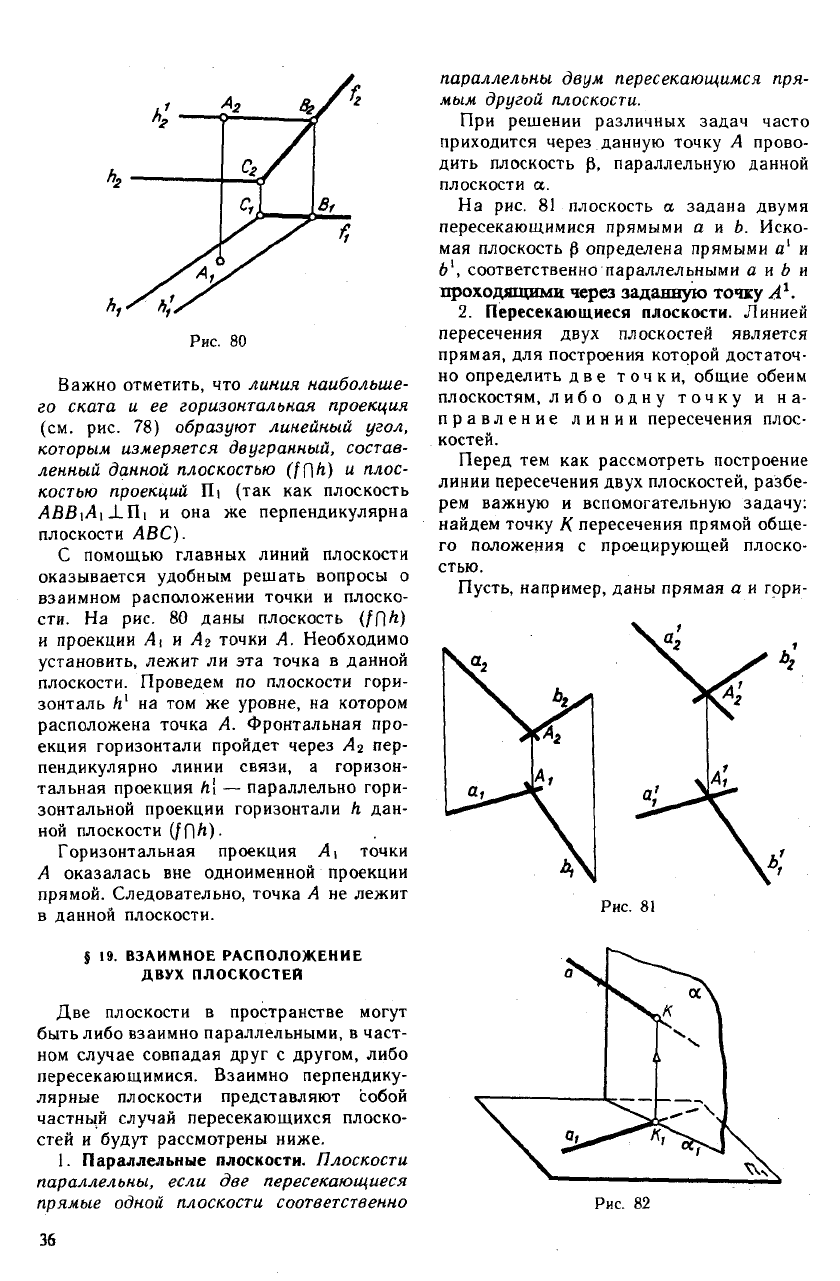
Рис. 80
Важно отметить, что линия наибольше-
го ската и ее горизонтальная проекция
(см. рис. 78) образуют линейный угол,
которым измеряется двугранный, состав-
ленный данной плоскостью (ff\h) и плос-
костью проекций П1 (так как плоскость
y4BfMi-LIIi и она же перпендикулярна
плоскости ABC).
С помощью главных линий плоскости
оказывается удобным решать вопросы о
взаимном расположении точки и плоско-
сти. На рис. 80 даны плоскость (/П^)
и проекции А, и Аг точки А. Необходимо
установить, лежит ли эта точка в данной
плоскости. Проведем по плоскости гори-
зонталь ft
1
на том же уровне, на котором
расположена точка А. Фронтальная про-
екция горизонтали пройдет через Лг пер-
пендикулярно линии связи, а горизон-
тальная проекция h\ — параллельно гори-
зонтальной проекции горизонтали h дан-
ной плоскости {fflh).
Горизонтальная проекция A
i
точки
А оказалась вне одноименной проекции
прямой. Следовательно, точка А не лежит
в данной плоскости.
параллельны двум пересекающимся пря-
мым другой плоскости.
При решении различных задач часто
приходится через данную точку А прово-
дить плоскость р, параллельную данной
плоскости а.
На рис. 81 плоскость а задана двумя
пересекающимися прямыми а и Ь. Иско-
мая плоскость р определена прямыми а
1
и
6', соответственно параллельными а и b и
проходящими через заданную точку А
1
.
2. Пересекающиеся плоскости. Линией
пересечения двух плоскостей является
прямая, для построения которой достаточ-
но определить две точки, общие обеим
плоскостям, л и б о одну точку и на-
правление линии пересечения плос-
костей.
Перед тем как рассмотреть построение
линии пересечения двух плоскостей, разбе-
рем важную и вспомогательную задачу:
найдем точку К пересечения прямой обще-
го положения с проецирующей плоско-
стью.
Пусть, например, даны прямая а и гори-
Рис. 81
§ 19. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПЛОСКОСТЕЙ
Две плоскости в пространстве могут
быть либо взаимно параллельными, в част-
ном случае совпадая друг с другом, либо
пересекающимися. Взаимно перпендику-
лярные плоскости представляют собой
частный случай пересекающихся плоско-
стей и будут рассмотрены ниже.
1. Параллельные плоскости. Плоскости
параллельны, если две пересекающиеся
прямые одной плоскости соответственно
Рис. 131 Рис.
132
Рис. 133
36

зонтально проецирующая плоскость а
(рис. 82). Тогда горизонтальная проекция
К\ искомой точки должна одновременно
лежать на горизонтальной проекции ai
плоскости а и на горизонтальной проекции
а
1
прямой а, т. е. в точке пересечения а\
с ai (/Ci=aif]ai) (рис. 83). Фронтальная
проекция К<2 точки К расположена на ли-
нии проекционной связи и на фронтальной
проекции <22 прямой а.
А теперь разберем один из частных слу-
чаев пересекающихся плоскостей, когда
одна из них — проецирующая.
На рис. 84 приведены плоскость общего
положения, заданная треугольником ABC,
и горизонтально проецирующая плоскость
а. Найдем две общие точки для этих двух
плоскостей. Очевидно, этими общими точ-
ками для плоскостей Л ABC и а будут
точки пересечения сторон АВ и ВС треу-
гольника ABC с проецирующей плоско-
стью а. Построение таких точек D и Е как
на пространственном чертеже (рис. 84),
так и на эпюре (рис. 85) не вызывает
затруднений после разобранного выше
примера.
Соединяя одноименные проекции точек
D и Е, получим проекции линии пересече-
ния плоскости АABC и плоскости а.
Таким образом, горизонтальная проек-
ция D\E\ линии пересечения заданных
плоскостей совпадает с горизонтальной
проекцией проецирующей плоскости a —
с ее горизонтальным следом а\.
Рассмотрим теперь общий случай.
Пусть в пространстве заданы две плоско-
сти общего положения аир (рис. 86).
Для построения линии их пересечения не-
обходимо, как отмечалось выше, найти две
точки, общие обеим плоскостям.
Для определения этих точек заданные
37
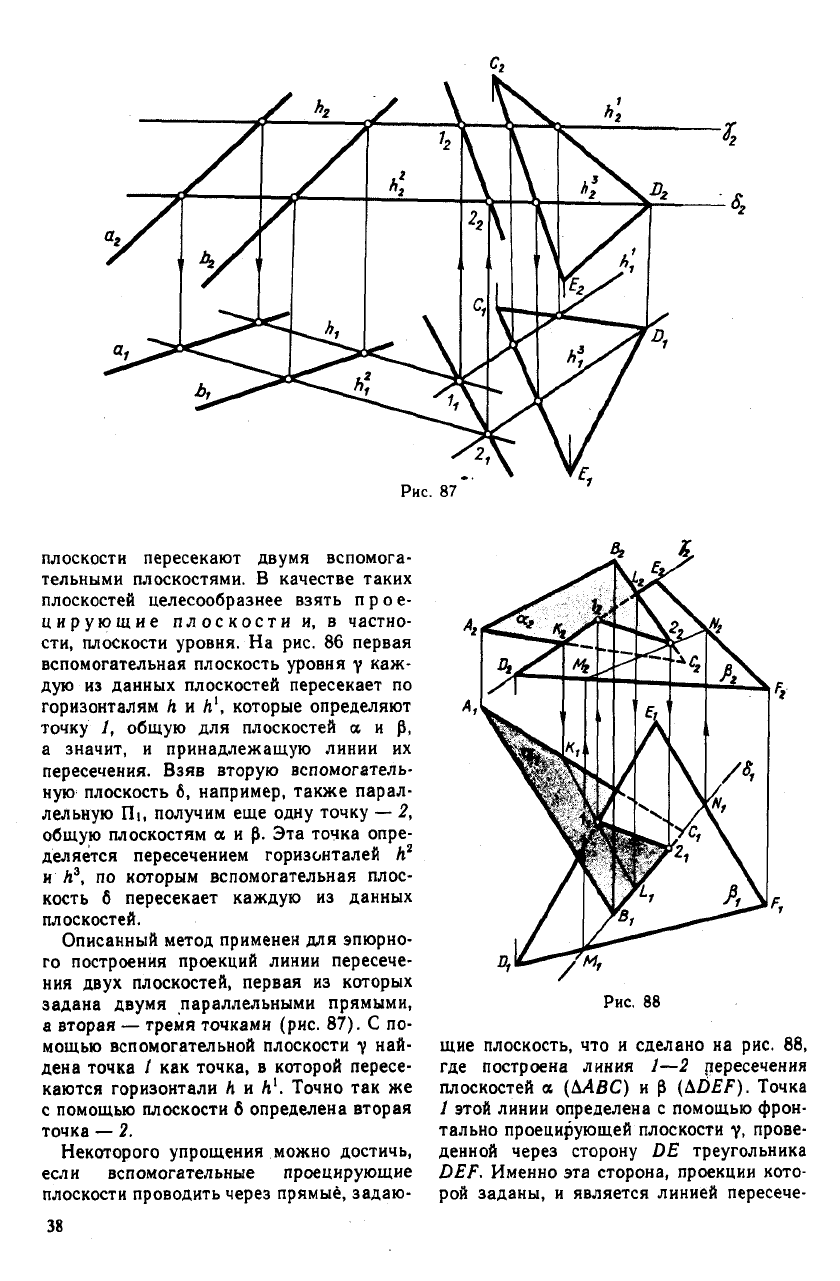
плоскости пересекают двумя вспомога-
тельными плоскостями. В качестве таких
плоскостей целесообразнее взять прое-
цирующие плоскости и, в частно-
сти, плоскости уровня. На рис. 86 первая
вспомогательная плоскость уровня у каж-
дую из данных плоскостей пересекает по
горизонталям Л и А
1
, которые определяют
точку 1, общую для плоскостей аир,
а значит, и принадлежащую линии их
пересечения. Взяв вторую вспомогатель-
ную плоскость 6, например, также парал-
лельную III, получим еще одну точку — 2,
общую плоскостям аир. Эта точка опре-
деляется пересечением горизонталей Л
2
и А
3
, по которым вспомогательная плос-
кость 6 пересекает каждую из данных
плоскостей.
Описанный метод применен для эпюрно-
го построения проекций линии пересече-
ния двух плоскостей, первая из которых
задана двумя параллельными прямыми,
а вторая — тремя точками (рис. 87). С по-
мощью вспомогательной плоскости v най-
дена точка / как точка, в которой пересе-
каются горизонтали А и А
1
. Точно так же
с помощью плоскости б определена вторая
точка — 2.
Некоторого упрощения можно достичь,
если вспомогательные проецирующие
плоскости проводить через прямые, задаю-
щие плоскость, что и сделано на рис. 88,
где построена линия 1—2 пересечения
плоскостей а (ДЛВС) и р (bbEF). Точка
1 этой линии определена с помощью фрон-
тально проецирующей плоскости у, прове-
денной через сторону DE треугольника
DEF. Именно эта сторона, проекции кото-
рой заданы, и является линией пересече-
38
ния плоскости треугольника DEF и у
(D£ = pflv).
Упрощение графического решения в том
и состоит, что не нужно чертить эту пря-
мую, входящую в число элементов, задаю-
щих плоскость р.
Та же плоскость у пересечет второй тре-
угольник ABC по прямой KL (KL = yПа).
Аналогично, проведя через сторону ВС
горизонтально проецирующую плоскость
б, найдем точку 2. На рис. 88 прямая
ВС =
б|~|а,
а AIjVбf|Э- Пересечение этих
прямых определяет точку 2. Причем ее
фронтальная проекция была построена
раньше, чем 2\.
Внимательный читатель, очевидно, за-
метил, что точки / и 2 являются точками
пересечения сторон одного треугольника
с плоскостью другого.
К детальному рассмотрению этой важ-
ной задачи приступим в § 22.
$ 20. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ
Возможны следующие три случая отно-
сительного расположения прямой и плос-
кости:
прямая принадлежит плоскости;
прямая параллельна плоскости;
прямая пересекает плоскость.
Первому случаю был посвящен § 17,
в котором рассматривалась одна из основ-
ных графических операций — построение
прямых линий, принадлежащих плоскости.
Критерием этого случая является извест-
ное свойство плоскости: если прямая ли-
ния соединяет две точки данной плоскости,
то такая прямая всеми своими точками
лежит в этой плоскости.
Очевидно, что если прямая не имеет
двух общих точек с плоскостью, то она или
параллельна плоскости, или пересекает
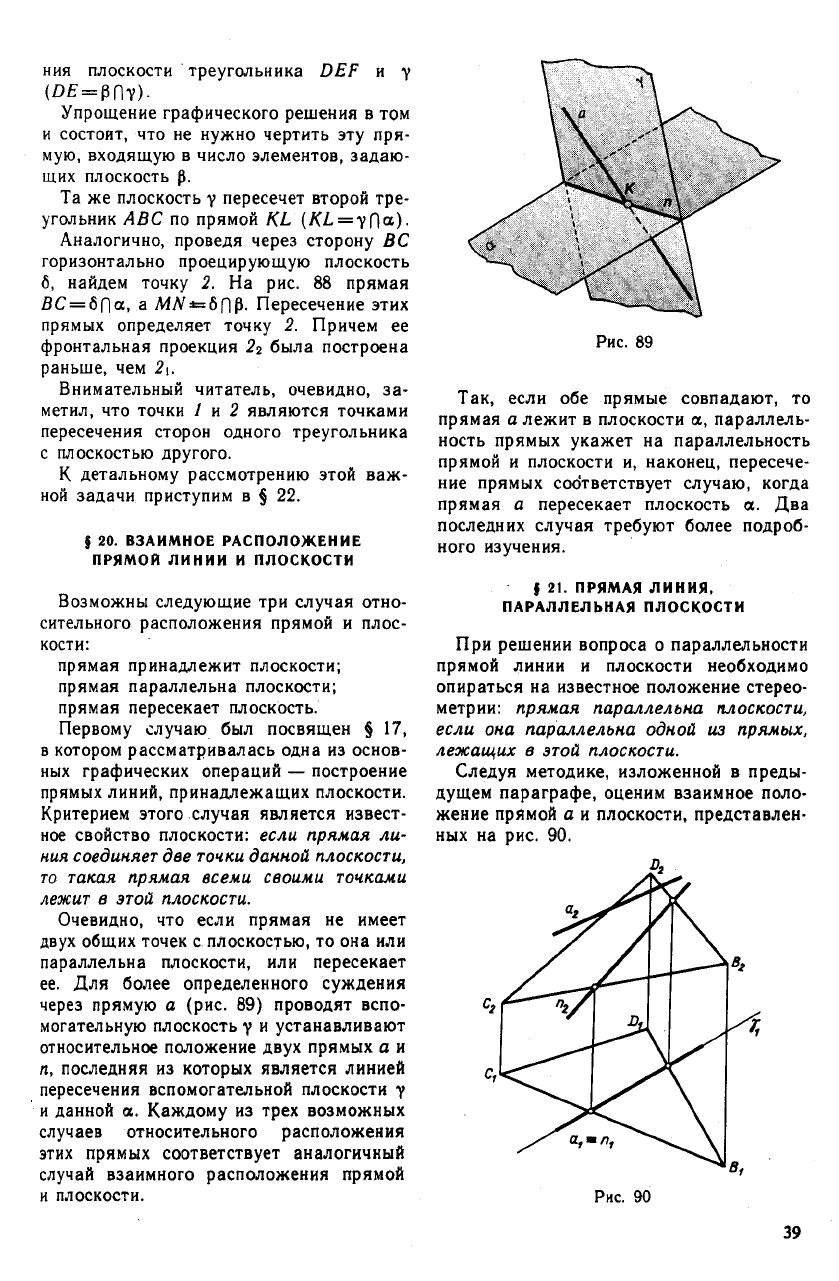
ее. Для более определенного суждения
через прямую а (рис. 89) проводят вспо-
могательную плоскость у и устанавливают
относительное положение двух прямых а и
я, последняя из которых является линией
пересечения вспомогательной плоскости у
и данной а. Каждому из трех возможных
случаев относительного расположения
этих прямых соответствует аналогичный
случай взаимного расположения прямой
и плоскости.
Рис. 89
Так, если обе прямые совпадают, то
прямая а лежит в плоскости а, параллель-
ность прямых укажет на параллельность
прямой и плоскости и, наконец, пересече-
ние прямых соответствует случаю, когда
прямая а пересекает плоскость а. Два
последних случая требуют более подроб-
ного изучения.
| 21. ПРЯМАЯ ЛИНИЯ,
ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
При решении вопроса о параллельности
прямой линии и плоскости необходимо
опираться на известное положение стерео-
метрии: прямая параллельна плоскости,
если она параллельна одной из прямых,
лежащих в этой плоскости.
Следуя методике, изложенной в преды-
дущем параграфе, оценим взаимное поло-
жение прямой а и плоскости, представлен-
39
