Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

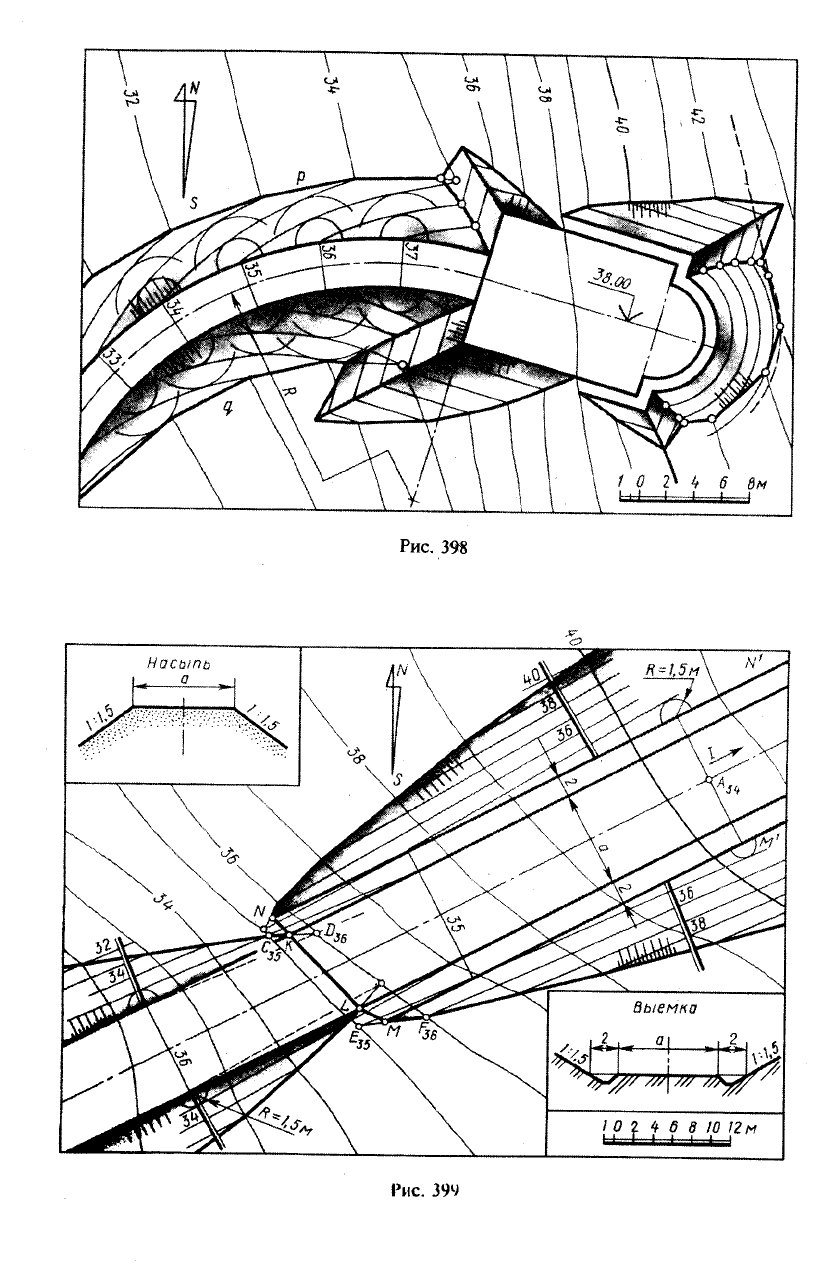
Рис. 398

Рис. 394

полотна до прямых ММ' и A//V' предус-

матривает размещение кюветов (см. про-

филь выемки).

Далее возникает задача на построение

плоскости заданного уклона 1:1,5 и прохо-

дящей через бровку или через прямую,

ограничивающую двухметровый «при-

пуск».

Отметим, что через бровки предстоит

провести откосы насыпи, а через пря-

мые MN

и NN

— откосы выемки.

Решение такой задачи описано в § 78.

Здесь же подчеркнем особенности на-

хождения точек, принадлежащих линии

нулевых работ.

Первые две из них определяются пе-

ресечением границ насыпей с бровками

земляного полотна, вторая пара найдена

пересечением границ выемок с прямы-

ми ММ' и NN'. На рис. 399 штрихами

изображены те горизонтали откосов, с по-

мощью которых построены крайние отрез-

ки ломаных линий пересечения земли и от-

косов.

Эти отрезки и позволяют найти точки

линии нулевых работ. Так, пересечение

бровки и отрезка С35D36 фиксирует точ-

ку К, а ММ

= М.

В заключение заметим, что в практике

проектирования уклоном дорог пренебре-

гают, если /<40

/оо. В этом случае уклон

дороги принимают равным нулю и гори-

зонтали откосов проводят параллельно

бровкам.

Вопросы и задачи для самоконтроля

1. В чем сущность метода проекций с число-

выми отметками и какова область его примене-

ния?

2. Что называют заложением и интервалом

прямой?

3. Проекции прямых а и 6 параллельны, их

уклоны равны. Необходимы или достаточны

приведенные условия для утверждения: a|j6?

4. Что называется масштабом падения плос-

кости?

5. Как построить линию пересечения двух

плоскостей, масштабы падения которых парал-

лельны, но уклоны не равны?

6. Построить план крыши здания, вид сверху

которого имеет П-образную форму, число ска-

тов равно числу сторон заданного контура и все

скаты имеют одинаковый уклон.

7. Что представляет собой поверхность полот-

на дороги на кривой с уклоном?

8. При каком условии бровка полотна дороги

является горизонталью откоса насыпи той же

дороги?

9. Как построить проекции горизонталей по-

верхности одинакового ската?

РАЗДЕЛ 3

ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ,

ПЕРСПЕКТИВЕ И АКСОНОМЕТРИИ

ГЛАВА 15

ГЕОМЕТРИЧЕСКИЕ ОСНОВЫ

ТЕОРИИ ТЕНЕЙ

$ 84. ОБЩИЕ ПОНЯТИЯ

Для того чтобы плоскому чертежу при-

дать большую выразительность, сделать

двумерное изображение наглядным, при-

бегают к построению теней. Особенно ши-

роко используются тени при оформлении

архитектурных проектов (зданий и других

сооружений).

Основная задача теории теней заключа-

ется в определении контуров собствен-

ной и падающей теней данного тела.

Условимся собственными называть тени,

которые получаются на неосвещенной по-

верхности самого тела; тени, отбрасывае-

мые предметом на плоскости проекций,

а также на другие поверхности, будем

именовать падающими.

При построении теней обычно полагают,

что свет распространяется прямолинейно.

Освещение предмета называют ф а-

кельным, если источник света удален

от объекта на незначительное расстояние.

Лучи света при этом образуют связку

прямых.

В том же случае, когда источник света

удален в бесконечность и световые лучи

параллельны друг другу, освещение назы-

вается солнечным.

Чаще всего построение теней осущес-

твляется при параллельных световых лу-

чах. При этом за направление лучей света

обычно принимают направление одной из

диагоналей куба, две грани которого со-

вмещены с плоскостями проекций

(рис. 400 и 401). Проекциями Каждой ди-

агонали такого куба являются соответ-

ствующие диагонали квадратов, т. е. каж-

дая из проекций светового луча составля-

ет с осью х угол 45°.

§ 85. ТЕНЬ ТОЧКИ

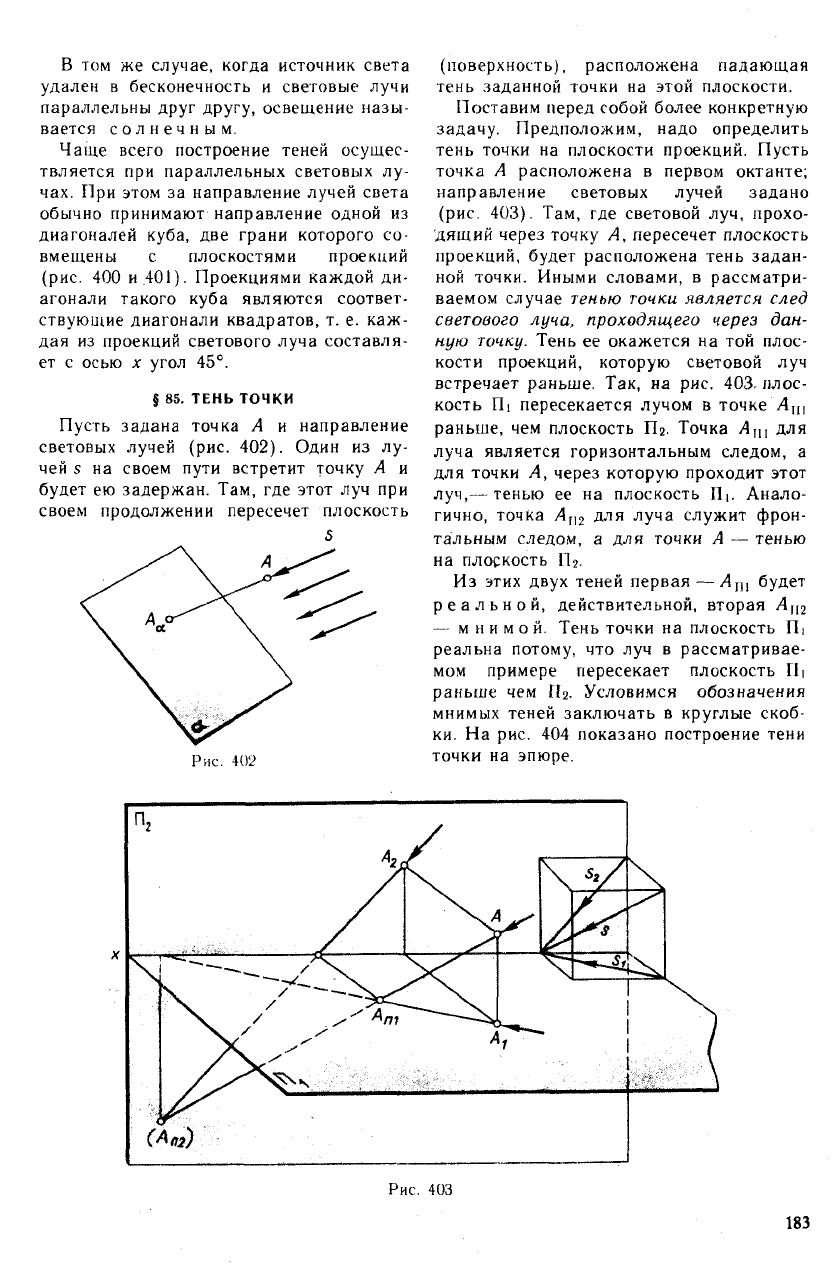
Пусть задана точка А и направление

световых лучей (рис. 402). Один из лу-

чей s на своем пути встретит точку А и

будет ею задержан. Там, где этот луч при

своем продолжении пересечет плоскость

Рис. 402

(поверхность), расположена падающая

тень заданной точки на этой плоскости.

Поставим перед собой более конкретную

задачу. Предположим, надо определить

тень точки на плоскости проекций. Пусть

точка А расположена в первом октанте;

направление световых лучей задано

(рис. 403). Там, где световой луч, прохо-

дящий через точку А, пересечет плоскость

проекций, будет расположена тень задан-

ной точки. Иными словами, в рассматри-

ваемом случае тенью точки является след

светового луча, проходящего через дан-

ную точку. Тень ее окажется на той плос-

кости проекций, которую световой луч

встречает раньше. Так, на рис. 403, плос-

кость П, пересекается лучом в точке А„,

раньше, чем плоскость ГЬ. Точка А

п[

для

луча является горизонтальным следом, а

для точки А, через которую проходит этот

луч,— тенью ее на плоскость П|. Анало-

гично, точка А

и2

ДЛЯ луча служит фрон-

тальным следом, а для точки А — тенью

на плоскость ГЬ.

Из этих двух теней первая — Л

будет

реальной, действительной, вторая Л

п2

— мнимой. Тень точки на плоскость П|

реальна потому, что луч в рассматривае-

мом примере пересекает плоскость П,

раньше чем П

. Условимся обозначения

мнимых теней заключать в круглые скоб-

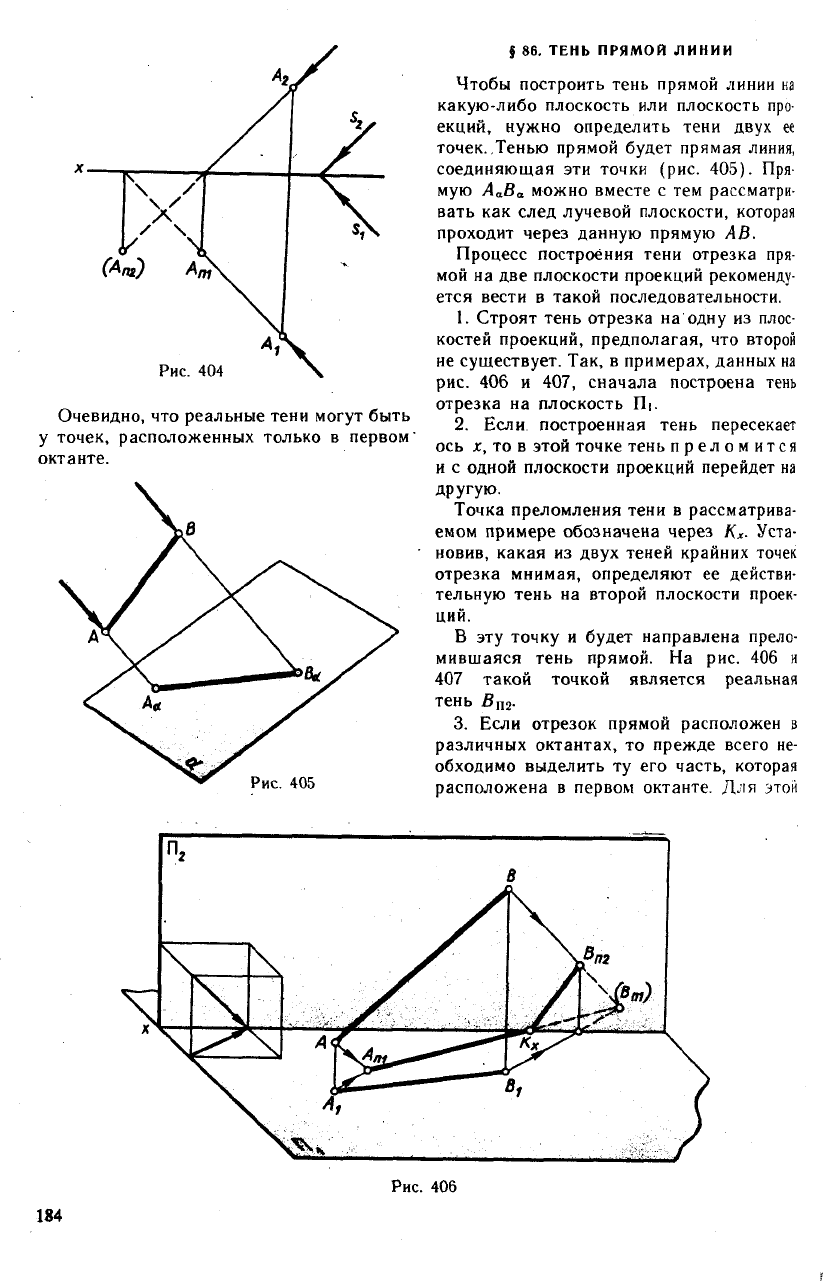
ки. На рис. 404 показано построение тени

точки на эпюре.

183

Очевидно, что реальные тени могут быть

у точек, расположенных только в первом'

октанте.

§ 86. ТЕНЬ ПРЯМОЙ ЛИНИИ

Чтобы построить тень прямой линии на

какую-либо плоскость или плоскость про-

екций, нужно определить тени двух ее

точек. Тенью прямой будет прямая линия,

соединяющая эти точки (рис. 405). Пря-

мую А

можно вместе с тем рассматри-

вать как след лучевой плоскости, которая

проходит через данную прямую АВ.

Процесс построения тени отрезка пря-

мой на две плоскости проекций рекоменду-

ется вести в такой последовательности.

1. Строят тень отрезка на одну из плос-

костей проекций, предполагая, что второй

не существует. Так, в примерах, данных на

рис. 406 и 407, сначала построена тень

отрезка на плоскость П|.

2. Если построенная тень пересекает

ось х, то в этой точке тень преломится

и с одной плоскости проекций перейдет на

другую.

Точка преломления тени в рассматрива-

емом примере обозначена через Кх• Уста-

новив, какая из двух теней крайних точек

отрезка мнимая, определяют ее действи-

тельную тень на второй плоскости проек-

ций.

В эту точку и будет направлена прело-

мившаяся тень прямой. На рис. 406 и

407 такой точкой является реальная

тень В

П2

3. Если отрезок прямой расположен в

различных октантах, то прежде всего не-

обходимо выделить ту его часть, которая

расположена в первом октанте. Для этой

цели приходится определить следы данно-

го отрезка.

Рассмотрим построение тени от прямых

частного положения. Пусть перпендику-

лярная к плоскости П] прямая АВ пе-

ресекает эту плоскость в точке В

(рис. 408, а). В этом случае точ-

ка В совпадает со своей реальной

тенью В

, на плоскости Пь Тенью же

точки А на ту же плоскость П> является

точка А

Соединив эти точки (В

, и

П1

), получим тень прямой АВ на плоско-

сти П|. Она совпадает с горизонтальной

проекцией Светового луча (световые лучи,

проходящие через прямую АВ, образуют

горизонтально проецирующую плоскость,

которая пересекает П, по прямой, совпа-

дающей с горизонтальной проекцией све-

тового луча).

Аналогично строим тень от прямой CD,

перпендикулярной плоскости Пг

(рис. 408,6). Ее тень совпадает с фрон-

тальной проекцией луча.

Нетрудно доказать, что тень от отрез-

ка прямой, параллельного плоскости,

равна и параллельна самому отрезку

§ 87. ТЕНЬ

ПЛОСКОЙ ФИГУРЫ

Пусть дана плоская непрозрачная треу-

гольная пластинка (рис. 409). Для по-

строения ее тени на плоскости а необхо-

димо построить тени всех ее сторон. Тень

периметра треугольника на плоскость ос

будет в общем случае также треугольни-

ком. Вся площадь внутри этого конту-

ра А

— искомая тень пластинки.

Контур этой падающей тени можно рас-

сматривать как сечение лучевой призмы

(ребра которой представляют собой све-

товые лучи, проходящие через верши-

ны заданного треугольника) плос-

костью а.

Построение тени треугольника на две

плоскости проекций необходимо вести в

той же последовательности, что была ре-

комендована для построения тени прямой

(см. § 86). Так, на рис. 410 и 411 прежде

всего построена падающая тень треуголь-

ника на плоскость П

(

в предположении,

что плоскости Пг нет.

Реальной будет та часть тени, которая

расположена на переднем поле плоско-

сти П|. Затем строится тень треугольника

на плоскость П

, для чего в приводимом

примере достаточно определить тень вер-

шины В на плоскость П

. Соединив В

точками преломления теней сторон АВ и

ВС, заканчивают построение.

Исследуя взаимное расположение све-

товых лучей относительно плоскости дан-

ной фигуры, определяют освещенность

проекций этой фигуры. Пример определе-

ния собственной тени треугольника ABC

О б) 6)

шй

»В

П1

ис

. 408

186

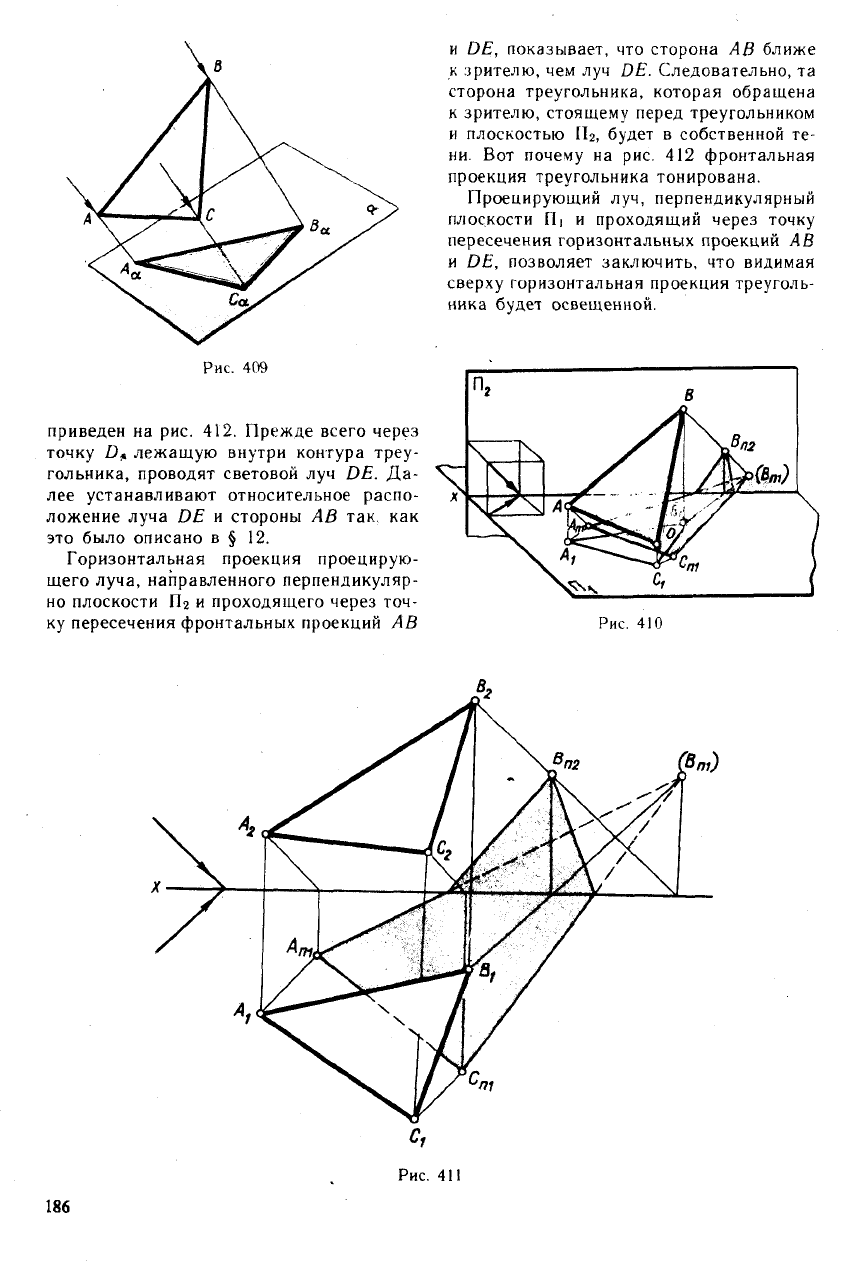
Рис. 409

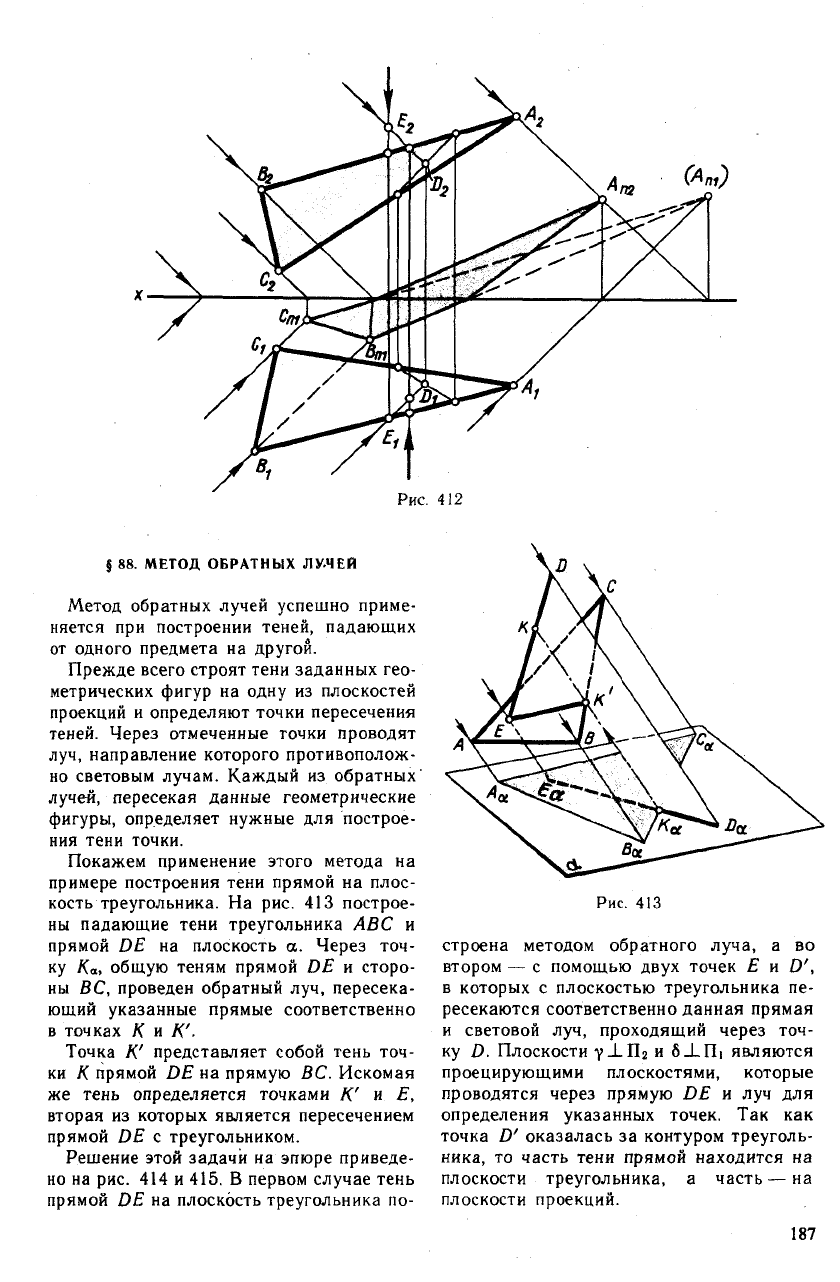
приведен на рис. 412. Прежде всего через

точку D, лежащую внутри контура треу-

гольника, проводят световой луч DE. Да-

лее устанавливают относительное распо-

ложение луча DE и стороны АВ так как

это было описано в § 12.

Горизонтальная проекция проецирую-

щего луча, направленного перпендикуляр-

но плоскости Пг и проходящего через точ-

ку пересечения фронтальных проекций АВ

и DE, показывает, что сторона АВ ближе

к зрителю, чем луч DE. Следовательно, та

сторона треугольника, которая обращена

к зрителю, стоящему перед треугольником

и плоскостью П

, будет в собственной те-

ни. Вот почему на рис. 412 фронтальная

проекция треугольника тонирована.

Проецирующий луч, перпендикулярный

плоскости Г1| и проходящий через точку

пересечения горизонтальных проекций АВ

и DE, позволяет заключить, что видимая

сверху горизонтальная проекция треуголь-

ника будет освещенной.

Рис. 410

186

§ 88. МЕТОД ОБРАТНЫХ ЛУЧЕЙ

Метод обратных лучей успешно приме-

няется при построении теней, падающих

от одного предмета на другой.

Прежде всего строят тени заданных гео-

метрических фигур на одну из плоскостей

проекций и определяют точки пересечения

теней. Через отмеченные точки проводят

луч, направление которого противополож-

но световым лучам. Каждый из обратных

лучей, пересекая данные геометрические

фигуры, определяет нужные для построе-

ния тени точки.

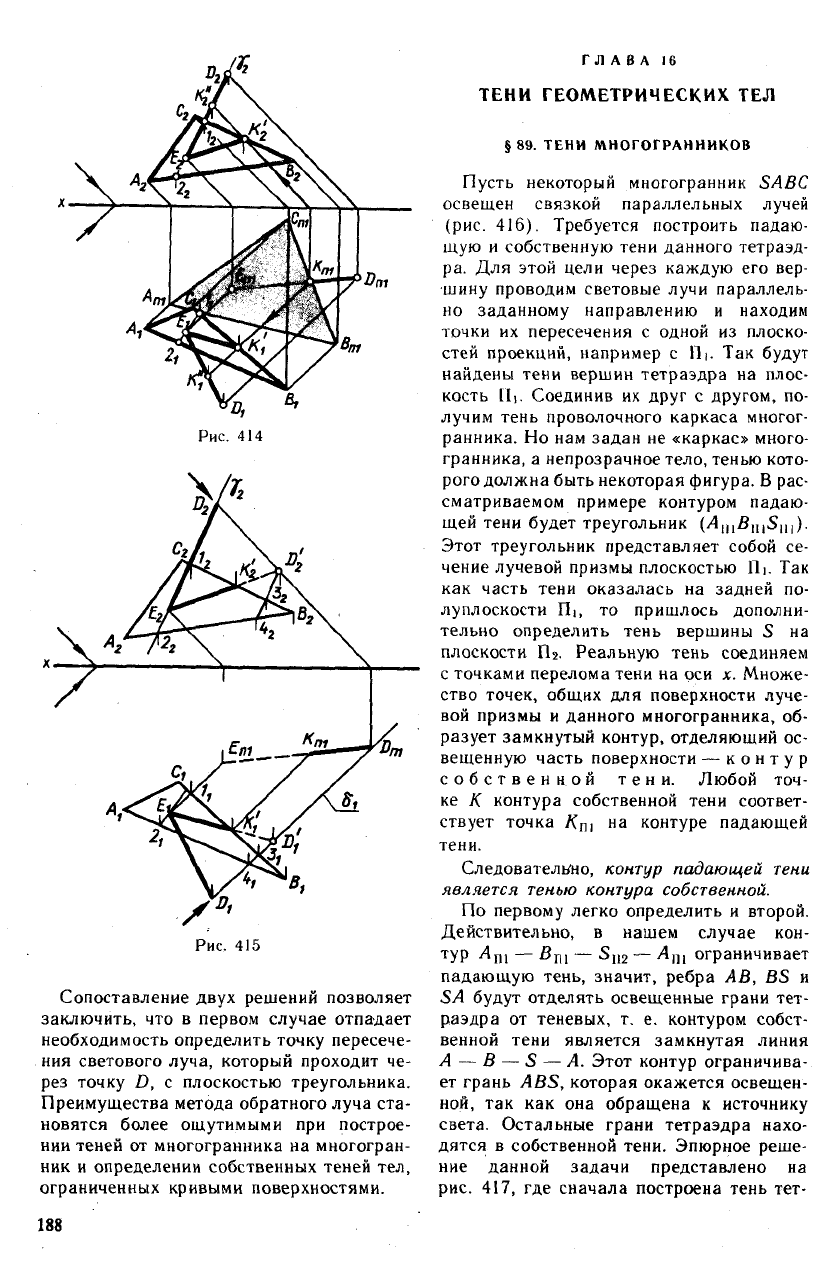
Покажем применение этого метода на

примере построения тени прямой на плос-

кость треугольника. На рис. 413 построе-

ны падающие тени треугольника ABC и

прямой DE на плоскость а. Через точ-

ку Ка, общую теням прямой DE и сторо-

ны ВС, проведен обратный луч, пересека-

ющий указанные прямые соответственно

в точках К и К'-

Точка К' представляет собой тень точ-

ки К прямой DE на прямую ВС. Искомая

же тень определяется точками К' и Е,

вторая из которых является пересечением

прямой DE с треугольником.

Решение этой задачи на эпюре приведе-

но на рис. 414 и 415. В первом случае тень

прямой DE на плоскость треугольника по-

строена методом обратного луча, а во

втором — с помощью двух точек Е и D',

в которых с плоскостью треугольника пе-

ресекаются соответственно данная прямая

и световой луч, проходящий через точ-

ку D. Плоскости v J-Пг и б_LП| являются

проецирующими плоскостями, которые

проводятся через прямую DE и луч для

определения указанных точек. Так как

точка D' оказалась за контуром треуголь-

ника, то часть тени прямой находится на

плоскости треугольника, а часть — на

плоскости проекций.

187

Сопоставление двух решений позволяет

заключить, что в первом случае отпадает

необходимость определить точку пересече-

ния светового луча, который проходит че-

рез точку D, с плоскостью треугольника.

Преимущества метода обратного луча ста-

новятся более ощутимыми при построе-

нии теней от многогранника на многогран-

ник и определении собственных теней тел,

ограниченных кривыми поверхностями.

ГЛАВА 16

ТЕНИ ГЕОМЕТРИЧЕСКИХ ТЕЛ

§89. ТЕНИ МНОГОГРАННИКОВ

Пусть некоторый многогранник SABC

освещен связкой параллельных лучей

(рис. 416). Требуется построить падаю-

щую и собственную тени данного тетраэд-

ра. Для этой цели через каждую его вер-

шину проводим световые лучи параллель-

но заданному направлению и находим

точки их пересечения с одной из плоско-

стей проекций, например с П|. Так будут

найдены тени вершин тетраэдра на плос-

кость II). Соединив их друг с другом, по-

лучим тень проволочного каркаса многог-

ранника. Но нам задан не «каркас» много-

гранника, а непрозрачное тело, тенью кото-

рого должна быть некоторая фигура. В рас-

сматриваемом примере контуром падаю-

щей тени будет треугольник (ЛщБц^щ).

Этот треугольник представляет собой се-

чение лучевой призмы плоскостью Hi. Так

как часть тени оказалась на задней по-

луплоскости П|, то пришлось дополни-

тельно определить тень вершины S на

плоскости Пг. Реальную тень соединяем

с точками перелома тени на оси х. Множе-

ство точек, общих для поверхности луче-

вой призмы и данного многогранника, об-

разует замкнутый контур, отделяющий ос-

вещенную часть поверхности — контур

собственной тени. Любой точ-

ке К контура собственной тени соответ-

ствует точка К

на контуре падающей

тени.

Следовательно, контур падающей тени

является тенью контура собственной.

По первому легко определить и второй.

Действительно, в нашем случае кон-

тур А

— В

— S

1(2

— А

ограничивает

падающую тень, значит, ребра АВ, BS и

SA будут отделять освещенные грани тет-

раэдра от теневых, т. е. контуром собст-

венной тени является замкнутая линия

А — В — S — А. Этот контур ограничива-

ет грань ABS, которая окажется освещен-

ной, так как она обращена к источнику

света. Остальные грани тетраэдра нахо-

дятся в собственной тени. Эпюрное реше-

ние данной задачи представлено на

рис. 417, где сначала построена тень тет-

188

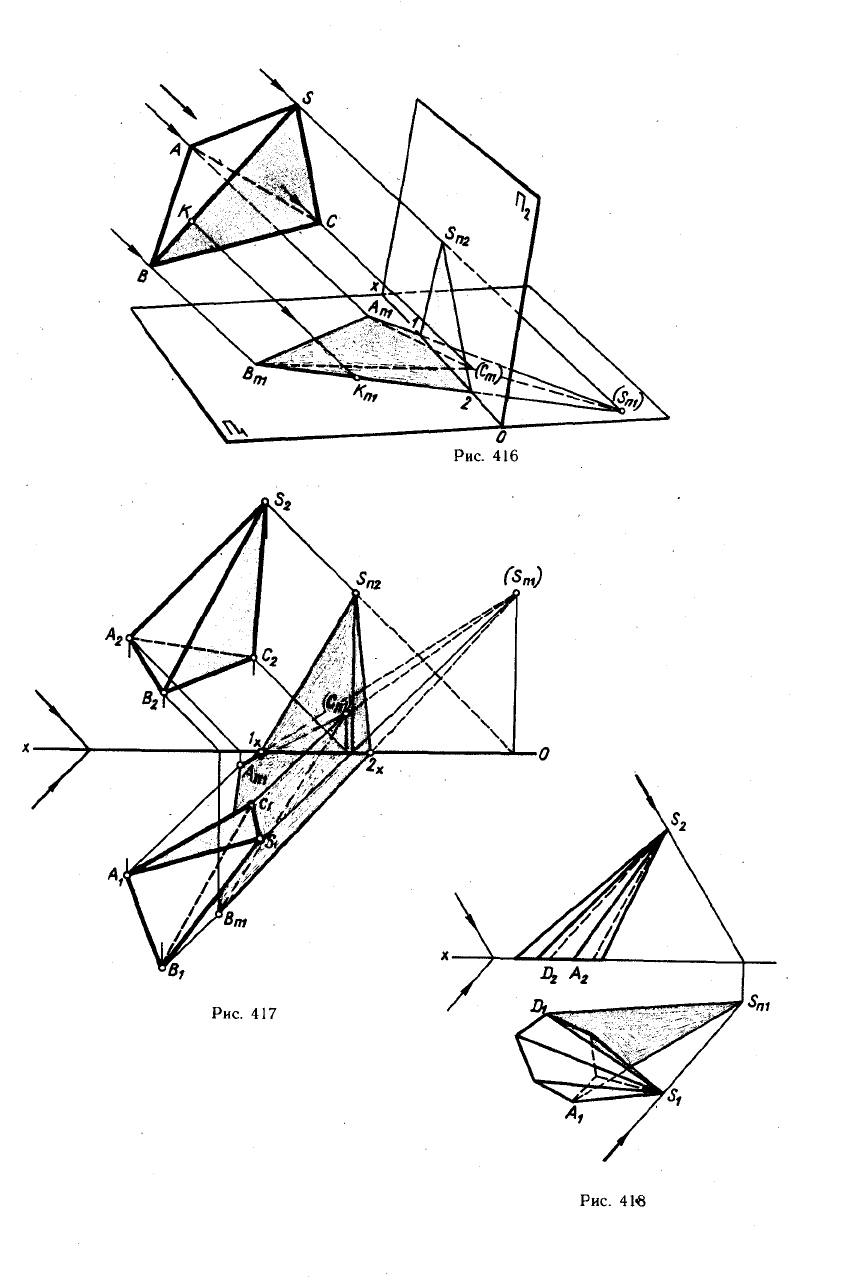
Рис. 41-8