Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

раэдра на FIi, а затем с помощью реальной

тени 5л2 найден контур падающей тени

на П2.

Построение теней упрощается, если ос-

нование многогранника расположено на

плоскости проекций. В этом случае все

вершины основания совмещены со своими

тенями. Для построения тени пирамиды

(рис. 418) достаточно найти тень ее вер-

шины и полученную точку S

соединить

с крайними точками основания.

Грани пирамиды, к которым примыкает

падающая тень, окажутся в тени собствен-

ной.

§90. ТЕНИ ПЕРЕСЕКАЮЩИХСЯ

МНОГОГРАННИКОВ

Задача построения теней пересекаю-

щихся многогранников не ограничивается

определением контуров собственных теней

и падающих на плоскости проекций. Реше-

ние задачи завершается построением па-

дающих теней от неосвещенных граней

одного тела на пересекающиеся с ними

освещенные грани второго.

Линии искомого контура представляют

собой пересечение лучевых плоскостей,

проходящих через контур собственной те-

ни одного многогранника, с освещенными

гранями второго. Таким образом, основой

всех построений является определение те-

ни прямой на плоскость. Такая задача

рассматривалась в § 88, где для ее реше-

ния был использован метод обратных лу-

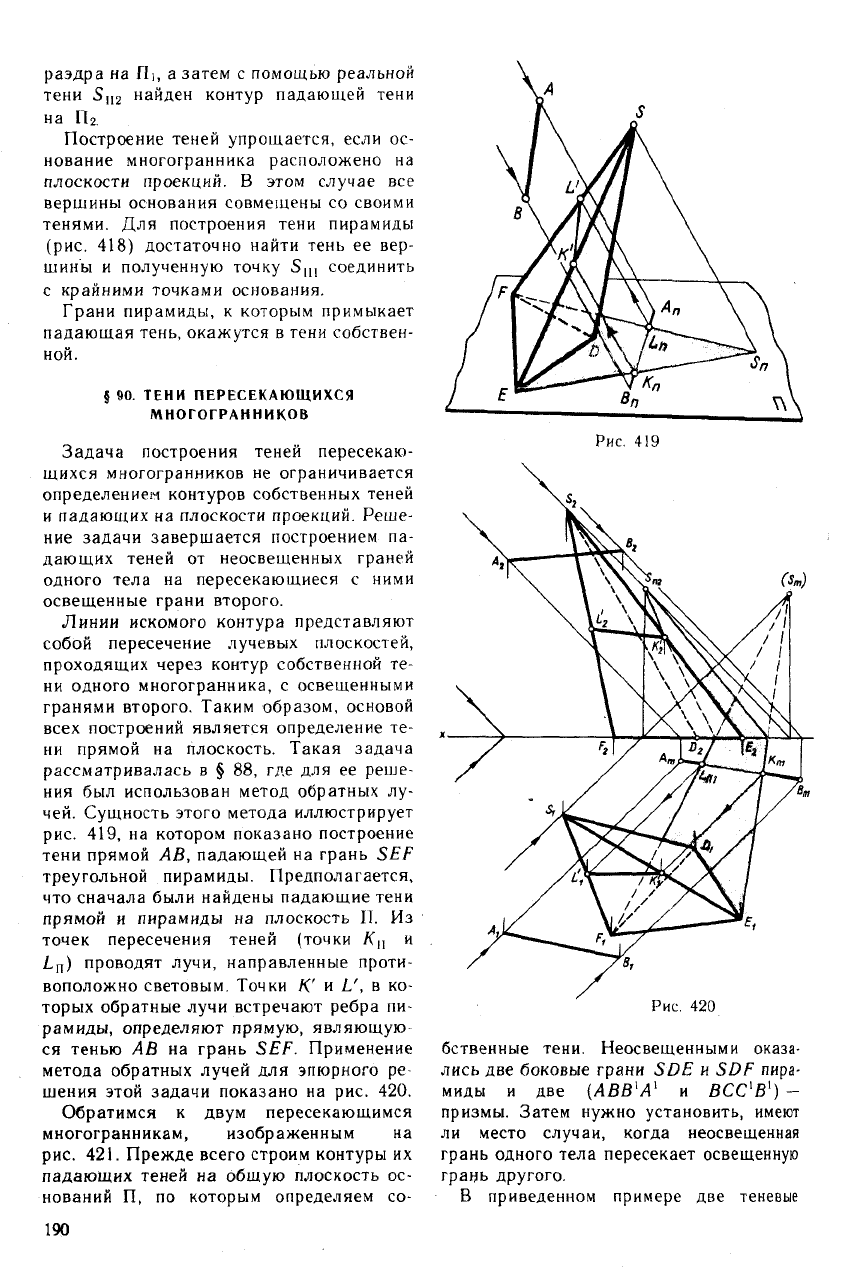
чей. Сущность этого метода иллюстрирует

рис. 419, на котором показано построение

тени прямой АВ, падающей на грань SEF

треугольной пирамиды. Предполагается,

что сначала были найдены падающие тени

прямой и пирамиды на плоскость II. Из

точек пересечения теней (точки /С

) проводят лучи, направленные проти-

воположно световым. Точки К' и L', в ко-

торых обратные лучи встречают ребра пи-

рамиды, определяют прямую, являющую-

ся тенью АВ на грань SEF. Применение

метода обратных лучей для эпюрного ре

шения этой задачи показано на рис. 420.

Обратимся к двум пересекающимся

многогранникам, изображенным на

рис. 421. Прежде всего строим контуры их

падающих теней на общую плоскость ос-

нований П, по которым определяем со-

бственные тени. Неосвещенными оказа-

лись две боковые грани SDE и SDF пира-

миды и две (АВВ

[

и ВСС'В

) -

призмы. Затем нужно установить, имеют

ли место случаи, когда неосвещенная

грань одного тела пересекает освещенную

грань другого.

В приведенном примере две теневые

190

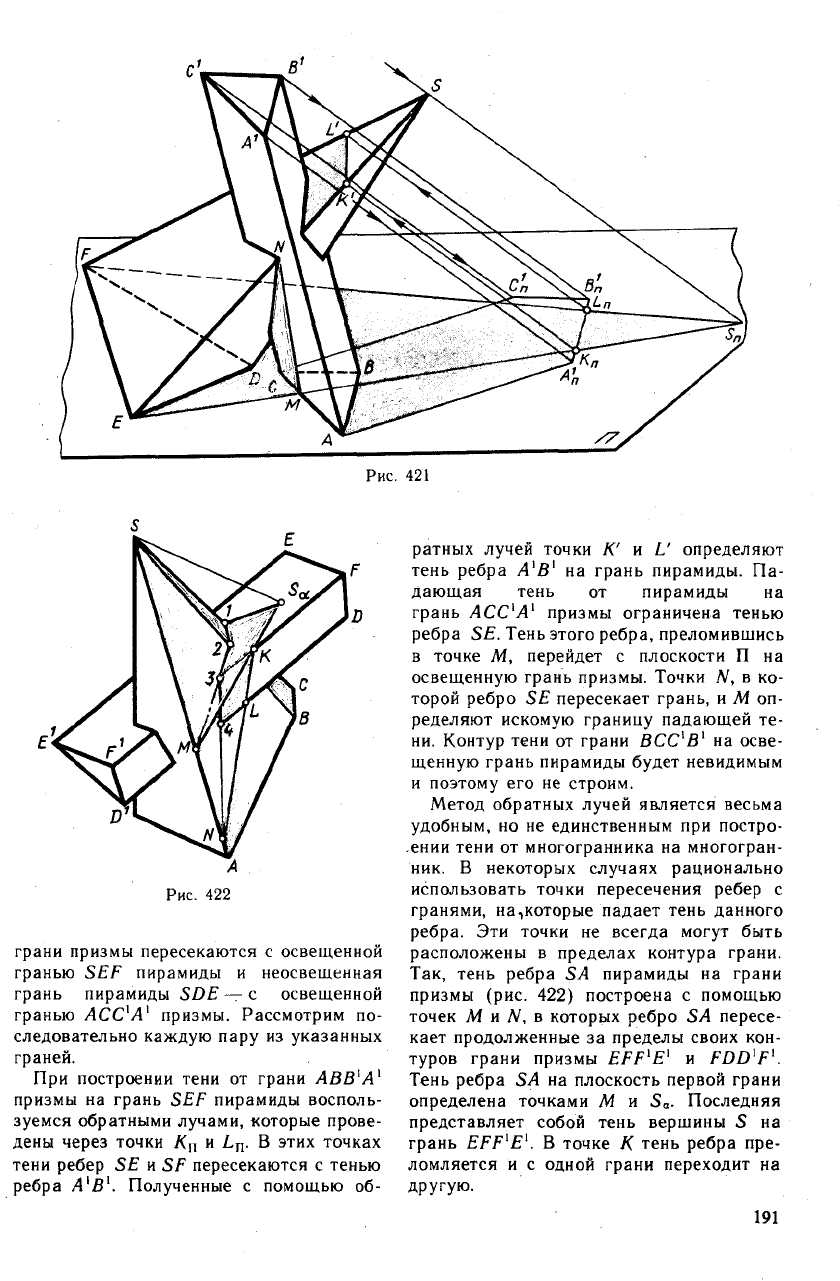
Рис. 421

грани призмы пересекаются с освещенной

гранью SEF пирамиды и неосвещенная

грань пирамиды SDE — с освещенной

гранью АСС'А' призмы. Рассмотрим по-

следовательно каждую пару из указанных

граней.

При построении тени от грани ABB'А

призмы на грань SEF пирамиды восполь-

зуемся обратными лучами, которые прове-

дены через точки Кц

^-п- В этих точках

тени ребер SE и SF пересекаются с тенью

ребра А'В

. Полученные с помощью об-

ратных лучей точки К' и L' определяют

тень ребра А'В

на грань пирамиды. Па-

дающая тень от пирамиды на

грань АСС'А

призмы ограничена тенью

ребра SE. Тень этого ребра, преломившись

в точке М, перейдет с плоскости П на

освещенную грань призмы. Точки N, в ко-

торой ребро SE пересекает грань, и М оп-

ределяют искомую границу падающей те-

ни. Контур тени от грани ВСС'В' на осве-

щенную грань пирамиды будет невидимым

и поэтому его не строим.

Метод обратных лучей является весьма

удобным, но не единственным при постро-

ении тени от многогранника на многогран-

ник. В некоторых случаях рационально

использовать точки пересечения ребер с

гранями, на

которые падает тень данного

ребра. Эти точки не всегда могут быть

расположены в пределах контура грани.

Так, тень ребра Sv4 пирамиды на грани

призмы (рис. 422) построена с помощью

точек М и N, в которых ребро SA пересе-

кает продолженные за пределы своих кон-

туров грани призмы EFF'E' и FDD'F'.

Тень ребра S.4 на плоскость первой грани

определена точками М и S„. Последняя

представляет собой тень вершины S на

грань EFF'E

. В точке К тень ребра пре-

ломляется и с одной грани переходит на

другую.

191

§ 91. ТЕНИ ТЕЛ, ОГРАНИЧЕННЫХ

КРИВЫМИ ПОВЕРХНОСТЯМИ

Световые лучи, касаясь тела произволь-

ной формы, в общем случае образуют ц и-

линдрическую поверхность, а не

призму, как это было у многогранников

Линия касания лучевого цилиндра и дан-

ного тела отделяет освещенную часть его

от неосвещенной. Это контур собственной

тени. Линия пересечения лучевой цилин-

дрической поверхности с плоскостью про-

екций или другой поверхностью служит

контуром падающей тени. Как и прежде,

контур падающей тени является тенью от

контура собственной.

В одних случаях каждый контур можно

строить независимо один от другого, в

других сначала целесообразно определять

контур собственной тени и по нему нахо-

дить падающую, в третьих — наоборот.

Приводимые ниже примеры поясняют ска-

занное.

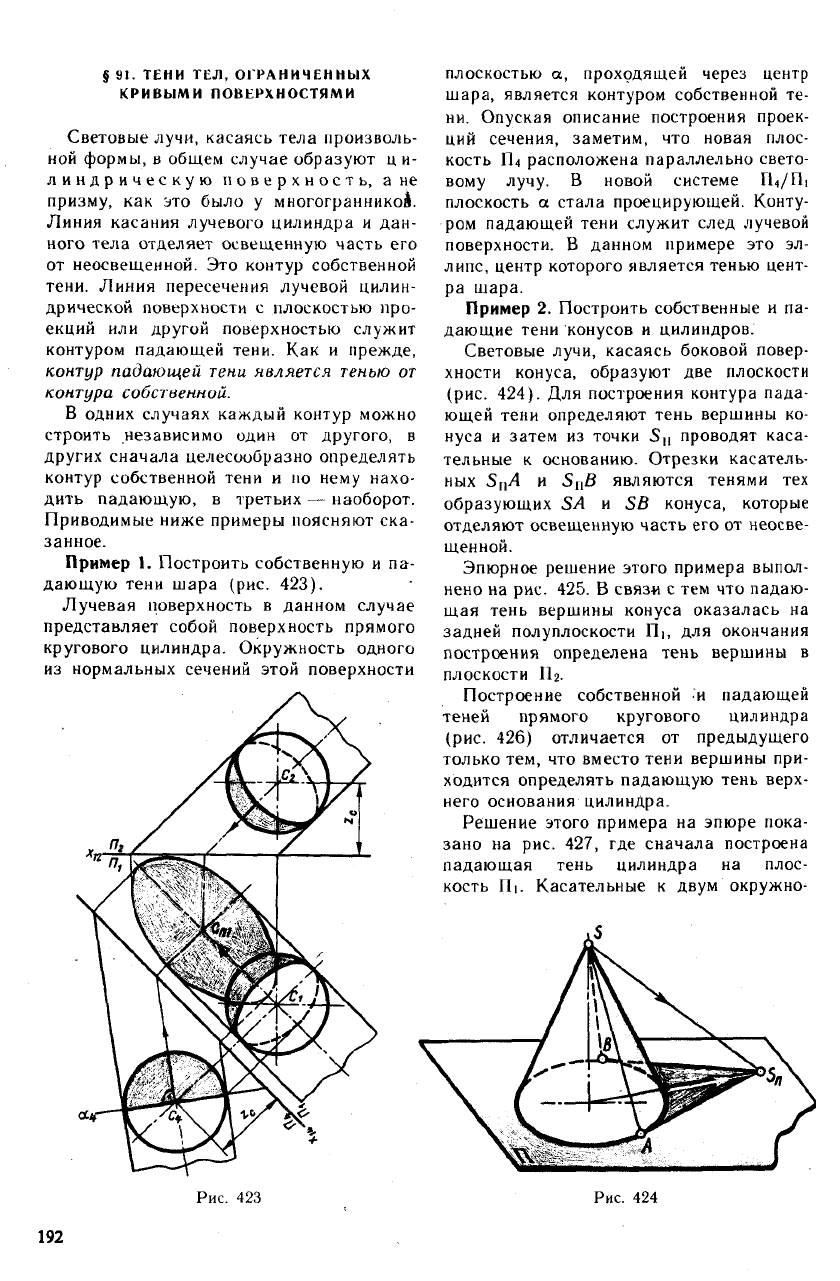
Пример 1. Построить собственную и па-

дающую тени шара (рис. 423).

Лучевая поверхность в данном случае

представляет собой поверхность прямого

кругового цилиндра. Окружность одного

из нормальных сечений этой поверхности

плоскостью а, проходящей через центр

шара, является контуром собственной те-

ни. Опуская описание построения проек-

ций сечения, заметим, что новая плос-

кость Ш расположена параллельно свето-

вому лучу. В новой системе Г1

П i

плоскость а стала проецирующей. Конту-

ром падающей тени служит след лучевой

поверхности. В данном примере это эл-

липс, центр которого является тенью цент-

ра шара.

Пример 2. Построить собственные и па-

дающие тени конусов и цилиндров.

Световые лучи, касаясь боковой повер-

хности конуса, образуют две плоскости

(рис. 424). Для построения контура пада-

ющей тени определяют тень вершины ко-

нуса и затем из точки S|

проводят каса-

тельные к основанию. Отрезки касатель-

ных 5

Л и 5

В являются тенями тех

образующих S/1 и SB конуса, которые

отделяют освещенную часть его от неосве-

щенной.

Эпюрное решение этого примера выпол-

нено на рис. 425. В связи с тем что падаю-

щая тень вершины конуса оказалась на

задней полуплоскости Пь для окончания

построения определена тень вершины в

плоскости Иг-

Построение собственной и падающей

теней прямого кругового цилиндра

(рис. 426) отличается от предыдущего

только тем, что вместо тени вершины при-

ходится определять падающую тень верх-

него основания цилиндра.

Решение этого примера на эпюре пока-

зано на рис. 427, где сначала построена

падающая тень цилиндра на плос-

кость Пь Касательные к двум окружно-

Рис. 423 Рис. 424

192

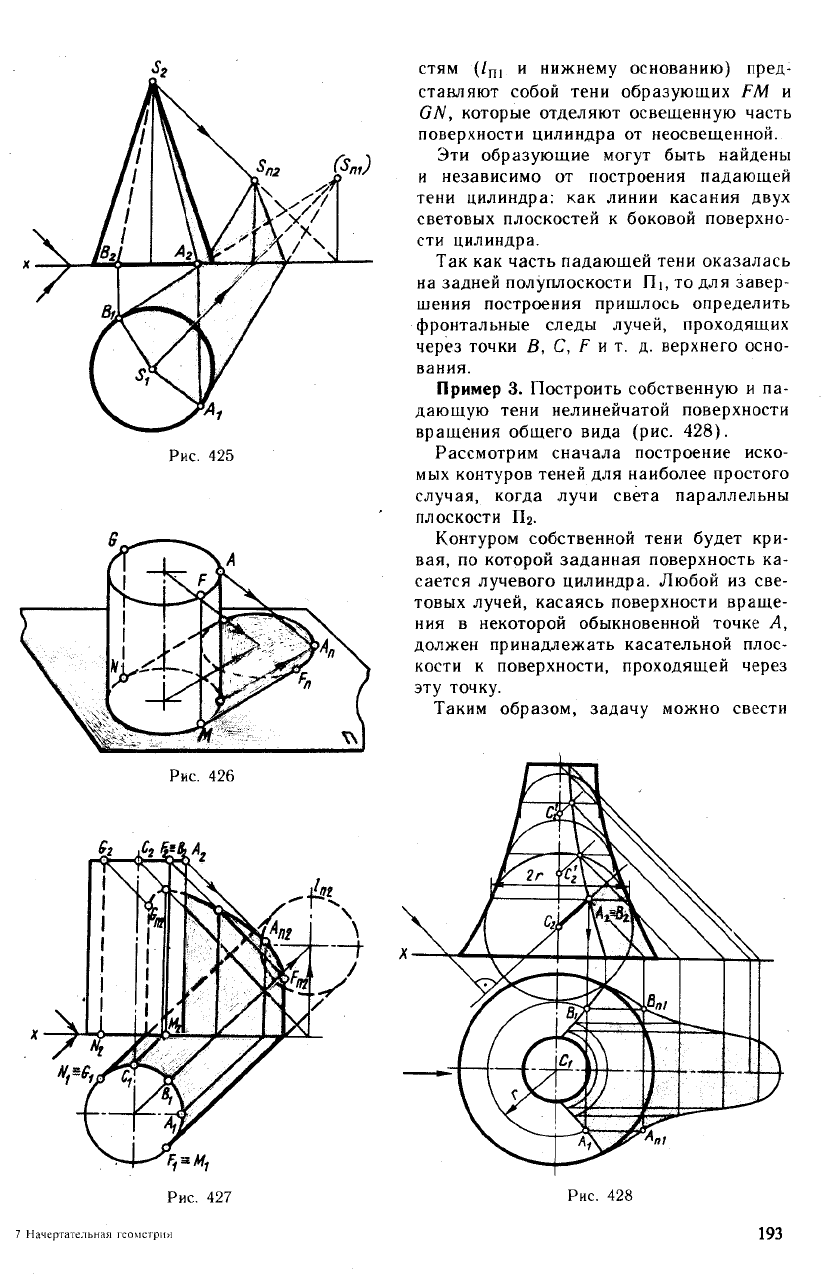
стям (/

п|

и нижнему основанию) пред-

ставляют собой тени образующих FM и

GN, которые отделяют освещенную часть

поверхности цилиндра от неосвещенной.

Эти образующие могут быть найдены

и независимо от построения падающей

тени цилиндра: как линии касания двух

световых плоскостей к боковой поверхно-

сти цилиндра.

Так как часть падающей тени оказалась

на задней полуплоскости 111, то для завер-

шения построения пришлось определить

фронтальные следы лучей, проходящих

через точки В, С, F и т. д. верхнего осно-

вания.

Пример 3. Построить собственную и па-

дающую тени нелинейчатой поверхности

вращения общего вида (рис. 428).

Рассмотрим сначала построение иско-

мых контуров теней для наиболее простого

случая, когда лучи света параллельны

плоскости Пг.

Контуром собственной тени будет кри-

вая, по которой заданная поверхность ка-

сается лучевого цилиндра. Любой из све-

товых лучей, касаясь поверхности враще-

ния в некоторой обыкновенной точке А,

должен принадлежать касательной плос-

кости к поверхности, проходящей через

эту точку.

Таким образом, задачу можно свести

7 Начертательная геометрия

193

Рис. 429

к определению множества то-

чек, в которых плоскости, па-

раллельные световому лучу, ка-

саются данной поверхности.

Для решения так сформулированной за-

дачи в поверхность вращения вписывают

сферы и строят проекции тех окружностей,

по которым каждая сфера касается дан-

ной поверхности. Так, сфера с центром

в точке С касается поверхности вращения

по окружности радиуса г. Радиус вспомо-

гательной сферы, проведенный в искомую

точку касания, должен быть нормалью

к касательной плоскости. Значит, фрон-

тальная проекция радиуса С

должна

составлять прямой угол с одноименной

проекцией фронтали касательной плоско-

сти. В приведенном примере касательная

плоскость должна быть параллельна

фронтально расположенным световым лу-

чам. Вот почему прямая С

перпендику-

лярна фронтальной проекции луча

(см. рис. 428). Точка А, в которой радиус

пересекает окружность касания сферы и

поверхности вращения, принадлежит ис-

комому контуру собственной тени. Гори-

зонтальная проекция точки А (и ей сим-

метричной В) определяется как точка пе-

ресечения горизонтальной проекции па-

раллели радиуса г и линии проекционной

связи. Аналогично находят и остальные

точки. Контур падающей тени строят как

тень от контура собственной.

Дополнительные построения, которые

приходится выполнять, если световые лучи

не параллельны плоскостям проекций, по-

казаны на рис. 429. Здесь прежде всего

построены новые проекции (s| и si) свето-

вого луча, повернутого на угол ф до поло-

жения, параллельного 1Ь. Затем, соглас-

но изложенной выше методике, найдена

проекция точки А\ принадлежащей кон-

туру собственной тени. Остается проде-

лать обратное преобразование эпюра, за-

ключающееся в повороте найденных точек

вокруг оси поверхности вращения на

угол ф против движения часовой стрелки.

§ 92. ТЕНИ НА ФАСАДАХ ЗДАНИЙ

Построение теней на фасадах зданий

основано на определении точек пересече-

ния световых лучей с вертикальными плос-

костями фасада или с наклонными ската-

ми крыши. Кроме фасада зданйя, для

выполнения построений необходимо иметь

заданной еще одну проекцию (план или

боковой фасад).

Определяя контур падающей тени, кото-

рый является параллельной проекцией

контура собственной тени, рекомендуется

пользоваться следующими правилами.

1. Тень от плоской фигуры, падающая

на параллельную ей плоскость, равна са-

мой фигуре,

так

как линии сечения лучево-

го цилиндра (призмы) параллельными

плоскостями всегда конгруэнтны. В час-

тности, тень отрезка прямой на параллель-

ную ему плоскость равна и параллельна

самому отрезку (см. рис. 408).

2. Если прямая перпендикулярна неко-

торой плоскости а, то тень прямой на

плоскости а совпадает с направлением

проекции луча на

ту

же плоскость. Объяс-

няется это, как было показано в § 86, тем,

что световые лучи в данном случае обра-

зуют плоскость, которая по отношению

к а является проецирующей.

Покажем применение указанных правил

для построения теней на фасаде здания,

ортогональные проекции (фасад и план)

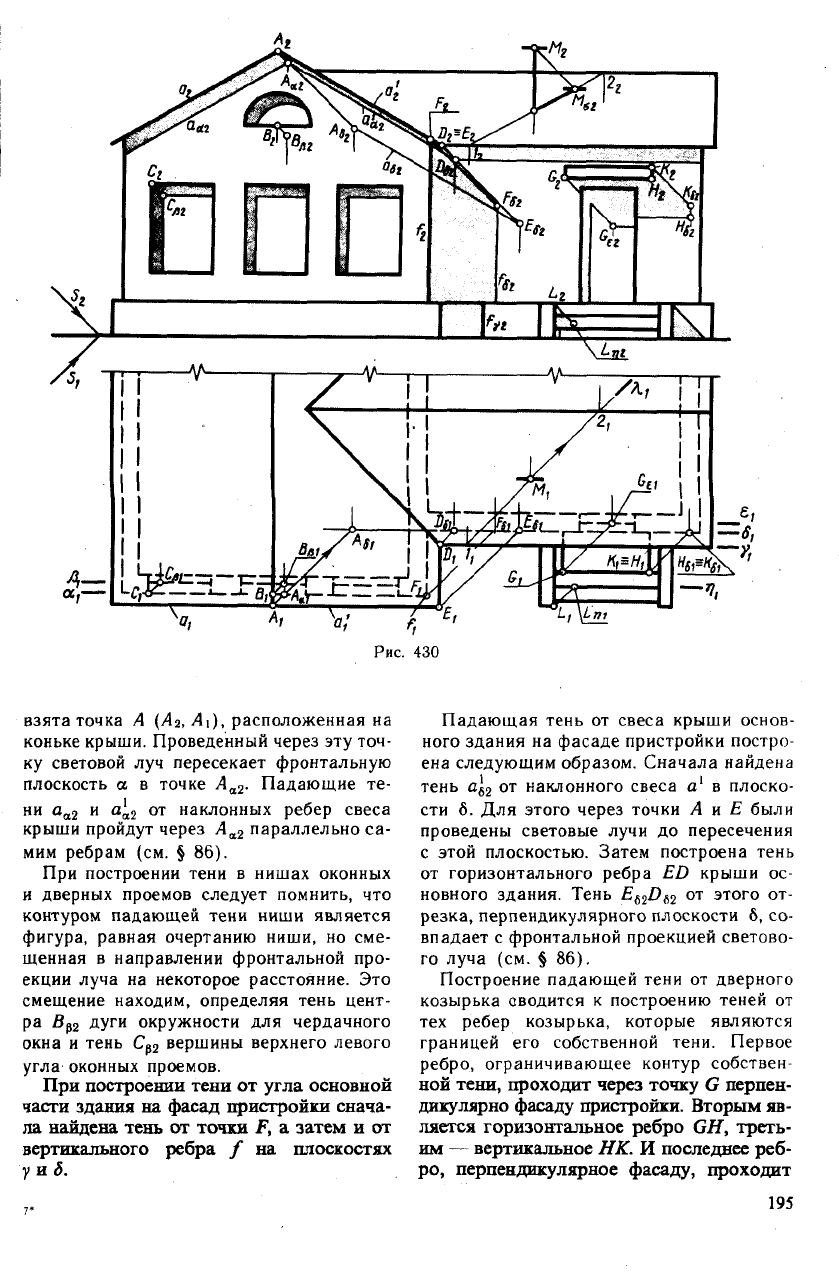
которого показаны на рис. 430. Там же

прямой s задано направление светового

луча.

Для построения тени от фронтального

свеса крыши, ограниченного спереди ли-

нией а, достаточно найти тень от произ-

вольной точки, принадлежащей этой ли-

нии. На рис. 430 в качестве такой точки

194

.JZZZZZTFY ,

ТТ/ TT

Рис. 430

взята точка А (Л

, Л1), расположенная на

коньке крыши. Проведенный через эту точ-

ку световой луч пересекает фронтальную

плоскость а в точке Л

о2

. Падающие те-

ни а

а2

и а'

от наклонных ребер свеса

крыши пройдут через Л

а2

параллельно са-

мим ребрам (см. § 86).

При построении тени в нишах оконных

и дверных проемов следует помнить, что

контуром падающей тени ниши является

фигура, равная очертанию ниши, но сме-

щенная в направлении фронтальной про-

екции луча на некоторое расстояние. Это

смещение находим, определяя тень цент-

ра Вр

дуги окружности для чердачного

окна и тень С

р2

вершины верхнего левого

угла оконных проемов.

При построении тени от угла основной

части здания на фасад пристройки снача-

ла найдена тень от точки F, а затем и от

вертикального ребра / на плоскостях

у и 5.

Падающая тень от свеса крыши основ-

ного здания на фасаде пристройки постро-

ена следующим образом. Сначала найдена

тень al

от наклонного свеса а

[

в плоско-

сти б. Для этого через точки Д и £ были

проведены световые лучи до пересечения

с этой плоскостью. Затем построена тень

от горизонтального ребра ED крыши ос-

новного здания. Тень E

Df,

от этого от-

резка, перпендикулярного плоскости 6, со-

впадает с фронтальной проекцией светово-

го луча (см. § 86).

Построение падающей тени от дверного

козырька сводится к построению теней от

тех ребер козырька, которые являются

границей его собственной тени. Первое

ребро, ограничивающее контур собствен-

ной тени, проходит через точку G перпен-

дикулярно фасаду пристройки. Вторым яв-

ляется горизонтальное ребро GH, треть-

им — вертикальное НК. И последнее реб-

ро, перпендикулярное фасаду, проходит

195

Рис. 431

через точку К. Для построения тени от

козырька были найдены тени от вершин

этой ломаной линии: точек G, Н и К в

плоскостях б и е.

Тень L

от верхней точки L ребра ог-

раждения, как видно из чертежа, падает

на вертикальную плоскость подступенка

лестницы. Поэтому с правой стороны па-

дающая тень от ограждения лестницы ог-

раничена двумя вертикальными отрезками

и наклонным под углом 45° отрезком,

представляющим собой тень от горизон-

тального ребра ограждения, перпендику-

лярного фасаду здания.

И наконец, для построения тени от ан-

тенны на плоскость крыши а найдена точ-

ка пересечения светового луча, проходя-

щего через вершину М антенны. Для это-

го световой луч был предварительно

заключен в горизонтально проецирующую

плоскость X, которая пересекла плоскость

крыши по линии 1—2. В месте пересече-

ния фронтальной проекции луча с фрон-

тальной проекцией линии 1—2 определена

точка М

а2

В заключение рассмотрим пример опре-

деления тени от трубы на плоскость кры-

ши (рис. 431). Опуская описание построе-

ний, связанных с нахождением точек пе-

ресечения световых лучей с профильно

проецирующей плоскостью ската крыши,

докажем, что тень от вертикальных ребер

трубы на наклонную плоскость крыши

проецируется на Пг в прямую, составляю-

щую с осью х тот же угол q>, который

образует с плоскостью Г11 данный скат

крыши.

Действительно, из равенства треугольни-

ков А

а2

и АзВзА^з (они равны по двум

сторонам и углу, заключенному между

ними) следует, что АА

а2

— ААзВзА

з,

а значит, и /L(pi=Z_<p как доцолняющие

равные углы до 90°.

ГЛАВА 17

ТЕНИ В ПЕРСПЕКТИВЕ

И АКСОНОМЕТРИИ

Для придания перспективным и аксоно-

метрическим проекциям большей вырази-

тельности строят собственные и падающие

тени изображенных предметов. В основу

этих построений положены те же предпо-

сылки, которые были рассмотрены в гла-

вах 15 и 16, посвященных геометрической

теории теней и ее приложениям в ортого-

нальных проекциях.

Не повторяя их заново, перейдем к кон-

кретным примерам построения теней в

перспективе и аксонометрии, на которых

покажем некоторые особенности, прису-

щие этим методам.

С целью упрощения (в разделе теней)

перспективы точек и их вторичные проек-

ции обозначаются прописными буквами

(или цифрами), но без правого верхнего

штриха. Например, А и A

вместо А' и А\.

$ 93. ТЕНИ В ЛИНЕЙНОЙ ПЕРСПЕКТИВЕ

Так как источник света считается

удаленным в бесконечность, то вторичная

проекция его должна быть на линии гори-

зонта. Что касается перспективы источни-

ка света (Солнца), то она может быть как

под линией горизонта, так и над ней, при-

чем в обоих случаях само Солнце располо-

жено над плоскостью горизонта Г.

196

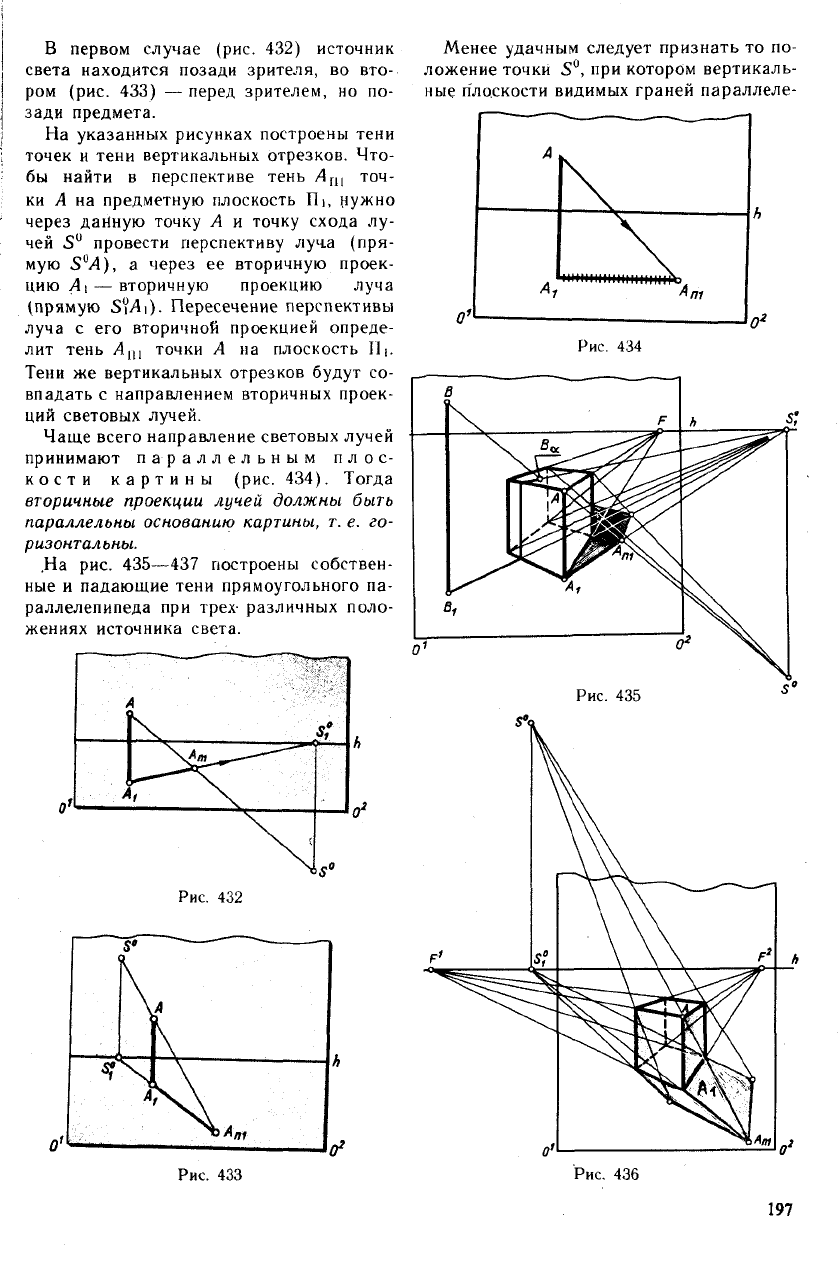
В первом случае (рис. 432) источник

света находится позади зрителя, во вто-

ром (рис. 433) — перед зрителем, но по-

зади предмета.

На указанных рисунках построены тени

точек и тени вертикальных отрезков. Что-

бы найти в перспективе тень Л

точ-

ки А на предметную плоскость П|, нужно

через данную точку А и точку схода лу-

чей S

провести перспективу луча (пря-

мую SM), а через ее вторичную проек-

цию А

— вторичную проекцию луча

(прямую S*Mi). Пересечение перспективы

луча с его вторичной проекцией опреде-

лит тень Ацj точки А на плоскость II|.

Тени же вертикальных отрезков будут со-

впадать с направлением вторичных проек-

ций световых лучей.

Чаще всего направление световых лучей

принимают параллельным плос-

кости картины (рис. 434). Тогда

вторичные проекции лучей должны быть

параллельны основанию картины,

т.

е. го-

ризонтальны.

.На рис. 435—437 построены собствен-

ные и падающие тени прямоугольного па-

раллелепипеда при трех- различных поло-

жениях источника света.

Менее удачным следует признать то по-

ложение точки S

, при котором вертикаль-

YV \ ?!

/ /

/ /'

/ /1

/ /'

/ /й

С&СЖ-1—)1

XTsV

V\ \ ^^

!\ Ъг

ll^wX

—tit?/ \

- O™"

' \

ч war \J

W <

Рис. 438

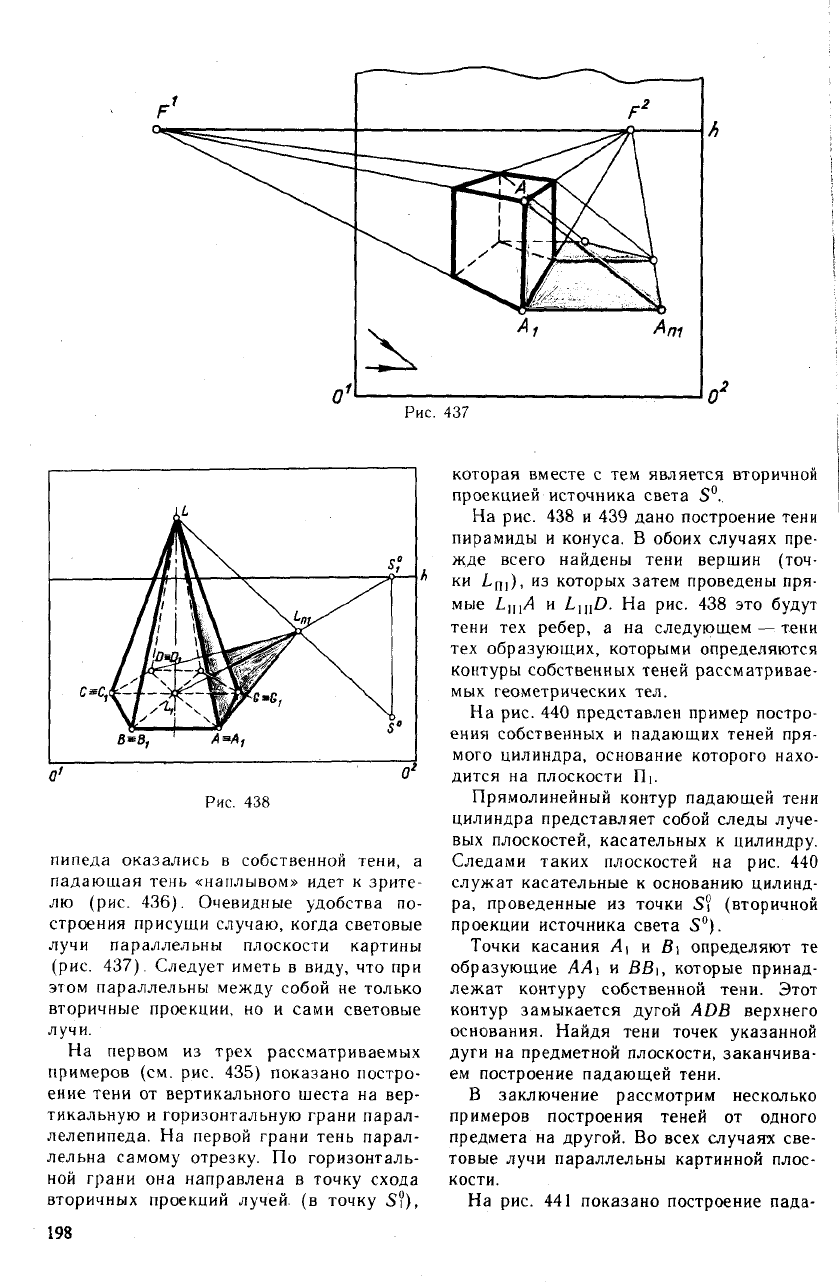
пипеда оказались в собственной тени, а

падающая тень «наплывом» идет к зрите-

лю (рис. 436). Очевидные удобства по-

строения присущи случаю, когда световые

лучи параллельны плоскости картины

(рис. 437). Следует иметь в виду, что при

этом параллельны между собой не только

вторичные проекции, но и сами световые

лучи.

На первом из трех рассматриваемых

примеров (см. рис. 435) показано постро-

ение тени от вертикального шеста на вер-

тикальную и горизонтальную грани парал-

лелепипеда. На первой грани тень парал-

лельна самому отрезку. По горизонталь-

ной грани она направлена в точку схода

вторичных проекций лучей (в точку S?),

которая вместе с тем является вторичной

проекцией источника света S

На рис. 438 и 439 дано построение тени

пирамиды и конуса. В обоих случаях пре-

жде всего найдены тени вершин (точ-

ки L

), из которых затем проведены пря-

мые L

A и L

D. На рис. 438 это будут

тени тех ребер, а на следующем — тени

тех образующих, которыми определяются

контуры собственных теней рассматривае-

мых геометрических тел.

На рис. 440 представлен пример постро-

ения собственных и падающих теней пря-

мого цилиндра, основание которого нахо-

дится на плоскости Пь

Прямолинейный контур падающей тени

цилиндра представляет собой следы луче-

вых плоскостей, касательных к цилиндру.

Следами таких плоскостей на рис. 440

служат касательные к основанию цилинд-

ра, проведенные из точки S? (вторичной

проекции источника света S

Точки касания А

и В\ определяют те

образующие АА\ и ВВ\, которые принад-

лежат контуру собственной тени. Этот

контур замыкается дугой ADB верхнего

основания. Найдя тени точек указанной

дуги на предметной плоскости, заканчива-

ем построение падающей тени.

В заключение рассмотрим несколько

примеров построения теней от одного

предмета на другой. Во всех случаях све-

товые лучи параллельны картинной плос-

кости.

На рис. 441 показано построение пада-

198

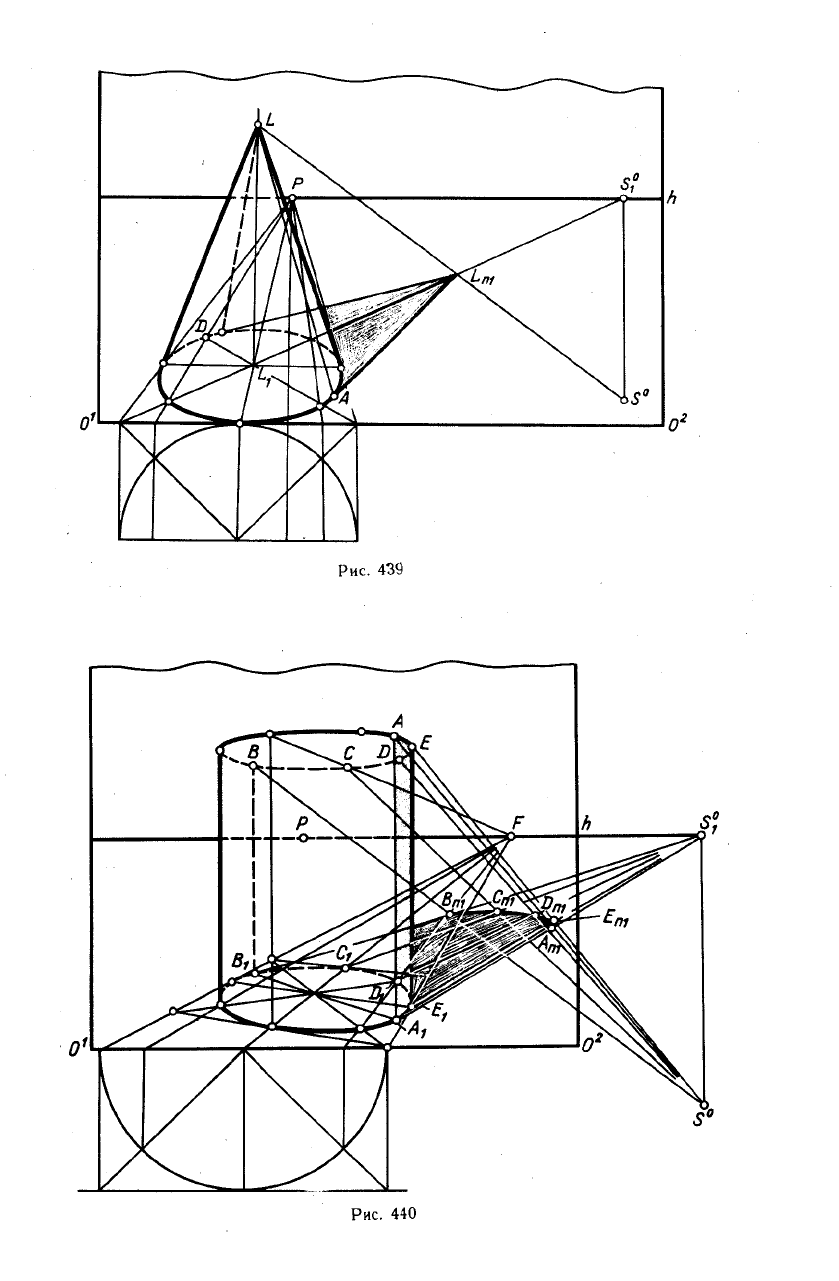
Рис. 320