Крылов Н.Н., ред. Начертательная геометрия
Подождите немного. Документ загружается.

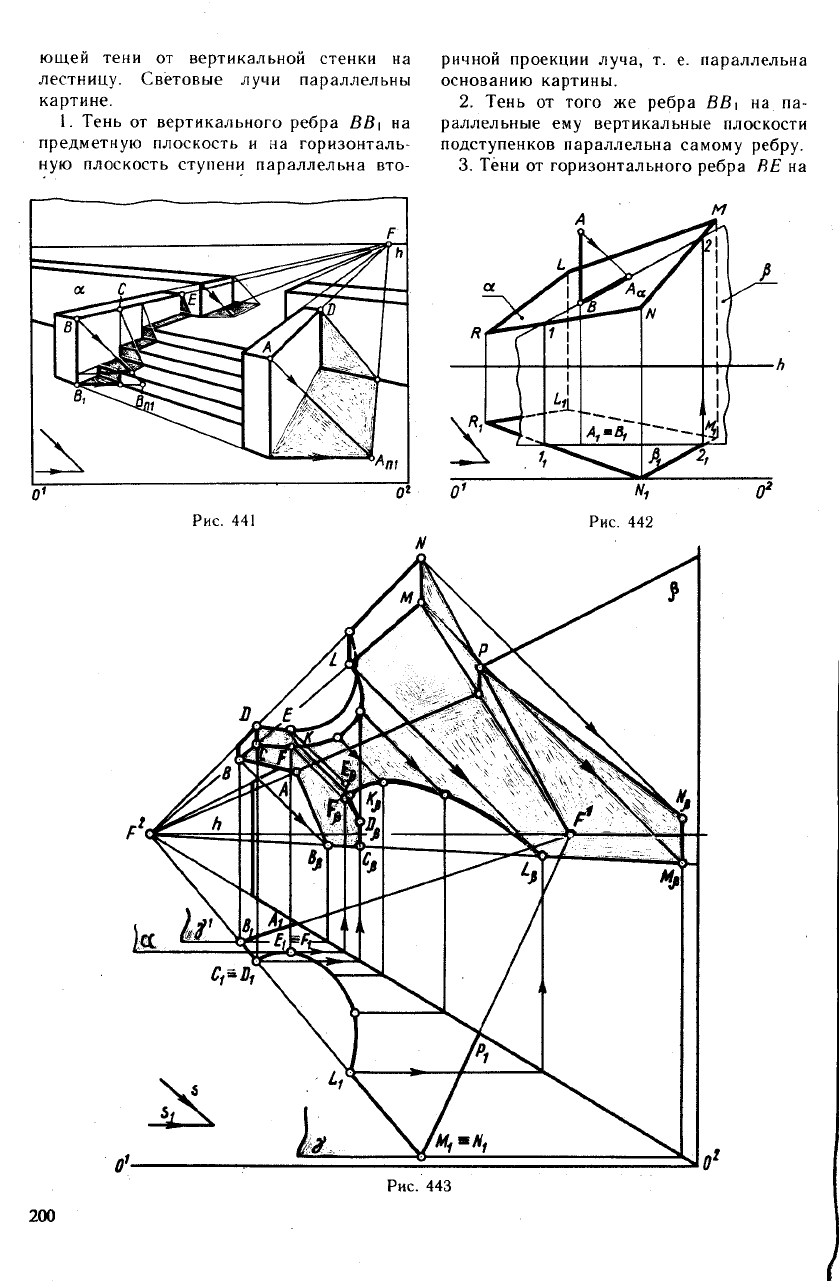
ющеи тени от вертикальной стенки на
лестницу. Световые лучи параллельны
картине.
1. Тень от вертикального ребра ВВ\ на
предметную плоскость и на горизонталь-
ную плоскость ступени параллельна вто-
ричной проекции луча, т. е. параллельна
основанию картины.
2. Тень от того же ребра ВВ\ на па-
раллельные ему вертикальные плоскости
подступенков параллельна самому ребру.
3. Тени от горизонтального ребра BE на
Рис. 300
200

параллельные ему плоскости ступеней
имеют общую точку схода с самим ребром.
4. Тени от ребра BE на плоскости под-
ступенков направлены к точкам, в которых
прямая BE пересекает продолженные
вверх плоскости подступенков. Одна из
таких точек (точка С) показана на
рис. 441.
Точно так же тени от ребер BE и AD на
вертикальную плоскость а пройдут через
точки пересечения указанных ребер с
плоскостью а.
Обратимся к рис. 442, на котором изо-
бражены перспективы ската кры-
ши LMNR и ребро трубы АВ.
Для построения тени этого ребра на
наклонном скате плоскости ос через свето-
вой луч проведена вспомогательная верти-
кальная плоскость р, след которой на
предметной плоскости совпадает со вто-
ричной проекцией луча (прямая 1\—2,).
Далее построена линия пересечения плос-
кости р и заданного ската а. Перспектива
этой прямой обозначена через 1—2, а вто-
ричная проекция — /1—2\.
Точка А
а
, в которой луч пересекает пря-
мую 1—2, является тенью точки А на на-
клонной плоскости ската. Соединив А
а
с
точкой В, получим искомую тень реб-
ра АВ.
На рис. 443 дано построение падающей
тени от козырька на вертикальной плоско-
сти стены р.
Сначала построена тень от козырька
в предположении, что в нем нет цилиндри-
ческого выреза. Для этого предварительно
определена его собственная тень и ее кон-
тур ABMNP (нижняя и правая грани ко-
зырька не освещены)..
Затем световые лучи, проходящие через
точки В, М и N, заключены в горизонталь-
но проецирующие плоскости у, у
1
и по-
строены вертикальные линии пересечения
этих плоскостей со стеной р. На этих ли-
ниях и будут расположены искомые те-
ни Bp, М$ и Np.
Ломаная линия AB$M$N$P является
контуром падающей тени козырька. Заме-
тим, что отрезок NpMp этого контура па-
раллелен NM, а параллельные друг другу
горизонтальные отрезки МрВц и MB име-
ют общую бесконечно удаленную точку,
перспектива F
2
которой расположена на
линии горизонта.
Для определения границы собственной
тени цилиндрической части выреза
козырька проведена горизонтально прое-
цирующая плоскость а, параллельная
картине и касающаяся вторичной проек-
ции цилиндрической поверхности в точ-
ке F\=E\.
В дальнейшем в плоскости р по отдель-
ным точкам построены падающие тени
от кривых DE и FL. В месте пересечения
этих теней определена точка а затем
с помощью обратного луча найдена точ-
ка К на кривой CFL. Кривая ЕК являет-
ся границей падающей тени на цилиндри-
ческой поверхности выреза козырька.
Построение падающей тени на повер-
хности прямого кругового цилиндра от
расположенного на нем навеса-пластины
показано на рис. 444. Световые лучи, про-
ходящие через точки горизонтальных ребер
АВ и ВС пластины, определяют две свето-
вые плоскости. Пересечение этих световых
плоскостей с цилиндрической поверхностью
Ф по эллиптическим кривым АЗ
Ф
В
Ф
и Вф2ф/
ф
и определяет искомый контур
падающей тени. Для его построения, так
же, как и в предыдущем примере
(см. рис. ч43), световые лучи, проходящие
через отдельные точки 1, 2, 3, В и т. д. ре-
бер АВ и ВС, были предварительно за-
ключены в вертикальные плоскости у, па-
раллельные картине. Эти плоскости пере-
секают данную цилиндрическую повер-
хность по вертикальным линиям — обра-
зующим цилиндра. Точки пересечения
этих образующих с соответствующи-
ми световыми лучами дают искомые
тени.
Касательная к цилиндру плоскость а
позволила установить границу собствен-
ной тени цилиндра.
Падающая на плоскость р тень от ко-
зырька найдена так же, как в предыдущем
примере (см. рис. 443). Точка О на реб-
ре FK определена с помощью обратного
луча, выходящего из точки Ор.
И наконец, рис. 445 иллюстрирует по-
строение падающей тени от вертикального
отрезка АВ на цилиндрическую повер-
хность Ф. Задача сводится к построению
линии пересечения световой плоскости ос,
проходящей через прямую АВ, с данной
цилиндрической поверхностью. Эта линия
строится по отдельным точкам 0, 1, 2, 3,
201
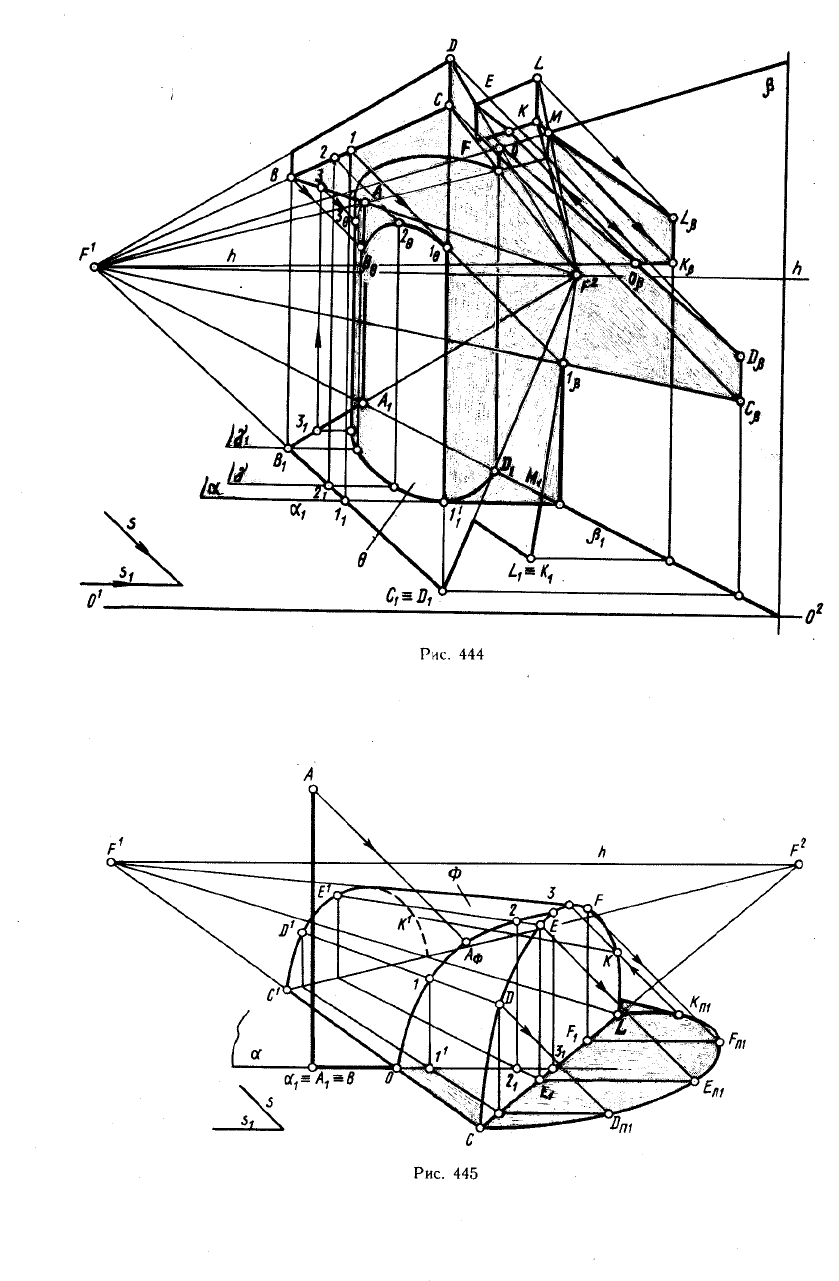
А

которые определяются пересечением со-
ответствующих образующих цилиндриче-
ской поверхности (СС
1
, DD\ ЕЕ
1
и др.) со
световой плоскостью а. Для нахождения
этих точек сначала определяют их вторич-
ные проекции, расположенные в месте пе-
ресечения вторичных проекций отмечен-
ных образующих со следом ai горизон-
тально-проецирующей плоскости а.
Луч, проходящий через точку А, дает
последнюю точку А
ф
падающей тени на
цилиндре.
Построение падающей тени от цилиндра
ясно из рисунка. Точка К
гп
касания пря-
молинейного контура падающей тени с
кривой LF
lu
E
ni
D
m
C позволяет с по-
мощью обратного луча определить ту об-
разующую цилиндра, которая является
границей его собственной тени (образую-
щая КК
1
).
§ 94. ТЕНИ В АКСОНОМЕТРИИ
Определение контуров падающих теней
в аксонометрии, по существу, ничем не от-
личается от того случая построения теней
в перспективе, когда световые лучи па-
раллельны плоскости картины.
Только в аксонометрии тень любой пря-
мой на плоскость, ей параллельную, па-
раллельна самой прямой. В перспективе
это имело место лишь в тех частных случа-
ях, когда прямая и плоскость были верти-
кальны или параллельны основанию кар-
тины.
Направление светового луча рекоменду-
ется определять диагональю куба, грани
которого совмещены с координатными
плоскостями, а ребра построены с учетом
коэффициентов искажения (рис. 446).
При этом диагонали граней куба являются
вторичными проекциями луча на коорди-
натные плоскости.
Следовательно, тень прямой, перпенди-
кулярной плоскости проекций, направлена
параллельно вторичной проекции луча на
ту же плоскость.
Так, тень A
t
A
U[
вертикального реб-
ра АА| направлена вдоль вторичной про-
екции луча на плоскость хОу (по диагона-
ли нижней грани), тень ребра АС (АС 1.
±хОг) определяется точками Лц
2
и С,
т. е. совпадает с вторичной проекцией лу-
ча на плоскость хОг.
На том же рисунке построена гень
AniC,
n
ребра АС на горизонтальную
плоскость.
Еще раз подчеркнем, что так как реб-
ро АС параллельно плоскости хОу, то
тень ребра.на эту плоскость параллельна
самому ребру. Отмеченные особенности
следует иметь в виду при решении кон-
кретных примеров.
Пример 1. На рис. 447 дана фронталь-
ная диметрия цилиндрической поверхно-
сти и двух касающихся ее вертикальных
плоскостей, ограниченных соответственно
линиями / и т.
Определение падающей тени следует
начать с построения теней линий / и т.
Тень каждой из них будет представлять
собой тени двух прямых, касающихся тени
полуокружности. Например, тень линии /
состоит из теней А
1
А
Ш
и В,6,,, двух вер-
тикальных прямых и тени Л|
И
С
т
В
т
по-
луокружности.
Общая касательная M,
m
JV
m
, к криволи-
нейным участкам контуров /
М|
и m
m
по-
зволяет с помощью обратных лучей опре-
делить границу собственной тени — обра-
зующую MN.
Этот контур собственной тени можно
построить и не прибегая к обратным лу-
чам.
В самом деле, искомая образую-
щая MN является той прямой, по которой
лучевая плоскость касается данной цилин-
дрической поверхности.
Известно, что решение задачи о прове-
дении плоскости, касательной к цилиндру
и параллельной данной прямой (в нашем
случае параллельной световому лучу), на-
чинается с построения вспомогательной
плоскости параллелизма. Плоскость па-
203
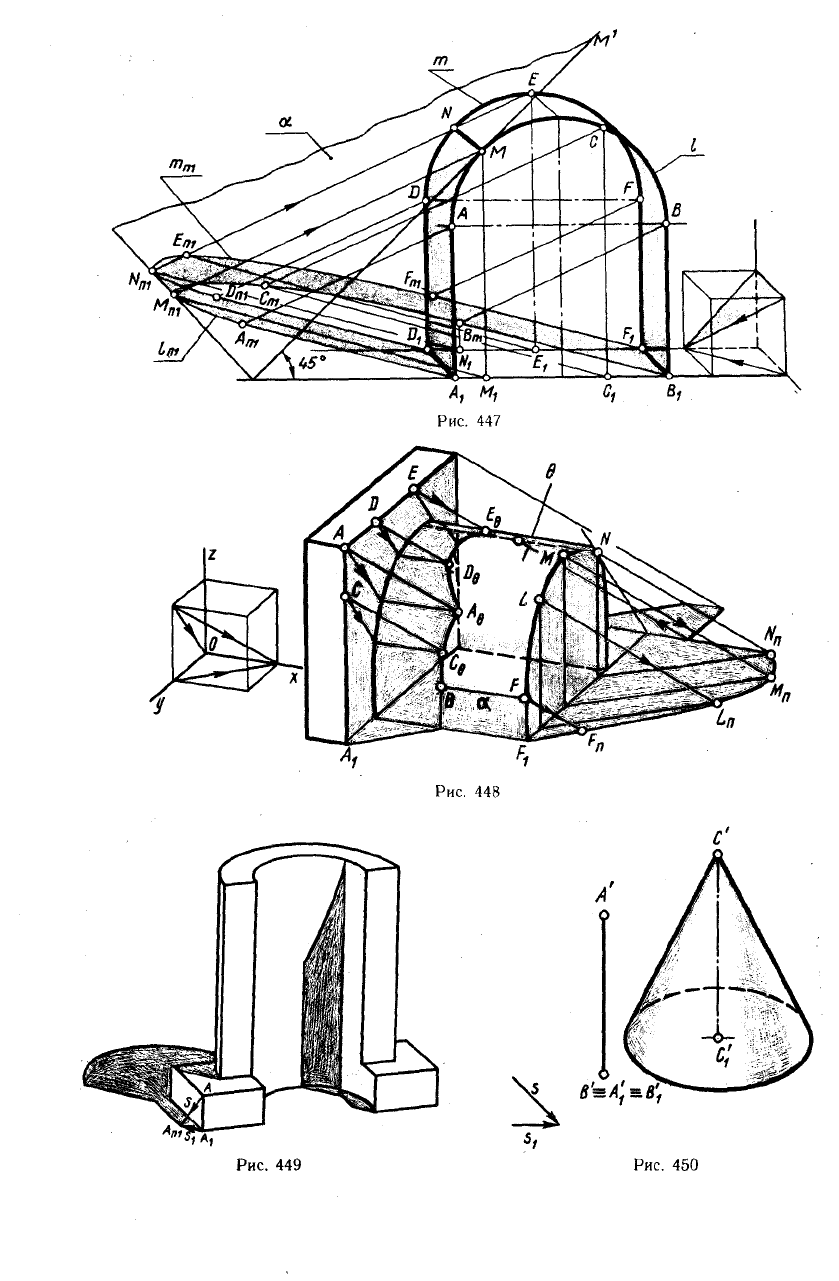
Рис. 448
Рис. 449 Рис. 450

раллелизма должна быть параллельна об-
разующим цилиндра и данной прямой.
На рис. 447 такая плоскость, выделен-
ная тоном, определена диагональю куба
(лучом) и тем горизонтальным ребром,
которое параллельно образующим цилин-
дрической поверхности. Тонированная
плоскость и фронтальная пересекаются по
прямой, составляющей с горизонтальной
плоскостью угол 45°.
Этот угол определяет направление
фронталей лучевой касательной плоско-
сти а.
На том же рисунке проведена фрон-
таль ММ
Х
как касательная к передней
полуокружности.
Найденная точка касания М позволяет
построить искомую образующую MN.
Описанный путь построения контура со-
бственной тени дает более точный резуль-
тат, чем тот, когда применяют обратные
лучи.
Пример 2. На рис. 448 показано постро-
ение теней группы геометрических тел. Из
видимых граней в собственной тени оказа-
лись правые.
Падающая тень вертикального реб-
ра АА\ по плоскости хОу направлена па-
раллельно вторичной проекции луча на эту
плоскость. Затем эта тень преломляется
и идет вертикально вверх по плоскости а
до точки В. При построении теней то-
чек А, С, D и Е на цилиндрической повер-
хности использованы вторичные проекции
светового луча на плоскость yOz. Тень
эллиптической дуги FLN представляет со-
бой множество точек, в которых световые
лучи, проходящие через точки дуги, пе-
ресекают координатную плоскость хОу.
Прямолинейным контуром падающей
тени цилиндра будет тень образующей, по
которой цилиндр и лучевая плоскость ка-
саются друг друга. На рис. 448 положение
этой образующей определено точкой N —
точкой касания правого основания цилин-
дра и прямой, проведенной параллельно
вторичной проекции луча на плос-
кость yOz.
Пример 3. На рис. 449 показана схема
здания в прямоугольной диметрии. На-
правление светового луча определено пря-
мой А А
а |,
которая, пересекаясь со своей
вторичной проекцией, дает падающую
тень А
л |
точки А на плоскости П|.
При заданном направлении светового
луча в собственной тени оказались левые
грани и часть цилиндрической поверхно-
сти. Построение падающих теней не вызы-
вает затруднений.
Вопросы и задачи для самоконтроля
1. Что представляет собой лучевая повер-
хность, ограничивающая контур собственной
тени шара, конуса, цилиндра?
2. Какая существует связь между контурами
собственной и падающей теней предмета?
3. При каком направлении светового луча
падающая тень конуса на плоскость его основа-
ния будет ограничена двумя параллельными
прямыми?
4. Построить падающую тень от отрезка АВ
на поверхности конуса (рис. 450).
5. Перечислите последовательность графиче-
ских операций при построении контуров падаю-
щей и собственной теней поверхности вращения
с криволинейной образующей.
6. При каком направлении световых лучей
перспектива Солнца и его вторичная проекция
не изображаются на картине?
7. Какими кривыми может быть ограничена
падающая тень сферы в перспективе?

РАЗДЕЛ 4
ИСПОЛЬЗОВАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
В ИНЖЕНЕРНОЙ ГРАФИКЕ
В данном разделе будут рассмотрены
вопросы использования современных
средств вычислительной техники и про-
граммного обеспечения при проектирова-
нии геометрической части (формы) раз-
личных объектов.
К сожалению, в связи с развитием
средств машинной графики получило рас-
пространение суждение о том, что изуче-
ние «ручных» способов формирования
проектной документации и чтения черте-
жей, а также их применения на практике
не является такой же важной задачей, как
в прошлые годы. Более того, в ряде учеб-
ных заведений пошли по пути сокращения
традиционных курсов начертательной
геометрии и черчения. Последствия таких
решений не заставили себя долго ждать.
У выпускников институтов резко упал
уровень пространственного воображения,
умения читать сложные чертежи, нахо-
дить верные проектные решения.
По мнению авторов учебника, гармо-
ничное сочетание способов обучения тра-
диционным методам и способам форми-
рования и чтения чертежей с изучением
сначала основ машинной графики, а за-
тем различных сложных графических си-
стем — наиболее приемлемый путь в ста-
новлении дисциплины «Инженерная гра-
фика».
Следует признать, что современный
уровень развития машинной графики —
технических и программных средств со-
здания, хранения, преобразования и отоб-
ражения графических объектов — позво-
ляет решать практически любую задачу
черчения и начертательной геометрии, ис-
ключая выполнение сложных ручных гра-
фических процедур.
Это позволяет освободить инженера-
проектировщика от решения большого
количества задач, связанных с формиро-
ванием изображений проектируемых
объектов, и получением проектной и про-
межуточной документации.
Низкая стоимость и высокая произ-
водительность современных персональ-
ных ЭВМ сделали доступными приме-
нение средств машинной графики и си-
стем проектирования на их базе пра-
ктически для каждого инженера-проекти-
ровщика.
В настоящее время разработано боль-
шое количество качественных профессио-
нальных программных комплексов для
создания и отображения геометрических
объектов. Такие комплексы называют по-
разному: графические редакторы, систе-
206

мы машинной графики, графические си-
стемы и т. п. На их базе строятся многие
программные системы, предназначенные
для проектирования объектов различного
назначения.
Наиболее распространенными про-
граммными комплексами машинной гра-
фики являются AutoCad, 3D-StudioMax,
(CorelDraw). Обладая большими возмож-
ностями, достаточно сложным интерфей-
сом (языком общения пользователя с си-
стемой), специализированными языками
программирования, средствами связи
с другими системами, эти программные
продукты требуют довольно продолжи-
тельного изучения. Поэтому изложение
возможностей и способов взаимодейст-
вия с какой-либо из перечисленных си-
стем не является целью настоящей главы.
Вместе с тем большинство графических
систем при создании как плоских, так
и пространственных геометрических
объектов используют ряд общих принци-
пов. Сведения о них содержатся в данном
разделе, и с ними полезно познакомиться
при изучении традиционного курса начер-
тательной геометрии.
ГЛАВА 18
РАБОТА С ПЛОСКИМИ
ОБЪЕКТАМИ
§ 95. СИСТЕМА КООРДИНАТ.
ЕДИНИЦЫ ИЗМЕРЕНИЯ. КУРСОР
Любая работа, связанная с формирова-
нием графического объекта, начинается
с задания формы, размеров и системы
кооринат области пространства, где бу-
дет размещаться будущий объект.
Для двумерных объектов — это, как
правило, прямоугольная область с декар-
товой системой координат. Для трехмер-
ных объектов — это, обычно, область,
имеющая форму параллелепипеда и де-
картова система координат, определяе-
мая тремя взаимно перпендикулярными
осями.
Здесь необходимо заметить, что при-
вычное для нас вертикальное расположе-
ние оси Z в большинстве зарубежных про-
граммных системах машинной графики
(так же как и в переводной литературе)
не соблюдается.
Расположение начала координат в за-
даваемой области может быть произ-
вольным, но, обычно, его размещают или
в левом нижнем углу, или посередине.
Размеры задаваемой области определя-
ются габаритами объекта и могут быть,
как правило, изменены пользователем.
В некоторых системах эти размеры меня-
ются автоматически по мере увеличения
габаритов формируемого объекта.
Так как формируемый геометрический
объект имеет, в конечном счете, реальные
размеры, на начальном этапе работы не-
обходимо также задать единицы измере-
ния, с которыми в дальнейшем будет ра-
ботать графическая система.
Некоторые системы являются «безраз-
мерными», авторы которых справедливо
полагают, что вопрос задания единиц из-
мерения может быть решен на этапе по-
лучения твердой копии — чертежа на
бумаге.
При формировании геометрического
объекта пользователь должен иметь до-
ступ к произвольной точке заданной об-
ласти. Этот доступ можно обеспечить не-
посредственным вводом координат точки
с использованием клавиатуры. Однако,
несмотря на заманчивую возможность
избежать неточностей, этот способ неудо-
бен, особенно когда процедура определе-
ния положения точки выполняется много-
кратно.
В интерактивном режиме* работы гра-
фических систем (практически все
графические системы имеют такой ре-
жим) для указания конкретной точки
в области формирования графического
объекта используется специальный указа-
тель — курсор. Положением курсора
управляет пользователь посредством
устройства «мышь» и (или) клавишами-
стрелками.
Положение, которое занимает курсор
в данный момент времени, называется те-
кущим положением, а координаты точки,
на которуюкурсор указывает, — текущи-
ми координатами. Текущие координаты
курсора обычно отображаются в углу эк-
*Интерактивный режим реализует принцип
«вижу то, что делаю». Альтернативным режи-
мом является «пакетный», реализующий прин-
цип «вижу только конечный результат».
207

рана и динамически меняются при пере-
мещении курсора в области формирова-
ния объекта.
Как правило, курсор имеет форму
длинного (во весь экран) или короткого
перекрестия. В некоторых системах кур-
сор выполнен в виде стрелки, изображе-
ния указательного пальца и т. п. В других
системах форму курсора может задавать
сам пользователь. В любом случае курсор —
удобное средство идентификации точки
в области создания объекта.
§ 96. ПЛОСКИЕ ГРАФИЧЕСКИЕ
ПРИМИТИВЫ. КОМПОНОВКА
ПЛОСКИХ ИЗОБРАЖЕНИЙ
Любой плоский графический объект
можно представить как совокупность
простых графических элементов, называ-
емых примитивами. Каждая графическая
система имеет собственный набор таких
графических примитивов, из которых
строятся более сложные объекты. Вместе
с тем ряд примитивов является общим
для всех систем. К ним относятся отрезки
прямых линий, окружности и их дуги,
кольца, эллипсы, прямоугольники, мно-
гоугольники, текстовые строки, кривые
линии.
Каждый графический примитив имеет
набор характеристик (атрибутов), кото-
рые могут быть изменены пользователем.
К основным атрибутам примитивов от-
носятся:
• координаты опорных точек
• цвет
• толщина линии
• тип линии
• тип и размер шрифта (для тексто-
вых строк).
ОТРЕЗОК ПРЯМОЙ ЛИНИИ,
ЛОМАНАЯ ЛИНИЯ
Опорными точками отрезков служат
его крайние точки. После задания пер-
вой опорной точки от нее за перемеща-
ющимся по экрану курсором тянется
так называемая «резиновая нить» —
прямая линия, соединяющая первую
опорную точку и текущее положение ку-
рсора.
После того как положение второй точ-
ки отрезка зафиксировано, отрезок счита-
ется заданным, он появляется на экране
со всеми своими атрибутами, и можно
переходить к вводу следующего графичес-
кого примитива. При задании ломаной
линии каждая вторая опорная точка пре-
дыдущего отрезка служит началом после-
дующего.
ОКРУЖНОСТЬ
Окружность на плоскости задается дву-
мя точками — центром и произвольной
точкой, лежащей на окружности. Иногда
последовательность ввода этих точек ме-
няется. В большинстве систем при за-
дании графических примитивов существу-
ет возможность сочетать ввод с испо-
льзованием «мыши» и клавиатуры. На-
пример, можно задавать окружности,
указывая их центры курсором, а значение
радиуса вводить с клавиатуры.
ДУГА ОКРУЖНОСТИ
Способы задания дуг окружностей бо-
лее разнообразны в различных графичес-
ких системах, хотя принципиально не от-
личаются друг от друга. Наиболее рас-
пространенной является следующая по-
следовательность задания опорных точек
дуги: начало дуги, центр окружности, ко-
торой принадлежит дуга, конечная точка,
определяющая луч, выходящий из центра
окружности и отсекающий дугу в ее ко-
нечной точке. Направление построения
дуги (по часовой стрелке или против нее)
фиксировано и определяется самой гра-
фической системой.
ПРЯМО УГОЛЬНИК
Опорными точками прямоугольника
служат противоположные его вершины.
Стороны прямоугольника параллельны
сторонам рамки, ограничивающей об-
ласть построения графического объекта.
КРИВЫЕ ЛИНИИ
Многие графические системы позволя-
ют задавать ряд регулярных кривых ли-
ний — дуги эллипсов, параболы, гипер-
болы и т. п. Кроме того, имеется возмож-
ность использования встроенных функций
сглаживания ломаных линий, построения
208

плавных линий, проходящих через зада-
ваемые точки, построения сопряжений
и т. д. Наиболее сложные кривые можно
задавать непосредственно, используя
устройство «мышь».
ТЕКСТОВЫЕ СТРОКИ
Текстовые строки являются неотъемле-
мой частью графических объектов, осо-
бенно плоских чертежей. Их обычно не
рассматривают как графические примити-
вы, хотя в большинстве графических си-
стем ввод текстов включен в группу ко-
манд ввода графических примитивов. Ат-
рибутами текстовых строк, кроме цвета
и опорной точки, являются параметры,
характерные только для этого типа эле-
ментов графического объекта. К ним от-
носятся высота шрифта, ориентация стро-
ки относительно границ области форми-
рования графического объекта, угол на-
клона символов, тип шрифта, его качест-
во (как правило, жирность). Все эти ат-
рибуты должны быть установлены пред-
варительно, до ввода самой строки.
Практически любой плоский графичес-
кий объект может быть сформирован на
основе того набора графических прими-
тивов, который имеется в распоряжении
графической системы.
Способ формирования объекта, ско-
рость его описания зависят от конкрет-
ного пользователя графической системы,
его опыта и квалификации. Помимо стан-
дартных графических примитивов, каж-
дый опытный пользователь формирует
свой собственный набор графических эле-
ментов, которыми оперирует при созда-
нии графических объектов определенного
класса.
§ 97. ОКОННЫЕ ФУНКЦИИ
Под окном, обычно, понимают прямо-
угольную область, которая может быть
отображена на экране монитора. Ею мо-
жет быть или часть плоского графичес-
кого объекта, или часть проекции про-
странственного объекта. Размеры окна
могут не быть пропорциональны рабочей
области (области отображения) экрана,
однако вывод окна всегда производится
жность всегда останется окружностью,
а квадрат — квадратом.
Каждая графическая система обладает
гибкой системой оконных функций, по-
зволяющих, с одной стороны, обеспечить
необходимый уровень проработки каж-
дой детали формируемого объекта,
а с другой — оценивать весь объект цели-
ком, оперировать с его отдельными ча-
стями. Благодаря наличию оконных функ-
ций становится возможным формировать
достаточно большие по размеру сложные
и насыщенные графические объекты, ис-
пользуя даже небольшую рабочую об-
ласть экрана дисплея.
ПОКАЗАТЬ ВСЕ
Функция «Показать все» выводит в ра-
бочую область экрана весь графический
объект. При этом многие его мелкие дета-
ли могут быть или не показаны, или сли-
ваться с другими деталями. Тем не менее,
эта функция очень полезная: она позволя-
ет оценить весь объект целиком или пе-
рейти к заданию части объекта, с которой
предполагается дальнейшая работа.
ЗАДАНИЕ ОКНА ПРОСМОТРА
(ЗАДАНИЕ ОКНА В ОКНЕ)
Окно просмотра задается внутри теку-
щего окна — той части графического
объекта, которая в данный момент отоб-
ражена на экране монитора. Для задания
окна просмотра необходимо определить
любые противоположные углы прямоу-
гольной области, после чего окно будет
автоматически отображено на экране.
ВОЗВРАТ К ПРЕДЫДУЩЕМУ ОКНУ
Эта функция удобна при отработке
мелких деталей графического объекта,
расположенных в разных частях текущего
окна.
Задав окно в окне и выполнив необ-
ходимые операции с мелкими элемента-
ми, можно вернуться к исходному окну
и задать в другом его месте новое окно.
На рис. 451 показан фрагмент черте-
жа,служащий исходным окном. Штрихо-
выми линиями выделены два прямоу-
гольных окна.
209
