Крупкина Т.В. Математическая статистика. Практикум
Подождите немного. Документ загружается.


Гипотеза о среднем. H
0
: a = a
0
.
Статистическая модель Статистика Z Z
/H
0
hN(a, σ
0
)i
(¯x−a
0
)
√
n
σ
0
N(0, 1)
hN(a, σ)i
(¯x−a
0
)
√
n
¯s
T
n−1
Критерии для проверки гипотез о параметрах двух независимых
распределений. Рассматриваются 2 независимые случайные величины и
выборки наблюдений этих величин X, Y :
X = {(x
1
, . . . , x
n
1
)} ∈ N(a
1
, σ
1
), Y = {(y
1
, . . . , y
n
2
)} ∈ N(a
2
, σ
2
).
Гипотеза о дисперсии. H
0
: σ
1
= σ
2
.
Модель Статистика Z Z
/H
0
hN(a
0
, σ)i, hN(a, σ)i
(¯s
1
)
2
(¯s
2
)
2
, s
1
> s
2
. F
n
1
−1,n
2
−1
Замечание. Критерий, использующий данную статистику для провер-
ки данной гипотезы, называется критерием Фишера.
Гипотеза о средних. H
0
: a
1
= a
2
Модель Статистика Z Z
/H
0
hN(a, σ
0
)i
(известны σ
1
, σ
2
)
¯x−¯y
r
σ
2
1
n
1
+
σ
2
2
n
2
N(0, 1)
hN(a, σ)i(σ
1
, σ
2
неиз-
вестны, но гипотеза
H
0
: σ
1
= σ
2
не отвер-
гается)
¯x−¯y
r
¯s
2
1
(n
1
−1)+¯s
2
2
(n
2
−1)
n
1
+n
2
−2
(
1
n
1
+
1
n
2
)
√
T
n
1
+n
2
−2
hN(a, σ)i(σ
1
, σ
2
неиз-
вестны, и гипотеза H
0
:
σ
1
= σ
2
отвергается)
¯x−¯y
r
¯s
2
1
n
1
+
¯s
2
2
n
2
T
ν
,
где ν ≈
¯s
2
1
n
1
+
¯s
2
2
n
2
2
¯s
2
1
n
1
!
2
n
1
+1
+
¯s
2
2
n
2
!
2
n
2
+1
−2
Замечание. Критерий, использующий статистику, отмеченную галочкой
(
√
), называется критерием Стьюдента.
71

Гипотеза о средних для парных совокупностей. Рассматривают-
ся 2 случайные величины и выборки наблюдений этих величин X, Y : X =
{(x
1
, . . . , x
n
)} ∈ N(a
1
, σ
1
), Y = {(y
1
, . . . , y
n
)} ∈ N(a
2
, σ
2
), причем X
i
и Y
i
связаны, например, через объект наблюдения. Перейдем к разности случай-
ных величин; тогда d = X −Y, d ∈ N(a
d
, σ
d
). Очевидно, a
d
= a
1
−a
2
. Обычно
σ
d
неизвестно. Гипотеза H
0
: a
1
= a
2
∼ H
0
: a
d
= 0.
Модель Статистика Z Z
/H
0
hN(a, σ)i
¯
d
√
n
¯s
d
=
P
d
i
√
n−1
n
P
d
2
i
−(
P
d
i
)
2
T
n−1
Замечание. Этот критерий называется критерием Стьюдента для парных
выборок.
Пример 42. По выборке из нормального распределения N(a, 3) объема
n = 139 со средним x = 9, 193 проверить гипотезу о том, что пара-
метр a равен 9.
J
1. Пусть α = 0, 05.
hN(a, σ
0
)i, σ
0
= 3.
H
0
: a = 9; H
1
: a 6= 9.
2. В нашем примере параметр a, оценка параметра – X, известно рас-
пределение функции
Z(x) =
(X − a)
√
n
σ
0
.
3. Если верна H
0
: a = 9, то Z(x) ∈ N(0, 1). Если же верна H
1
:
a = a
1
6= 9, то распределение X ∈ N(a
1
, σ
0
) смещено влево или вправо
относительно распределения X при нулевой гипотезе N(9, σ
0
), значит, так
же смещено и распределение Z(x) =
(X−a)
√
n
σ
0
. Поэтому критическая область
двусторонняя:
V = {x : Z(x) 6 u
0,025
или Z(x) > u
0,975
},
то есть
V = {x : Z(x) 6 −1, 96} ∪ {x : Z(x) > 1, 96}.
4.
Z(x) =
(
X − a)
√
n
σ
0
;
72

Z
в
=
(9, 193 − 9)
√
139
3
≈ 0, 758;
5. Z
в
не попадает в критическую область V , поскольку −1, 96 <
0, 758 < 1, 96. Следовательно, с уровнем значимости α = 0, 05 нулевая гипо-
теза H
0
не отвергается.
6. Вывод: данная выборка может быть взятой из совокупности с мате-
матическим ожиданием 9 I.
Пример 43. Проверить гипотезу о том, что среднеквадратичное
отклонение цены на товар σ = 1, 4, если по 101 наблюдению S = 1, 2.
J
1. Можно использовать нормальную модель; уровень значимости α за-
дадим равным 0,05. Сформулируем гипотезы:
H
0
: σ
ξ
= σ
0
= 1, 4; H
1
: σ
ξ
= σ
1
< 1, 4
2. Воспользуемся статистикой
Z =
nS
2
σ
2
0
,
при условии H
0
статистика Z имеет распределение χ
2
n−1
.
3. Найдем критическую область V . Так как σ
1
< σ
0
, то при верной ги-
потезе H
1
статистика Z =
nS
2
σ
2
0
принимает меньшие значения, чем при вер-
ной гипотезе H
0
, следовательно, критическая область левосторонняя: V =
{x : Z(x) 6 χ
2
α
}. Из таблиц находим граничное значение Z
крит
= χ
2
100;0,05
=
77, 929. Таким образом, критическая область V = [0; 77, 929].
4. Рассчитаем по выборке значение статистики Z
в
:
Z
в
=
nS
2
σ
2
0
=
101 · (1, 2)
2
(1, 4)
2
≈ 74, 2
5. Поскольку Z
в
= 74, 2 < 77, 929 = Z
крит
, то Z
в
попадает в критиче-
скую область V , следовательно нулевая гипотеза отвергается в пользу аль-
тернативной с уровнем значимости α = 0, 05.
6. Таким образом, нельзя считать, что среднеквадратичное отклонение
цены на товар σ = 1, 4. Следует признать, что оно меньше.I
Задачи
73

Замечание. Если в условиях не указан уровень значимости α, следует
задать его самим.
295. По выборке из нормального распределения объема n = 400
проверить гипотезу о том, что выборка взята из распределения с
математическим ожиданием 14. Дисперсия известна и равна 81. Рас-
считанное по выборке среднее ¯x = 13, 6.
296. При решении контрольной работы средняя оценка в бал-
лах по курсу равна a
0
= 13. В одной из групп (26 студентов) сред-
няя оценка равна ¯x = 11, S = 2. Можно ли считать, что работа
в данной группе выполнена хуже, или отклонение следует считать
случайным? (α = 0, 05.)
297. Урожайность культуры составляет 35 центнеров с гекта-
ра; на 10 опытных делянках ¯x = 38 центнеров с гектара, s
2
= 49.
Случайно ли превышение урожайности?
298. Средние по отрасли издержки на производство единицы
некоторого товара составляют a
0
= 23, а по 50 предприятиям кор-
порации выборочное среднее издержек равно ¯x = 20, S = 2. Можно ли
считать, что издержки в данной корпорации ниже, или отклонение
следует считать случайным? (α = 0, 05.)
299. В условиях примера 37 проверить гипотезу о том, что
математическое ожидание курса английского фунта стерлингов за
упомянутый период равно a = 50.
300. При измерении производительности двух агрегатов полу-
чены следующие результаты:
A : 14, 1 10, 1 14, 7 13, 7 14, 0; B : 14, 0 14, 5 13, 7 12, 7 14, 1.
Различна ли их производительность?
301. Одинаково ли потребление сырья для производства продук-
та при двух технологиях, если n
1
= 16,
¯
S
2
1
= 8, ¯x = 6; n
2
= 36,
¯
S
2
2
=
15, ¯y = 7?
302. n
1
= 21,
¯
S
2
1
= 25, n
2
= 31,
¯
S
2
2
= 16. Проверить гипотезу о том,
что σ
2
1
6= σ
2
2
при α = 0, 1.
303. Производительность труда в дневную смену описана дан-
ными: n
1
= 16, ¯x = 14, 5,
¯
S
2
1
= 4; в ночную смену: n
2
= 16, ¯y = 13,
¯
S
2
2
= 3.
Можно ли считать, что ночная работа менее эффективна?
74
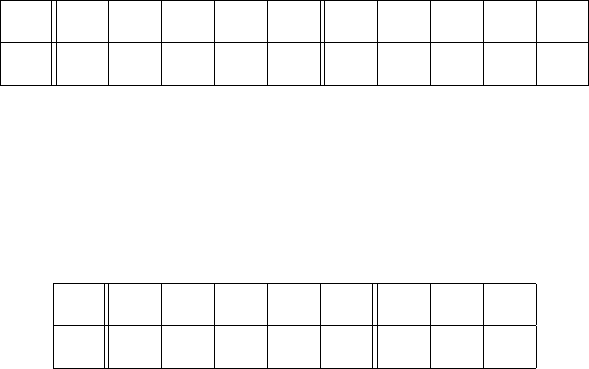
304. X – производительность при работе с перерывом, Y – без
перерыва, измеренная у одних и тех же 10 человек. Проверить гипо-
тезу a
Y
< a
X
. Уровень значимости положить равным 0,05.
X 40 35 41 55 46 60 51 43 62 41
Y 30 30 38 21 49 53 31 27 53 48
305. У группы студентов проверялись знания элементарной ма-
тематики через полгода (X) и через полтора года ( Y ) после окон-
чания школы (max = 100 баллов). Проверить гипотезу о том, что
знания не изменились. Уровень значимости положить равным 0,1.
X 50 88 71 55 46 80 87 53
Y 40 63 75 41 49 57 71 27
306. Указаны выборочные дисперсии размеров прибыли при про-
изводстве товаров двух групп: n
1
= 40, S
2
1
= 36; n
2
= 50, S
2
2
= 49.
Можно ли считать, что прибыль при производстве товаров первой
группы колеблется сильнее, или различия следует считать случайны-
ми? (α = 0, 05.)
307. Выборка X = (124, 90, 124, 99, 90, 111, 89) представляет собой
значения индексов продаж 7 однотипных товаров некоторого про-
изводителя. Проверить гипотезу о том, что средний индекс продаж
для товаров данного производителя равен среднему индексу продаж,
рассчитанному по товарам всех производителей и принимаемому за
100 (α = 0, 05).
308. При стабильном процессе в камере поддерживает-
ся температура 25, 5
◦
. Путем измерений получена выборка:
25, 43; 25, 41; 25, 44; 26, 20; 25, 60; 25, 59; 25, 62; 25, 53; 25, 52; 25, 53. Про-
верить гипотезу о среднем (α = 0, 01).
309. Среднее значение показателя воздушного загрязнения
окружающей среды для двигателя равно 20. При стабильном про-
цессе в камере поддерживается температура 25, 5
◦
. Дана выбор-
ка значений этого показателя для 10 двигателей нового типа:
15, 6; 16, 2; 22, 5; 20, 5; 16, 4; 19, 4; 16, 6; 17, 9; 12, 7; 13, 9. Проверить гипоте-
зу о том, что у двигателей нового типа показатель воздушного за-
грязнения окружающей среды ниже (α = 0, 01).
75

§ 14. Непараметрические критерии
Гипотеза о виде распределения. H
0
: F (x) = F
0
(x).
Критерии, проверяющие гипотезу о виде распределения, называются
критериями согласия.
Критерий согласия Колмогорова. Пусть x = (x
1
, . . . , x
n
) – выборка
из генеральной совокупности с неизвестной функцией распределения F (x).
Выдвинута простая гипотеза H
0
: F (x) = F
0
(x), где F
0
(x) задана. Критерий
согласия Колмогорова применяют для непрерывных функций распределения
F (x).
В качестве статистики критерия выбирают величину
D
n
= D
n
(x) = sup
x
|(F
n
(x) − (F(x)|, (9)
а в качестве критической области – область вида
V = (t
∗
, ∞), (10)
где t
∗
табулировано. Так, t
∗
= t
∗
α
= 1, 3581 при α = 0, 05; t
∗
α
= 1, 6276
при α = 0, 01. Таким образом, при заданном уровне значимости α правило
проверки гипотезы H
0
при n > 20 сводится к следующему:
если значение статистики
ˆ
t = D
n
(x) = max
x
|F
∗
n
(x)−F
0
(x)|удовлетво-
ряет неравенству
√
n ·
ˆ
t > t
∗
,
то H
0
отвергают, в противном случае делают вывод, что статистические дан-
ные не противоречат гипотезе.
Критерий согласия χ
2
Пирсона. Критерий согласия χ
2
Пирсона так-
же проверяет гипотезу H
0
: F (x) = F
0
(x), но его можно применять для лю-
бых распределений. Чтобы воспользоваться этим критерием, выборочные
данные предварительно группируют. Пусть n
i
– число значений, попавших
в i-й интервал, i = 1, . . . , k, n – объем выборки, p
i
– теоретическая веро-
ятность попадания одного элемента выборки в i-й интервал. Однако в тео-
ретическом распределении могут быть неизвестные параметры (θ
1
, . . . , θ
r
),
что обычно и встречается на практике. Тогда по выборке (x
1
, . . . , x
n
) перво-
начально находят оценки (θ
∗
1
, . . . , θ
∗
r
) и затем по F (x, θ
∗
1
, . . . , θ
∗
r
) вычисляют
теоретические вероятности p
i
.
Статистика критерия
Z =
k
X
i=1
(n
i
− np
i
)
2
np
i
∼ χ
2
ν
, (11)
76

где ν = k − r − 1 – число степеней свободы. Ограничения: n > 50 и np
i
> 4.
Критическую область задаем в виде V = (t
∗
, ∞), значение t
∗
– квантиль
распределения χ
2
ν
порядка (1 − α).
Таким образом, вид критерия согласия χ
2
:
если значение статистики Z
в
удовлетворяет неравенству
Z
в
> t
∗
,
гипотезу H
0
отвергают, в противном случае гипотеза H
0
не противоречит
условиям испытаний.
Пример 44. Фирма предлагает 3 вида продукта. По данным прошло-
го года вероятности заказов для разных видов соответственно рав-
ны 0,1; 0, 65; 0,25. В этом году из 600 покупателей 42 приобрели про-
дукт первого вида, 365 – второго, 193 – третьего. Можно ли счи-
тать, что предпочтения покупателей не изменились?
J Проверим гипотезу H
0
: F (x) = F
0
(x), где F
0
обозначает распределение
вероятностей по данным прошлого года. Составим таблицу:
Вид продукта 1 2 3
Число покупок n
i
42 365 193
p
i
0, 1 0, 65 0, 25
np
i
60 390 150
Здесь n = 600, p
i
– теоретическая вероятность покупки продукта i-го вида,
i = 1, 2, 3.
Z
в
=
3
X
i=1
(n
i
− np
i
)
2
np
i
=
=
(42 − 60)
2
60
+
(365 − 390)
2
390
+
(193 − 150)
2
150
= 19, 33.
Пусть α = 0, 015.
t
∗
= χ
2
l−r−1; 0,99
= χ
2
3−0−1; 0,95
= χ
2
2; 0,99
= 9, 21034
(последнее значение нашли по таблице).
Z
в
> t
∗
,
следовательно, гипотезу H
0
отвергают и следует считать, что предпочтения
покупателей изменились.I
77

Пример 45. Было проведено 1000 измерений случайной величины η,
равной времени ожидания ответа на запрос, измеренному в долях
от теоретически возможного максимального времени, принятого за
единицу. Требуется выяснить распределение этой величины.
J Сгруппируем данные:
№ Интервал Численность n
i
n
i
n
n
i
nh
P
n
i
n
1 0, 00 − 0, 09 80 0,080 0,007 0,080
2 0, 09 − 0, 18 81 0,081 0,007 0,161
3 0, 18 − 0, 27 93 0,093 0,008 0,254
4 0, 27 − 0, 36 85 0,085 0,008 0,339
5 0, 36 − 0, 45 87 0,087 0,008 0,426
6 0, 45 − 0, 54 87 0,087 0,008 0,513
7 0, 54 − 0, 63 87 0,087 0,008 0,600
8 0, 63 − 0, 72 106 0,106 0,010 0,706
9 0, 72 − 0, 81 99 0,099 0,009 0,805
10 0, 81 −0, 90 89 0,089 0,008 0,894
11 0, 90 −0, 99 106 0,106 0,010 1,000
По рассмотрении таблицы группировки можно выдвинуть гипотезу о
равномерном распределении. Параметры этого распределения найдем с по-
мощью оценивания:
ˆa = y
min
= x
∗
1
= 0,
ˆ
b = x
max
= x
∗
n
≈ 1.
H
0
: F
η
(y) = F
R[0,1]
(y).
Применим критерий согласия χ
2
Пирсона.
В качестве статистики критерия возьмем величину
Z =
k
X
i=1
(n
i
− np
i
)
2
np
i
,
где p
i
– теоретическая вероятность попадания одного элемента выборки в
i-й интервал, равная 0,1. После вычислений получаем Z
в
= 9, 25.
Критическая область V
k
= (χ
2
k−r−1,1−α
, +∞), где r – число парамет-
ров, оцененных в выборке. У нас r = 2, в таблице значений квантилей рас-
пределения χ
2
находим χ
2
8,0.95
= 15, 51. Так как значение Z
в
не попало в
критическую область, то гипотеза H
0
не отвергается, то есть статистические
данные не противоречат гипотезе о том, что величина η имеет распределение
R[0, 1]. I
78
Пример 46. В условиях предыдущего примера проверим гипотезу с по-
мощью критерия согласия Колмогорова.
J H
0
: F
η
(y) = F
R[0,1]
(y).
В качестве статистики критерия возьмем величину
D
n
=
√
n · max
y
F
∗
n
(y) − F
R[0,1]
(y)
.
После вычислений мы получили D
n
= 1, 22. Так как критическая область для
α = 0, 05 равна V
k
= (1, 36; +∞), a значение D
n
не попадает в критическую
область, то гипотеза H
0
не отвергается, то есть можно считать, что величина
η имеет распределение R[0, 1] I
Задачи
310. Доказать состоятельность критерия Колмогорова.
311. В эксперименте Бюффона при n = 4040 бросаниях монеты
наблюдалось m = 2048. Согласуются ли эти данные с гипотезой о сим-
метричности монеты при уровне значимости α, равным: а) 0,05; б)
0,1.
312. При n = 1000 независимых испытаний с исходами A
1
, A
2
, A
3
эти события осуществились соответственно 350, 320 и 330 раз. Про-
верить, согласуются ли эти данные при уровне значимости 0,05 с ги-
потезой H
0
: p
1
= p
2
= p
3
, где p
i
= P(A
i
).
313. В таблице приводятся результаты 100 опытов, состоящих
в одновременном подбрасывании 6 костей. В каждом из опытов под-
считывалось число m костей, выпавших кверху гранью с шестью оч-
ками.
m 0 1 2 3 4 5 6
n
i
47 35 8 9 1 0 0
Проверить гипотезу правильности костей.
314. Можно ли считать равномерным распределение студентов
по знакам Зодиака?
Номер знака 1 2 3 4 5 6
n
i
12 13 23 11 9 10
Номер знака 7 8 9 10 11 12
n
i
15 7 15 9 7 3
79
315. В десятичной записи числа π среди первых 10 002 знаков по-
сле запятой цифры 0, 1, ..., 9 встречаются соответственно 968, 1026,
1021, 974, 1014, 1046, 1021, 970, 948, 1014 раз. Можно ли при уровне
значимости 0,05 считать эти цифры случайными? При каком уровне
значимости эта гипотеза отвергается?
316. Датчик случайных чисел выдал 10 000 чисел 0, 1, . . . , 9. Среди
них числа, превосходящие 5, встретились 5105 раз. Проверить гипо-
тезу о случайности чисел.
317. Проверить гипотезу H
0
: F = P
λ
;
m 0 1 2 3 4 5
n
i
13 17 12 5 3 1
318. По официальным данным в Швеции в 1935 г. родилось 88 273
ребенка, причем в январе родилось 7280 детей, в феврале – 6957, мар-
те – 7883, апреле – 7884, мае – 7892, июне – 7609, июле – 7585, ав-
густе – 7393, сентябре – 7203, октябре – 6903, ноябре – 6552 и в де-
кабре – 7132 ребенка. Совместимы ли эти данные с гипотезой, что
день рождения наудачу выбранного человека с равной вероятностью
приходится на любой из 365 дней года?
319. В экспериментах с селекцией гороха Мендель наблюдал ча-
стоты различных видов семян, полученных при скрещивании расте-
ний с круглыми желтыми семенами и растений с морщинистыми зе-
леными семенами. Эти данные и значения теоретических вероятно-
стей по теории наследственности приведены в следующей таблице:
Семена Частота Вероятность
Круглые и желтые 315 9/16
Морщинистые и желтые 101 3/16
Круглые и зеленые 108 3/16
Морщинистые и зеленые 32 1/16
Проверить гипотезу H
0
о согласии частот с теоретическими веро-
ятностями (на уровне значимости α = 0, 1).
320. В таблице приведены числа n
i
участков равной площади 0,25
км
2
южной части Лондона, на каждый из которых приходилось по i
80
