Крупкина Т.В. Математическая статистика. Практикум
Подождите немного. Документ загружается.


§ 3. Группировка выборки. Графические
характеристики
Метод группировки выборки объема n. Число интервалов k реко-
мендуется брать из условия 2
k−1
∼ n. Длина интервала h =
x
max
−x
min
k
. Гра-
ницы интервалов группировки: x
0
= x
min
, x
i
= x
0
+ hi, i = 1, ..., k, далее
подсчитывается, сколько элементов выборки попало в каждый интервал, и
в группировочной таблице заполняется столбец «Численность n
i
». Осталь-
ные столбцы рассчитываются по столбцу численностей. Они пригодятся при
построении графических характеристик.
Таблица 2
Таблица группировки
№ Интервал Численность n
i
n
i
n
n
i
nh
i
P
1
n
j
n
1 [x
0
− x
1
)
2 [x
1
− x
2
)
. . . . . .
Гистограмма – это фигура, состоящая из прямоугольников, построен-
ных на интервалах группировки как на основаниях и имеющих площади
n
i
n
,
для чего берут высоту прямоугольника, равную
n
i
nh
.
Полигон – это ломаная линия, проходящая через середины верхних
границ прямоугольников гистограммы (соединяющая точки (x
∗
i
;
n
i
nh
, где x
∗
i
–
середина i-го интервала). Полигон и гистограмма являются статистическими
аналогами теоретической плотности.
Кумулята – это ломаная линия, соединяющая точки (x
i
;
i−1
P
1
n
j
n
). Куму-
лята дает представление о графике функции распределения.
Для нахождения приближенных значений выборочных медианы, мо-
ды и квантилей по группированной выборке применяют интерполяционные
формулы.
Медианным называется интервал, в котором накопленная сумма ча-
стот впервые достигает
1
2
.
Выборочной группированной медианой называется значение m
∗
e
:
m
∗
e
= x
e
+
n/2 − (n
1
+ . . . + n
m
e
−1
)
n
m
e
· h,
21
где n – объем выборки, h – длина интервала группировки, x
e
– левая гра-
ница медианного интервала, n
i
– численность i-го интервала, n
m
e
– числен-
ность медианного интервала.
Модальным называется интервал, имеющий наибольшую числен-
ность.
Выборочной группированной модой называется значение m
∗
0
:
m
∗
0
= x
0
+ h ·
n
m
0
− n
m
0
−1
2n
m
0
− n
m
0
−1
− n
m
0
+1
,
где x
0
– левая граница модального интервала, n
m
0
– численность модаль-
ного интервала, n
m
0
−1,
, n
m
0
+1
– численности интервалов слева и справа от
модального.
Квантильным порядка q интервалом называется интервал, в котором
сумма накопленных частот впервые достигает значения q.
Выборочной группированной квантилью называется значение x
∗
q
:
x
∗
q
= x
(q)
+ h ·
nq − (n
1
+ ··· + n
(q)−1
)
n
(q)
,
где x
(q)
– левая граница квантильного интервала, n
(q)
– численность кван-
тильного интервала, n
1
, ··· , n
(q)−1
– численности интервалов, предшеству-
ющих квантильному.
Пример 12. Произвести группировку выборки:
87, 8 104, 5 90, 9 92, 4 74, 3 71, 7 75, 0 92, 0 76, 0 82, 2
86, 3 85, 0 75, 0 91, 5 105, 7 112, 4 80, 8 74, 5 86, 6 95, 8
100, 4 109, 7 52, 7 96, 6 87, 6 101, 4 103, 4 90, 6 88, 0 79, 9
91, 6 84, 2 108, 6 77, 5 89, 2 82, 6 90, 0 86, 1 80, 3 92, 8
103, 8 84, 5 90, 6 113, 5 101, 1 113, 7 94, 3 90, 7 70, 7 93, 5
96, 8 111, 5 103, 8 106, 8 80, 5 91, 8 82, 2 86, 9 100, 3 100, 1
89, 4 84, 7 93, 4 101, 3 118, 7 99, 3 105, 0 92, 7 96, 7 82, 8
100, 9 81, 3 96, 1 84, 6 86, 3 83, 7 84, 6 80, 7 102, 3 104, 2
89, 4 90, 9 89, 6 66, 5 120, 4 100, 4 86, 8 70, 4 91, 9 98, 3
111, 7 90, 2 87, 9 81, 1 88, 1 103, 3 85, 0 69, 1 82, 2 101, 8
80, 4 77, 7 79, 3 96, 2 94, 1 87, 6 104, 2 81, 4 81, 6 115, 7
84, 2 93, 2 112, 7 86, 8 79, 8 89, 8 88, 1 110, 9 109, 0 84, 8
82, 6 89, 1 88, 9 97, 9 78, 0 87, 5 68, 1 107, 7 95, 5 88, 6
J 1. Упорядочим выборку (получим вариационный ряд).
22

52, 7 66, 5 68, 1 69, 1 70, 4 70, 7 71, 7 74, 3 74, 5 75, 0
75, 0 76, 0 77, 5 77, 7 78, 0 79, 3 79, 8 79, 9 80, 3 80, 4
80, 5 80, 7 80, 8 81, 1 81, 3 81, 4 81, 6 82, 2 82, 2 82, 2
82, 6 82, 6 82, 8 83, 7 84, 2 84, 2 84, 5 84, 6 84, 6 84, 7
84, 8 85, 0 85, 0 86, 1 86, 3 86, 3 86, 6 86, 8 86, 8 86, 9
87, 5 87, 6 87, 6 87, 8 87, 9 88, 0 88, 1 88, 1 88, 6 88, 9
89, 1 89, 2 89, 4 89, 4 89, 6 89, 8 90, 0 90, 2 90, 6 90, 6
90, 7 90, 9 90, 9 91, 5 91, 6 91, 8 91, 9 92, 0 92, 4 92, 7
92, 8 93, 2 93, 4 93, 5 94, 1 94, 3 95, 5 95, 8 96, 1 96, 2
96, 6 96, 7 96, 8 97, 9 98, 3 99, 3 100, 1 100, 3 100, 4 100, 4
100, 9 101, 1 101, 3 101, 4 101, 8 102, 3 103, 3 103, 4 103, 8 103, 8
104, 2 104, 2 104, 5 105, 0 105, 7 106, 8 107, 7 108, 6 109, 0 109, 7
110, 9 111, 5 111, 7 112, 4 112, 7 113, 5 113, 7 115, 7 118, 7 120, 4
2. Минимальный элемент выборки равняется x
min
= 52, 7, а макси-
мальный x
max
= 120, 4.
Определим сначала число интервалов k. Рекомендуется брать такое k,
что 2
k−1
∼ n.
В данном примере n = 130.
2
7
= 128 ∼ 130; k − 1 = 7, k = 8.
Выберем число интервалов k = 8.
3. Определим длину интервала h.
h =
x
max
− x
min
k
.
Находим
h =
120, 4 − 52, 7
8
≈ 8, 4567.
4. Найдем границы интервалов группировки x
0
= x
min
, x
i
= x
0
+hi, i =
1, ..., k:
x
0
= 52, 7, x
1
= 61, 2, x
2
= 69, 6, x
3
= 78, 1, x
4
= 86, 5,
x
5
= 95, 0, x
6
= 103, 4, x
7
= 111, 9, x
8
= 120, 4.
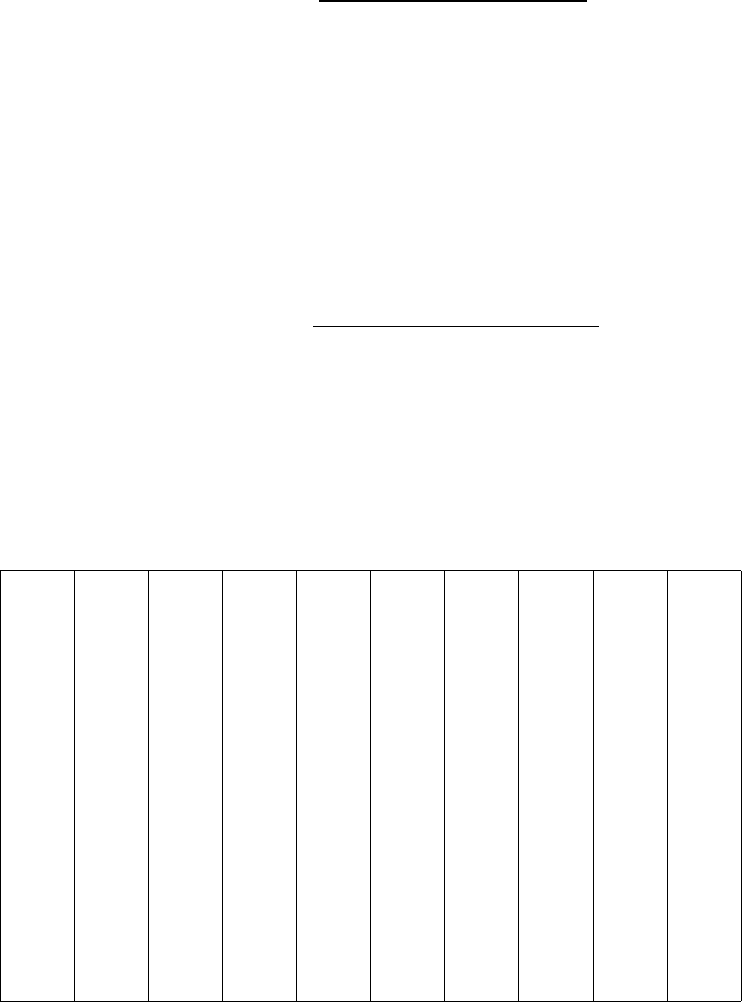
5. Составим таблицу группировки и внесем границы интервалов в стол-
23

бец «Интервал»:
№ Интервал n
i
n
i
n
P
i
1
n
j
n
1 [52, 7 − 61, 2)
2 [61, 2 − 69, 6)
3 [69, 6 − 78, 1)
4 [78, 1 − 86, 5)
5 [86, 5 − 95, 0)
6 [95, 0 −103, 4)
7 [103, 4 − 111, 9)
8 [111, 9 − 120, 4)
6. Подсчитаем, сколько элементов выборки попало в каждый интервал,
и заполним в таблице столбец «Численность n
i
»:
№ Интервал n
i
n
i
n
P
i
1
n
j
n
1 [52, 7 − 61, 2) 1
2 [61, 2 − 69, 6) 3
3 [69, 6 − 78, 1) 11
4 [78, 1 − 86, 5) 31
5 [86, 5 − 95, 0) 40
6 [95, 0 −103, 4) 22
7 [103, 4 − 111, 9) 15
8 [111, 9 − 120, 4) 7
По столбцу численностей рассчитаем остальные столбцы таблицы:
№ Интервал n
i
n
i
n
P
i
1
n
j
n
1 [52, 7 − 61, 2) 1 0, 008 0, 008
2 [61, 2 − 69, 6) 3 0, 023 0, 031
3 [69, 6 − 78, 1) 11 0, 085 0, 115
4 [78, 1 − 86, 5) 31 0, 238 0, 354
5 [86, 5 − 95, 0) 40 0, 308 0, 662
6 [95, 0 −103, 4) 22 0, 169 0, 831
7 [103, 4 − 111, 9) 15 0, 115 0, 946
8 [111, 9 − 120, 4) 7 0, 054 1
I
24

Пример 13. По группированной выборке, полученной в примере 12,
найти выборочную медиану.
№ Интервал n
i
n
i
n
P
i
1
n
j
n
1 [52, 7 − 61, 2) 1 0, 008 0, 008
2 [61, 2 − 69, 6) 3 0, 023 0, 031
3 [69, 6 − 78, 1) 11 0, 085 0, 115
4 [78, 1 − 86, 5) 31 0, 238 0, 354
5 [86, 5 − 95, 0) 40 0, 308 0, 662
6 [95, 0 −103, 4) 22 0, 169 0, 831
7 [103, 4 − 111, 9) 15 0, 115 0, 946
8 [111, 9 − 120, 4) 7 0, 054 1
J Медианным является интервал № 5, так как в нем впервые накопленная
сумма частот, равная 0,662, достигает
1
2
.
m
∗
e
= 86, 5 +
130/2 − (1 + 3 + 11 + 31)
40
· 8, 4567 ≈ 90, 517. I
Задачи
60. Произвести группировку выборки:
20, 2; 19, 2; 16, 9; 19, 3; 17, 1; 17, 8; 16, 6; 16, 3; 15, 2; 18, 0; 16, 8; 20, 0;
17, 7; 16, 6; 19, 0; 17, 5; 17, 8; 20, 6; 17, 2; 18, 0; 17, 1; 18, 4; 17, 4; 15, 8;
19, 4; 17, 8; 19, 8; 19, 6; 16, 3; 20, 0; 17, 4; 19, 3; 19, 3; 16, 5; 18, 8; 17, 2;
18, 7; 18, 6; 19, 2; 16, 2; 18, 2; 17, 4.
61. По выборке, данной в виде статистического ряда, построй-
те гистограмму, полигон и кумуляту.
X 0 − 6 6 −12 12 − 18 18 − 24
n
i
1 8 10 6
25
В задачах 62–64 постройте по выборке гистограмму и полигон и по их
виду подберите статистическую модель.
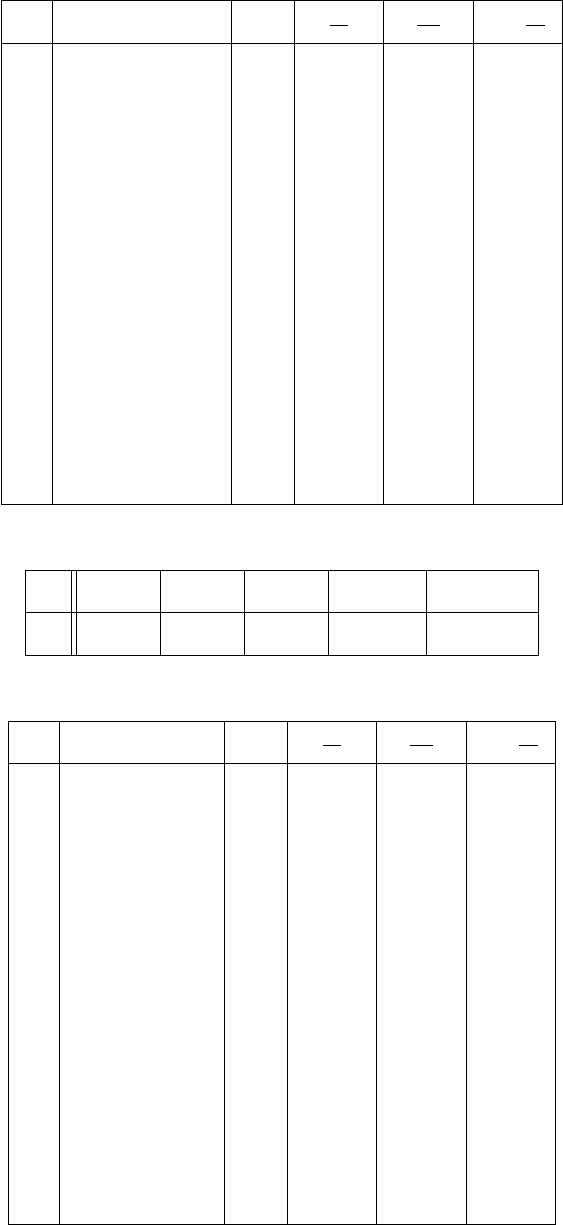
62.
№ n
i
n
i
n
n
i
nh
P
n
i
n
1 0, 01 −0, 98 260 0, 260 0, 252 0, 260
2 0, 98 −1, 94 340 0, 340 0, 329 0, 600
3 1, 94 −2, 91 192 0, 192 0, 186 0, 792
4 2, 91 −3, 88 101 0, 101 0, 098 0, 893
5 3, 88 −4, 85 63 0, 063 0, 061 0, 956
6 4, 85 −5, 81 20 0, 020 0, 019 0, 976
7 5, 81 −6, 78 16 0, 016 0, 015 0, 992
8 6, 78 −7, 75 3 0, 003 0, 003 0, 995
9 7, 75 −8, 72 4 0, 004 0, 004 0, 999
10 8, 72 − 9, 68 0 0, 000 0, 000 0, 999
11 9, 68 −10, 65 1 0, 001 0, 001 1, 000
63.
X 0 − 3 3 −6 6 − 9 9 − 12 12 − 15
n
i
2 8 12 6 3
64.
№ n
i
n
i
n
n
i
nh
P
n
i
n
1 0, 00 − 0, 09 80 0, 080 0, 007 0, 080
2 0, 09 − 0, 18 81 0, 081 0, 007 0, 161
3 0, 18 − 0, 27 93 0, 093 0, 008 0, 254
4 0, 27 − 0, 36 85 0, 085 0, 008 0, 339
5 0, 36 − 0, 45 87 0, 087 0, 008 0, 426
6 0, 45 − 0, 54 87 0, 087 0, 008 0, 513
7 0, 54 − 0, 63 87 0, 087 0, 008 0, 600
8 0, 63 − 0, 72 106 0, 106 0, 010 0, 706
9 0, 72 − 0, 81 99 0, 099 0, 009 0, 805
10 0, 81 −0, 90 89 0, 089 0, 008 0, 894
11 0, 90 −0, 99 106 0, 106 0, 010 1, 000
65. По двумерной выборке найти выборочные распределения
26
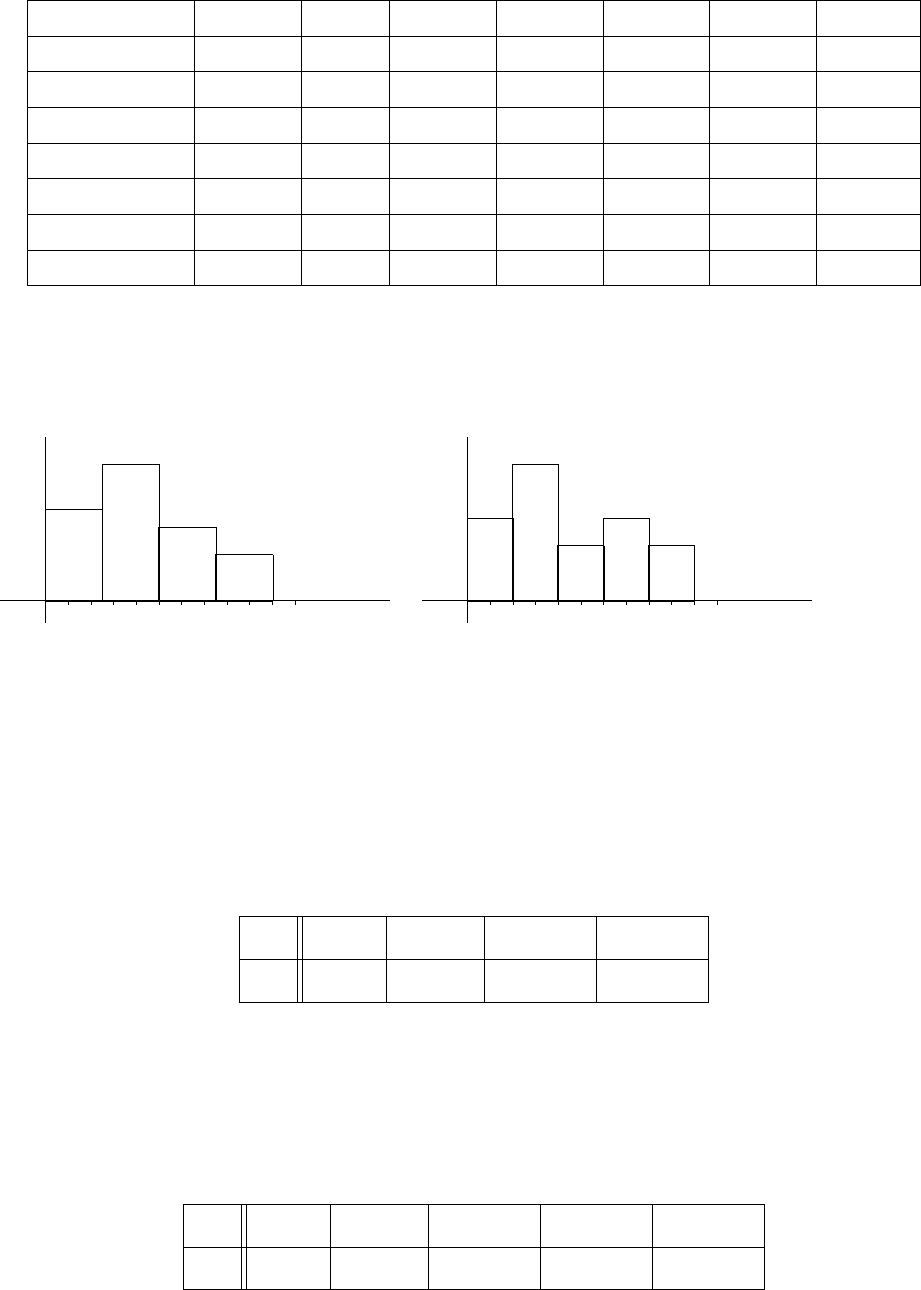
компонент, построить для каждой из них гистограмму и полигон,
подобрать статистическую модель.
XY [−0.9; 0) [0; 0.9) [0.9; 1.8) [1.8; 2.7) [2.7; 3.6) [3.6; 4.5) [4.5; 5.4]
[−1.53; −0.75) 0 0 4 0 0 0 0
[−0.75; 0.03) 0 5 1 3 3 2 0
[0.03; 0.81) 0 2 6 7 6 0 1
[0.81; 1.59) 2 3 9 10 6 1 1
[1.59; 2.37) 0 0 4 5 4 4 1
[2.37; 3.15) 1 0 5 1 0 1 0
[3.15; 3.93) 0 0 0 0 1 1 0
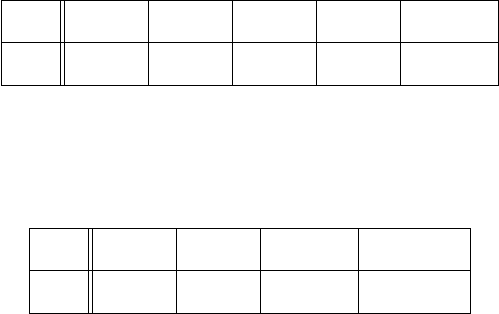
66. Могут ли графики (1) и (2) (рис. 2) являться гистограммами
одной и той же выборки?
x
-
1 2
3
4
5 6
7
8 9 10
6
0
x
-
1 2
3
4
5 6
7
8 9 10
6
0
8/75
0,1
Рис. 2. Гистограммы (1) и (2)
67. Приведите (если это возможно) примеры выборок, для ко-
торых а) приведенный на рис. 2 график (1) является гистограммой,
а график (2) не является; б) график (1) не является гистограммой, а
график (2) является гистограммой.
68. Дан группированный статистический ряд величины Х:
X 0 − 6 6 −12 12 − 18 18 − 24
n
i
2 7 5 6
Найти приближенно моду и медиану.
69. Для группированного статистического ряда из предыдущей
задачи найти приближенно квантили порядков 0,2 и 0,8.
70. Дан группированный статистический ряд величины Х:
X 0 − 5 5 −10 10 − 15 15 − 20 20 − 25
n
i
4 8 9 7 4
27
Найти приближенно моду и медиану.
71. Для группированного статистического ряда из предыдущей
задачи найти приближенно квантили порядков 0,25 и 0,75.
72. Вычислить поправку Шеппарда для третьего начального мо-
мента по группированному статистическому ряду из предыдущей
задачи.
73. Вычислить поправку Шеппарда для второго начального мо-
мента по группированному статистическому ряду
X 0 − 2 2 −4 4 − 6 6 − 8 8 − 10
n
i
2 3 6 5 4
74. Вычислить поправку Шеппарда для выборочной дисперсии по
группированному статистическому ряду
X 3 − 6 6 −9 9 − 12 12 − 15
n
i
7 6 4 3
28
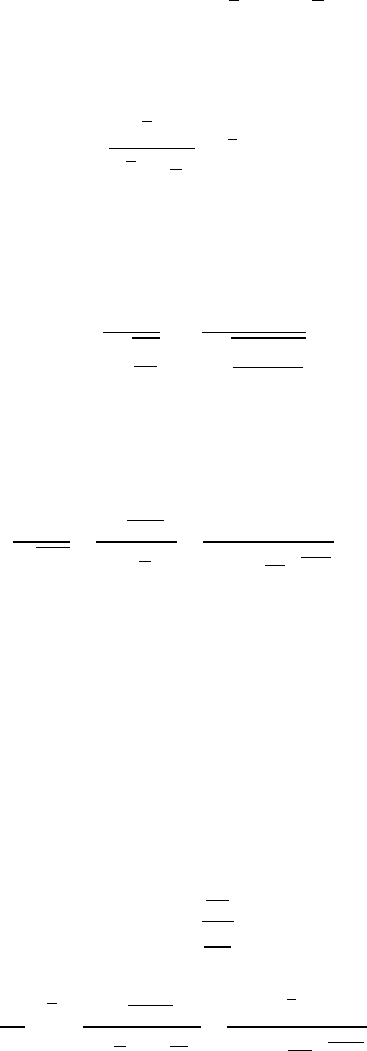
§ 4. Распределения χ
2
, Стьюдента,
Фишера
Статистикой можно назвать любую функцию элементов выборки
T (X) = T (X
1
, . . . , X
n
), которая не зависит от параметров распределения.
Распределением хи-квадрат χ
2
n
с n степенями свободы называется
гамма-распределение с параметрами α =
1
2
, β =
n
2
.
Соответствующая случайная величина обозначается тем же символом
χ
2
n
, а ее плотность имеет вид
f
ξ
2
(x) =
x
n
2
−1
2
n
2
Γ(
n
2
)
e
−
x
2
, x > 0.
Распределением Стьюдента T
n
с n степенями свободы называется
распределение случайной величины
t
n
=
ξ
q
χ
2
n
n
=
ξ
q
P
n
i=1
ξ
2
i
n
,
где ξ, ξ
i
∈ N(0, 1) и независимы.
Формула плотности распределения Стьюдента
f
T
n
(x) =
1
√
πn
·
Γ(
n+1
2
)
Γ(
n
2
)
·
1
(1 +
x
2
n
)
n+1
2
, x ∈ R,
где Γ(β) – гамма-функция, определяемая для всех β > 0 соотношением
Γ(β) =
∞
Z
0
t
β−1
e
−t
dt.
Распределением Фишера (Фишера–Снедекора, F -распределением)
с n, m степенями свободы называется распределение случайной величины
f
n,m
=
χ
2
n
n
χ
2
m
m
.
f
F
n,m
(x) =
n
m
n
2
·
Γ(
n+m
2
)
Γ(
n
2
)Γ(
m
2
)
·
x
n
2
−1
(1 +
nx
m
)
n+m
2
, x ∈ R
+
.
Пример 14. Изобразить квантили уровней α/2 и 1 − α/2 на графике
плотности распределения χ
2
n
.
29
J
0
χ
2
n,1−α/2
χ
2
n,α/2
f
χ
2
n
(x)
X
Рис. 3. Квантили уровней α/2 и 1 − α/2 на графике плотности распределения χ
2
n
I
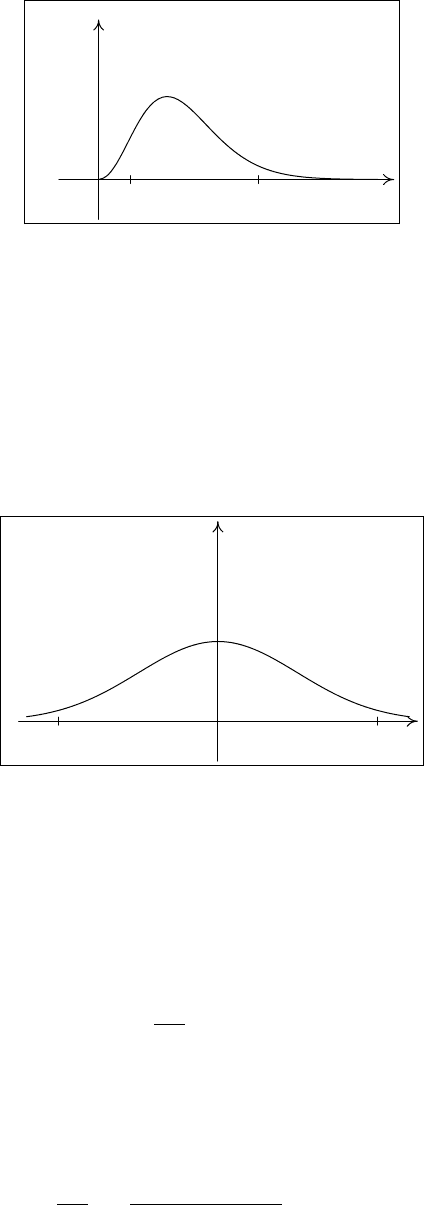
Пример 15. Изобразить квантили уровней α/2 и 1 − α/2 на графике
плотности распределения T
n
.
J
0
f
T
n
(x)
XT
n,α/2
T
n,1−α/2
Рис. 4. Квантили уровней α/2 и 1 −α/2 на графике плотности распределения Стьюдента T
n
I
Пример 16. Доказать, что
χ
2
n
n
p
−→ 1.
J Пусть ξ
1
, . . . , ξ
n
независимы и имеют стандартное нормальное рас-
пределение. Тогда E ξ
2
i
= Dξ = 1, и по ЗБЧ
χ
2
n
n
=
ξ
2
1
+ . . . + ξ
2
n
n
p
−→ 1.
I
30
