Крупкина Т.В. Математическая статистика. Практикум
Подождите немного. Документ загружается.


б) X ± 2, 575
σ
0
√
n
;
в) X ± 0, 99
σ
0
√
n
.
254. Вывести формулу доверительного интервала для σ в
N(a, σ).
255. В модели N(a, σ) рассчитать доверительные интервалы для
a и σ по данным: ¯x = 103, S
2
= 16, n = 26, α = 0, 1.
256. Решить предыдущую задачу в модели N(a, 3) (параметр σ
известен и равен 3).
257. В модели N(a, σ) рассчитать доверительные интервалы для
a и σ по данным: ¯x = 5, S
2
= 4, n = 9, α = 0, 05.
258. В модели N(a, σ) рассчитать доверительный интервал для
σ по выборке (2, 3, 3, 1, 1, 2, 4, 2, 1, 3) при α = 0, 1.
259. Решить предыдущую задачу, если параметр a известен и
равен 2.
260. Найти доверительные интервалы для θ в моделях N(θ, 1) и
N(1, θ).
261. Найти доверительный интервал для p в B(N, P ).
262. Найти доверительный интервал для λ в P
λ
.
263. В равномерном распределении R[0, b] найти доверительный
интервал для b.
264. В модели R[0, b] показать, что интервал (X
∗
n
,
X
∗
n
n
√
α
) является
доверительным интервалом для b значимости α.
265. В равномерном распределении R[a, 0] найти доверительный
интервал для a.
266. В равномерном распределении R[−θ, θ] найти доверитель-
ный интервал для θ.
267. В модели N(3, σ) найти доверительный интервал для σ по
выборке: (1, 2, 2, 3, 3, 3, 3, 4, 5) при α = 0, 1.
268. Найти доверительный интервал для θ в N(θ, θ).
269. Найти доверительный интервал для θ
3
в N(θ, σ
0
).
270. Найти асимптотически кратчайший доверительный ин-
тервал для α в Γ(α, β).
61

271. Найти доверительный интервал для α в распределении с
плотностью
f(x) = e
α−x
x > 0.
272. Найти доверительный интервал для отношения дисперсий
двух нормальных моделей.
273. Будет ли в нормальной модели hN
θ
1
,θ
2
i интервал (0;
|x|
u
1+α
0
2
),
построенный по одному наблюдению x, являться доверительным ин-
тервалом для θ
2
значимости α < α
0
?
62

§ 12. Статистические гипотезы
Статистической гипотезой (или просто гипотезой) называется лю-
бое утверждение о виде или свойствах распределения наблюдаемых в экспе-
рименте случайных величин. Статистическая гипотеза называется простой,
если однозначно фиксирует распределение наблюдений. Иначе это сложная
гипотеза. Проверяемая гипотеза называется нулевой (H
0
). Любая гипотеза
о распределении наблюдаемой случайной величины, которая может оказать-
ся истинной, но отличается от основной гипотезы, называется альтернатив-
ной гипотезой. Правило, согласно которому проверяют гипотезу H
0
(при-
нимают или отвергают), называется статистическим критерием проверки
гипотезы H
0
. Статистическая гипотеза называется параметрической, если
она представляет из себя предположение о том, что неизвестный параметр
распределения (дисперсия, математическое ожидание и т. п.) имеет наперед
заданное значение или множество значений. В процессе проверки H
0
можно
принять правильное решение или совершить ошибку.
Вероятностью ошибки первого рода называется вероятность откло-
нить H
0
, когда H
0
верна. Эта вероятность совпадает с уровнем значимости
критерия α. Очевидно,
α = P(H
d
= H
1
/H
0
) = P(T (x) ∈ V/H
0
)
(α равняется вероятности того, что значение статистики T принадлежит кри-
тической области V при условии, что верна H
0
).
Вероятностью ошибки второго рода называется вероятность при-
нять H
0
, когда H
0
не верна. Вероятность ошибки второго рода обозначается
β. Очевидно,
β = P(H
d
= H
0
/H
1
) = P(T (x) ∈ V /H
1
)
(β равняется вероятности того, что значение статистики T не принадлежит
критической области V при условии, что верна H
1
).
Величину 1−β будем называть мощностью критерия K и обозначать
M(K). Понятие мощности критерия введено для случая простых H
0
, H
1
; су-
щественно, что множество Θ
1
состоит из единственной точки θ
1
.
Наилучшие критические области (НКО)
Теорема Неймана – Пирсона. Пусть H
0
: θ = θ
0
, H
1
: θ = θ
1
. То-
гда НКО заданного уровня значимости α состоит из точек выборочного про-
странства, удовлетворяющих неравенству
L(x, θ
1
)
L(x, θ
0
)
> c
α
,
63

где c
α
– константа, зависящая от α, L – функция правдоподобия.
Равномерно наиболее мощным (р.н.м.к.) размера α называется ста-
тистический критерий с заданным размером (уровнем значимости) α для
проверки сложной гипотезы H
0
против сложной альтернативы H
1
, мощность
которого не меньше мощности любого другого статистического критерия,
предназначенного для проверки H
0
против H
1
и имеющего тот же размер α.
Критерий K для проверки гипотезы H
0
против простой альтернативы
H
1
называется состоятельным, если
M(K) = P
H
1
(H
d
(X) = H
1
) → 1 при n → ∞.
Критерий размера α, имеющий мощность не меньше α, называется
несмещенным.
Пример 39 (НКО и мощность критерия). Найти НКО и мощность
критерия для проверки гипотезы H
0
: θ = a
0
, против гипотезы
H
1
: a = a
1
, a
1
> a
0
в нормальной модели с известным вторым
параметром σ.
J В модели hN(θ, σ)i рассмотрим функцию правдоподобия
L(x, θ
1
)
L(x, θ
0
)
=
1
(σ
√
2π)
n
e
−
P
n
i=1
(x
i
−a
1
)
2
2σ
2
1
(σ
√
2π)
n
e
−
P
n
i=1
(x
i
−a
0
)
2
2σ
2
= e
−
1
2σ
2
(na
2
1
−na
2
0
−2(a
1
−a
0
)
P
x
i
)
> c
α
.
−
1
2σ
2
(na
2
1
− na
2
0
− 2(a
1
− a
0
)
X
x
i
> ln c
α
.
Выразим член, содержащий статистику (функцию от элементов выборки), и
переобозначим для простоты константу:
−2(a
1
− a
0
)
X
x
i
6 b.
a
1
> a
0
, поэтому
X
x
i
> d
(где d – новая константа). Таким образом, мы нашли статистику
T (x) =
X
x
i
и форму НКО
V = {x :
X
x
i
> d}.
64
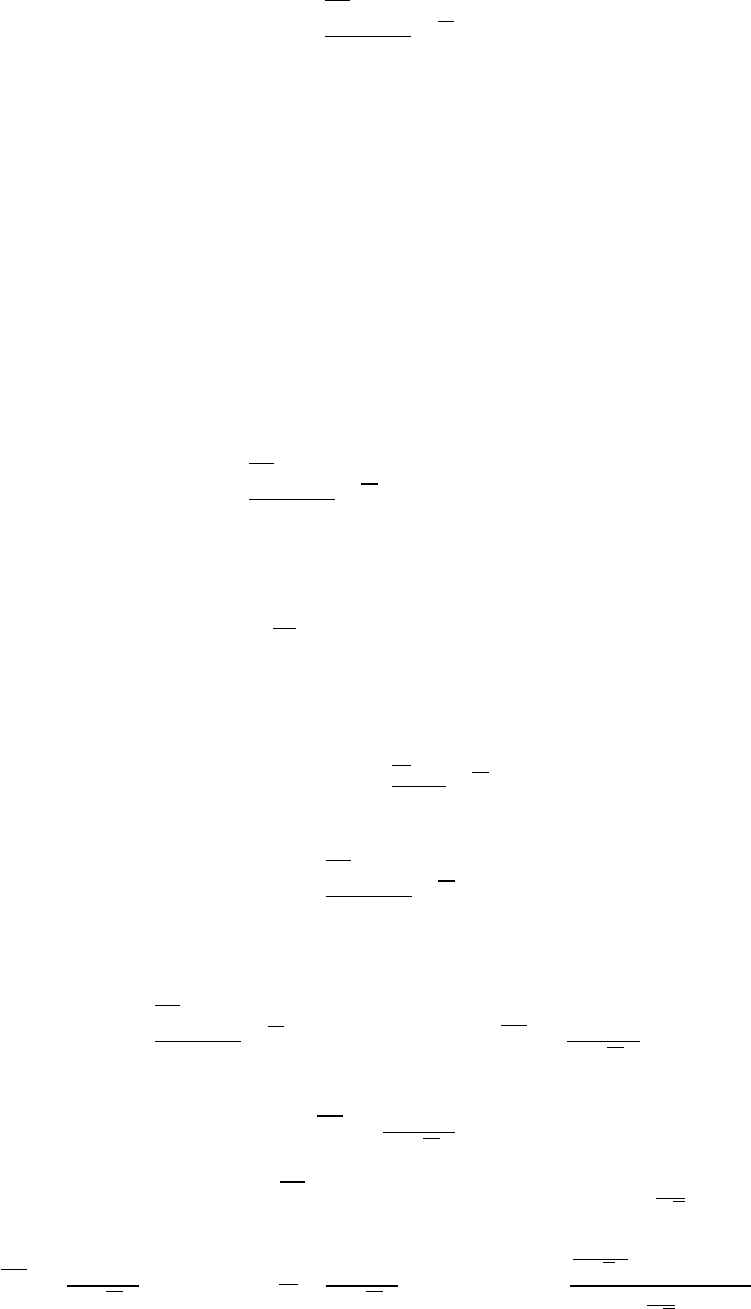
Чтобы найти границу критической области, перейдем к стандартной стати-
стике. Такой статистикой является
Z =
X − a
0
σ
√
n,
доказывали, что Z ∈ N(0, 1). Неравенство
P
x
i
> d равносильно неравен-
ству Z > u, где u – новая константа. Поэтому НКО, заданная через Z, будет
иметь форму
V = {x : Z > u}.
По заданному α из соотношения α = P (Z ∈ V/a
0
) = P (Z > u) найдем u:
P (Z > u) = 1 − F
Z
(u) = 1 −Φ(u) = α,
следовательно,
Φ(u) = 1 −α, u = u
1−α
,
а НКО
X − a
0
σ
√
n > u
1−α
.
Теперь найдем мощность критерия. По определению, мощность критерия
M(K) равна 1 −β, где
β = P (T (x) ∈ V /θ
1
) = 1 −P (T (x) ∈ V/θ
1
).
Тогда
M(K) = P (T (x) ∈ V/θ
1
).
Статистика T (x) в данном случае равна
X−a
0
σ
√
n, θ
1
= a
1
, а критическая об-
ласть V = [u
1−α
, ∞). Таким образом,
M(K) = P
a
1
X − a
0
σ
√
n > u
1−α
.
(P
a
1
означает, что вероятность рассчитывается на основе модели N(a
1
, σ).)
M(K) = P
a
1
X − a
0
σ
√
n > u
1−α
= P
a
1
X >
σu
1−α
√
n
+ a
0
=
= 1 − P
a
1
X <
σu
1−α
√
n
+ a
0
.
Вспомним, что в N(a
1
, σ) X имеет распределение N(a
1
,
σ
√
n
). Тогда
P
a
1
X <
σu
1−α
√
n
+ a
0
= F
X
σu
1−α
√
n
+ a
0
= Φ
σu
1−α
√
n
+ a
0
− a
1
σ
√
n
!
,
65
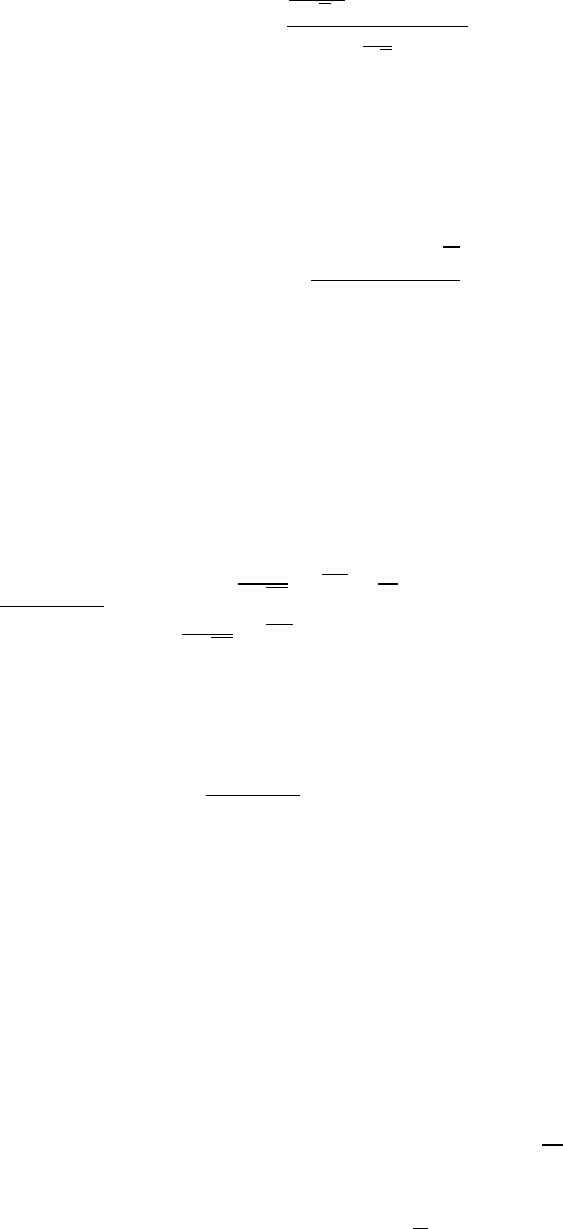
и
M(K) = 1 −Φ
σu
1−α
√
n
+ a
0
− a
1
σ
√
n
!
.
Можно слегка преобразовать последнее выражение, используя свойство
Φ(x):
Φ(−x) = 1 − Φ(x) и свойство квантилей стандартного нормального
распределения: u
α
= −u
1−α
. Окончательно получим
M(K) = Φ
u
α
+
(a
1
− a
0
)
√
n
σ
.
I
Пример 40 (НКО). Найти наилучшую критическую область для про-
верки гипотезы H
0
: R[−a, a] против гипотезы H
1
: N(0, σ) по одному
наблюдению (n = 1) при уровне значимости α = 0, 1.
J
L(x, H
1
)
L(x, H
0
)
=
1
σ
√
2π
e
−
x
2
2σ
2
:
1
2a
, x ∈ [−a, a],
1
σ
√
2π
e
−
x
2
2σ
2
: 0 = ∞, x /∈ [−a, a].
(8)
НКО V заданного уровня значимости α состоит из точек выборочного про-
странства, удовлетворяющих неравенству:
L(x, θ
1
)
L(x, θ
0
)
> c
α
,
следовательно, надо разрешить (8) относительно x. Разрешая, получаем:
V = {x : |x| > a} ∪{x : |x| 6 d},
где d – некоторая константа. Значение константы d найдем из определения
α:
α = P (Z ∈ V/H
0
); P (Z ∈ V/H
0
) = P (|x| 6 d/H
0
)
и, поскольку H
0
: R[−a, a], эта вероятность равна площади прямоугольника
с высотой, равной плотности равномерного распределения
1
2a
, и с основанием
2d. Таким образом,
α = P (|x| 6 d/H
0
) =
d
a
.
Отсюда d = aα, и получен окончательный вид НКО:
V = {x : |x| > a} ∪{x : |x| 6 aα}.
66
Следовательно, если наблюдаемое значение x по модулю больше a, или не
больше aα, гипотеза о равномерном распределении отвергается (в пользу
нормального распределения); если же |x| ∈ (aα; a], гипотеза о равномерном
распределении не отвергается. I
Пример 41 (мощность критерия). В условиях предыдущего примера
найти мощность полученного критерия.
J Мощность критерия численно равна площади над критической областью,
рассчитанной на основе распределения Z при альтернативной гипотезе H
1
.
Решение принимается по одному наблюдению, то есть распределение Z сов-
падает с распределением X. Таким образом, M(K) равна площади криво-
линейной трапеции с основанием V , ограниченной сверху графиком плотно-
сти N(0, σ). Основание трапеции состоит из трех несвязанных интервалов:
(−∞; −a) ∪ [−aα; aα] ∪(a; ∞). Площадь под графиком плотности выража-
ется через функцию распределения, и
M(K) = Φ
0,σ
(−a) + (Φ
0,σ
(aα) − Φ
0,σ
(−aα)) + 1 − Φ
0,σ
(a).
Вспомним, что Φ
0,σ
(x) = Φ(x/σ). Тогда M(K) упрощается и выражается че-
рез функцию Φ(x). При решении задач с числовыми данными подставляются
табличные значения функции Φ(x). I
Задачи
Даны оценки за контрольную работу первой и второй групп X =
(x
1
, . . . , x
n
), Y = (y
1
, . . . , y
m
), которые можно рассматривать как выборки
из генеральных совокупностей оценок. Сформулировать нулевую и альтер-
нативную гипотезы для получения ответа на вопрос:
274. «Учится ли первая группа по этому предмету лучше вто-
рой?»
275. «Одинаково ли успешно учатся по этому предмету первая
и вторая группа?»
276. «Можно ли считать, что первая и вторая группа учатся
по этому предмету одинаково ровно?»
Даны результаты измерений артериального давления у одних и тех же
людей до и после приема лекарства. Сформулировать H
0
и H
1
для получения
ответа на вопрос:
277. «Повышает ли это лекарство давление?»
278. «Понижает ли это лекарство давление?»
67

279. «Это лекарство увеличивает разброс давления у пациен-
тов?»
280. Имеются данные о солнечной активности и о заболевае-
мости дифтеритом за ряд лет. Сформулировать нулевую и альтер-
нативную гипотезы для проверки содержательной гипотезы: «Уве-
личение солнечной активности понижает заболеваемость дифтери-
том».
281. Для каждой из двух книг имеются данные о частотах, с ко-
торыми встречаются в тексте различные служебные слова и знаки
препинания. Сформулировать нулевую и альтернативную гипотезы
для проверки содержательной гипотезы: «Эти две книги написаны
одним автором».
282. Найти наилучшую критическую область в модели N(a, σ)
для проверки гипотезы H
0
: a = a
0
против гипотезы H
1
: a = a
1
по
выборке объема n = 25, если σ = 5, a
0
= 1, a
1
= 3, уровень значимости
α = 0, 05. Найти мощность критерия.
283. В статистической модели f(x) = λe
−λx
, x > 0 найти наилуч-
шую критическую область для проверки гипотезы H
0
: λ = 1 против
гипотезы H
1
: λ = 4 по выборке объема n = 1 при уровне значимости
α = 0, 1. Найти мощность критерия.
284. В статистической модели N(a, σ) найти наилучшую кри-
тическую область для проверки гипотезы H
0
: σ
2
= 4 против ги-
потезы H
1
: σ
2
= 9, если объем выборки n = 25, а уровень значимости
α = 0, 05.
285. Найти наилучшую критическую область для проверки ги-
потезы H
0
: f(x) =
1
2
при |x| 6 1 против гипотезы H
1
: ξ ∈ N(0, 1) по
одному наблюдению (n = 1), α = 0, 05. Найти мощность критерия.
286. Найти наилучшую критическую область для проверки ги-
потезы H
0
: ξ ∈ N(0, 1) против гипотезы H
1
: f(x) =
1
2
при |x| 6 1 по
одному наблюдению (n = 1), если α = 0, 05. Найти мощность крите-
рия.
287. Найти наилучшую критическую область для проверки ги-
потезы H
0
: R[−
1
2
,
1
2
] против гипотезы H
1
: N(0, 0, 16) по одному на-
блюдению n = 1 при уровне значимости α = 0, 1. Найти мощность
критерия.
288. В статистической модели B(N, p) найти наилучшую кри-
тическую область для проверки гипотезы H
0
: p =
1
4
против гипоте-
68

зы H
1
: p =
1
2
, N = 10, если объем выборки n = 25, уровень значимости
α = 0, 1.
289. В статистической модели Γ(α, 1) найти наилучшую крити-
ческую область для проверки гипотезы H
0
: α = 1 против гипотезы
H
1
: α = 3 при n = 16, α = 0, 05.
290. Найти наилучшую критическую область для проверки ги-
потезы H
0
: λ = 1 против гипотезы H
1
: λ = 2 в статистической
модели P
λ
, n = 9, α = 0, 05.
291. Сколько наблюдений необходимо, чтобы мощность крите-
рия для проверки гипотезы H
0
: a = 0 против гипотезы H
1
: a = 2 в
статистической модели была не меньше 0, 9, если уровень значимости
α = 0, 05?
292. Исследовать состоятельность критерия, построенного в
задаче 282.
293. Исследовать несмещенность критерия, построенного в за-
даче 282.
294. Пусть в нормальной модели hN(θ, 1)i по одному наблюдению
проверяется гипотеза H
0
: θ = a
0
= 1, против гипотезы H
1
: θ = a
1
=
4, причем априорные вероятности гипотез равны соответственно
1/4 и 3/4. При каком d полная вероятность ошибки критерия K(x)
будет минимальной?
K(X) =
(
H
1
, X > d,
H
0
, X < d.
69
§ 13. Проверка параметрических
гипотез
Алгоритм проверки статистической гипотезы.
1. Сформулировать статистическую параметрическую модель, нулевую
и альтернативную гипотезы, задать уровень значимости α.
2. Выбрать статистику Z(x), такую, что она сама зависит от параметра
θ, а ее распределение при верной H
0
от θ не зависит и различается при H
0
и
при H
1
.
3. Найти критическую область V .
4. Рассчитать по выборке значение статистики Z
в
.
5. Если Z
в
попадает в критическую область V, то нулевая гипотеза от-
вергается (в пользу альтернативной). Если Z
в
не попадает в критическую об-
ласть V , то нулевая гипотеза не отвергается.
6. Сформулировать ответ в терминах вопроса.
Замечание 1. Гипотеза H
0
отвергается или не отвергается с уровнем
значимости α. Пусть наблюдаемая случайная величина принадлежит классу
нормальных распределений N(θ
1
, θ
2
). Перечислим критерии проверки гипо-
тез о параметрах нормального распределения.
Замечание 2. В данной таблице индекс «0» внизу означает, что значе-
ние параметра известно. Например, N(a, σ
0
) – дисперсия известна (и рав-
на σ
2
0
), а математическое ожидание неизвестно. Индекс «0» вверху означает
предполагаемое значение параметра. Например, a = a
0
– математическое
ожидание неизвестно, и его предполагаемое значение равно a
0
. В последнем
столбце указывается распределение Z при условии, что верна H
0
(Z
/H
0
).
Критерии для проверки гипотез о параметрах одного распре-
деления. Пусть наблюдаемая случайная величина принадлежит классу
нормальных распределений N(θ
1
, θ
2
) ∼ N(a, σ).
Рассмотрим выборку X = {(x
1
, . . . , x
n
)}, элементы которой независи-
мы и имеют распределение N(a, σ).
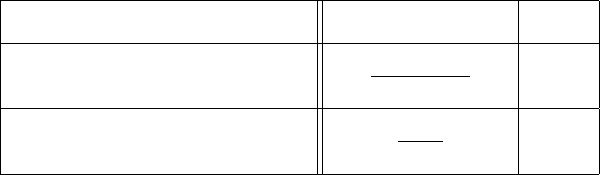
Гипотеза о дисперсии. H
0
: σ = σ
0
.
Статистическая модель Статистика Z Z
/H
0
hN(a
0
, σ)i
P
(x
i
−a
0
)
2
(σ
0
)
2
χ
2
n
hN(a, σ)i
nS
2
(σ
0
)
2
χ
2
n−1
70
