Крупкина Т.В. Математическая статистика. Практикум
Подождите немного. Документ загружается.


144. Найти k, при котором оценка
b
σ
2
= (k
P
n
i=1
|X
i
− a|)
2
являет-
ся несмещенной в N(a, σ).
145. Найти k, при котором оценка
b
σ
2
= k
P
n−1
i=1
(X
i+1
− X
i
)
2
явля-
ется несмещенной в N(a, σ).
146. Найти k, при котором оценка bσ = k|X
1
− X
2
| параметра σ
является несмещенной в N(a, σ), если n = 2.
147. Исследовать на несмещенность оценку ˆα = X
∗
1
, если f(x) =
e
α−x
, x > α.
148. Исследовать на несмещенность оценку параметра a в рас-
пределении Кептейна:
ˆa =
P
n
i=1
g(X
i
)
n
.
149. Исследовать на несмещенность оценку
b
σ
2
=
1
n
P
n
i=1
(g(X
i
) −
a)
2
в распределении Кептейна.
150. Доказать, что в модели логистического распределения
f(x, θ) = e
−x+θ
(1 + e
−x+θ
)
−2
, −∞ < x < ∞
X – несмещенная оценка θ.
151. Предложить три несмещенные оценки параметра a в рас-
пределении N(a, σ).
152. Предложить три различные несмещенные оценки парамет-
ра p биномиального распределения с параметрами N, p.
153. Предложить четыре различные несмещенные оценки пара-
метра λ распределения Пуассона.
154. Исследовать на состоятельность оценку ˆa = X в N (a, σ).
155. Исследовать на состоятельность оценку
b
σ
2
= s
2
в N (a, σ).
156. Исследовать на состоятельность оценку
ˆ
λ = X в распреде-
лении Пуассона P
λ
.
157. Исследовать на состоятельность оценку ˆp =
¯
X
N
в биноми-
альном распределении B(N, p).
158. Исследовать на состоятельность оценку параметрической
функции P
λ
=
λ
k
k!
e
−λ
:
c
P
λ
= I(X
1
= k).
41
159. В модели Бернулли исследовать на несмещенность и состо-
ятельность оценку параметрической функции p(1 − p):
\
p(1 − p) = X
1
(1 − X
2
).
160. Исследовать на состоятельность оценку
ˆ
b = X
∗
n
в R [a, b].
161. Исследовать на состоятельность оценку ˆα = X
∗
1
, если f(x) =
e
α−x
, x > α.
162. Доказать, что если E ˆα = α и Dˆα → 0 при n → ∞, то ˆα –
состоятельная оценка α.
163. Доказать, что если E ˆα → α при n → ∞и D ˆα → 0 при n → ∞,
то ˆα – состоятельная оценка α.
164. Доказать,что если ˆα – состоятельная оценка α, а f –
непрерывная функция, то f(ˆα) – состоятельная оценка f(α).
165. В равномерной модели R[0; θ] оценка параметра θ
ˆ
θ = 2¯x.
Исследовать эту оценку на несмещенность и состоятельность.
42

§ 7. Эффективные оценки
Несмещенная оценка
b
θ параметра θ называется оптимальной оцен-
кой, если D
b
θ 6 D
∼
θ, ∀θ ∈ Θ, где
∼
θ – произвольная несмещенная оценка θ.
Информационным количеством Фишера называется величина I, рав-
ная
I = E
∂ ln f(x
1
, x
2
, . . . , x
n
, θ)
∂θ
2
.
В регулярной модели для дисперсий несмещенных оценок параметра θ
справедливо неравенство Рао – Крамера:
D
ˆ
θ >
1
I
.
В регулярной модели несмещенная оценка
ˆ
θ параметра θ называется
эффективной оценкой θ, если ∀θ ∈ Θ D
ˆ
θ =
1
I
.
Если оценка является эффективной, она оптимальна. Обратное, вооб-
ще говоря, не верно.
Для проверки эффективности оценок удобно использовать следующие
формулы информационного количества Фишера I:
I = n E
∂ ln f(x, θ)
∂θ
2
;
I = −n E
∂
2
ln f(x, θ)
∂θ
2
,
где f(x, θ) – одномерная плотность.
Для дискретной случайной величины вместо f(x) используется P (ξ =
x).
В регулярной статистической модели для несмещенных оценок мож-
но рассматривать показатель эффективности. Показателем эффективно-
сти несмещенной оценки
ˆ
θ параметра θ называется число
e(
ˆ
θ) =
1
ID
ˆ
θ
.
Пример 24. В модели Пуассона P
λ
предлагается следующая оценка
параметра λ :
ˆ
λ =
¯
X. Доказать, что эта оценка эффективна.
J Надо проверить выполнение равенства:
D
ˆ
λ =
1
I
.
43
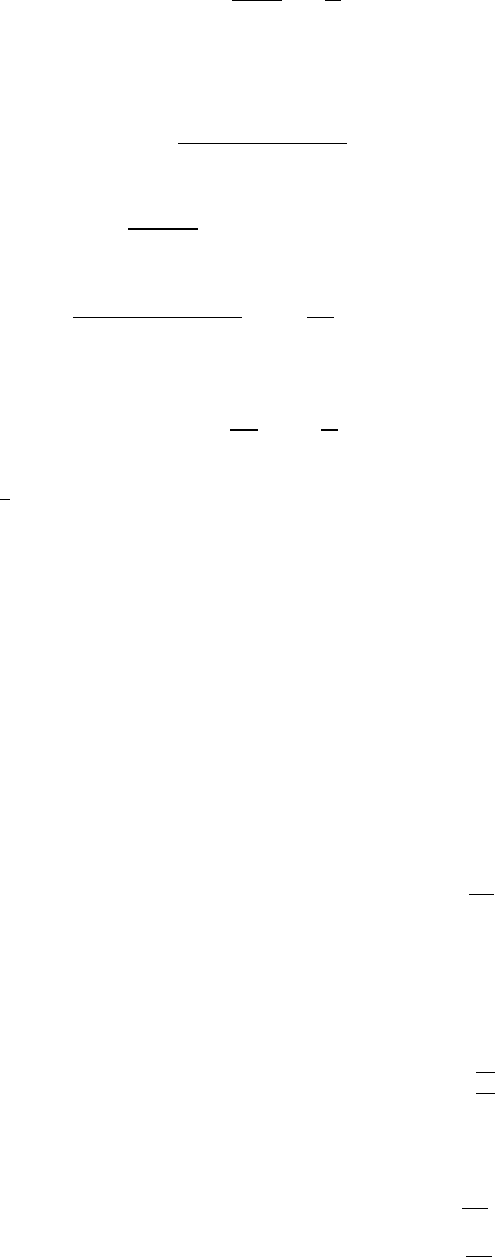
D
ˆ
λ = D
¯
X =
DX
n
=
λ
n
.
Для нахождения информационного количества Фишера I используем фор-
мулу
I = −n E
∂
2
ln P(ξ = x)
∂λ
2
.
Поскольку P(ξ = x) = p
λ
(x) =
λ
x
e
−λ
x!
, то ln P(ξ = x) = x ln λ −λ − ln x! и
∂
2
ln P(ξ = x)
∂λ
2
= −
x
λ
2
.
Тогда
I = −n E
−
x
λ
2
=
n
λ
.
Получили, что D
ˆ
λ =
1
I
, то есть оценка
¯
X является эффективной.I
Пример 25. Исследовать на эффективность оценку параметра α в
распределении с плотностью f(x) = e
α−x
, x > α:
ˆα = X
∗
1
.
J Данная модель не является регулярной, так как выборочное про-
странство X ограничено параметром α. В этой модели эффективных оценок
не существует. I
Задачи
166. Исследовать на эффективность оценку ˆa = X в N (a, σ).
167. Исследовать на эффективность оценку
b
σ
2
= s
2
в N (a, σ).
168. Исследовать на эффективность оценку
ˆ
λ = 1/2(X
1
+ X
2
) в
распределении Пуассона P
λ
.
169. Исследовать на эффективность оценку ˆp =
X
N
в биномиаль-
ном распределении B(N, p).
170. Исследовать на эффективность оценку
ˆ
b = X
∗
n
в R [a, b].
171. Исследовать на оптимальность оценку ˆa =
X в N (a, σ).
172. Исследовать на оптимальность оценку
ˆ
λ = X в распределе-
нии Пуассона P
λ
.
44
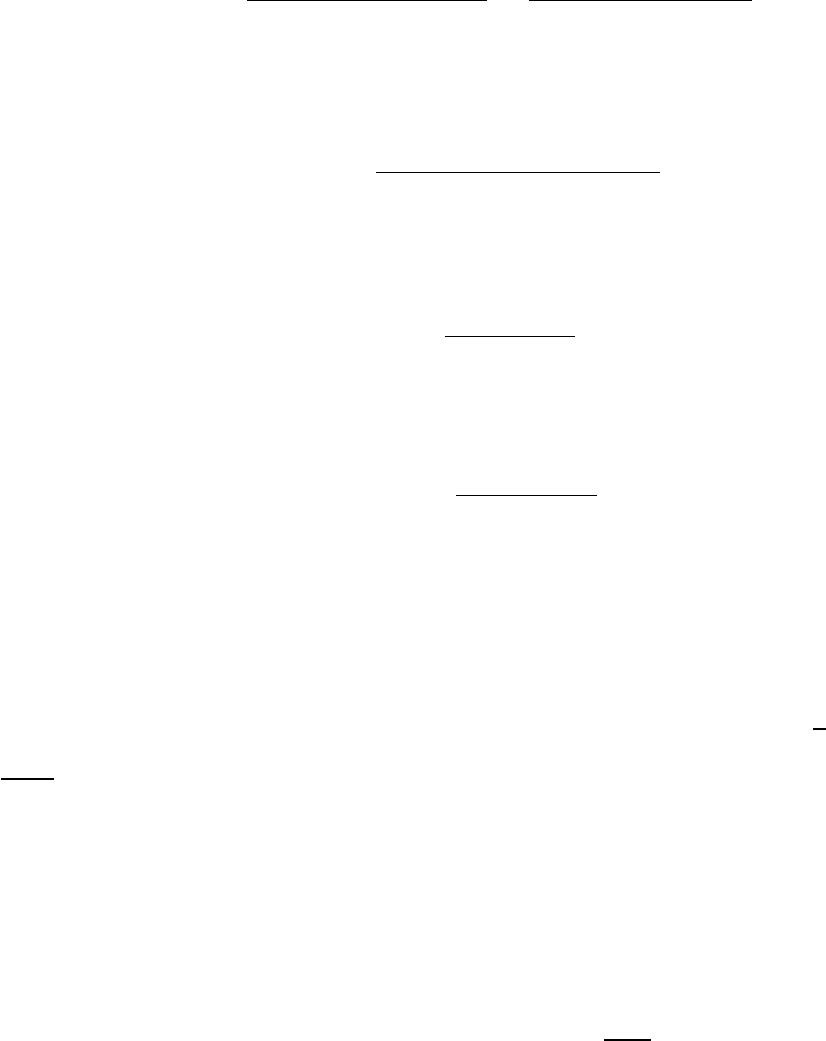
173.
ˆ
λ = X
1
в распределении Пуассона P
λ
. Доказать, что оценка
является несмещенной, но не является эффективной и состоятель-
ной.
174. В распределении с плотностью f(x) = e
α−x
, x > α, оценка
ˆα = X
∗
1
. Найти смещение данной оценки, получить на основе этого
несмещенную оценку и исследовать ее на эффективность.
175. Докажите формулу
I =
+∞
Z
−∞
. . .
+∞
Z
−∞
∂f(x
1
, x
2
, . . . , x
n
, θ)
∂θ
2
1
f(x
1
, x
2
, . . . , x
n
, θ)
dx
1
. . . dx
n
.
176. Докажите формулу
I = −E
∂
2
ln f(x
1
, x
2
, . . . , x
n
, θ)
∂θ
2
.
177. Докажите формулу
I = n E
∂ ln f(x, θ)
∂θ
2
.
178. Докажите формулу
I = −n E
∂
2
ln f(x, θ)
∂θ
2
.
179. Докажите, что показатель эффективности e удовлетво-
ряет неравенству 0 < e(
ˆ
θ) 6 1, а для эффективных оценок e(
ˆ
θ) = 1.
180. Пусть T
1
– эффективная оценка параметра α, а T
2
– несме-
щенная оценка параметра α. Доказать, что ρ(T
1
, T
2
) =
√
e, где e =
1
I·DT
2
– показатель эффективности T
2
.
Указание. Рассмотреть оценку T = (1 − k)T
1
+ kT
2
.
181. В равномерной модели R[0; θ] оценка параметра θ
ˆ
θ = 2¯x.
Исследовать эту оценку на оптимальность.
182. Докажите, что в неравенстве Рао – Крамера равенство до-
стигается тогда и только тогда, когда
ˆ
θ и
∂ ln f
∂θ
линейно зависимы.
45

§ 8. Методы нахождения оценок
Метод максимального правдоподобия. Для непрерывной случай-
ной величины функция
L(x
1
, . . . , x
n
, θ) = f(x
1
, θ) · . . . · f(x
n
, θ),
рассматриваемая при фиксированных (x
1
, . . . , x
n
) как функция параметра θ,
называется функцией правдоподобия.
Функция правдоподобия для дискретной случайной величины опреде-
ляется в виде
L(x
1
, . . . , x
n
, θ) = P(ξ = x
1
) · . . . ·P(ξ = x
n
).
Оценка θ
∗
, обеспечивающая по параметру θ максимум функции прав-
доподобия, называется оценкой максимального правдоподобия парамет-
ра θ (о.м.п.).
Вместо отыскания максимума функции L часто удобнее находить мак-
симум функции ln L и решать уравнение правдоподобия
∂ ln L
∂θ
= 0.
В результате решения уравнения правдоподобия мы найдем критическую
точку, необходимо еще убедиться, что это точка максимума.
Метод моментов. Приравнивая выборочные и теоретические момен-
ты, получаем уравнения относительно θ. Решая эти уравнения, получаем
оценку параметра
ˆ
θ. Эта оценка называется оценкой метода моментов и
обозначается о.м.м.
Пример 26. Найдем о.м.п. параметра распределения Пуассона.
J
L =
n
Y
i=1
P
λ
(x
i
) =
e
−λn
λ
P
x
i
Q
(x
i
!)
.
ln L(X, λ) = −λn +
X
x
i
lnλ − ln
Y
(x
i
!).
Найдем max ln L(X, λ).
∂ ln L(X, λ)
∂λ
= −n +
P
x
i
λ
= 0.
Получаем
ˆ
λ =
P
xi
n
= ¯x. Очевидно, это точка максимума, так как
∂
2
ln L
∂λ
2
< 0 =⇒ ¯x – о.м.п. λ. I
46

Пример 27. Найдем в условиях предыдущего примера оценку макси-
мального правдоподобия функции параметра λ
2
.
J По свойству инвариантности
b
λ
2
= (
b
λ)
2
= (¯x)
2
. I
Рассмотрим нахождение оценки параметра методом максимального
правдоподобия в нерегулярной модели.
Пример 28. Найдем о.м.п. параметра θ = (a, b) в распределении R[a, b].
J
L =
n
Y
i=1
f(x
i
) =
n
Y
i=1
1
b − a
=
1
(b − a)
n
.
Частная производная
∂ ln L
∂θ
не обращается в 0. Но функция L монотонна по
a и b. Поэтому она достигает своего наибольшего значения при минималь-
ном значении b и максимальном значении a. Но минимальное возможное
значение b ограничено максимальным элементом выборки, а максимальное
возможное значение a ограничено миниимальным элементом. Таким обра-
зом, оценками максимального правдоподобия будут служить минимальный
и максимальный элементы выборки:
ˆa = y
min
= x
∗
1
,
ˆ
b = x
max
= x
∗
n
. I
Пример 29. Найти методом моментов оценки параметров распреде-
ления Γ
α, β
.
J
E ξ =
β
α
, Dξ =
β
α
2
.
β = α E ξ =⇒ Dξ =
E ξ
α
Тогда
α =
E ξ
Dξ
, β =
(E ξ)
2
Dξ
.
Мы получили оценки
ˆα =
X
S
2
,
ˆ
β =
¯x
2
S
2
. I
Пример 30. Найти методом моментов оценки параметров распреде-
ления R[a, b].
47

J
E ξ =
a + b
2
, Dξ =
(b − a)
2
12
,
a = 2 E ξ − b =⇒ Dξ =
(b − E ξ)
2
3
.
Отсюда b = E ξ + σ
√
3, a = E ξ − σ
√
3. Окончательно
ˆa = X − s
√
3,
ˆ
b = X + s
√
3. I
Задачи
183. Найти оценки максимального правдоподобия параметров
a, σ в N(a, σ).
184. Доказать свойство инвариантности о.м.п.: если оцени-
вается некоторая взаимно однозначная параметрическая функция
τ(θ), то ее о.м.п.
d
τ(θ) = τ (
b
θ).
185. Найти оценку максимального правдоподобия функции a
2
+a
в N(a, σ).
186. Найти оценку максимального правдоподобия параметра p в
B(N, p).
187. Найти оценку максимального правдоподобия функции
P
3
i=0
p
i
в B(N, p).
188. Найти оценку максимального правдоподобия функции
√
λ +
λ в P
λ
.
189. Найти оценку максимального правдоподобия параметра
(a, b) в R[a, b].
190. Найти оценку максимального правдоподобия параметра α,
если f(x) = e
α−x
, x > α.
191. Найти оценку максимального правдоподобия параметра α,
если f(x) =
e
−|x|
2(1−e
−α
)
, |x| 6 α.
192. Найти оценку максимального правдоподобия параметра θ
по выборке (x
1
, . . . , x
n
), если
f(x) =
2x
θ
e
−
x
2
θ
, θ > 0, x > 0.
48

193. Найти оценку максимального правдоподобия параметра α
в Γ(α, 2).
194. Найти оценку максимального правдоподобия параметра a в
N(a,
√
2a). Исследовать полученную оценку на состоятельность.
195. Найти методом моментов оценки параметров a, σ в N(a, σ).
196. Найти методом моментов оценку параметра λ в P
λ
.
197. Найти методом моментов оценку параметра λ в распреде-
лении с плотностью f(x) = λe
−λx
, x > 0.
198. Найти методом моментов оценку функции 1/α в показа-
тельном распределении с параметром α.
199. Найти методом моментов оценку параметра λ в P
λ
по вто-
рому моменту.
200. Найти методом моментов оценку параметра b в R[0, b], ис-
пользуя второй момент.
201. Найти методом моментов оценки параметров распределе-
ния R[a, b], используя начальные моменты.
202. Найти методом моментов оценку параметра p в B(N, p)
при известном N.
203. Найти методом моментов оценки параметров N, p в
B(N, p).
204. Доказать состоятельность оценок метода моментов.
205. Найти методом моментов оценку параметра n в χ
2
n
. (χ
2
n
=
P
n
i=1
ξ
2
i
, ξ
i
∈ N(0, 1), ξ
i
независимы.)
206. Найти оценки максимального правдоподобия параметров
a, σ в распределении Кептейна.
207. Найти оценки максимального правдоподобия параметров
α, µ, если f(x) =
1
2α
e
−|x−µ|
α
.
208. Величина ψ имеет бета-распределение с параметрами α и β.
Математическое ожидание и дисперсия бета-распределения извест-
ны:
E ψ =
α
α + β
, Dψ =
αβ
(α + β)
2
(α + β + 1)
.
Найти методом моментов оценки параметров α и β.
49
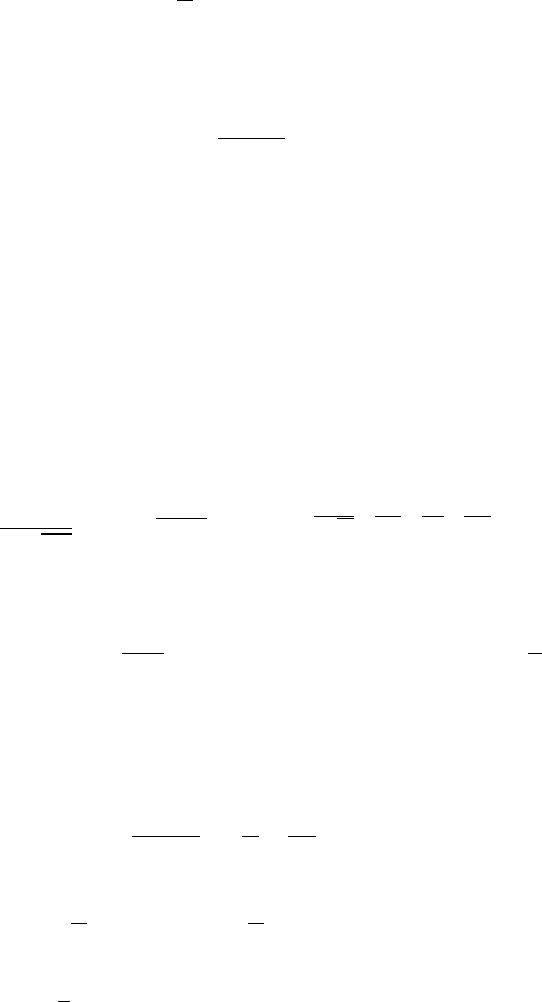
§ 9. Экспоненциальное семейство
Говорят, что распределение с плотностью f(x) принадлежит экспонен-
циальному семейству, если f(x) представима в виде
f(x) = e
A(x)·B(θ)+C(x)+D(θ)
,
Теорема 8. Для того чтобы в модели существовала эффективная
оценка, необходимо и достаточно, чтобы модель принадлежала экс-
поненциальному семейству. При этом эффективной оценкой являет-
ся статистика
T (x) =
1
n
n
X
i=1
A(x
i
),
и она оценивает параметрическую функцию
τ(θ) = −
D
0
(θ)
B
0
(θ)
.
В случае многомерного параметра θ = (θ
1
, . . . , θ
k
) и непрерывной па-
раметрической модели говорят, что распределение с плотностью f(x) при-
надлежит экспоненциальному семейству, если f(x) представима в виде
f(x) = e
P
k
i=1
A
i
(x)·B
i
(θ)+C(x)+D(θ)
.
Пример 31. Докажем, что N(0, σ) принадлежит экспоненциальному
семейству, и найдем эффективную оценку параметра σ.
J
f(x) =
1
σ
√
2π
· exp
−
(x−a)
2
2σ
2
= exp
ln
1
σ
√
2π
−
x
2
2σ
2
+
x·a
σ
2
−
a
2
2σ
2
Параметром является σ, тогда
A(x) = (x −a)
2
, B(σ) = −
1
2σ
2
, C(x) = 0, D(σ) = −ln σ −
1
2
ln 2π.
Следовательно, распределение N(a, θ) принадлежит экспоненциальному се-
мейству. Найдем эффективную оценку параметрической функции от пара-
метра θ = σ :
τ(σ) = −
D
0
(a)
B
0
(a)
=
1
σ
:
1
σ
3
= σ
2
T (x) =
1
n
n
X
i=1
A(x
i
) =
1
n
n
X
i=1
(x
i
− a)
2
.
По теореме 8 оценка
b
σ
2
=
1
n
P
n
i=1
(x
i
− a)
2
эффективна. I
50
