Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
199
222
2
1
2
(,) exp sin
k
k
ka kx
uxt a t
eee
ππ
∞
=
⎧⎫
=−
⎨⎬
⎩⎭
∑
(4.68.а)
или его простейшую аналитическую аппроксимацию в виде:
22
1
2
2
(,) exp sin .
aax
uxt t
eee
π
π
⎧⎫
≈−
⎨⎬
⎩⎭
(4.68.б)
Синтез управлений основан на формулировке одноточечных
или многоточечных целевых условий типа равенств (4.64), нера-
венств (4.65), а также целевых условий в виде минимума функ-
ционалов (4.66), определенных на решениях (4.67) или (4.68):
).t,x(u
e
x
sint
e
a
exp
e
a2
)t,x(u
i
зад
ii
2
22
1
=
⎭
⎬
⎫
⎩
⎨
⎧
−≈
ππ
22
1
2
2
(,) exp sin (,).
зад
xx
tt
aax
uxt t u xt
eee
ππ
=
=
⎧⎫
=− =
⎨⎬
⎩⎭
Для одноточечного условия (4.64) по времени и координатам
задача сводится к решению равенств относительно параметров
j
a
:
(,) (,)
ij зад ij
uxt u xt
=
(4.69)
Равенство (4.69) – это алгебраическое уравнение относитель-
но параметров, которые обеспечивают выполнение целевых усло-
вий. В случае «многоточечных» целевых условий (4.69), задаю-
щих тепловые режимы объекта на семействах точек временной и
координатной осях, можно свести задачу к решению системы от-
носительно параметров. Для ряда с конечным числом слагаемых
задача преобразуется к системе алгебраических уравнений:
).t,x(u
e
xk
sint
e
ak
expa
e
2
)t,x(u
jiijзад
i
j
2
222
kji
=
⎭
⎬
⎫
⎩
⎨
⎧
−=
∑
π
π
(4.70)

200
где суммирование проводится по множествам
x
Di
∈
,
T
Dj ∈
, при-
чем эти множества определяют области задания целевых условий.
Задача 2. Для синтеза управлений для процесса с уравнени-
ем теплопроводности, начальными и граничными условиями:
,0|),(),,(|),(,
0
2
==Δ=
= ГУНУtt
yxuyxuyxuuau
и начально-краевой задачей, можно использовать решение в виде
ряда:
1
22
22
22
0
4
(, ,) exp sin ,
kj
kj
m
k
j
kx
uxyt a a t
eeme
π
π
∞
==
⎧⎫
⎛⎞
=−+
⎨⎬
⎜⎟
⎝⎠
⎩⎭
∑
(4.71)
если S – прямоугольник с определенными выше параметрами.
Многоточечные целевые условия типа равенства представ-
ляются системой уравнений вида:
).t,y,x(u
e
xk
sint
m
j
e
k
aexpa
e
4
)t,y,x(u
vwiзад
2
2
2
2
22
0jk
kj
m
vwi
1
=
⎭
⎬
⎫
⎩
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=
∑
∞
==
π
π
(4.72)
Для реализации можно использовать ограниченное число
слагаемых в сумме равенства (4.72), где параметры
i
,
w
,
v
, оп-
ределяют конечное дискретное множество точек области, в кото-
рой заданы целевые условия. Соотношение типа (4.72) представ-
ляет собой систему алгебраических уравнений относительно па-
раметров
kj
a
. Аналогично формулируются многоточечные целе-
вые условия типа (4.65) в виде двусторонних неравенств:
(4.73)
которые являются линейными алгебраическими неравенствами
),t,y,x(u
e
xk
sint
m
j
e
k
aexpa
e
4
)t,y,x(u
vwi
2
2
2
2
22
0jk
kj
m
vwi
1
+
∞
==
−
≤
⎭
⎬
⎫
⎩
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−≤
∑
π
π
4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
201
относительно параметров
kj
a
. Множества, содержащие параметры
задачи
i
,
w
,
v
, имеют тот же смысл, что и в (4.72). Рассмотрен-
ная процедура синтеза на основе решения начально-краевых задач
является двухэтапной. На первом этапе определяются коэффици-
енты
kj
a
, а на втором – функции начального нагрева u
0
(x,y), по-
скольку
kj
a
=
0
((,))
kj
aux
y
.
Задача 3. Трехмерная краевая задача теплопроводности:
(4.74)
имеет аналитическое решение в виде сумм специальных функций:
2
2
(1/2)
2
2
00
(2 1)( )!
1
(,) exp *
(1 )( )!
e
ijm j
ijme
om
eem
a
uxt a t
Rem
Rr
μ
δ
π
∞∞ ∞
+
===−
+−
⎧⎫
⎡⎤
=−
⎨⎬
⎣⎦
++
⎩⎭
∑∑∑
(4.75)
где
J
– специальная функция Бесселя, при этом
S
– кольцо.
Целевые условия типа равенств или неравенств формулиру-
ются аналогично, однако усложненная структура решений приво-
дит к возрастанию сложности процедуры синтеза. Если модель
(4.75) использовать совместно с условием типа равенств-
неравенств, то в результате синтеза вычисляются коэффициенты
ijm
a
, что завершает первый этап синтеза.
На основе развиваемого подхода можно сформулировать
стационарную задачу распределения тепла в стержне, когда вы-
числения на первом и втором этапах менее трудоемкие.
Задача 4. Пусть имеется задача Дирихле вида:
(4.76)
,0),,,(,
0
2
==Δ=
= sott
uzyxuuuau
[]
),,(Y)
R
r
(J
)(J
1
*
m
j
)2/1i(
j2/1i
2)2/1i(
2/1i
ϕΘμ
μ
+
+
+
+
.)(,)(,0,0
000
xuuxuuuuu
eeyyaxx
=====Δ
====

202
Задача соответствует ситуации задания распределения тем-
ператур на двух краях стержня. Для синтеза можно воспользо-
ваться описанной выше методикой при задании целевых условий
типа равенств (4.64). В результате можно получить систему алгеб-
раических уравнений относительно искомых параметров:
(4.77)
Поскольку (4.77) является системой линейных алгебраических
уравнений, то на первом этапе синтеза определяются неизвестные
параметры задачи. На втором этапе по вычисленным параметрам
определяются функции «начального нагрева»:
(4.78)
Соотношения (4.78), где
,
kk
ab
определены на первом этапе
задачи, являются функциями
0
()ux
. Решение последних уравнений
относительно искомых функций возможно также на основе ее
представления в виде линейной комбинации с неизвестными па-
раметрами в классе выбранных базисных функций. В результате
задача сводится к определению параметров линейной комбина-
ции. Рассмотренные результаты допускают распространение для
других целевых условий – условий типа (4.65) или (4.66), что при-
водит к задачам математич
еского программирования.
Задача 5. Требуется определить функцию начального нагре-
ва тонкого бесконечного стержня для обеспечения в момент вре-
мени t = 0.3 в точке
x
= 0.5 температуру величиной 0.164.
Для решения задачи воспользуемся «одноточечными» целе-
выми условиями, определим из соотношения (4.69) коэффициент
,adx
a
xk
sin)x(ua
e
0
kok
∫
==
π
.bdx
a
xk
sin)x(ub
e
0
kek
∫
==
π
.)y,x(u
a
k
h
xksin
)
a
yk
shb
a
ye
shka(
a
2
)y,x(u
1k
nn
зад
e
vw
k
v
k
∑
∞
=
=+
−
=
π
δ
ππ
π

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
203
1
a
и синтезируем функцию начального нагрева
()yx
. Далее с по-
мощью соотношения (4.68-б) проверяется обеспечение заданной
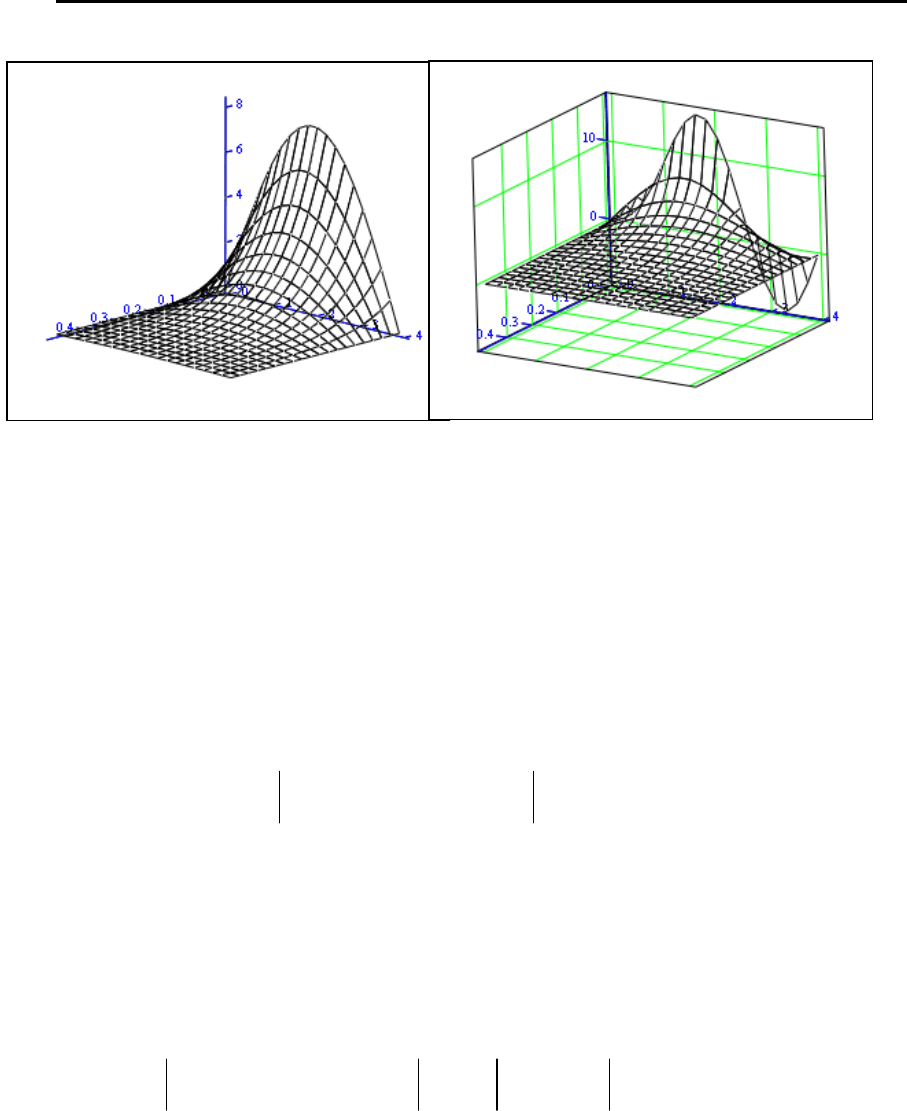
температуры в заданной точке. Результаты приведены на рис 4.4.
Задача 6. Рассматривается синтез с «трехточечными» целе-
выми условиями для обеспечения заданных значений температуры
в трех точках стержня в заданные моменты времени. Сначала оп-
ределяются амплитуды гармоник функции начального нагрева на
основе (4.70), затем - функция теплового нагрева (рис. 4.5).
Таким образом, синтез программных управлений на основе
аналитических решений имеет ограничения на применение.
4.8.5. Синтез локально-оптимальных управлений. Ло-
кально-оптимальные программные (программно-замкнутые)
управления синтезируются как программные (программно-
замкнутые) управления на основе прогнозирования динамики теп-
ловых процессов с помощью классических разностных схем.
Для объектов, описываемых одномерными уравнениями теп-
лопроводности
(4.79.а)
с начальными и краевыми условиями вида:
(4.79.б)
В последних уравнениях заданы краевые условия, соответствую-
щие случаям бесконечного и конечного (с единичной длиной) од-
номерного стержня.
Для синтеза управлений можно сформул
ировать различные
типы функционалов, соответствующих локально-оптимальным
требованиям. Эти требования можно представить несколькими
,
2
fuau
xxt
+=
),x(u)x,0t(u
0
==
;0),0(u
=
−
∞
,0),0(u
=
+
∞
.u)l,0(u
,u)0,0(u
l0
00
=
=
204
Рис. 4.4. Распределение Рис. 4.5. Распределение температуры
температуры на основе на основе «трехточечных»
«одноточечных» целевых условий
целевых условий
функционалами. Первый функционал качества, имеющий вид:
(4.80)
q
= 1, 2, характеризует мгновенную ошибку отклонения от задан-
ной температуры, являясь степенной функцией модуля разности
между текущим и заданным значением температуры.
Второй
функционал
,
0>
ρ
, (4.81)
также описывает погрешность поддержания температуры и оце-
нивает отклонения от экономически оптимального управления в
виде распределенного воздействия, описываемого функцией
(,)
f
xt
. Функционалы типа (4.80) и (4.81), характеризующие мгно-
венные погрешности и мгновенные затраты, являются локальны-
min,)x,t(u)x,t(uJ
q
зад
→−=
q
эк
q
зад
2
ff)x,t(u)x,t(uJ −+−=
ρ
G

4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
205
ми. Третий функционал
,
0>
ρ
, (4.82)
является суммарным функционалом, учитывающим ошибки по
времени и координате при программировании изменения темпера-
туры как функции времени и координаты на интервале
[, ]ii k+
:
).x,t(uα)x,t(u
kii
+
=
(4.83)
Уравнение (4.83) задает технологические требования.
Математические формулировки задач вычисления управ-
лений.
Для рассматриваемых классов функционалов можно сфор-
мулировать различные законы программирования и стабилизации.
Эти закоы можно выбрать априорно на основе некоторых рассуж-
дений. Далее будет рассмотрен вариант синтеза, когда тип закона
формируется естественным образом на основе заданного функ-
ционала, используемой модели процесса нагревания и ограниче-
ний по области нагрева или охлаждения. Очевидно, что закон
должен быть функцией времени и коорд
инат и должен формиро-
ваться с использованием прогнозирования по пространству и вре-
мени, что обобщает на случай распределенных объектов методику
синтеза, рассмотренную в п. 4.7. Данная методика позволяет ис-
пользовать целевые условия, сформулированные не только в виде
минимизации функционалов, а при синтезе также могут быть уч-
тены заданные соотношения между координатам
и на различных
«срезах» пространства и времени. Формирование управлений на
основе оптимизации процессов на многообразиях, когда требова-
ния к качеству формализуются заданием линейных многообразий.
Алгоритм синтеза имеет вид:
Этап 1: формулировка классической разностной схемы для
уравнения теплопроводности (4.79.а):
∑
⎥
⎦
⎤
⎢
⎣
⎡
−+−=
ij
q
ji
эк
ji
q
ji
зад
ji
xtfxtfxtuxtuJ ),(),(),(),(
3
ρ
206
,f
h
uu2u
a
uu
:
0x
1t
0,1
2
1,10,11,1
2
0,10,2
+
+
−
=
−
=
=
−
τ
,f
h
uu2u
a
uu
:1x
1,1
2
0,11,12,1
2
1,11,2
+
+
−
=
−
=
τ
.f
h
uu2u
a
uu
:2x
2,1
2
1,12,13,1
2
2,12,2
+
+
−
=
−
=
τ
,f
h
uu2u
a
uu
:
0х
0t
0,0
2
1,00,01,0
2
0,00,1
+
+
−
=
−
=
=
−
τ
,f
h
uu2u
a
uu
:
1x
0t
1,0
2
0,01,02,0
2
1,01,1
+
+
−
=
−
=
=
τ
,f
h
uu2u
a
uu
:
2x
0t
2,0
2
1,02,03,0
2
2,02,1
+
+
−
=
−
=
=
τ
1, , , 1 , , 1
2
,
2
2
,
t x tx tx tx tx
tx
uu u uu
af
h
τ
++−
−−+
=+
(4.84)
где сеточные аргументы по времени и по пространству задаются
индексами внизу, разделенными запятыми так, что соответствие
между непрерывными и дискретными аргументами определяется
соотношениями:
xt
uxtu
,
),( →
.
Этап 2: целевое условие (4.82) в классе моделей (4.84) пре-
образуется в соответствии с введенными обозначениями сеточных
переменных. Тогда минимизируемый функционал
,
0>
ρ
, (4.85)
учитывает отклонения температуры и управлений от заданий.
Этап 3: формулиовка модели динамики по пространству и
времени в виде разностных схем (4.84) для описания процессов
для заданных моментов времени и координат:
(4.86)
Соотношения (4.86) определяют
динамику пространствен-
но-временного изменения температуры
, а также ограничения
q
эк
xtxt
q
зад
xtxt
ffuuJ
,,,,2
−+−=
ρ
4. МЕТОДЫ СИНТЕЗА ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
20
7
задачи математического программирования, в которой перемен-
ными являются значения температуры как функции дискретного
времени и пространственных переменных:
1,0 2,0 0,1
, , ...uuu
Известно, что решение большинства стационарных или не-
стационарных линейных краевых задач сводится к решению ли-
нейных алгебраических систем высокой размерности со слабо за-
полненными матрицами специальной структуры. Для локальной
оптимизации на основе модели (4.86) можно сформулировать
функционал:
(4.87)
где дискретные временной аргумент и координатные аргументы
принадлежат заданным множествам. В функционале (4.87) заданы
требования к точности поддержания температурн
ого режима (пер-
вое слагаемое) и условия экономичности обеспечения (второе сла-
гаемое). При этом смысл воздействия
,tx
f
определен выше. Соот-
ношения (4.86) и (4.87) могут использоваться как для программно-
го синтеза как основы синтеза систем стабилизации. На основании
«суженной» задачи формулируются законы стабилизации в виде
воздействия
,
x
t
f
.
Этап 4: в результате синтеза класс законов стабилизации
формулируется естественным образом как задача минимизации
функционала (4.87) на пересечении непустого линейного много-
образия
0
{|
,,
}
mn m
D
xAx b A R b R
×
==∈ ∈
, (4.88)
где матрица
A
и вектор
b
определяются условиями типа (4.86), а
интервальные ограничения – параллелепипедом конечномерного
пространства:
3, , , ,
,, ,
q
зад эк зад зад
tx tx tx tx t x
Ju u f f tN xN
ρ
=− + − ∈ ∈

208
(
)
.
1
+−
≤≤= zzzzD
(4.89)
В результате решение задачи синтеза может быть получено чис-
ленными методами. Вычисление оптимальных управлений явля-
ются частью общей проблемы синтеза. Важной составляющей
проблемы является аналитическое описание управляющего уст-
ройства, что необходимо для анализа устойчивости замкнутой
системы. В этой связи весьма важно использовать численно-
аналитические методы решения экстремальных задач стабилиза-
ции. Один из подходов ч
исленно-аналитического решения может
быть основан на применении операторов оптимизации, рассмот-
ренных в приложении.
Операторы конечномерной оптимизации в численно-
аналитической форме определяют решение экстремальных задач
минимизации функционалов на пересечении линейного многооб-
разия типа (4.88) (определяющем многошаговую модель теплово-
го процесса по времени и пространству) с учетом технологических
ограничений типа двухсторонних неравенств, и тем самым задать
закон управления на основе приведенных соотношений. «Алгеб-
раизация» задачи синтеза позволяет определить класс управ
лений,
которые могут использоваться как программные управления или в
качестве программно-замкнутых управлений, являющихся анало-
гами управлений, рассмотренных в п. 4.7.
