Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

011
1*
з
)1()1()( aaaajA
m
m
m
m
+−⋅⋅⋅+−+−=π
−
−
.
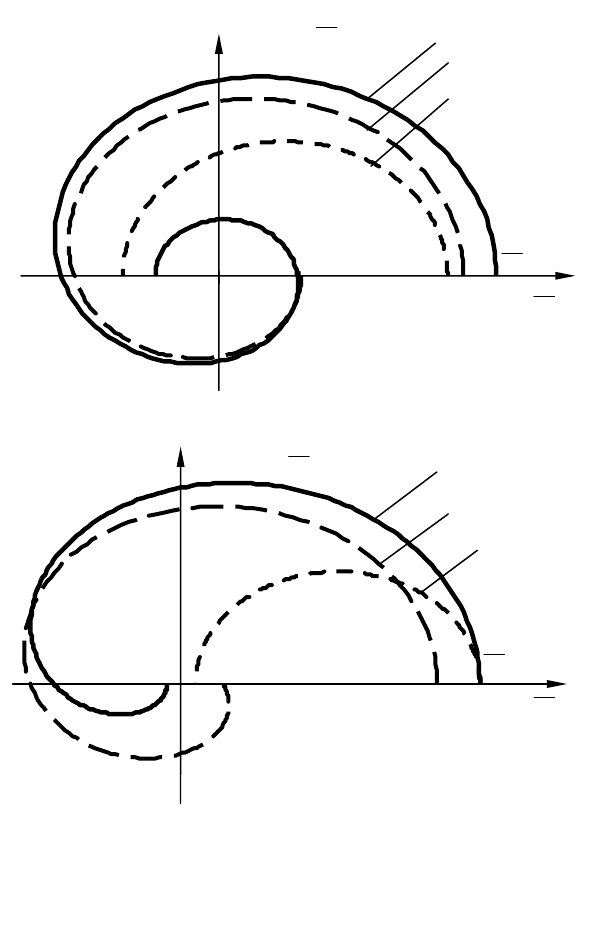
В этом случае нетрудно видеть (см. рис 10.5, а), что необходи-
мыми условиями являются
0)0(
*
з
>A , 0)(
*
з
<πjA (10.13)
для нечетных
m и
0)0(
*
з
>A , 0)(
*
з
>πjA (10.14)
)(Im
*
з
ωjA 3
=
m
2
=
m
1
=
m
0 0=
ω
)(Re
*
з
ωjA
a
)(Im
*
з
ωjA 3
=
m
2
=
m
1
=
m
0
0
=
ω
)(Re
*
з
ωjA
б
Рис. 10.5. Характеристические кривые для
устойчивых (а) и неустойчивых (б)
САУ
р
азличного по
р
ядка
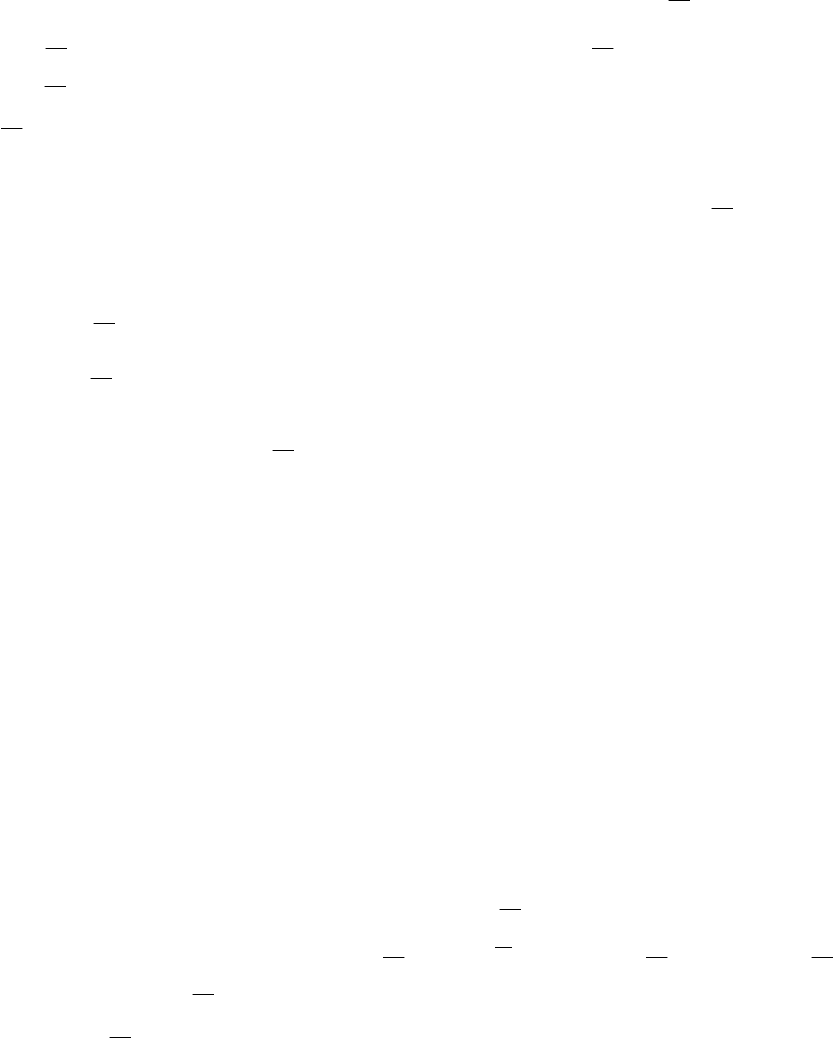
для четных m . Поэтому перед применением данного критерия нужно
проверить выполнение условий (10.13) и (10.14).
Аналог критерия Михайлова можно также сформулировать по-
другому (доказательство этого приведено в [11]). Замкнутая систе-
ма с АИМ будет устойчива, если вещественная
)(
*
з
ωU и мнимая
)(
*
з
ωV характеристической кривой )(
*
з
ωjA в интервале
π≤ω≤0 имеют m вещественных перемежающихся нулей и при
0=ω )0(
*
з
U и )0(
*
з
V имеют одинаковые знаки.
Граница устойчивости системы определяется совокупностью
параметров, при которых характеристическая кривая
)(
*
з
ωjA прохо-
дит через начало координат, т.е. на границе устойчивости
=ω
=ω
.0)(
,0)(
*
з
*
з
V
U
(10.15)
Значение частоты
ω , при котором выполняется система уравне-
ний (10.15), определяет граничную частоту.
Пример 10.2. С помощью аналога критерия Михайлова опреде-
лить устойчивость и найти граничный коэффициент передачи для
САУ, приведенной на рис. 9.8, при следующих ее параметрах:
25
и
=k , 2,0=
β
, 5,0=
γ
.
Характеристический полином системы, приведенной на рис. 9.8,
имеет вид
01и
*
з
)]1(1[)( aeaekeeqA
qq
+=−−−=
βγ
β
−
,
где
1
1
=a , 334,1)]1(1[
и0
=−−−=
βγ
β−
ekea .
Произведем замену оператора
q на
ω
j
и построим на комплекс-
ной плоскости кривую
ω++ω=+=ω
ω
sincos)(
001
*
з
jaaeajA
j
при изменении
ω от 0 до
π
. Система неустойчива, поскольку кри-
вая
)(
*
з
ωjA располагается только в первом квадранте комплексной
плоскости (рис.10.6) .
Неустойчивость САУ подтверждается также не выполнением усло-
вий (10.14). Действительно, при
25
и
=
k
0334,2)0(
*
з
>=A , а
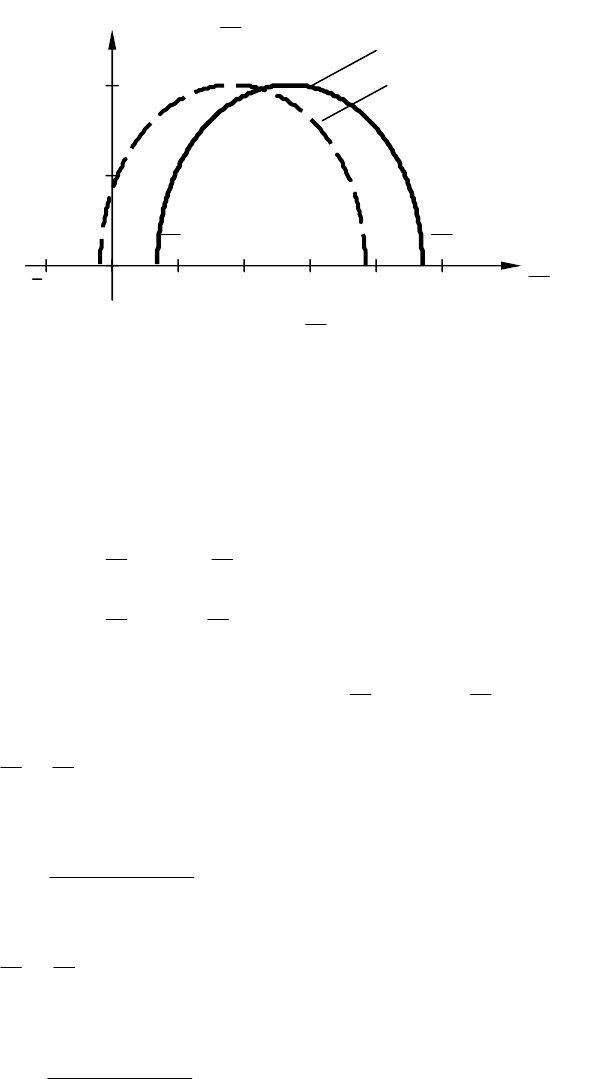
0334,0)(
*
з
>=πA
, следовательно, не выполнено второе условие в
(10.14) и система неустойчива.
На основании системы уравнений (10.15) найдем граничное
значение коэффициента передачи
гри,
k
ω=ω
=−−−ω=ω
βγβ−
.sin)(
,0)]1(1[cos)(
*
з
гри,
*
з
U
ekeU
Из второго уравнения получаем
0
0
=
ω
и
π
=
ω
1
. После подста-
новки этих значений в первое уравнение получим:
при 0
0
=
ω
=ω
105,2
)1(
1
гр0и,
−=
−
−
=
βγβ−
β−
ee
e
k
; (10.16)
при
π=
ω
=ω
1
122,21
)1(
1
гр1и,
=
−
+
=
βγβ−
β−
ee
e
k
. (10.17)
Решение (10.16) соответствует 0
гри,
<
k и не удовлетворяет рас-
сматриваемой САУ, поэтому принимаем решение (10.17), т.е.
122,21
гр1и,гри,
=
= kk .
)(Im
*
з
ωjA 25
и
=
k
20
и
=
k
π
=ω 0
=
ω
)(Re
*
з
ωjA
Рис. 10.6. Кривая
)(
*
з
ωjA для примера 10.2
0.5 0 0.5 1 1.5 2
0.5
1
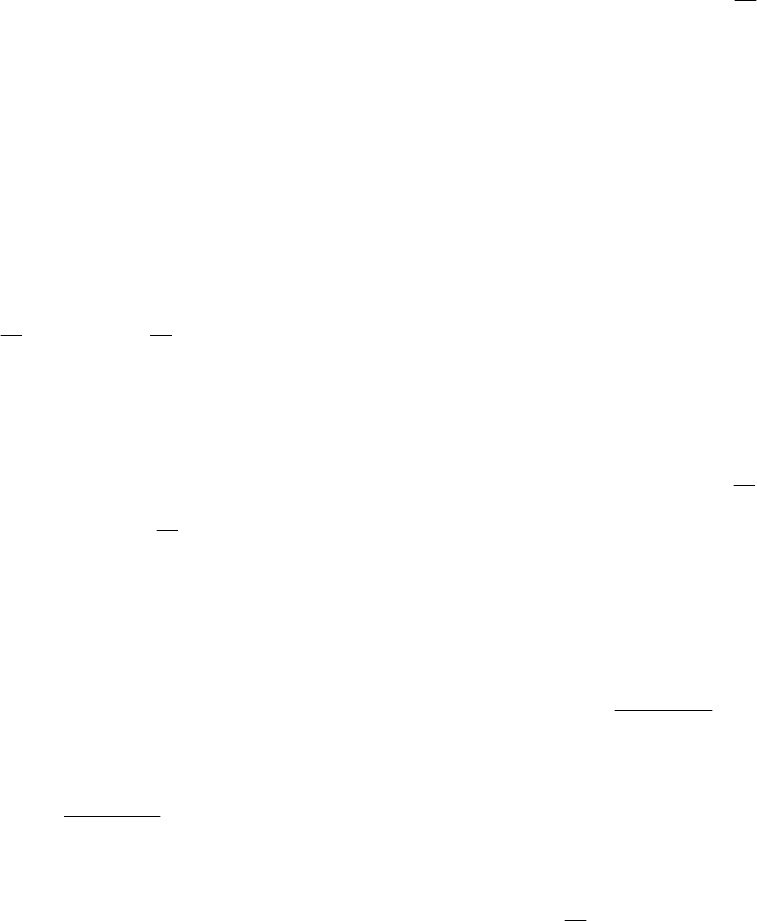
Формула (10.17) соответствует решению (10.11), полученному в
примере 10.1, поэтому границы устойчивости
|
2,0
гри,
)(
=β
γ= fk и
|
5,0
гри,
)(
=γ
β= fk будут отражаться кривыми, показанными на рис.
10.4.
При
гри,и
20 kk <= система будет устойчива и кривая )(
*
з
ωjA
будет проходить последовательно два квадранта комплексной плос-
кости (см. рис.10.6).
10.2.3. Аналог критерия Найквиста
При исследовании устойчивости систем с АИМ с помощью ана-
лога критерия Найквиста используется амплитудно-фазовая частот-
ная характеристика (АФЧХ) разомкнутой системы
)()0,(
*
p
*
p
ω=ω jWjW . Критерий устойчивости формулируется сле-
дующим образом.
Для того чтобы замкнутая система с АИМ, непрерывная
часть которой устойчива, была устойчивой необходимо и дос-
таточно, чтобы годограф АФЧХ разомкнутой системы
)(
*
p
ωjW
при возрастании ω от 0 до
π
не охватывал точку с координата-
ми
()
0,1 j− .
Как уже было отмечено в разделе 9.1, передаточная функция ра-
зомкнутой импульсной системы представляет собой дробно-
рациональную функцию по
q
e или z вида
)(
),(
),(
*
p
*
p
*
p
qA
qB
qW
ε
=ε
или
)(
),(
),(
*
p
*
p
*
p
zA
zB
zW
ε
=ε
. Если )(
*
p
qA имеет только простые полюсы, то
годограф АФЧХ имеет вид, изображенный на рис. 10.7, а. При нали-
чии в
)(
*
p
qA полюса, лежащего на мнимой оси, при 0=
ω
АФЧХ об-
ращается в бесконечность и ее годограф принимает вид, показанный
на рис. 10.7, б. Формулировка критерия не изменяется, только при
построении АФЧХ ее следует дополнить дугой бесконечно большо-
го радиуса, начинающейся от вещественной оси.
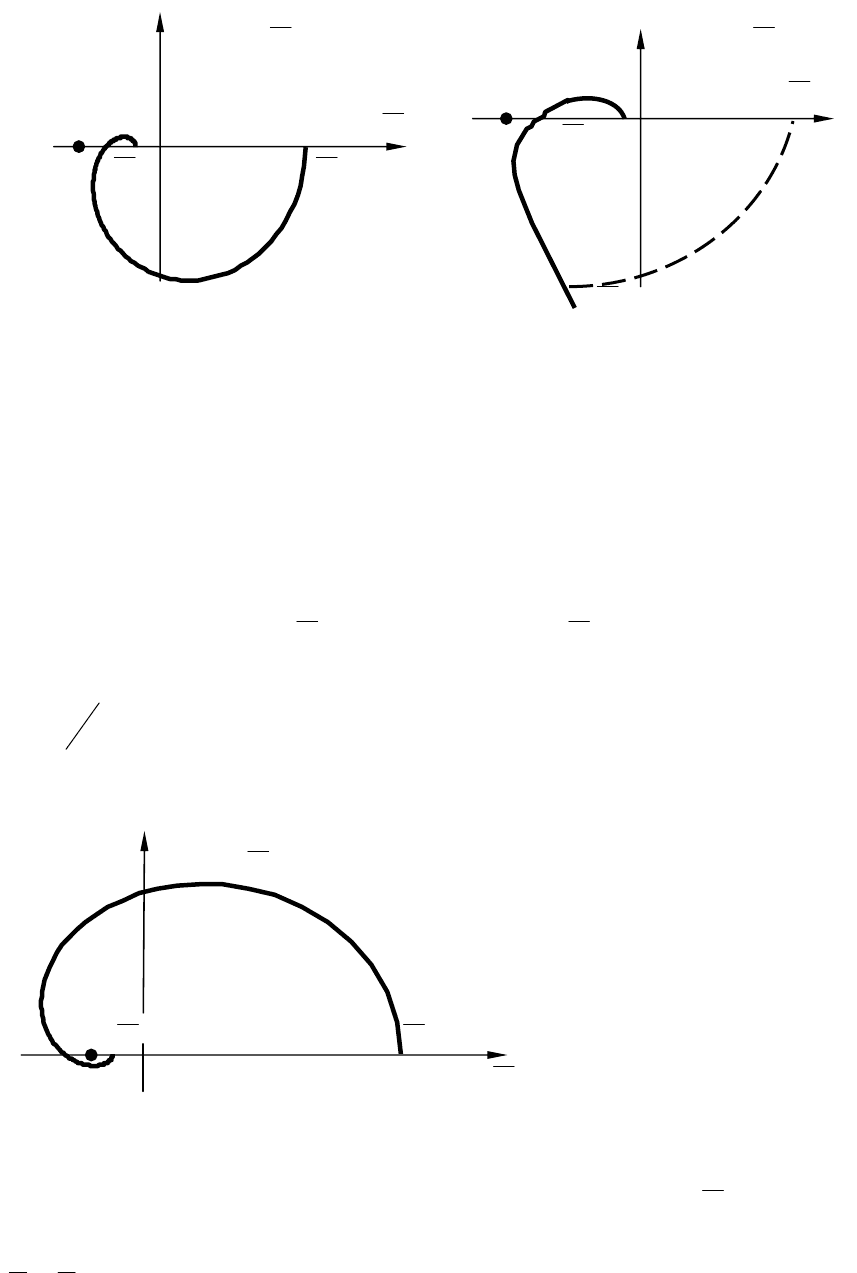
При неустойчивой непрерывной части формулировка критерия
Найквиста будет следующей:
Для того чтобы замкнутая система с АИМ, непрерывная
часть которой неустойчива, была устойчивой, необходимо и
достаточно, чтобы годограф амплитудно-фазовой частотной
характеристики
)(
*
p
ωjW при возрастании
ω
от 0 до π охваты-
вал точку с координатами
(
)
0,1 j
−
в положительном направле-
нии
2
s
раз, где
s
– число полюсов с положительной веществен-
ной частью передаточной функции разомкнутой импульсной
системы..
На рис. 10.8 при-
веден годограф
АФЧХ такой систе-
мы при
2=
s
. Не-
смотря на то, что не-
прерывная часть
системы
неустойчива,
замкнутая система с
АИМ будет устойчи-
вой, поскольку кри-
вая
)(
*
p
ωjW охваты-
вает точку
()
0,1 j−
1
2
2
2
==
s
раз.
)(Im
*
p
ωjW
)(Re
*
p
ωjW
-1
π
=
ω
0
0
=
ω
б
)(Im
*
p
ωjW
0
)(Re
*
p
ωjW
-1
π
=ω 0
=
ω
а
Рис. 10.7. Варианты годографа АФЧХ для устойчивой системы
)(Im
*
p
ωjW
1−
π
=ω
0
=
ω
0
)(Re
*
p
ωjW
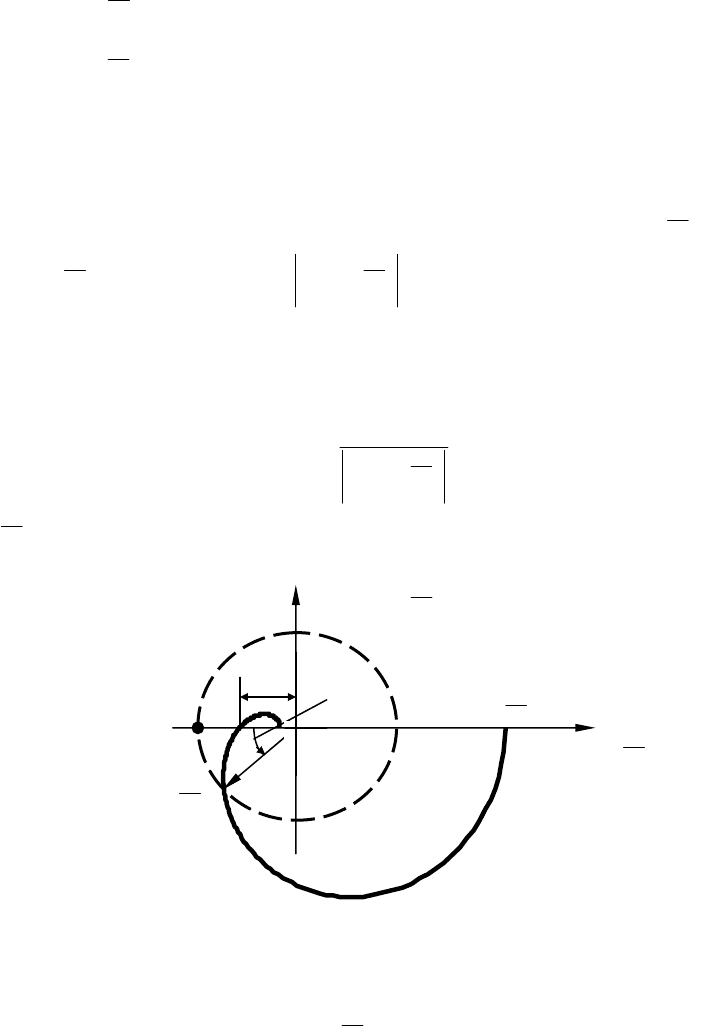
Рис. 10.8. Годограф АФЧХ устойчивой САУ
с неустойчивой непрерывной
ч
ас
ть
ю
Параметры, при которых годограф АФЧХ проходит через точку
()
0,1 j− , определяют границу устойчивости системы с АИМ. На гра-
нице устойчивости
=ω
−=ω
.0)(Im
,1)(Re
*
p
*
p
jW
jW
(10.18)
Удаление годографа от точки
(
)
0,1 j
−
характеризует запасы ус-
тойчивости по фазе и амплитуде (модулю, усилению). Запас устой-
чивости по фазе определяется как величина угла
π−ωϕ=δ )(
*
для
частоты
cp
ω
, при которой 1)(
*
p
=ωjW . Эта частота определяется в
точке пересечения годографа с окружностью единичного радиуса,
проведенной из начала координат (рис.10.9). Запас устойчивости
по амплитуде (модулю, усилению) определяется как величина,
обратная модулю АФЧХ
)(
1
*
p
ω
=
jW
a
, для частоты, при которой
π=ωϕ )(
*
.
Частоты, при которых
π=ωϕ )(
*
, называют критическими, а
частоту, при которой определяется запас устойчивости по амплитуде,
называют граничной. Если критическая частота одна, то она является
граничной.
)(Im
*
p
ωjW
1−
0
=
ω
)(Re
*
p
ωjW
cp
ω
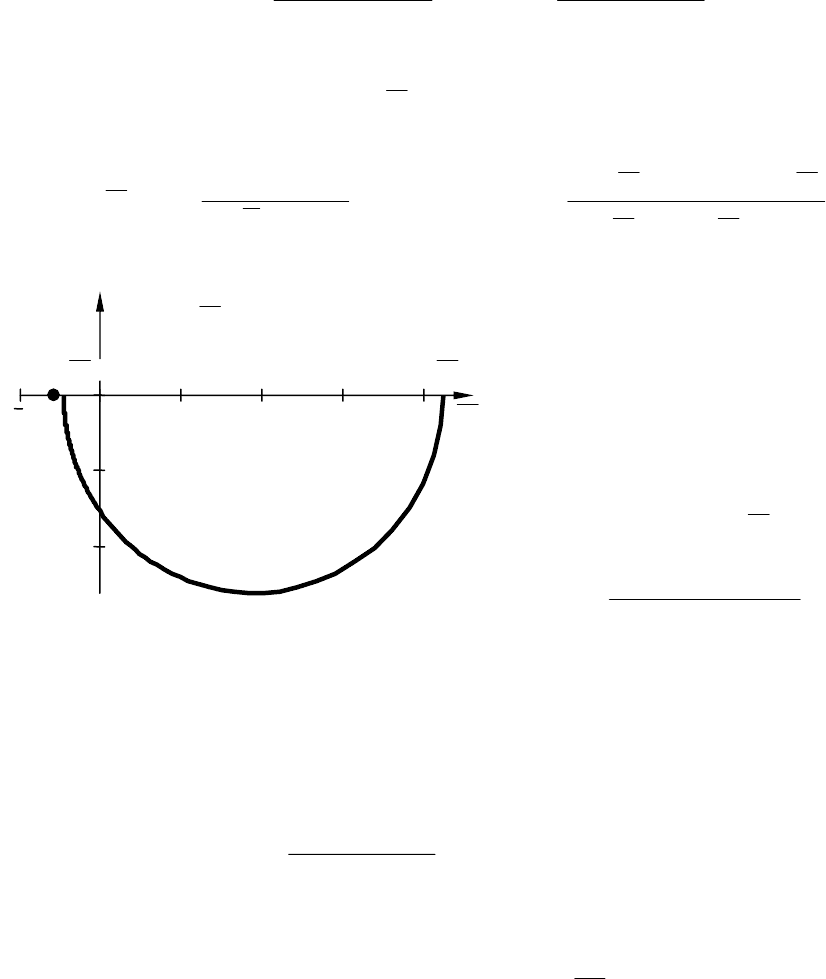
Рис. 10.9. К определению запасов
устойчивости
ψ
0
a
Пример 10.3. С помощью аналога критерия Найквиста опреде-
лить устойчивость и найти граничный коэффициент передачи для
САУ, приведенной на рис. 9.8, при следующих ее параметрах:
20
и
=k , 2,0=β , 5,0=γ .
Передаточная функция разомкнутой системы (см. пример 9.1)
при
0=ε имеет вид
β−
β−βχ
β−
β−
χ−β−
−
−
=
−
−
−=
ee
ee
ke
ee
ee
kqW
qq
q
)1(
1)0,(
и
)1(
и
*
p
.
Произведем замену
q на
ω
j
, тогда
β−
β−
βχβ−
β−ω
β
−
βχ
−ω
+
ω
ω−−ω
⋅−=
−
−
=ω
22
ии
*
p
sincos
sincos
)1(
)1(
)(
e
je
eek
ee
ee
kjW
j
.
На рис. 10.10 пока-
зан годограф АФЧХ
для рассматриваемой
САУ. Для заданных па-
раметров система ус-
тойчива, т.к. при гра-
ничной частоте
π
=ω
.1947,0
1
)1(
)(Re
и
*
p
−>−=
=
+
−−
=
=ω
β−
βχβ−
e
eek
jW
Если, в соответствии с (10.18), приравнять вещественную часть
АФЧХ к
1− , то выражение для граничного коэффициента передачи
будет иметь вид
(10.19)
На рис. 10.11 приведены зависимости граничного значения ко-
эффициента передачи
гри,
k от величины
0
T
T
=β
для различных зна-
чений относительной длительности импульса
γ
, рассчитанные по
формуле (10.19). Легко видеть, что с ростом
γ
значение
гри,
k
при
)(Im
*
p
ωjW
1− π=ω )(Re
*
p
ωjW
0
=
ω
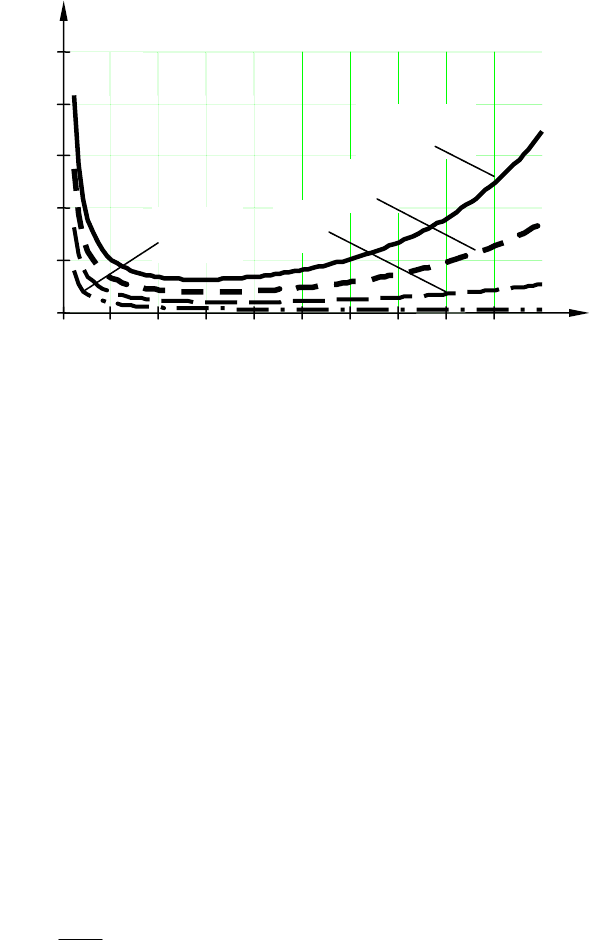
Рис. 10.10. Годограф АФЧХ для примера
10.3
2 0 2 4 6 8
4
2
1
=
)1(
1
)
, (
гри,
−
+
⋅
γ
β
β
χ
β−
β−
ee
e
k
фиксированной величине
β
уменьшается. Характеристики
),(
гри,
γ
β
k
при
1≠
γ
имеют четко выраженный минимум, а при
1=
γ
функция
),(
гри,
γ
βk , монотонно уменьшаясь, стремится к нулю.
11. ПЕРЕХОДНЫЕ И УСТАНОВИВШИЕСЯ
ПРОЦЕССЫ В ЗАМКНУТЫХ СИСТЕМАХ С
АИМ. ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ
11.1. Переходные характеристики замкнутых систем с
АИМ
Как было показано в предыдущих разделах, решетчатая функция
] ,[ εn
y
, определяющая закон изменения выходной величины в САУ с
АИМ, в общем случае может быть найдена по формуле обращения
[]
∑
∫
=
−
∞+
∞−
ε=ε
π
=ε
m
i
nq
e
jc
jc
qn
eqYdqeqY
j
ny
i
q
1
)1(*
з
*
з
),(Res),(
2
1
] ,[
~
, (11.1)
где
[
]
)1(*
з
),(Res
ˆ
−
ε
nq
e
eqY
i
q
означает вычет в точке
i
q
~
, а
)0,(),(),(
**
з
*
з
qFqWqY ⋅ε=ε .
гри,
k
β
Рис. 10.11. Границы устойчивости САУ
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
25
50
75
100
125
2,0
=
γ
3,0
5,0
1
=
γ

При произвольном воздействии ][n
f
выходная величина ],[
ε
n
y
представляет собой сумму вынужденной и переходной составляю-
щих, т.е.
] ,[] ,[] ,[
пв
ε
+
ε
=
ε
nynyny .
Переходная составляющая
] ,[
п
ε
ny определяет отклонение пере-
ходного процесса от установившегося значения. При
∞→
t
в устой-
чивой САУ
0] ,[
п
→εny
и в системе наступает вынужденный или
установившийся процесс
] ,[] ,[
вуст
ε
=
ε
nyny .
Если ][1][ nn
f
= , т.е.
1
)0,(
*
−
=
q
q
e
e
qF , то
),0()1(
1
),(lim
1
),(Res
*
з
*
з
0
)1(*
з
0
ε=
−
−
ε=
−
ε
→
−
=
We
e
e
qWe
e
e
qW
q
q
qn
q
nq
q
q
q
.
Если передаточная функция
),(
*
з
εqW имеет простые, отличные
от нуля, полюсы
i
q
~
, то вычет в каждом из таких полюсов определит-
ся из соотношения
,
)1)(
~
(
),
~
(
)(
1)0,(
),(
lim
1
),(Res
~
~
*
з
*
з
~
*
з
*
з
~
)1(*
з
~
nq
q
i
i
q
q
q
qn
qq
nq
q
q
qq
i
i
i
i
i
e
eqA
qB
ee
e
e
qA
qB
e
e
e
qW
−
ε
−=
=
−⋅
−
⋅
ε
=
−
⋅ε
→
−
=
&
где )
~
(
*
з i
qA
&
– производная от характеристического полинома по
q
e ,
вычисленная в полюсе
i
q
~
. Подставляя выражения для вычетов в
формулу (11.1), получим
∑
=
ε+ε=
−
ε
−ε=ε
m
i
nq
q
i
i
nynye
eqA
qB
Wny
i
i
1
пв
~
~
*
з
*
з
*
з
] ,[] ,[
)1)(
~
(
),
~
(
),0(] ,[
&
, (11.2)

Таким образом, при единичном воздействии установившееся зна-
чение равно значению передаточной функции замкнутой САУ с
АИМ при
0=q , т.е.
),0(] ,[
*
зуст
ε=ε Wny . (11.3)
Формула разложения (11.3) позволяет построить переходный
процесс для воздействия вида единичного скачка при
... ,3 ,2 ,1=n
и
10 ≤ε≤
, т.е. для любого момента времени, если передаточная
функция САУ с АИМ
),(
*
з
εqW задана в явном виде и известны ее
полюсы
i
q
~
.
Пример 11.1. Рассчитать переходные характеристики для систе-
мы с АИМ, приведенной на рис. 9.8 при
2,0
=
β
,
5,0
=
γ
,
1=
γ
и раз-
личных значениях коэффициента передачи
и
k
.
Воспользуемся результатами, полученными в примере 9.4. Пере-
даточные функции САУ:
≤ε<γ
−−−
−
γ≤ε≤
−−−
−−−
=ε
βγβ−
βε−βχ
βγβ−
βε−βχβ−βε−
.1
)]1(1[
)1(
,0
)]1(1[
)1()1(
),(
при
при
и
и
и
и
*
з
ekee
eee
k
ekee
eeeee
k
qW
q
q
q
q
(11.4)
Характеристический полином САУ при
1
≠
γ
:
)]1(1[)0,(
и
*
з
−−−=
βγ
β
−
ekeeqA
q
.
Полюс передаточных функций, определенный из уравнения
0)]1(1[)0,(
и
*
з
=−−−=
βγ
β−
ekeeqA
q
:
β−−−=
βγ
)]1(1ln[
~
и1
ekq .
Производная от характеристического полинома по
q
e :
{
}
1)]1(1[
)(
)(
и
*
з
=−−−=
βγβ−
ekee
ed
d
qA
q
q
&
.
