Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.


непрерывной частью (см. рис. 9.1, б). Приведенная непрерывная
часть в импульсной САУ всегда подвержена воздействию мгновен-
ных импульсов, следующих друг за другом в моменты времени
T
.
Реакция приведенной непрерывной части на мгновенный им-
пульс представляет собой импульсную переходную функцию
)(
t
w
.
Если мгновенный импульс произведен в момент времени
m
t
= , где
m – целое число, то реакция приведенной непрерывной части будет
равна
)( m
t
w − при m
t
≥ и 0 при m
t
<
, поэтому выражение реакции
)(
t
y приведенной непрерывной части на последовательность мгно-
венных импульсов можно записать следующим образом. В интервале
времени
10 ≤≤
t
)()0()(
t
w
x
t
y
=
,
в интервале времени
21
≤
≤
t
)1()1()()0()(
−
+
=
t
w
x
t
w
x
t
y ,
в интервале времени
32
≤
≤
t
)2()2()1()1()()0()(
−
+
−
+
=
t
w
x
t
w
x
t
w
x
t
y
,
и т.д. Вообще в интервале времени
1
+
≤
≤
n
t
n
∑
=
−=
n
m
mtwmxty
0
)()()( . (9.4)
Пусть в (9.4)
ε
+= n
t
, где n – целое число,
T
t∆
=ε
– относи-
тельное время, изменяющееся в интервале от 0 до 1,
T
– период по-
вторения,
t
∆ – время, отсчитываемое от начала каждого импульса.
Вводя решетчатые функции и обозначая
],[)( ],,[)( ],[)( ε
=
ε
+
ε
=
ε
+
= nwnwnynym
x
m
x
,
запишем (9.4) в виде
∑
=
−⋅=
n
m
mnwmxny
0
],[][),[
εε
,
(
)
10
<
ε
<
. (9.5)
Формула (9.5) устанавливает связь между входной и выходной
величинами импульсной системы, которые представлены решетча-
тыми функциями .В отличие от входной величины
][m
x
выходная
величина
],[ εny выражается смещенной решетчатой функцией, по-
зволяющей оценить поведение соответствующей ей непрерывной
функции
)(
t
y в любой произвольный момент времени.
Подвергнем обе части выражения (9.5)
D - преобразованию, тогда
получим
{}
ε−⋅=ε
∑
=
n
m
mnwmxny
0
],[][],[ DD .
По теореме линейности
{}{ }
],[][],[][
0
ε⋅=
ε−⋅
∑
=
nwnxmnwmx
n
m
DDD .
Вводя обозначения входной и выходной величин
{}
{
}
),(*],[ ),(*][
ε
=
ε
= qYnyqXnx DD
,
получим уравнение разомкнутой импульсной системы относительно
изображений
)(*),(),(*
*
p
qXqWqY ⋅ε=ε , (9.6)
где
{}
],[),(
*
p
ε=ε nwqW D . (9.7)
Уравнение (9.6) описывает процессы в системах с АИМ. При ма-
лых глубинах модуляции оно остается справедливым и для разомк-
нутых систем с ШИМ. Для систем с ВИМ, даже при малых глубинах
модуляции, это уравнение несправедливо.
Уравнение (9.6) позволяет ввести понятие
передаточной функ-
ции разомкнутой системы с АИМ
. Она представляет, с одной сто-

роны, отношение изображений (в смысле дискретного преобразова-
ния Лапласа) выходной величины разомкнутой САУ к входной, т.е.
)(*
),(*
),(
*
p
qX
qY
qW
ε
=ε
, (9.8)
а с другой, согласно (9.7) – дискретное преобразование Лапласа от
импульсной переходной функции приведенной непрерывной части.
В то же время
{
}
),(],[
пнч
ε=ε qWnw
1-
D , где ),(
пнч
εqW – переда-
точная функция приведенной непрерывной части в смысле дискрет-
ного преобразования Лапласа. Если
)(
пнч
qW – передаточная функ-
ция приведенной непрерывной части в смысле обычного преобразо-
вания Лапласа, то, зная ее, можно определить соответствующее ей
изображение
),(
пнч
εqW (в литературе [2, 11 ] эту операцию назы-
вают
D -преобразованием). Следовательно, передаточная функция
разомкнутой САУ с АИМ определяется соотношением
{
}
),(),(),(
пнчпнч
*
p
ε=ε=ε qWqWqW D , (9.9)
т.е.
передаточная функция разомкнутой системы с АИМ равна
передаточной функции ее приведенной непрерывной части в
смысле дискретного преобразования Лапласа
.
Благодаря замене
z
e
q
=
, формулы (9.8), (9.9) можно получить и
для
z -преобразования:
)(*
),(*
),(
*
p
zX
zY
zW
ε
=ε
, (9.10)
{
}
)(),(),(
пнчпнч
*
p
qWzWzW
z
L=ε=ε . (9.11)
Символьное обозначение
{
}
z
L , аналогично
{}
D , называется
модифицированным
z - преобразованием и означает связь между
изображениями в обычном преобразовании Лапласа и в
Z
-
преобразовании.
Для преобразований
{
}
D и
{
}
z
L имеет место важное свойство
– умножение изображения на
q
e
γ
−
, в соответствии с которым [11 –
13]
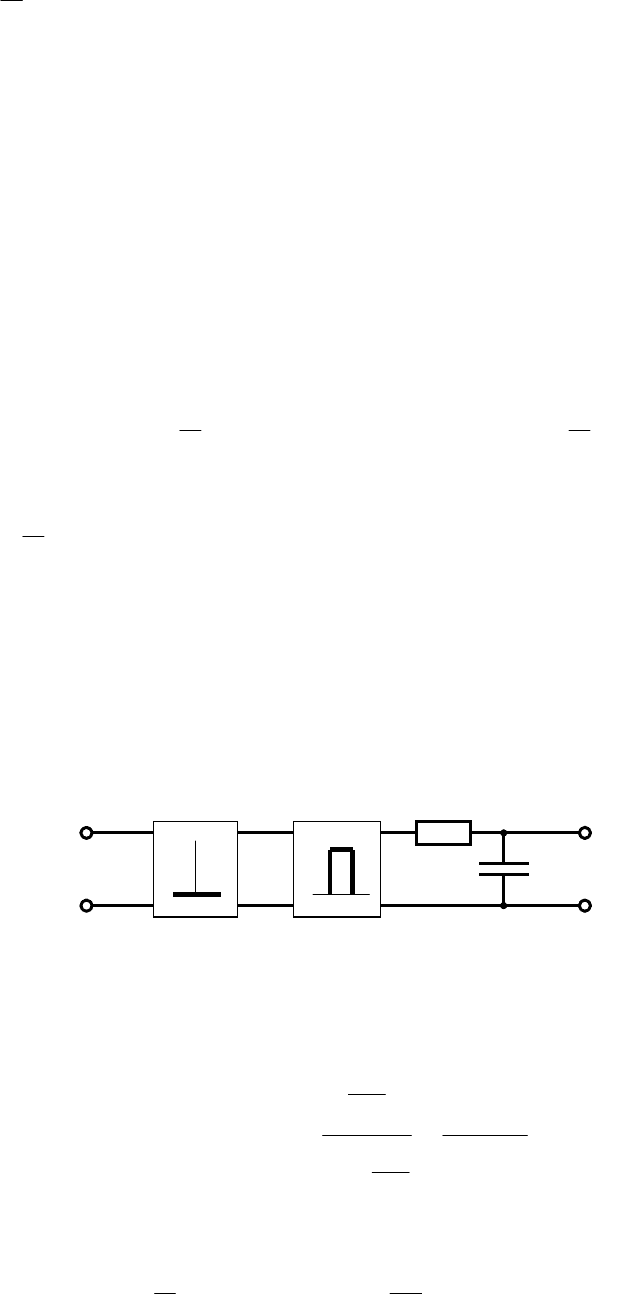
{}
≤ε≤γγ−ε
γ≤ε≤γ−ε+
=
−
γ−
.1 ),(*
,0 )1,(*
)(
при
при
qF
qFe
qFe
q
q
D
(9.12)
{}
≤ε≤γγ−ε
γ≤ε≤γ−ε+
=
−
γ−
.1 ),(*
,0 )1,(*
)(
при
при
1
zF
zFz
qFe
q
z
L
(9.13)
Рассмотрим несколько примеров вывода передаточных функций
разомкнутых систем с АИМ.
Следует отметить одно важное обстоятельство. Для перехода к
относительному масштабу времени в изображениях всех воздейст-
вий, а также в передаточной функции формирующего элемента нуж-
но заменить
p
на
T
q
и умножить изображение на
T
1
. При этом в пе-
редаточных функциях непрерывной части производится лишь замена
p
на
T
q
.
Пример 9.1.
На рис. 9.3 изображена элементарная система с АИМ, непрерыв-
ная часть которой представляет собой RC-цепь. Требуется получить
передаточную функцию этой системы с помощью дискретного пре-
образования Лапласа.
Передаточная функция непрерывной части
,
1
1
1
1
)(
0
нч
+
=
+
=
pT
Cp
R
Cp
pW
где
RCT =
0
–постоянная времени RC-цепи.
Полагая
T
q
p =
и обозначив
0
T
T
=β
, получим
ИИЭ ФЭ R
)(
t
x
C
)(
t
y
Рис. 9.3. Элементарная САУ с АИМ

β+
β
=
+
β
=
+
==
=
q
q
T
q
T
T
q
WqW
1
1
1
1
)(
0
нчнч
.
Передаточная функция формирующего элемента, производящего
прямоугольные импульсы относительной длительности
γ
и ампли-
тудой
и
k , в соответствии с (9.2) равна
q
ek
qW
q
)1(
)(
и
ф
γ
−
−
=
. Тогда
для приведенной непрерывной части получим
()
β+
β
−
β+
β
=
=
β+
−β
=⋅=
γ−
γ
−
)()(
)(
)1(
)()(
и
и
нчфпнч
qq
e
qq
k
qq
ek
qWqWqW
q
q
. (9.14)
Разложим изображение
)1( +β
β
qq
на элементарные дроби и по
табл. 8.1 найдем изображения в смысле дискретного преобразования
Лапласа, т.е. проведем
{
}
D - преобразование для получившихся со-
ставляющих:
β+
−=
+β qqqq
11
)1(
1
,
{}
1
1
1
−
==
q
q
e
e
q
DD
,
{
}
βε−
β−
εβ−
−
==
β+
e
ee
e
e
q
q
q
n ).(
1
DD
.
Таким образом, для первого слагаемого в (9.14) по теореме ли-
нейности будем иметь
),(*
1
)(
1
ε=
−
−
−
=
β+
β
βε−
β−
qFe
ee
e
e
e
qq
q
q
q
q
D
.
Используя соотношение (9.12), получим изображение для второ-
го слагаемого в (9.14):
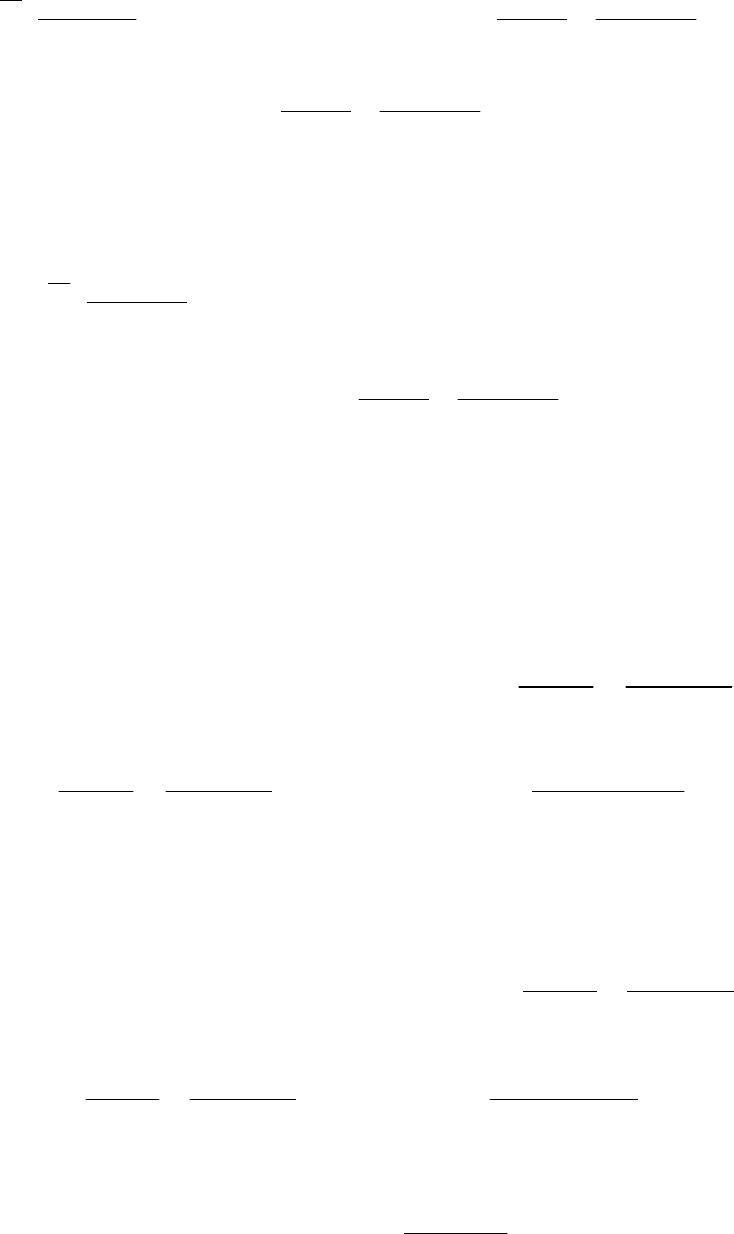
- при
γ
≤
ε
≤0
).,(
1
1
1
1
)1,(*
)(
*
21
)1(
)1(
1
ε=
−
−
−
=
=
−
−
−
=γ−+ε=
β+
β
γ−ε+β−
β−
γ−ε+β−
β−
−−
γ−
qFe
eee
e
ee
e
e
e
eqFe
qq
e
qq
q
q
q
q
qq
q
D
- при
1≤≤
ε
γ
),,(
1
),(*
)(
*
22
)
1
ε=
−
−
−
=
=γ−ε=
β+
β
γ−βε−
β−
−
γ−
qFe
ee
e
e
e
qFe
qq
e
q
q
q
q
q
q
D
Таким образом, передаточная функция рассматриваемой САУ с
АИМ будет состоять из двух составляющих и выразится соотноше-
ниями:
- при
γ
≤
ε
≤0
[]
,1
1
1
1
1
),(),(),(
)1(
и
)1(
и
*
21
*
1и
*
p
−
−
−=
−
−
−
−
−
−
−
−
=ε+ε=ε
βε−
β−
γ−β−
γ−ε+β−
β−
βε−
β−
e
ee
ee
ke
eee
e
ee
e
e
e
kqFqFkqW
q
q
qq
q
q
q
q
- при
1≤
ε
≤
γ
[]
.
)1(
1
1
),(),(),(
)(
и
)(
и
*
22
*
1и
*
p
γ−εβ−
β−
βγ−
γ−εβ−
β−
βε−
β−
−
−
=
−
−
−
−
−
−
−
−
=ε+ε=ε
e
ee
ee
ke
ee
e
e
e
e
ee
e
e
e
kqFqFkqW
q
q
q
q
q
q
q
q
q
q
При
1=
γ
−
−
−=ε
βε−
β−
e
ee
e
kqW
q
q
1
1),(
и
*
p
.

При переходе к
Z
-преобразованию в результате замены
z
e
q
=
передаточные функции САУ примут вид:
- при
γ
≤ε
≤
0
−
−
−=ε
βε−
β−
γ−β−
e
ez
ez
kzW
)1(
и
*
p
1),(
;
- при
1≤
ε
≤
γ
)(
и
*
p
)1(
),(
γ−εβ−
β−
βγ
−
−
−
=ε e
e
z
ze
kzW
;
- при
1=
γ
1
1),(
и
*
p
−
−
−=ε
βε−
β−
e
ez
z
kzW
.
Пример 9.2.
Пусть в САУ, изображенной на рис. 9.3, передаточная функция
непрерывной части
p
k
pW =)(
нч
, а коэффициент передачи форми-
рующего элемента
1
и
=k . Получить передаточную функцию САУ с
помощью
Z
-преобразования.
Передаточная функция приведенной непрерывной части
2
пнчфэнч
)1(
)( ,
1
)( ,)(
|
q
ekT
qW
q
e
qW
q
kT
p
k
qW
qq
T
q
p
γ
−
γ
−
=
−
=
−
===
.
Согласно табл. 8.1,
ε
−
+
−
=
1
)1(
22
z
z
z
z
k
q
kT
z
L , тогда по
формуле (9.13) получим:
при
γ
≤
ε≤0
−
γ−ε+
+
−
=
γ−ε+
−
+
−
=
−γ−
1
1
)1(
1
)1(
1
)1(
2
1
22
z
z
kz
z
z
z
z
ke
q
kT
q
z
L
,
при
1
≤
ε<γ
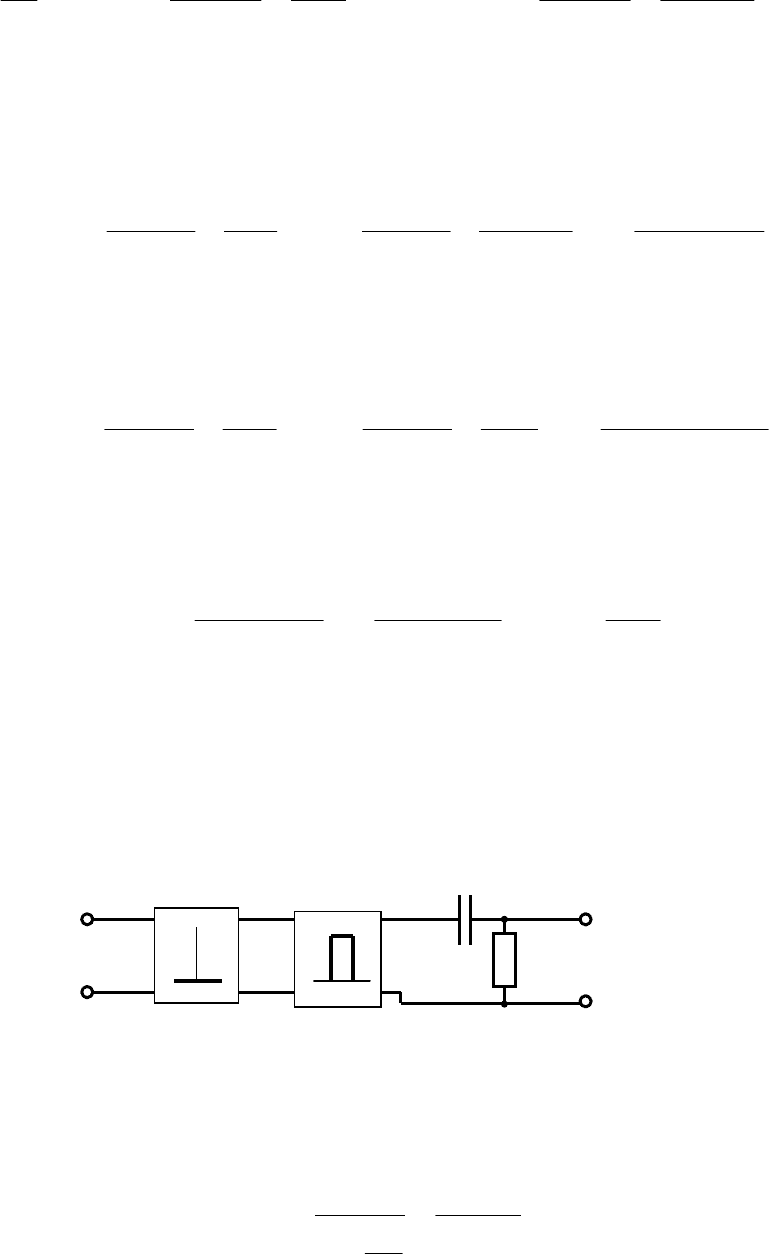
−
γ−ε
+
−
=
γ−ε
−
+
−
=
−γ−
1
)(
)1(
)(
1
)1(
2
1
22
z
z
z
z
kz
z
z
z
z
ke
q
kT
q
z
L .
Передаточная функция САУ будет иметь вид:
при
γ
≤
ε≤0
,
1
)(
1
1
)1(
1
1
)1(
),(
22
*
p
−
γ−ε−ε
=
−
γ−ε+
+
−
−
ε
−
+
−
=ε
z
z
k
z
z
k
z
z
z
z
kzW
при
1
≤
ε<γ
.
1
)1(
1
)1(
1
1
)1(
),(
22
*
p
−
γ−−ε−ε
=
−
γ−ε
+
−
−
ε
−
+
−
=ε
z
z
k
z
z
k
z
z
z
z
kqW
При
1=γ
−
+ε=
−
+
−
ε
=
−
−
ε
−ε
=ε
1
1
1
1)1(
1
)1(
),(
*
p
z
k
z
z
k
z
z
kqW
.
Пример 9.3.
На рис. 9.4 изображена система с АИМ, непрерывная часть кото-
рой представляет реальное дифференцирующее звено. Необходимо
получить передаточную функцию такой системы, используя
Z
-
преобразование.
Передаточная функция непрерывной части
,
1
1
)(
0
0
нч
+
=
+
=
pT
pT
Cp
R
R
pW
где
RCT =
0
– постоянная времени.
C
R
Рис. 9.4. Структурная схема САУ с АИМ
д
ля п
р
име
р
а 8.3
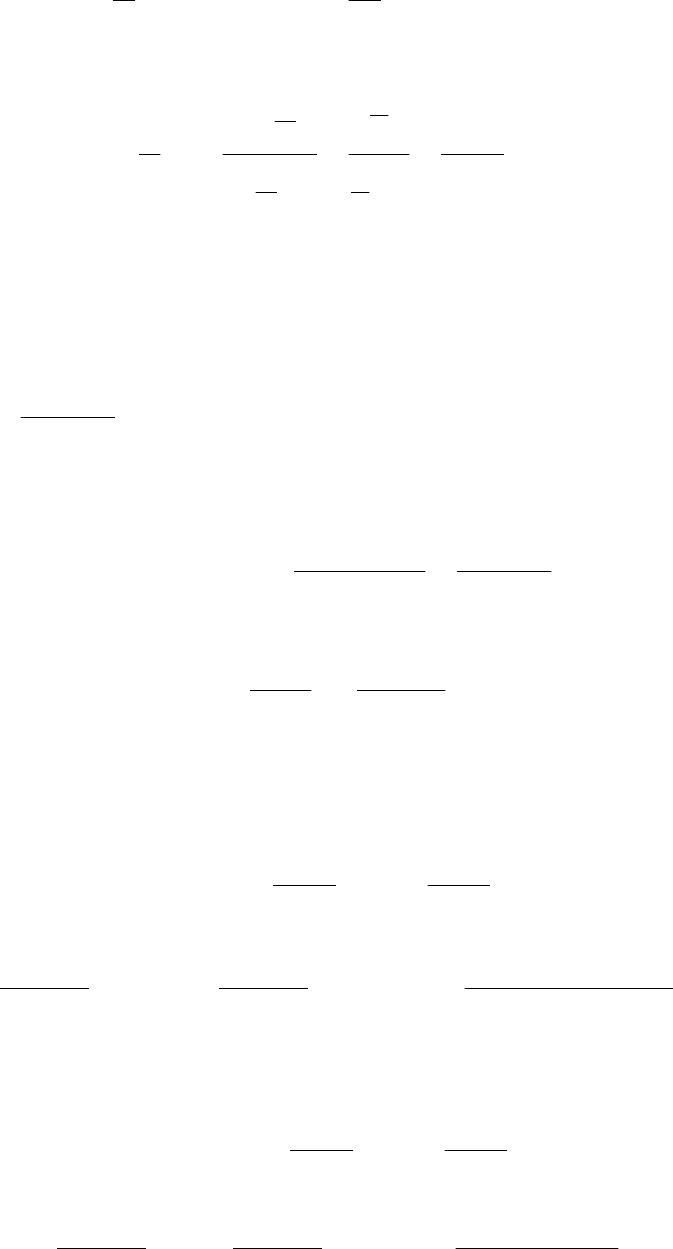
Полагая
T
q
p =
и обозначив
0
T
T
=β
, получим
β+
=
+
β
β
=
+
==
=
q
q
q
q
T
q
T
T
q
T
T
q
WqW
11
)(
0
0
нчнч
.
Пусть формирующий элемент производит прямоугольные им-
пульсы относительной длительности
γ
и единичной амплитуды, то-
гда, в соответствии с (9.2), его передаточная функция равна
q
e
qW
q
γ
−
−
=
1
)(
ф
. Передаточная функция непрерывной части будет
иметь вид
()
β+
−
=
β+
−
=⋅=
γ
−
γ
−
q
e
qq
eq
qWqWqW
qq
1
)(
)1(
)()(
нчфпнч
.
Согласно табл. 8.1,
βε−
β−
−
=
β+
e
ez
z
q
z
1
L
, тогда по формуле
(9.13) получим:
при
γ
≤
ε≤0
[]
;
1
),(
)1(
)1(1
*
p
β−
γ−β−βε−
γ−ε+β−
β−
−βε−
β−
χ−
−
−
=
−
−
−
=
=
β+
−
β+
=ε
ez
eze
e
ez
z
ze
ez
z
q
e
q
zW
q
zz
LL
при
1
≤
ε<
γ
=
β+
−
β+
=ε
χ−
q
e
q
zW
q
zz
LL
1
),(
*
p
(
)
.
1
)(
β−
βγ
β
ε
−
γ−εβ−
β−
βε−
β−
−
−
=
−
−
−
=
ez
eze
e
ez
z
e
ez
z

При
1=
γ
(
)
.
1
),(
*
p
β−
β
ε
−
−
−
=ε
ez
ze
qW
Приведенные примеры показывают, что передаточная функция
разомкнутой импульсной системы представляет собой дробно-
рациональную функцию по
q
e или z , т.е.
)(
),(
),(
*
p
*
p
*
p
qA
qB
qW
ε
=ε
,
)(
),(
),(
*
p
*
p
*
p
zA
zB
zW
ε
=ε
,
где
,)(
),()()()(),(
01
)1(
1
*
p
01
)1(
1
*
p
aeaeaeaqA
bebebebqB
qmq
m
qm
m
qkq
k
qk
k
++⋅⋅⋅++=
ε+ε+⋅⋅⋅+ε+ε=ε
−
−
−
−
или
,)(
),()()()(),(
01
1
1
*
p
01
1
1
*
p
azazazazA
bzbzbzbzB
m
m
m
m
k
k
k
k
++⋅⋅⋅++=
ε+ε+⋅⋅⋅+ε+ε=ε
−
−
−
−
причем
m
k
≤ . Это свойство передаточных функций САУ с АИМ по-
требуется при дальнейшем изучении материала, посвященного этим
системам.
9.2. Основные правила преобразования структурных
схем. Уравнения и передаточные функции замкнутых
систем с АИМ
Если САУ с АИМ содержит один импульсный элемент, а ее не-
прерывная часть представляет собой различные комбинации соеди-
нения типовых звеньев, то правила преобразования структурных
схем для таких систем аналогичны правилам преобразования струк-
турных схем для непрерывных САУ.
Рассмотрим применение этих правил для замкнутых систем с
АИМ. Пусть замкнутая САУ с АИМ имеет структуру, приведенную
на рис. 9.5, а. Здесь
)( ),(
21
qFqF
– изображения внешних воздейст-
вий,
)(
ф
qW – передаточная функция формирующего элемента,
)( ),(
21
qWqW – передаточные функции непрерывной части,
