Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

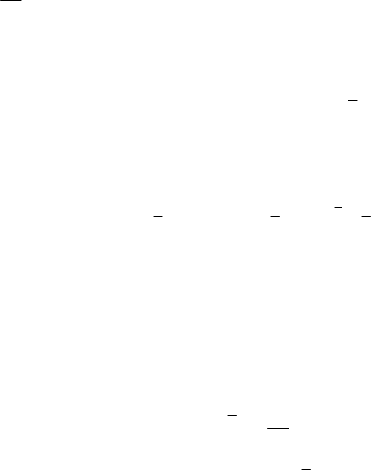
∑
∞
=
−
ε=ε
0
],[),(*
n
qn
enfqF .
(8.4)
Здесь
ω+
σ
=
j
q – комплексное число, называемое параметром
преобразования,
ε – вещественный параметр (смещение решетчатой
функции). Если сравнить (8.3) и (8.4) с определением обычного пре-
образования Лапласа непрерывной функции
)(
t
f
и при
pT
q =
{}
∫
∞
−
==
0
)()()( tdetftfqF
tq
L
,
то легко заметить аналогию между ними. Интеграл с бесконечным
верхним пределом соответствует бесконечной сумме, т.е. ряду в (8.3)
или (8.4); непрерывная переменная
T
t
t =
– дискретная переменная
n; произвольной непрерывной функции )(
t
f
– решетчатая функция
][n
f
или смещенная решетчатая функция ],[
ε
n
f
.
Соотношение (8.4) устанавливает соответствие между решетча-
той функцией
],[ εn
f
и функцией ),(*
ε
q
F
комплексной переменной
q . По аналогии с обычным преобразованием Лапласа первую функ-
цию называют оригиналом, а вторую – изображением. Символьно
соотношение между оригиналом и изображением записывают в виде
{
}
][)(* nfqF D=
, ][)(* n
f
q
F
⇔
,
или
{
}
],[),(*
ε
=ε nfqF D , ],[),(* ε
⇔
ε
n
f
q
F
.
Изображения, полученные по соотношениям (8.3) или (8.4), будут
содержать трансцендентный множитель – функцию вида
nq
e
−
. Эта
функция обладает таким свойством, что при
jr
q
π
=
2 и любом целом
r
функция 1
2
=
π
jr
e , следовательно,
qjrq
ee
=
π
+
2
и
)(*)2(* q
F
jr
q
F
=
π
+ . (8.5)
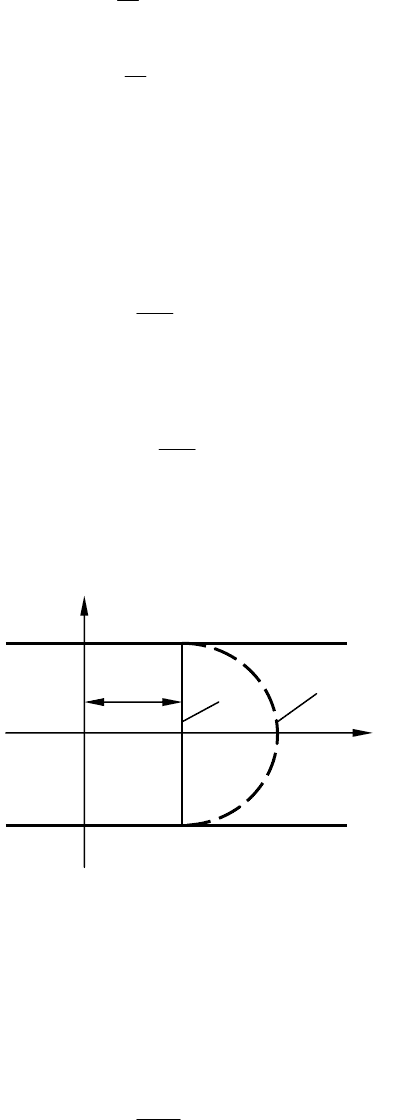
Это означает, что изображение
)(* q
F
представляет собой пе-
риодическую функцию вдоль мнимой оси комплексной плоскости
ω
σ
j
q += с периодом
π
2 .Поэтому изображение )(* q
F
, вследст-
вие его периодичности, можно рассматривать в полосе
π
<
<π− qIm
или
π<ω<π− .
Существует и обратное соотношение – по изображениям
)(* q
F
и
),(* εq
F
можно восстановить решетчатые функции ][n
f
и
],[ εn
f
:
∫
π+σ
π−σ
π
=
j
j
qn
j
dqeqFnf )(*][
2
1
, (8.6)
∫
π+σ
π−σ
π
ε=ε
j
j
qn
j
dqeqFnf ),(*],[
2
1
. (8.7)
Формулы (8.6) и (8.7) называют-
ся формулами обращения и позво-
ляют осуществить обратное дис-
кретное преобразование Лапласа.
Интегрирование вдоль прямой
L
можно заменить интегрированием
вдоль любой кривой
Γ (рис. 8.3),
лежащей справа от отрезка
L
. Ве-
личина
c – произвольная положи-
тельная постоянная, большая абс-
циссы сходимости функции
)(* q
F
.
Если особые точки
ν
q изображения
)(* q
F
расположены правее прямой
L
, то вычисление интеграла
(8.6) можно произвести через вычеты
[]
)1(
)(*Re2)(*
2
1
][
−
=
π+σ
π−σ
∑
∫
ν
π=
π
=
nq
qq
j
j
qn
eqFsjdqeqF
j
nf . (8.8)
Рис. 8.3 К восстановлению
решетчатых функций
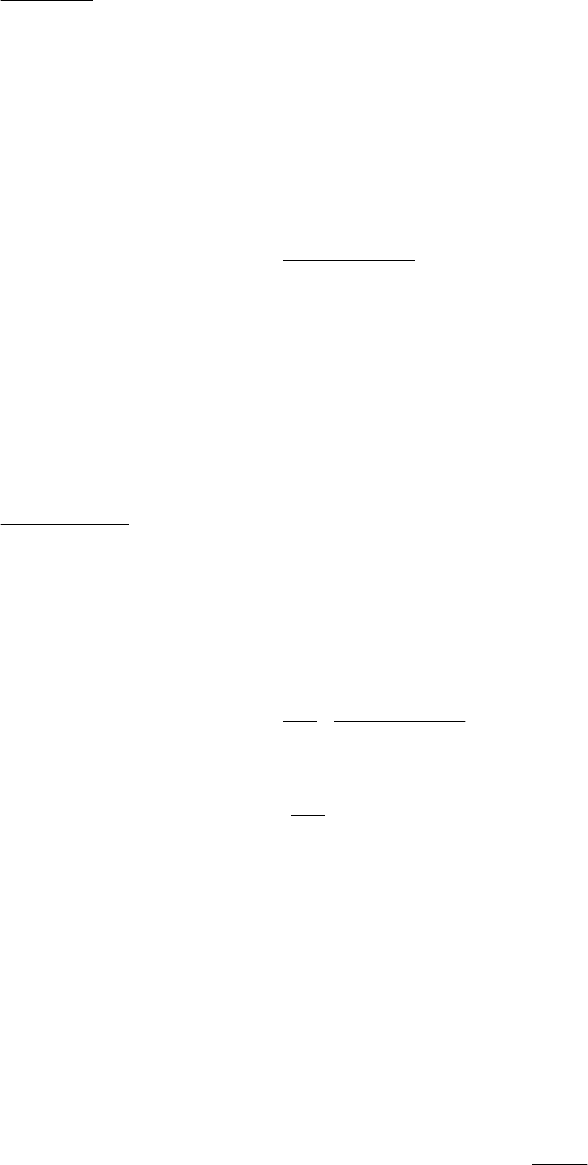
Пример 8.3.
Найти оригинал, соответствующий изображению
α
−
=
ee
e
qF
q
q
)(* .
Заданное изображение имеет один простой полюс в точке
α
=
q
(именно при этом значении
q знаменатель )(* q
F
обращается в
нуль). Тогда, согласно формуле (8.8) и теории вычетов [1 - 3], полу-
чим
[]
(
)
.lim
lim)(*Res][
)1(
)1(
nqn
q
q
q
nqq
q
nq
q
ee
ee
ee
ee
eqFnf
α
α→
α
α
−
α→
−
α=
==
=−⋅
−
⋅
==
Пример 8.4.
Найти оригинал, соответствующий изображению
2
)(
)(*
α
−
=
ee
e
qF
q
q
.
Заданное изображение в точке
α
=
q имеет один полюс кратно-
сти 2. Согласно формуле (8.8) и теории вычетов [1- 3,11], получим
[]
()
.limlim
)(
)(
lim)(*Res][
)1()1(
2
2
)1(
)1(
−⋅α−
α→α→
α
α
−
α→
−
α=
===
=
−⋅
−
⋅
==
nnq
q
qn
q
q
q
nqq
q
nq
q
nenee
dq
d
ee
ee
ee
dq
d
eqFnf
Приведенные примеры наглядно иллюстрируют общность между
обычным преобразованием Лапласа и дискретным преобразованием.
Свойства дискретного преобразования Лапласа аналогичны свойст-
вам преобразования Лапласа для непрерывных функций. Здесь также
имеют место теоремы линейности, запаздывания, свертки и т.д. Спе-
цифика заключается только в дискретности преобразуемых функций.
Так, например, в обычном преобразовании Лапласа по теореме о
дифференцировании изображений
{
}
)()1()( pF
dp
d
tft
m
m
mm
−=L . Для

дискретного преобразования Лапласа эта теорема выглядит так:
{}
)(*)1(][ qF
dq
d
nfn
m
m
mm
−=D .

Следует отметить еще одно важное обстоятельство. Поскольку
существует однозначная связь между непрерывной и решетчатой
функциями, то следует ожидать и аналогичную связь между их изо-
бражениями. Правда, поскольку
pT
q
=
и
T
q
p =
, при переходе в
изображениях непрерывных функций к переменной
q его нужно ум-
ножить на период квантования
T
. В литературе [11] имеются об-
ширные таблицы соответствия изображений
{}
)()( tfqF L= и
{
}
],[),(* ε=ε nfqF D
.
8.3. Z-преобразование
Несмотря на свою наглядность, дискретное преобразование Лап-
ласа не получило широкого применения при исследовании САУ с
АИМ. Это, в первую очередь, связано с тем, что изображения ре-
шетчатых функций содержат трансцендентный множитель
nq
e
−
и
соответствующие передаточные функции становятся иррациональ-
ными. Более широкое распространение получило так называемое Z-
преобразование [12 – 14], позволяющее получить передаточные
функции импульсных систем в дробно-рациональной форме.
Под Z-преобразованием понимают преобразование вила
∑
∞
=
−
=
0
][)(*
n
n
znfzF , (8.9)
или
∑
∞
=
−
ε=ε
0
],[),(*
n
n
znfzF . (8.10)
Здесь функции
)(*
z
F
и ),(*
ε
z
F
можно рассматривать как глав-
ную часть ряда Лорана, коэффициенты которого равны решетчатым
функциям
][n
f
и ],[ εn
f
.
Сравнивая формулы(8.9), (8.10) с выражениями (8.3), (8.4) можно
сделать вывод о том, что Z-преобразование получается из дискрет-
ного преобразования Лапласа путем замены множителя
q
e на
n
z .
Если произвести такую замену в формуле (8.7), то можно полу-
чить формулу обращения для Z-преобразования:
∫
Γ
+−
π
=
1
1
)(*
2
1
][ dzzzF
j
nf
n
, (8.11)
где
1
Γ
– окружность радиуса
c
e . Эта формула представляет собой
известное выражение коэффициентов ряда Лорана и позволяет осу-
ществить обратное Z-преобразование.
Символически прямое и обратное Z-преобразование обозначают-
ся так:
{}
][)(* nfzF Z= ,
{
}
)(*][ zFnf
1-
Z= ,
или
{}
],[),(*
ε
ε
nfzF Z
=
,
{
}
),(*],[
εε
zFnf
1-
Z= .
Все теоремы для Z-преобразования получаются из дискретного
преобразования Лапласа путем простой замены переменной
z
e
q
=
.
Приведем некоторые из них
8.3.1. Теорема линейности
∑∑
==
λ=
λ
m
i
ii
m
i
ii
zFnf
1
*
1
)(][Z ,
где
i
λ – коэффициенты, не зависящие от
z
и n ; )(
*
zF
i
– изображе-
ния решетчатых функций
][nf
i
.
8.3.2. Теорема запаздывания
{}
)(*][ zFenf
α
=α
m
mZ ,
где
α – величина запаздывания (опережения) решетчатой функции
][n
f
, )(*
z
F
– ее изображение.

8.3.3. Теорема смещения изображений
{
}
][)(* nfezF
n
λ
=λ±
m
Z ,
(
)
const
=
λ
.
8.3.4. Теорема об изображении разностей.
Для первой разности
][]1[][ n
f
n
f
n
f
−
+
=
∆
{}
]0[)(*)1(][ fzzFznf
⋅
−
−
=
∆Z .
Для второй разности
][]1[][
2
nfnfnf ∆−+∆=∆
{
}
]0[]0[)1()(*)1(][
22
fzfzzzFznf ∆⋅−⋅−−−=∆Z .
Для
k
-той разности ][]1[][
)1()1(
nfnfnf
kkk −
−
∆−+∆=∆
{}
∑
−
=
−−
∆⋅−−−=∆
1
0
)(1)(
]0[)1()(*)1(][
k
i
iikkk
fzzzFznfZ .
8.3.5. Теорема о начальном значении оригина-
ла
)(*lim][lim]0[
0
zFnff
zn ∞→→
=
=
.
8.3.6. Теорема о конечном значении оригинала
)(*)1(lim][lim][
0
zFznff
zn
−
=
=∞
→∞→
.
Соответствие между изображениями
)(q
F
непрерывных функ-
ций
)(
t
f
при pTq
T
t
t == , и изображениями ),(* ε
z
F
в области
Z-преобразования для смещенных решетчатых функций
],[ εn
f
уста-
навливается в табл. 8.1. Изображения
)(* z
F
для функций
][n
f
можно определить, полагая
0
=
ε
в изображении ),(* ε
z
F
. Здесь
также
T
ω=ω – относительная частота.
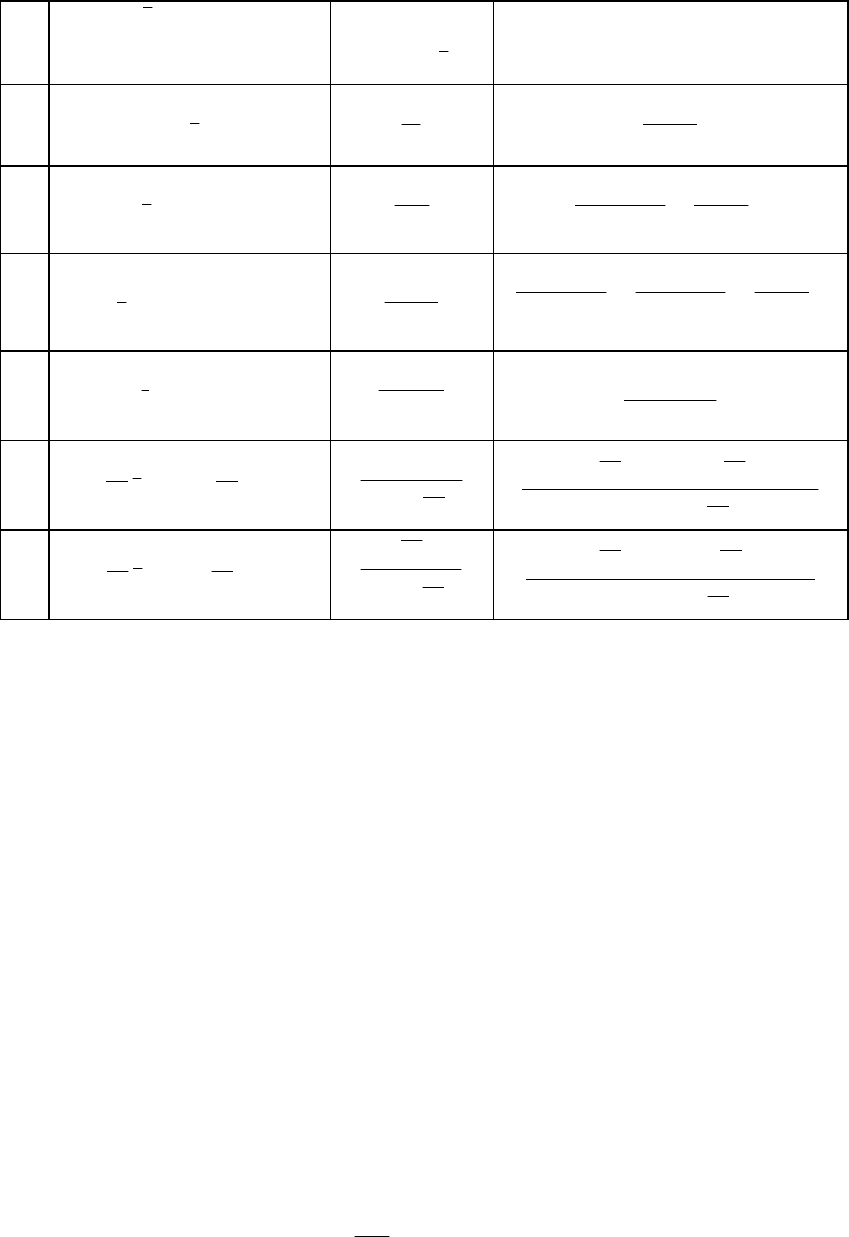
Таблица 8.1
№
],[)( ε
=
n
f
t
f
{}
)(
)(
tf
q
F
L=
=
{}
],[),(* ε=
ε
nfzF Z
1
)(1
t
q
1
1−
z
z
2
ε+= n
t
2
q
T
ε
−
+
−
1
)1(
2
z
z
z
z
3
22
)( ε+= nt
3
2
2
q
T
ε
−
+
−
+
−
+
1
)1(
2
)1(
)1(
23
z
z
z
z
z
zz
4
)( ε+α−α−
=
nt
ee
α+q
1
α−
αε−
−
⋅
ez
ez
5
)(coscos ε+ω=ω n
t
22
ω
+q
q
1cos2
)1(coscos
2
2
+ω
−
ε−ω−εω
zz
zz
6
)(sinsin ε+ω=ω n
t
22
ω
ω
+q
1cos2
)1(sinsin
2
2
+ω
−
ε−ω+εω
zz
zz
9. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ С
АИМ
9.1.
Передаточные функции разомкнутых систем с
АИМ
Разомкнутая импульсная система представляет собой последова-
тельное соединение импульсного элемента и непрерывной части, ко-
торую будем считать линейной (рис. 9.1, а). На вход импульсного
элемента подается непрерывное воздействие
)(
t
x
, а на его выходе
формируется импульсная последовательность, характер которой оп-
ределяется видом модуляции сигнала
)(
t
x
. Помимо вида модуляции,
импульсный элемент характеризуется периодом квантования
T
или
частотой квантования
T
π
=ω
2
0
, коэффициентом передачи и формой
модулируемых выходных импульсов
)(
м
tx .
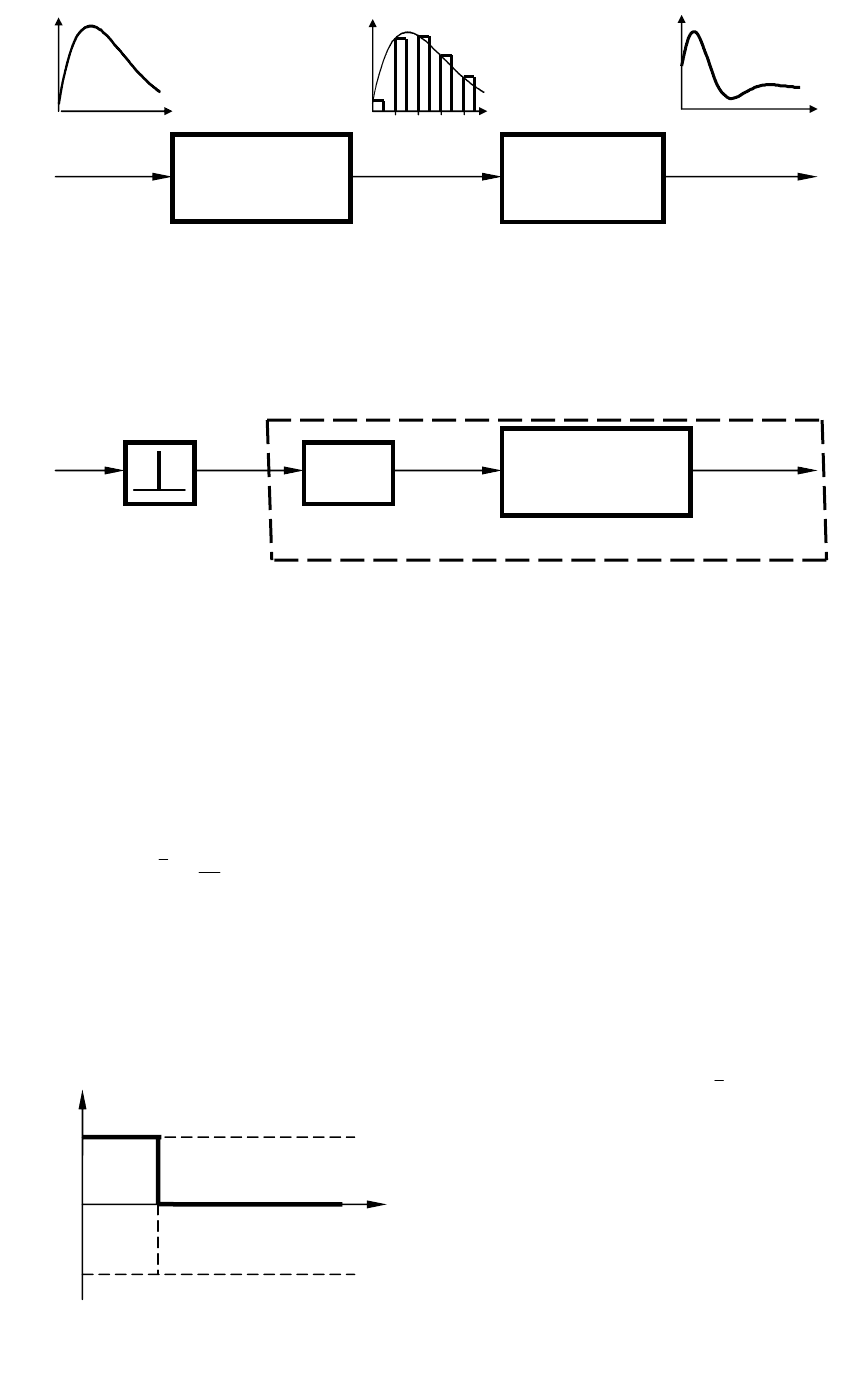
При осуществлении амплитудно-импульсной модуляции (АИМ)
импульсный элемент можно представить в виде последовательного
соединения идеального импульсного элемента ИИЭ и формирующе-
го элемента ФЭ (рис. 9.1, б). На выходе ИИЭ в моменты времени
n
T
t
= (или n
T
t
t
== ) производится решетчатая функции ][n
x
, зна-
чения которой пропорциональны значениям непрерывной функции
)(
t
x
в указанные моменты времени. Формирующий элемент харак-
теризуется тем, что вырабатывает на своем выходе из последователь-
ности мгновенных импульсов импульсы заданной формы.
При АИМ-1 на выходе форми-
рующего элемента при
n
t
= вос-
производятся прямоугольные им-
пульсы с амплитудой
и
k и длитель-
ностью
Tt γ
=
и
(рис. 9.2). Каждый
такой импульс можно представить
как сумму скачка
)(1
и
tk ⋅ при 0
=
t
и скачка
)(1
и
Ttk γ
−
⋅
при
T
t
γ
= с
обратным знаком, т.е.
)(
t
x
)(
м
tx
)(
t
y
а
0 1 2 3 4 5
Импульсный
элемент
Непрерыв-
ная часть
)(
t
x
][n
x
)(
м
tx
)(
t
y
ИИЭ Приведенная непрерывная часть
б
ФЭ
Непрерывная
часть
Рис. 9.1 Типовая структура разомкнутой САУ с АИМ
)(
м
tx
и
k
0
T
γ
t
и
k−
Рис.9.2. Прямоугольный
имп
у
льс
д
лительностью
T
γ

≥−−⋅
<
≤
⋅
=
. )](1)(1[
,0 )(1
)(
при
при
и
и
м
TtTttk
Tttk
Ttx
γγ
γ
Импульсная переходная характеристика такого формирующего
элемента описывается выражением
γ≥γ−−⋅
γ
<
≤
⋅
=
, )](1)(1[
,0 )(1
)(
при
при
и
и
tttk
ttk
tw
(9.1)
Передаточная функция формирующего элемента, определяемая
изображением импульсной переходной характеристики (9.1), может
быть найдена по теореме запаздывания [1 - 4] и будет равна
{}
q
e
ktwqW
q
γ
−
−
==
1
)()(
иф
L . (9.2)
где
pT
q = .
Формирующий элемент, передаточная функция которого описы-
вается формулой (9.2), называется
фиксатором (экстраполятором)
нулевого порядка, поскольку он фиксирует (продолжает) на интерва-
ле
γ
≤<
t
0 значение решетчатой функции ][n
x
.
При
1=γ
q
e
kqW
q
−
−
=
1
)(
иф
.
Если
1<<γ , то qe
q
γ−≈
γ
−
1 , отсюда
γ
≈
иф
)( kqW
. (9.3)
Формула (9.3) справедлива, если пренебречь влиянием конечной
длительности импульса и считать короткие прямоугольные импуль-
сы на выходе реального импульсного элемента эквивалентными по
своему действию на систему импульсов типа
δ
-функция. Для этого
обычно достаточно, чтобы в непрерывной части системы присутст-
вовало инерционное звено, постоянная времени которого превышает
длительность импульса.
Поскольку передаточные функции формирующего элемента и
непрерывной части описываются обычным преобразование Лапласа,
то их последовательное соединение принято называть
приведенной
