Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

)( ),(
21
qYqY – изображения выходных величин непрерывных участ-
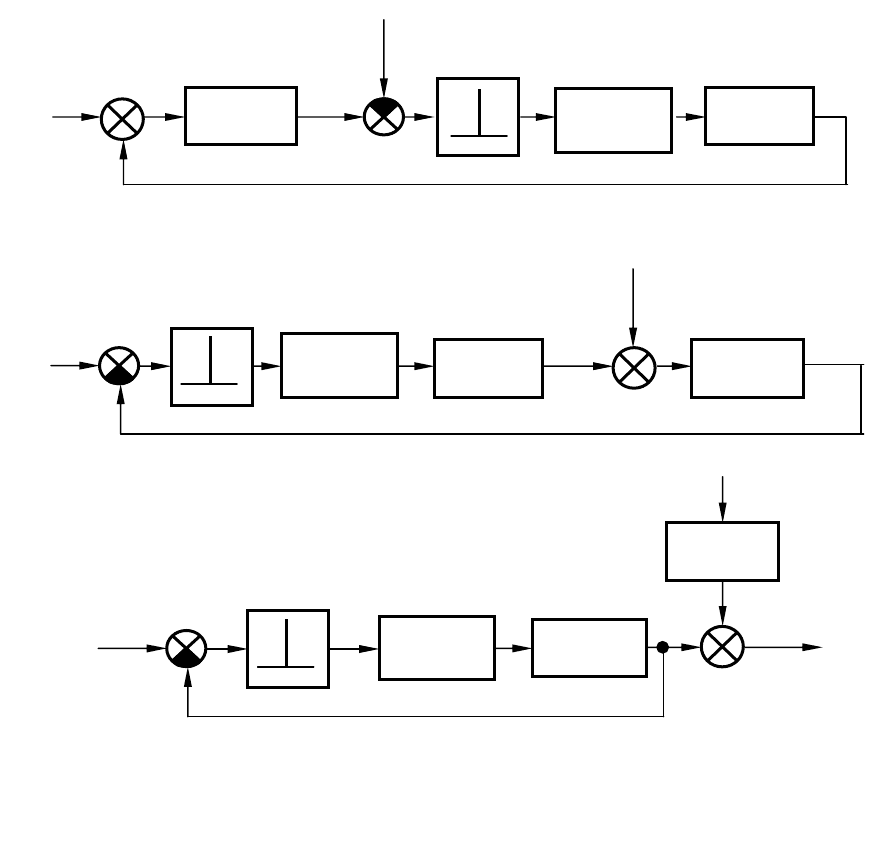
ков. Приведем эту структурную схему к простейшей форме.
Систему, изображенную на рис 9.5, а удобно представить в виде,
показанном на рис. 9.5, б. Для приведения воздействия
)(
2
qF к входу
импульсного элемента нужно определить реакцию соответствующего
непрерывного участка на это воздействие. На основании обычного
преобразования Лапласа изображение внешнего воздействия, приве-
денного к выходу второго непрерывного участка, равно
)()(
2
qFqW ⋅ . Поэтому систему, изображенную на рис. 9.5, б, можно
рассматривать как систему, приведенную на рис. 9.5, в, в которой
изображение эквивалентного внешнего воздействия
)()()()(
221
qFqWqFqF
⋅
−
=
.
)(
1
qF
)(
2
qF
)(
2
qY
)(
1
qY
а
)(
2
qW
)(
ф
qW
)(
1
qW
)(
2
qF
)(
1
qF
)(
1
qY
)(
2
qY
б
)(
2
qW
)(
ф
qW
)(
1
qW
)(
2
qF
)(q
F
)(q
Y
)(
2
qY
в
)(
2
qW
)(
ф
qW
)(
н
qW
Рис. 9.5. Приведение замкнутой импульсной САУ к
п
р
остейшей
ф
о
р
ме
(
ва
р
иант 1
)

Если обозначить изображение выходной величины через
)(q
Y
,
то, согласно рис. 9.5, в,
)()()()(
222
qFqWqYqY
⋅
+
=
.
При этом
)()()(
21н
qWqWqW
⋅
=
.
Рассмотрим замкнутую импульсную систему, в которой непре-
рывный элемент с передаточной функцией
)(
н
qW включен парал-
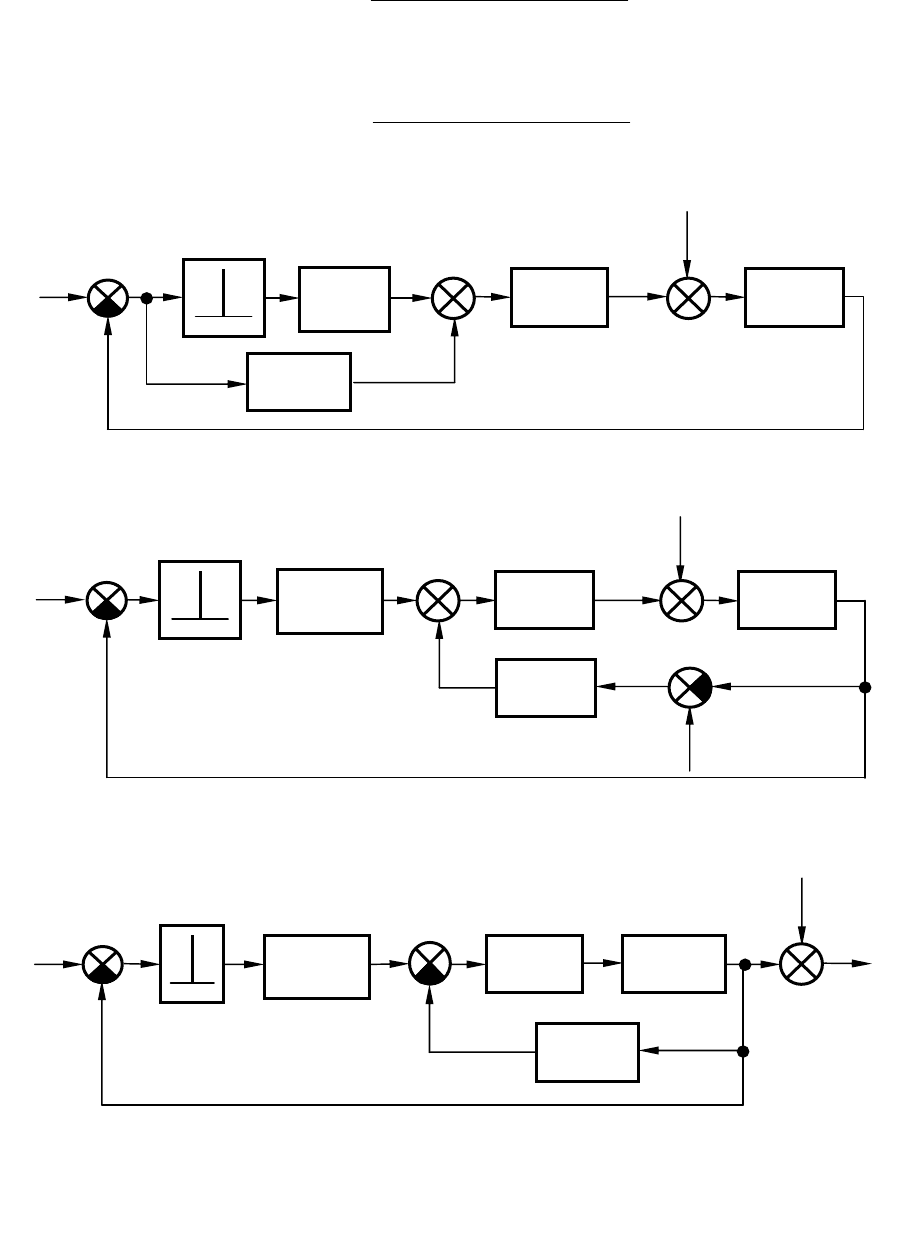
лельно импульсному элементу (рис. 9.6, а). Приведем эту систему к
простейшей форме.
Последовательные преобразования схемы, которые необходимо
применить, показаны на рис. 9.6, б, в. Рис. 9.6, б соответствует пере-
носу входа параллельного непрерывного элемента, а рис 9.6, в – при-
ведению внешних воздействий ко входу импульсного элемента. В
этом случае изображение приведенного внешнего воздействия равно
)(
)()()(1
)(
)(
)()()(1
1
)(
2
н21
2
1
н21
qF
qWqWqW
qW
qF
qWqWqW
qF
+
−
+
= .
При
0)(
1
≡qF
)(
)()()(1
)(
)(
2
T21
2
qF
qWqWqW
qW
qF
+
−= .
При
0)(
2
≡qF
)(
)()()(1
1
)(
1
н21
qF
qWqWqW
qF
+
=
.
Изображение
)(
2
qY связано с изображением )(q
Y
соотношени-
ем:
).(
)()()(1
)(
)(
)()()(1
)()()(
)()(
2
н21
2
1
н21
н21
2
qF
qWqWqW
qW
qF
qWqWqW
qWqWqW
qYqY
+
+
+
+
+=
При
0)(
1
≡qF
)(
)()()(1
)(
)()(
2
н21
2
2
qF
qWqWqW
qW
qYqY
+
+=
.
При
0)(
2
≡qF
)(
)()()(1
()()(
)()(
1
н21
н21
2
qF
qWqWqW
qWqWqW
qYqY
+
+= .
Таким образом, рассмотренные замкнутые импульсные системы
можно привести к простейшей форме (рис. 9.7), т.е. к системе, со-
)()(
1
qFqF −
)(
1
qF
)(q
Y
)(
2
qY
в
)(
н
qW
)(
ф
qW )(
1
qW )(
2
qW
)(
2
qF
)(
1
qF )(
1
qY
)(
2
qY
)(
1
qF
б
)(
н
qW
)(
ф
qW
)(
1
qW )(
2
qW
)(
2
qF
)(
1
qF
)(
1
qY
)(
2
qY
а
)(
н
qW
)(
ф
qW
)(
1
qW )(
2
qW
Рис. 9.6. Приведение замкнутой импульсной САУ к простейшей форме
(
ва
р
иант 2
)
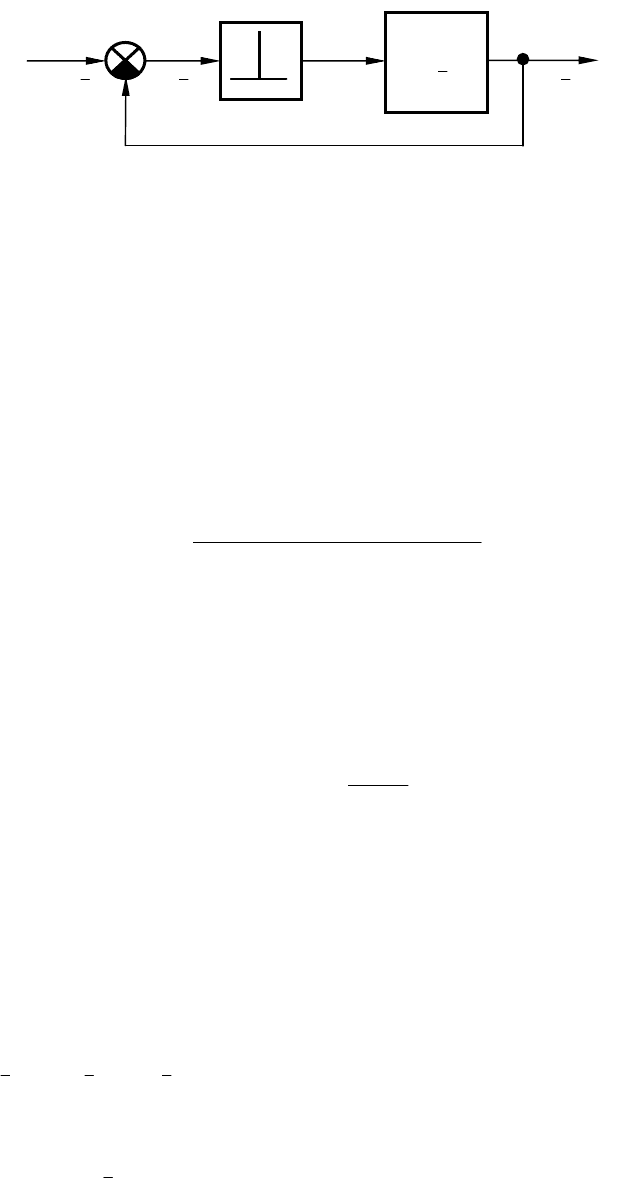
стоящей из идеального импульсного элемента и приведенной непре-
рывной части (ПНЧ), включающей формирующий элемент и непре-
рывную часть.
Передаточная функция приведенной непрерывной части нахо-
дится по правилам, изложенным в разделе 9.1. Так, например, для
САУ, приведенных на рис.9.5, 9.6, передаточные
функции ПНЧ будут
равны соответственно:
)()()()(
21пнч
qWqWqWqW
ф
⋅
⋅= - для САУ по рис. 9.5;
)()()(1
)()(
)()(
21
21
фпнч
qWqWqW
qWqW
qWqW
T
⋅⋅+
⋅
⋅= - для САУ по
рис. 9.6.
Если ПНЧ содержит только элементы с сосредоточенными пара-
метрами, то ее передаточная функция имеет вид рациональной дро-
би, т.е.
)(
)(
)(
пнч
qA
qB
qW
= ,
где
)(q
A
и )(qB – полиномы относительно q , причем для реальных
САУ степень полинома )(qB не превосходит степени полинома
)(q
A
.
В замкнутой импульсной системе (рис. 9.7) входная величина
импульсного элемента определяется соотношением
)()()(
t
y
t
f
t
x
−= .
Но импульсный элемент реагирует только на дискретные значе-
ния в моменты
n
t
=
, поэтому непрерывные функции можно заме-
нить решетчатыми, т.е.
)(q
F
)(q
X
)(q
Y
)(
t
f
)(
t
x
)(
t
y
Рис. 9.7. Простейшая форма замкнутой САУ с
АИМ
)(
)(
tw
q
W

]0,[]0 ,[]0 ,[ nyn
f
n
x
−=
. (9.15)
Получим уравнение импульсной САУ относительно изображе-
ний. Для этого подвергнем (9.15), например, дискретному преобразо-
ванию Лапласа. На основании теоремы линейности
)()0,()0,()0,(
****
qXqYqFqX =−= . (9.16)
С другой стороны (см. раздел 9.1), уравнение разомкнутой САУ с
АИМ относительно изображений может быть записано в виде
)(),(),(
**
p
*
qXqWqY ⋅ε=ε , (9.17)
где
{}
)(),(
пнч
*
p
qWqW D=ε – дискретная передаточная функция ра-
зомкнутой системы,
),( ),(
**
εqYqX – изображения решетчатых
функций
][n
x
и ] ,[ εny .
Полагая в уравнении (9.17)
0
=
ε
, получим изображение решет-
чатой функции
][n
y
:
)()()(
**
p
*
qXqWqY ⋅= . (9.18)
Уравнение (9.18) вместе с уравнением (9.16) описывает процессы
в замкнутой системе с АИМ в дискретные моменты времени
,...3,2,1== n
t
. Исключая из (9.16) и (9.18) переменную )(q
Y
, полу-
чим уравнение замкнутой САУ с АИМ относительно изображения
входной величины импульсного элемента:
)(
)(1
1
)(
*
*
p
*
qF
qW
qX
+
= . (9.19)
Оригинал этого изображения
][n
x
в САУ соответствует сигналу
ошибки или рассогласованию, поэтому уравнение (9.19) описывает
процессы в замкнутой системе с АИМ относительно сигнала ошибки
(рассогласования). Подставляя (9.19) в (9.17), получим уравнение
замкнутой импульсной системы в любой момент времени
)(
)(1
),(
),(
*
*
p
*
p
*
qF
qW
qW
qY
+
ε
=ε .
Отношение
)(
),(
),(
*
*
*
з
qF
qY
qW
ε
=ε
будет являться передаточной
функцией замкнутой САУ с АИМ. Следовательно, передаточная
функция замкнутой системы с АИМ описывается выражением
)(1
),(
),(
*
p
*
p
*
з
qW
qW
qW
+
ε
=ε
, (9.20)
где
),(
*
p
εqW , )(
*
p
qW – передаточные функции разомкнутой САУ и
АИМ при ненулевом и нулевом значениях смещения
ε.
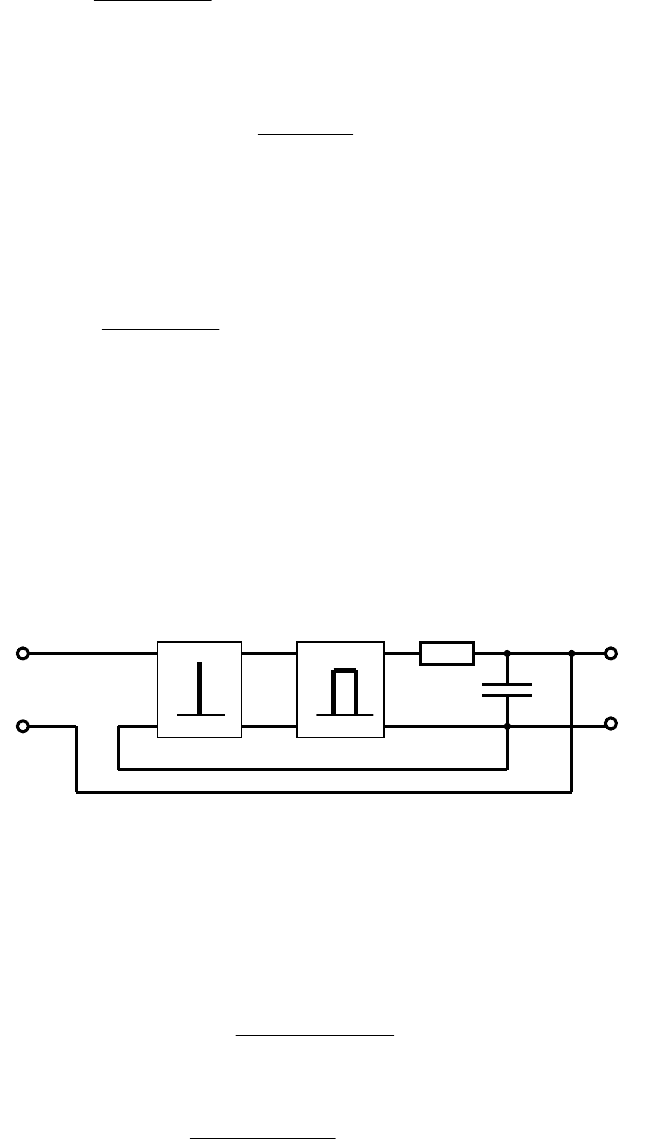
Пример 9.4. Получить передаточные функции для САУ с АИМ,
замкнутой единичной отрицательной обратной связью (рис. 9.8).
Передаточные функции такой разомкнутой системы были уже
получены в примере 9.1, т.е.
.1
)1(
, 0 1
),(
при
при
)(
и
)1(
и
*
p
≤ε<γ
−
−
γ≤ε≤
−
−
−
=ε
γ−εβ−
β−
βγ−
βε−
β−
χ−β−
e
ee
ee
k
e
ee
ee
k
qW
q
q
q
q
Для выражения
),(
*
p
εqW при
γ
≤
ε
≤
0 и при 0
=
ε
будем иметь:
ИИЭ ФЭ R
)(
t
f
)(
t
x
C
)(
t
y
Рис. 9.8. Пример замкнутой системы с АИМ

β−
β−
β
χ
−
−
= e
ee
e
kqW
q
1
)(
и
*
p
.
.
После подстановки этих выражений в формулу (9.20) получим
- при
γ
≤
ε
≤0
;
)]1(1[
)1()1(
1
1
1
),(
и
и
и
)1(
и
*
з
−−−
−−−
=
=
−
−
+
−
−
−
=ε
βγβ−
βε−βχβ−βε−
β−
β−
βγ
βε−
β−
χ−β−
ekee
eeeee
k
e
ee
e
k
e
ee
ee
k
qW
q
q
q
q
q
;
- при
1≤
ε
<γ
)]1(1[
)1(
1
1
)1(
),(
и
и
и
)(
и
*
з
−−−
−
=
−
−
+
−
−
=ε
βγβ−
βε−βχ
β−
β−
βγ
γ−εβ−
β−
β
γ
−
ekee
eee
k
e
ee
e
k
e
ee
ee
k
qW
q
q
q
q
q
.
Из приведенного примера видно, что передаточная функция
замкнутой импульсной системы представляет собой дробно-
рациональную функцию по
q
e , т.е.
)(
),(
),(
*
з
*
з
*
з
qA
qB
qW
ε
=ε
,
где
),(
*
з
εqB – числитель передаточной функции, а )(
*
з
qA – ее знаме-
натель. Знаменатель передаточной функции замкнутой САУ с АИМ
называется
характеристическим полиномом системы. Из приве-
денного примера видно, что характеристический полином системы
не зависит от величины относительной длительности импульса
γ :
)]1(1[)(
и
*
з
−−−=
βγ
β
−
ekeeqA
q
.

Аналогичные соотношения можно получить и для
Z
-
преобразования путем простой замены
z
e
q
=
. Тогда
)(
),(
)(1
),(
),(
*
з
*
з
*
p
*
p
*
з
zA
zB
zW
zW
zW
ε
=
+
ε
=ε
. (9.21)
Для рассмотренного примера
,1
)]1(1[
)1(
,0
)]1(1[
)1()1(
),(
при
при
и
и
и
и
*
з
≤ε<γ
−−−
−
γ≤ε≤
−−−
−−−
=ε
βγβ−
βε−βχ
βγβ−
βε−βχβ−βε−
ekez
zee
k
ekez
eeeze
k
zW
)]1(1[)(
и
*
з
−−−=
βγ
β
−
ekezzA .
В этом случае передаточные функции замкнутой САУ с АИМ яв-
ляются дробно-рациональными функциями относительно
z
.
9.3. Частотные характеристики систем с АИМ
Как уже отмечалось в разделе 8.2, изображение
)(* q
F
представ-
ляет собой периодическую функцию вдоль мнимой оси комплексной
плоскости
ω+σ
=
j
q с периодом
π
2 . Поэтому передаточные функ-
ции систем с АИМ будут также являться периодическими функция-
ми с периодом
π2 , т.е. для любого целого
r
будут иметь место соот-
ношения
),(),2(
*
p
*
p
ε=επ+ qWjrqW , ),(),2(
*
з
*
з
ε=επ+ qWjrqW . (9.22)
Амплитудно-фазовые частотные характеристики (АФЧХ) им-
пульсных систем получаются путем замены в передаточных функци-
ях параметра
q на ω
j
, где
T
ω
=
ω
– безразмерная относительная
частота. Поэтому, на основании (9.22) для АФЧХ систем с АИМ
справедливы соотношения
εω=επ+ω
εω=επ+ω
),,(),2(
),,(),2(
*
з
*
з
*
p
*
p
jWjrjW
jWjrjW
(9.23)
т.е., согласно (9.23),
частотные характеристики систем с АИМ
являются периодическими функциями относительной частоты
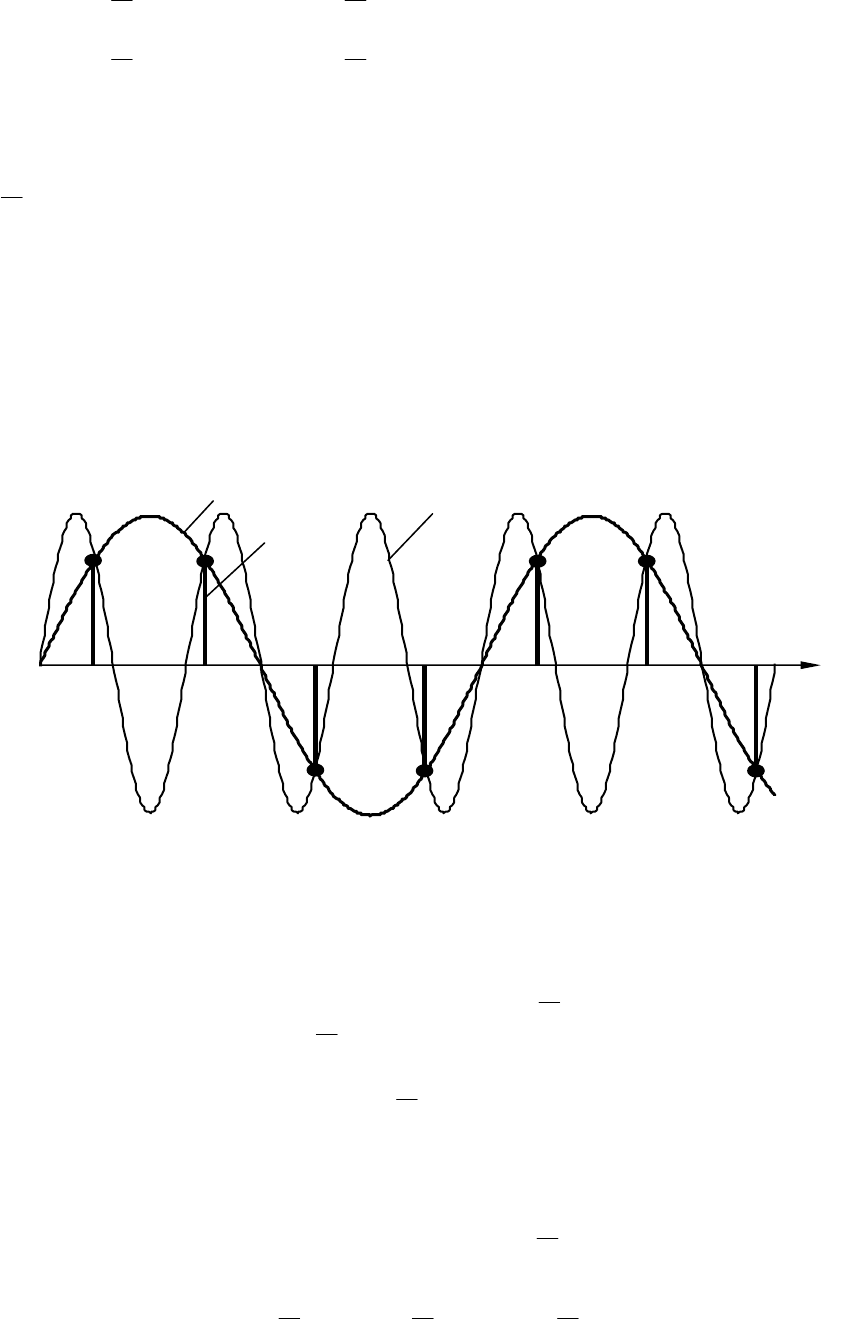
ω . Математически этот факт очевиден. Его физическое объяснение
заключается в следующем. Выходная величина импульсного элемен-
та, определяющая закон изменения импульсов, действующих на не-
прерывную часть, зависит только от значений входной величины в
дискретные моменты времени и не зависит от ее значений между
этими дискретами. Поэтому выходная переменная остается неизмен-
ной при гармонических входных переменных, относительная частота
которых отличается на
r
π
2 , где
r
– целое число (рис. 9.9).
Периодичность частотных характеристик является основным
свойством систем с АИМ, эти характеристики определены на интер-
вале изменения относительной частоты
ω
длительностью
π
2 .
Обычно принимают
π
≤
ω
<
π− .
Помимо этого, можно отметить и другие свойства.
9.3.1. Кроме зависимости от
ω
, частотные характеристики также
зависят от
ε
. Графически это выражается в виде серии кривых для
разных значений
ε. Обычно бывает достаточно одной характеристи-
ки при
0=ε .
9.3.2. Если представить, например,
),(
*
з
εωjW в виде
),(),(),(
*
з
*
з
*
з
εω+εω=εω jVUjW ,
ttf
ω
= sin)(
1
ttf
ω
=
3sin)(
2
][n
f
t
Рис. 9.9. Гармонические функции различных частот,
соответствующие одной и той же решетчатой функции
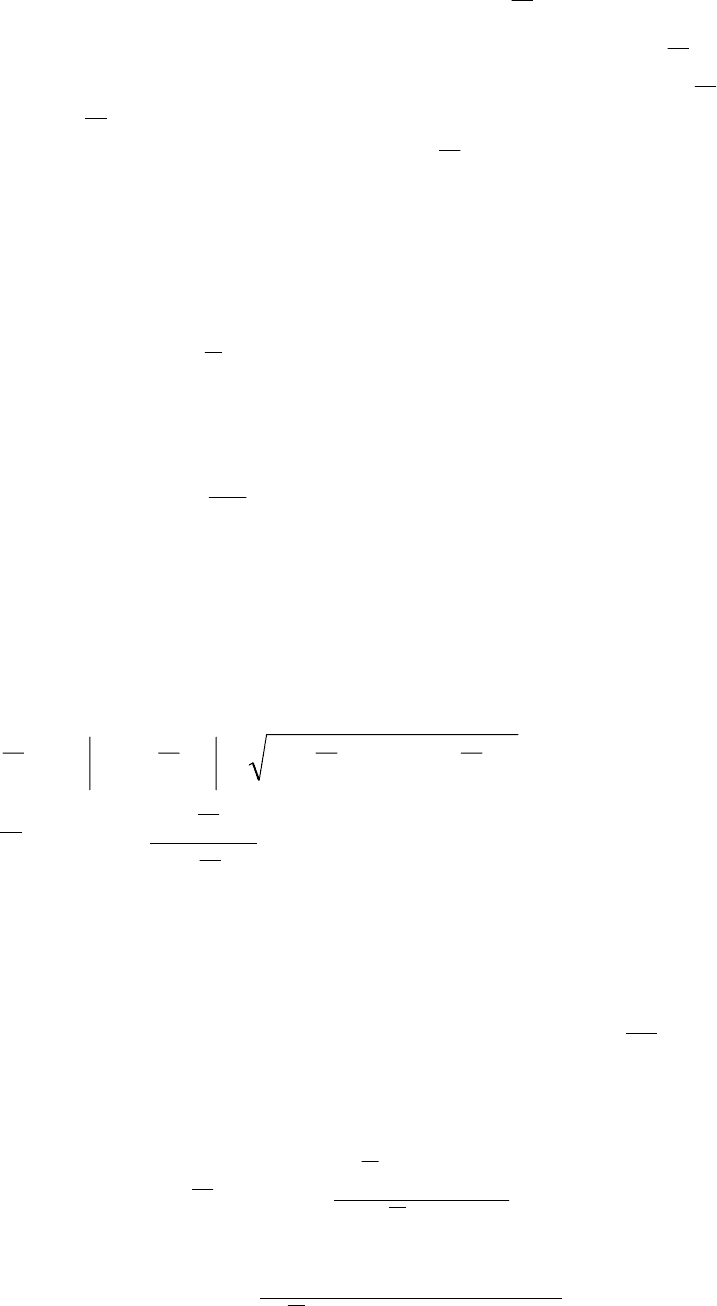
то вещественная частотная характеристика
),(
*
з
εωU будет четной
функцией частоты
ω
, а мнимая частотная характеристика ),(
*
з
εωU –
нечетной функцией. Поэтому достаточно принять изменение
ω
в
диапазоне
π≤ω
≤
0 .
9.3.3. В крайних точках интервала
π
≤
ω
≤
0 , АФЧХ принимает
значения
∑
∞
=
ε=ε
0n
*
з
] ,[),0( nfW и
∑
∞
=
ε−=επ
0n
*
з
] ,[)1(),( nfW
n
. Это
свойство вытекает из дискретного преобразования Фурье
nj
enfW
ω−
∞
=
∑
ε=επ
0n
*
] ,[),( .
9.3.4. При уменьшении периода квантования
T
(увеличении час-
тоты квантования
T
π
=ω
2
к
) частотные характеристики импульсных
систем приближаются к частотным характеристикам непрерывных
систем.
На основе перечисленных характеристик можно найти амплитуд-
ную и фазовую частотные характеристики САУ с АИМ. Например,
для замкнутой системы
),(),(),(),(
*
з
*
з
*
з
*
з
εω+εω=εω=εω jVUjWA , (9.24)
),(
),(
arctg),(
*
з
*
з
*
з
εω
εω
=εωϕ
U
V
. (9.25)
В качестве примера на рис. 9.10 показаны частотные характери-
стики разомкнутой (см. пример 9.1) и замкнутой (см. пример 9.4)
систем с АИМ для
8
и
=k , 05,0
0
=
T с, 01,0
=
T
с,
==β 2,0
0
T
T
,
5,0=
γ
и 0=ε . При этом АФЧХ описываются выражениями
,1)(
)1(
и
*
p
−
−
−=ω
β−ω
χ−β−ω
ee
ee
kjW
j
j
)]1(1[
)1(
),(
и
и
*
з
−−−
−
=ε
βγβ−ω
β
χ
β
−
ekee
ee
kqW
j
.
