Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

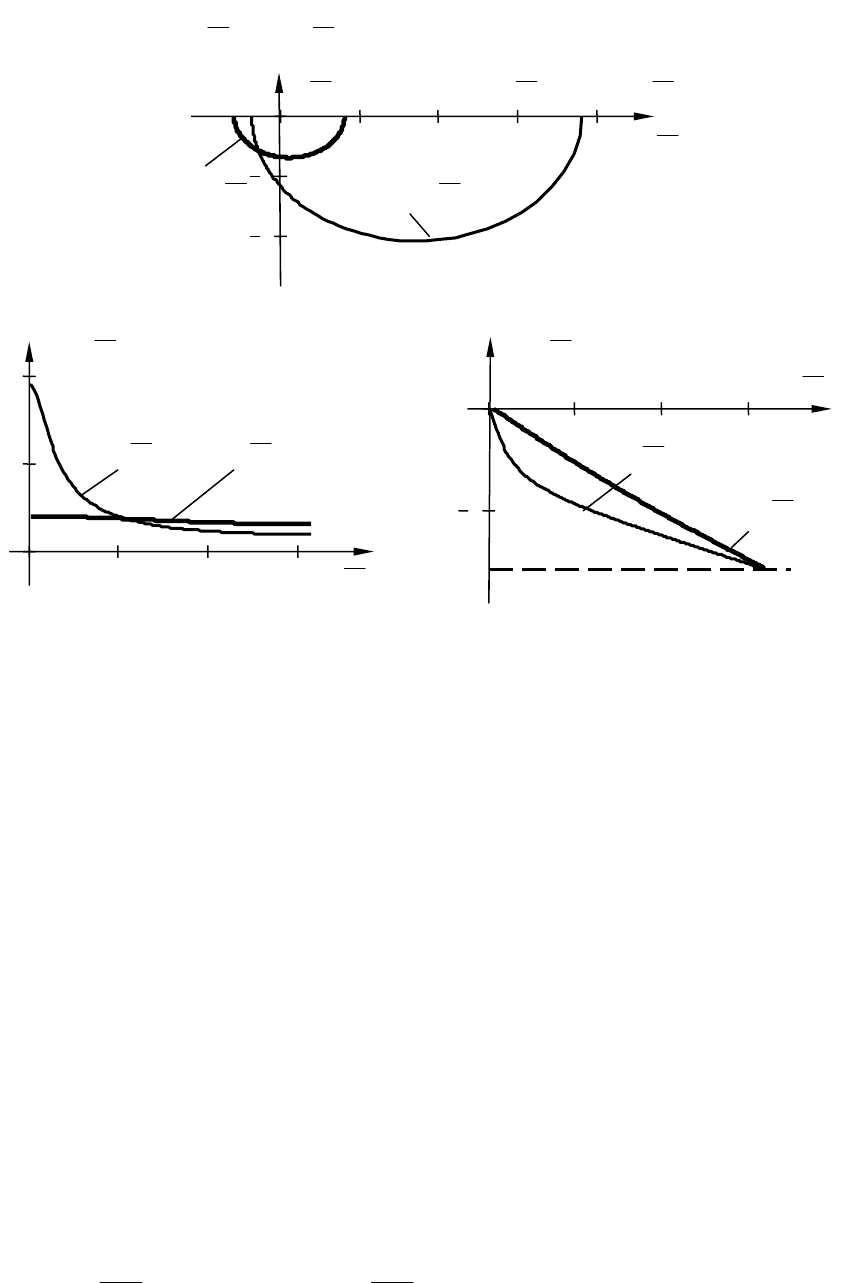
На рис. 9.10, а показаны годографы АФЧХ разомкнутой и замк-
нутой систем, они имеют вид полуокружностей. Также амплитудные
и фазовые частотные характеристики (рис. 9.10. б, в), рассчитанные
по формулам (9.24), (9.25).
10. УСТОЙЧИВОСТЬ СИСТЕМ С АИМ
10.1. Условия устойчивости систем с АИМ
Решетчатая функция ],[
ε
ny , определяющая закон изменения вы-
ходной величины в САУ с АИМ, в общем случае может быть найде-
на по формуле обращения
∫∫
∞
+
∞−
∞
+
∞−
⋅ε
π
=ε
π
=ε
jc
jc
qn
jc
jc
qn
dqeqFqW
j
dqeqY
j
ny )0,(),(
2
1
),(
2
1
] ,[
**
з
*
з
. (10.1)
)(
*
p
ωU , )(
*
з
ωU
0
=
ω
0
=
ω
)(
*
p
ωV
)(
*
з
ωU
)(
*
з
ωjW )(
*
p
ωjW
а
-1
0 1 2 3 4
2
1
)(
*
ωA
)(
*
p
ωA )(
*
з
ωA
ω
б
0 1 2 3
2
4
)(
*
ωϕ
ω
)(
*
p
ωϕ
)(
*
з
ωϕ
π
−
в
0 1 2 3
2
Рис. 9.10. Частотные характеристики разомкнутой и замкнутой
САУ с АИМ
Как было показано в разделе 8.1, интеграл в (10.1) может быть
вычислен через сумму вычетов от подынтегрального выражения. В
этом случае для любого воздействия
]0,[n
f
искомую величину
] ,[ εn
y
можно представить в виде
∑
=
ε+ε=ε
m
ii
nq
i
i
egnyny
~
в
)(] ,[] ,[
, (10.2)
где
nq
i
i
eg
~
)(ε – вычеты подынтегрального выражения в полюсах
i
q
~
передаточной функции замкнутой системы
),(
*
з
εqW , причем коэф-
фициенты
)(ε
i
g завися только от величины смещения ε; функция
] ,[
в
εny определяется подобным же образом через вычеты относи-
тельно полюсов изображения воздействия
)(
*
qF .
Величина
] ,[
в
εny представляет собой вынужденную состав-
ляющую переходного процесса и определяется видом внешнего воз-
действия
][n
f
.
Составляющая
∑
=
ε=ε
m
ii
nq
i
i
egny
~
п
)(] ,[ (10.3)
в (10.2) соответствует отклонению величины
],[
ε
ny от вынужденной
составляющей
] ,[
в
εny , определяет характер переходного процесса и
называется переходной составляющей.
Если с течением времени при
cons
t
=
ε
переходная составляю-
щая
] ,[
п
εny
стремится к нулю, т.е.
0] ,[lim
п
=ε
∞→
ny
n
, (10.4)
то система с АИМ называется устойчивой.
Если
∞
=ε
∞→
] ,[lim
п
ny
n
, то САУ будет неустойчивой, если
Cny
n
=
ε
∞→
] ,[lim
п
, где cons
t
=
C
, то САУ с АИМ называется ней-
тральной или находящейся на границе устойчивости.
Как видно из (10.2),
] ,[
п
ε
ny представляет собой сумму экспо-
ненциальных решетчатых функций с начальными значениями
)(
ε
i
g
и показателями nq
i
~
, где
i
q
~
– полюсы передаточной функции
)0,(
),(
),(
*
з
*
з
*
з
qA
qB
qW
ε
=ε
или нули ее характеристического полинома
)0,(
*
з
qA . Поэтому, если полюсы
i
q
~
передаточной функции замкну-
той системы будут иметь отрицательные вещественные части, то при
∞→n все слагаемые в (10.3) будут стремиться к нулю, условие
(10.4) будет выполняться и система будет устойчивой. Если хотя бы
один полюс передаточной функции замкнутой системы будет иметь
положительную вещественную часть, то соответствующее ему сла-
гаемое будет неограниченно нарастать, и система станет неустойчи-
вой. И, наконец, если хотя бы один из полюсов будет иметь вещест-
венную часть, равную нулю, а вещественные части остальных полю-
сов будут отрицательными, то система будет находиться на границе
устойчивости.
Таким образом, для того чтобы САУ с АИМ была устойчива,
необходимо и достаточно, чтобы все полюсы ее передаточной
функции имели отрицательные вещественные части, т.е. распо-
лагались в левой части полосы
π
≤
<
π
−
qIm комплексной плоско-
сти
q .
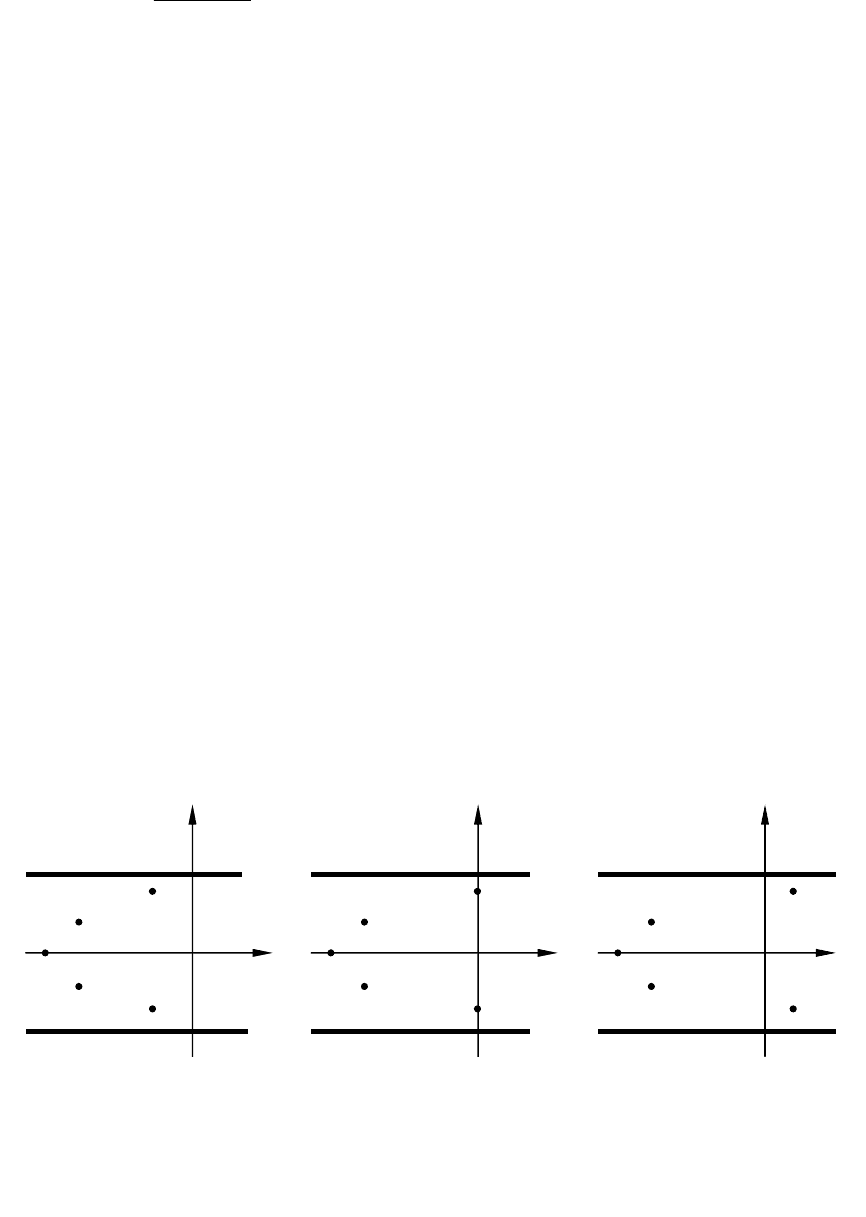
Это условие иллюстрирует рис. 10.1. Для устойчивой системы
полюсы
51
qq − располагаются слева от мнимой оси qIm (рис. 10.1,
а). Если полюсы
54
, qq лежат на мнимой оси (рис. 10.1, б), то САУ
находится на границе устойчивости. Расположение полюсов
54
, qq
справа от мнимой оси соответствует неустойчивой системе.
Таким образом, если для описания САУ с АИМ применено дис-
кретное преобразование Лапласа, то необходимое и достаточное ус-
qIm
π
4
q
1
q
3
q qRe
2
q
0
5
q
π−
а
qIm
π
4
q
1
q
3
q qRe
2
q
0
5
q
π
−
б
qIm
π
4
q
1
q
3
q qRe
2
q
0
5
q
π−
в
Рис. 10.1. Расположение полюсов на комплексной плоскости для
устойчивой САУ (а), САУ на границе устойчивости (б) и
неустойчивой САУ (в)
ловие ее устойчивости аналогично такому же условию для линейных
непрерывных систем. Отличие заключается только в том, что из-за
периодичности передаточной функции САУ с АИМ все ее полюсы
располагаются внутри полосы
π
≤
<
π
−
qIm .
Необходимое и достаточное условие устойчивости САУ с АИМ
изменяется, если для описания системы применено модифицирован-
ное
Z
-преобразование. При
z
e
q
=
передаточная функция замкнутой
системы принимает вид
)(
),(
),(
*
з
*
з
*
з
zA
zB
zW
ε
=ε
, где
)()()()(),(
01
1
1
*
з
ε+ε+⋅⋅⋅+ε+ε=ε
−
−
bzbzbzbzB
k
k
k
k
,
01
1
1
*
з
)( azazazazA
m
m
m
m
++⋅⋅⋅++=
−
−
,
причем
m
k
≤ .
Преобразование
z
e
q
=
отображает полосу
π
≤
<
π
−
qIm
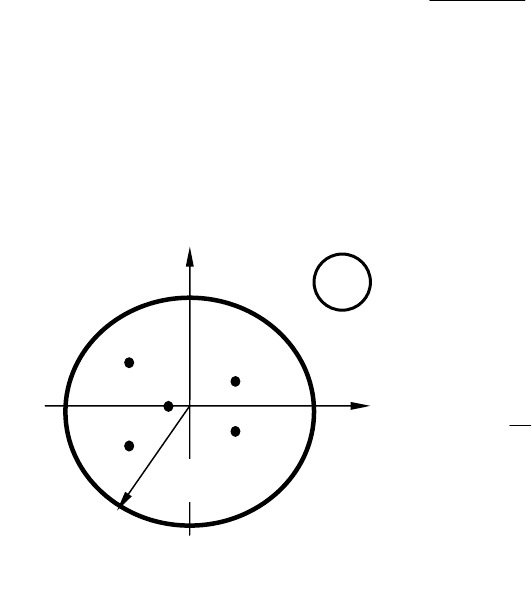
(рис. 10.1) на всю
плоскость
z
, причем отрезок
мнимой оси
)Im(qjjq
=
ω
=
отображается в
окружность единичного радиуса
с центром в начале координат
(рис. 10.2). Поэтому для устой-
чивой САУ с АИМ необходимо
и достаточно, чтобы все полюсы
i
z передаточной функции ),(
*
з
εzW располагались бы внутри
круга единичного радиуса
1||
<
z
, а окружность 1|| =
z
будет яв-
ляться границей устойчивости. Это обстоятельство некоторым обра-
зом изменяет подход к исследованию устойчивости систем с АИМ.
10.2. Анализ устойчивости систем с АИМ
Для анализа устойчивости САУ с АИМ удобно применять анало-
ги критериев устойчивости, известных из теории непрерывных сис-
тем. Применение каждого из этих аналогов в определенных случаях
может оказаться предпочтительным.
z
Im
-
zRe
Рис.10.2. Область устойчивости
САУ с АИМ на плоскости
z
z
1
z
3
z
4
z
2
z
5
z
R =1
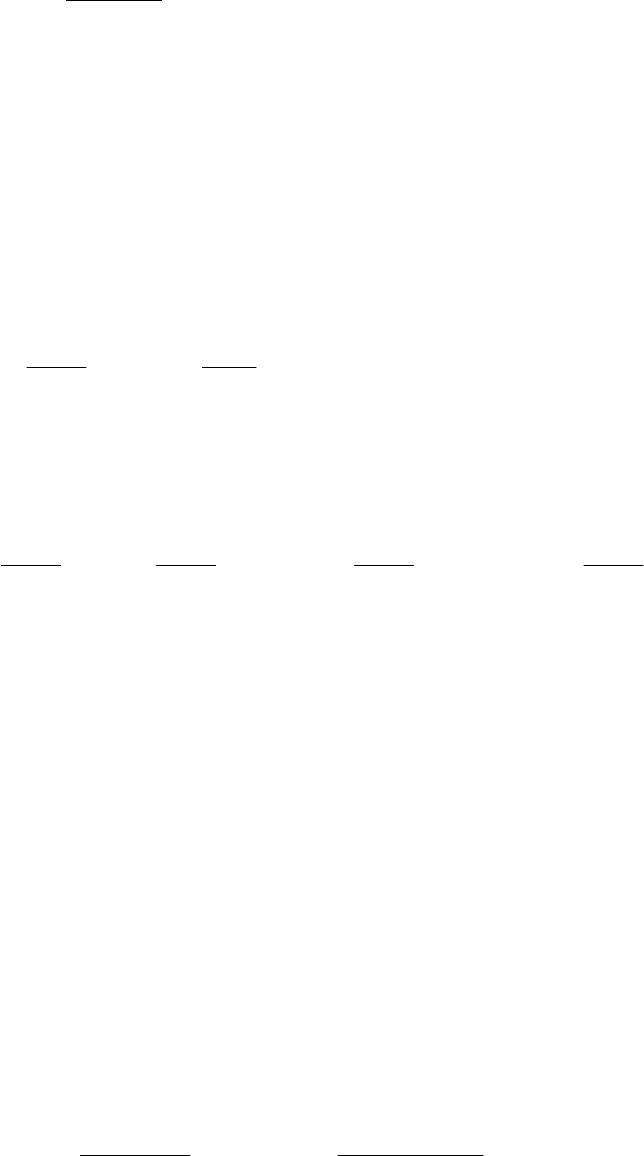
10.2.1. Аналог критерия Гурвица
Пусть замкнутая система описана передаточной функцией вида
)(
),(
),(
*
з
*
з
*
з
zA
zB
zW
ε
=ε
, где
01
1
1
*
з
)( azazazazA
m
m
m
m
++⋅⋅⋅++=
−
−
–
ее характеристический полином. Как было показано в предыдущем
разделе, САУ будет устойчива, если корни
i
z
(
)
mi .. ,.2 ,1
=
уравне-
ния
0)(
*
з
=zA будут располагаться внутри круга 1|| <
z
. В этом слу-
чае критерий Гурвица напрямую применять нельзя, т.к., в соответст-
вии с его формулировкой, корни характеристического уравнения
должны располагаться в левой комплексной полуплоскости.
Произведем замену
1
1
−
+
=
w
w
z
или
1
1
−
+
=
z
z
w
, (10.5)
тогда характеристическое уравнение
0)(
*
з
=zA примет вид
0
1
1
1
1
1
1
1
1
01
1
1
*
з
=+
−
+
+⋅⋅⋅+
−
+
+
−
+
=
−
+
−
−
a
w
w
a
w
w
a
w
w
a
w
w
A
m
m
m
m
,
или
0
01
1
1
=++⋅⋅⋅++
−
−
cwcwcwc
m
m
m
m
,
(10.6)
где
i
c
()
mi .. ,.2 ,1= – коэффициенты уравнения
(
)
0
*
з
=wA , причем
,)1(
1 1
)1(
2211
1
0
−+
−
−
−+
+
⋅⋅⋅+
−
−
+
−
−
−
−
=
−
=
∑
j
iim
k
i
j
imi
j
imi
j
im
ac
ii
m
i
ij
где
)!(
)!(
,
)!(
!
jimj
im
j
im
−−
−
=
−
λ−αλ
α
=
λ
α
– биномиальные коэф-
фициенты.
Подстановка (10.5) называется
W
- преобразованием, оно преоб-
разует круг единичного радиуса комплексной плоскости
z (рис. 10.3,
а) в левую часть комплексной плоскости
w (рис. 10.3, б). Корни
уравнения
0)(
*
з
=zA , лежащие внутри круга единичного радиуса
комплексной плоскости
z , будут соответствовать корням уравнения
()
0
*
з
=wA , лежащим в левой части комплексной плоскости w .
Таким образом, замкнутая система с АИМ будет устойчива,
если выполнены неравенства Гурвица
0>
j
c
()
mj ..., ,2 ,1 ,0= , 0>
∆
k
(
)
1 ,.... ,2 ,1 −
=
mk
где
k
∆ – определители, образуемые вычеркиванием
k
строк и
столбцов в таблице (миноры определителя Гурвица)
Граница устойчивости определяется теми значениями парамет-
ров, при которых определитель Гурвица обращается в нуль, т.е. при
0
10
=
∆
=
∆
−
mm
c
или при
0
0
=c , 0
1
=
∆
−m
. (10.7)
z
Im
1− 1
z
Re
а
z
wIm
0
wRe
б
w
Рис. 10.3.
W
- преобразование
1
∆
⋅ ⋅⋅
−−−
531
mmm
ccc
2
∆
42
⋅ ⋅⋅
−−
mmm
ccc
3
∆
0
31
⋅
⋅
⋅
−−
mm
cc
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Рассмотрим некоторые частные случаи
Для
1=m , т.е. если
01
*
з
)( azazA += ,
01
*
з
)( cwcwA += , причем
011
aac += ,
010
aac −= , условия устойчивости САУ с АИМ будут
иметь вид
>−
>+
.0
,0
01
01
aa
aa
(10.8)
Для
2=m , т.е. если
01
2
2
*
з
)( azazazA ++= ,
01
2
2
*
з
)( cwcwcwA ++= ,
0122
aaac
+
+
=
,
()
021
2 aac −= ,
2100
aaac +−=
. Условия устойчивости:
>+−
>−
>++
.0
,0
,0
210
02
012
aaa
aa
aaa
(10.9)
Для
3=m , т.е. если
01
2
2
3
3
*
з
)( azazazazA +++= ,
01
2
2
3
3
*
з
)( cwcwcwcwA +++= , тогда
01233
aaaac
+
+
+
=
,
(
)
12032
3 aaaac
−
+
−
= ,
(
)
12031
3 aaaac
−
−
+
= .
01230
aaaac
−
+
−
= .
Условия устойчивости:
>−−−
>−+−
>+++
.0)()(
,0
,0
200133
0123
0123
aaaaaa
aaaa
aaaa
(10.10)
Пример 10.1. Определить устойчивость, найти граничный коэф-
фициент передачи и построить границу устойчивости для системы,

изображенной на рис. 9.8, при следующих ее параметрах: 25
и
=k ,
05,0
0
=T с, 01,0=
T
с,
==β 2,0
0
T
T
, 5,0
=
γ
.
Согласно ранее рассмотренному примеру 9.4, характеристиче-
ский полином системы, приведенной на рис. 9.8, имеет вид
01и
*
з
)]1(1[)( azaekezzA +=−−−=
βγβ−
,
где
1
1
=a ,
334,1)]1(1[
и0
=−−−=
β
γ
β
−
ekea .
Поскольку порядок системы 1
=
m , то воспользуемся условиями
устойчивости (10.8):
<−=−=−
>
=
+
=
+
.0334,0334,11
,0334,2334,11
01
01
aa
aa
Так как второе условие не выполняется, то заданная система с
АИМ неустойчива.
Получим расчетное выражение для граничного значения коэф-
фициента передачи
гри,
k
из условия
=
−=
010
aac
{
}
0)]1(1[1
гри,
=−−−−=
β
γ
β−
eke , отсюда
)1(
1
),(
гри,
−
+
=γβ
βγβ−
β
−
ee
e
k
. (10.11)
При 2,0=
β
, 5,0=
γ
25122,21
игри,
=
<
=
kk
, что подтверждает
неустойчивость системы при заданных параметрах.
На рис. 10.4 по формуле (10.11) построена граница устойчи-
вости САУ
)(
гри,
γ
= fk
(рис. 10.5, а) при 2,0cons
t
==
β
и
)(
гри,
β= fk (рис. 10.4, б) при 5,0const
=
=
γ
. При 0=
γ
(выработ-
ке на выходе импульсного элемента мгновенных импульсов) гранич-
ный коэффициент передачи неограниченно нарастает, а при
1=
γ
он
имеет минимальное значение
033,10
гри,
=
k . С увеличением
β
(рис. 10.4, б), т.е. при приближении постоянной времени инерцион-
ного звена
0
T к периоду квантования
T
, величина
гри,
k также
уменьшается, а при 0→
β
неограниченно возрастает. Область ус-
тойчивости САУ расположена ниже кривых
|
2,0
гри,
)(
=β
γ= fk и
|
5,0
гри,
)(
=γ
β= fk .
10.2.2. Аналог критерия Михайлова
При исследовании устойчивости САУ с АИМ с помощью анало-
га критерия Михайлова в характеристическом полиноме
01
)1(
1
*
з
)( aeaeaeaqA
qqm
m
mq
m
++⋅⋅⋅++=
−
−
)(
гри,
γ
= fk
γ
а
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
60
120
180
240
300
)(
гри,
β= fk
β
б
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
75
150
225
300
Рис. 10.4. Граница устойчивости САУ
)(
гри,
γ
=
fk
(а) и
)(
гри,
β
=
fk
(б)
производят замену оператора дискретного преобразования Лапласа
q на переменную ω
j
и на комплексной плоскости строят характе-
ристическую кривую
).()(
)(
01
)1(
1
*
з
ω+ω=
=++⋅⋅⋅++=ω
ω
−
ω
−
ω
jjVU
aeaeaeajA
jmj
m
mj
m
(10.12)
Замкнутая система с АИМ будет устойчива, если при возраста-
нии
ω от
π
− до π число полных оборотов вектора кривой )(
*
з
ωjA
в положительном направлении (против часовой стрелки) равно сте-
пени характеристического полинома.
В силу симметрии характеристической кривой )(
*
з
ωjA при
0<ω≤π− и π≤ω≤0 относительно вещественной оси, при по-
строении
)(
*
з
ωjA можно ограничиться интервалом положительных
изменений
ω . При этом число оборотов, совершаемых вектором
)(
*
з
ωjA , уменьшится вдвое и аналог критерия Михайлова можно
сформулировать следующим образом.
Замкнутая система с АИМ будет устойчива, если при воз-
растании
ω от 0 до
π
характеристическая кривая )(
*
з
ωjA об-
ходит последовательно в положительном направлении
m2
квад-
рантов комплексной плоскости, где
m – степень характеристи-
ческого полинома.
Ни рис. 10.5, а приведен вид характеристических кривых
)(
*
з
ωjA , соответствующих устойчивым замкнутым системам с АИМ
при
3 ,2 ,1=m , а на рис. 10.5, б – вид характеристических кривых для
неустойчивых систем с таким же порядком. Легко видеть, что для
неустойчивых САУ количество обходимых квадрантов
m
k
2≠
(при
21 1 ≠==
k
m , при 43 2
≠
=
=
k
m , при 64 3 ≠
=
=
k
m ).
Характеристическая кривая весьма просто может быть построена
геометрически. При заданном значении
1
ω
=
ω
вектор )(
*
з
ωjA пред-
ставляет собой диагональ многоугольника, стороны которого равны
коэффициентам
m
aaa ..., , ,
10
и образуют между собой равные углы
1
ω−π
. При 0=
ω
011
*
з
)0( aaaaA
mm
++⋅⋅⋅++=
−
.
При
π
=ω
