Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления

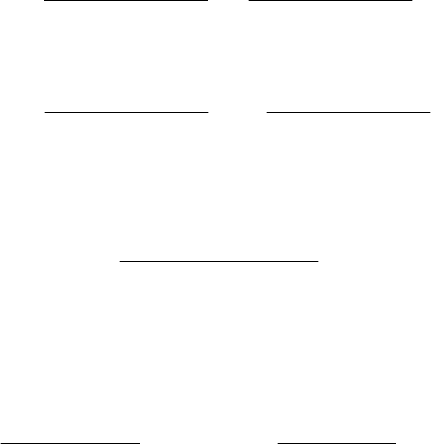
Уравнение статики (г), как видим, полностью соответствует

обобщенному уравнению (5.3), отличаясь лишь обозначениями.

Подставим в уравнение (г) заданные значения величин и опреде-

лим максимальное

maxн,

U

и минимальное

minн,

U

значение выход-

ного напряжения, соответствующие соответственно минимальному

1

minн,

=I

А и максимальному

10

maxн,

=

I

А токам нагрузки:

6,16

1,0105,01

1,0

1

1,0105,01

105,0

5

maxн,

=

⋅⋅+

−

⋅⋅+

⋅

=U

В;

16

1,0105,01

1,0

10

1,0105,01

105,0

5

minн,

=

⋅⋅+

−

⋅⋅+

⋅

=U

В.

Представим выходное напряжение в форме (5.6):

3,16

2

minн,maxн,

омн,

=

+

=

UU

U

н

В;

6,0

minн,maxн,н

=

−

=

∆ UUU В;

84,1

3,162

%1006,0%100

омн,омн,

омн,

н

омн,н

±=

⋅

±=

⋅∆

±=

нн

н

UU

U

UU

%.

Таким образом, при изменении в оговоренном диапазоне возму-

щающего воздействия (тока нагрузки) отклонение выходного напря-

жения не превысит величины

±1,84% от номинального значения.

5.2. Показатели качества в динамических режимах

работы САУ

Основными показателями, характеризующими работу САУ в ди-

намических режимах, являются время переходного процесса и пере-

регулирование. Напрямую их можно определить непосредственно по

переходной характеристике САУ, приведенной на рис. 5.4.

Время переходного процесса

пп

t характеризует быстродействие

системы. Определяется как интервал времени от начала переходного

процесса до момента, когда отклонение выходной величины от ее

нового установившегося значения

уст

h становится меньше опреде-

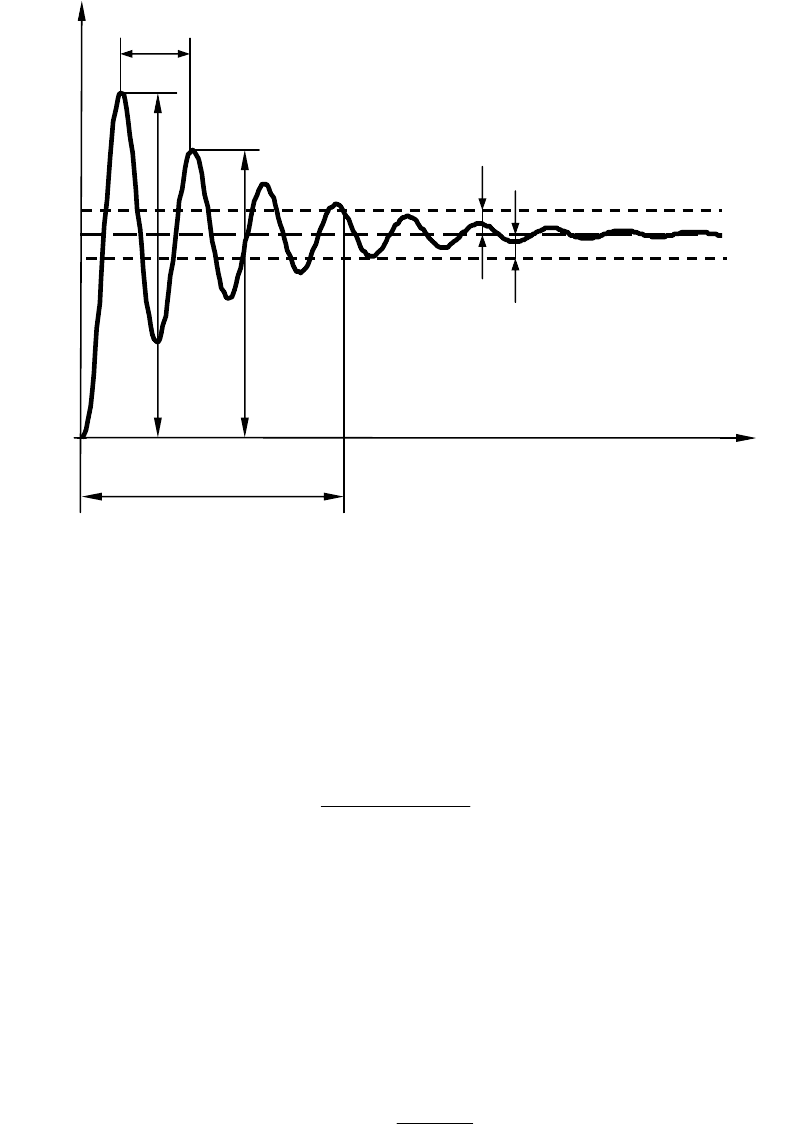
ленной достаточно малой величины. На рис 5.4. эта величина обо-

значена как

∆. Для общепромышленных систем обычно принимается

уст

05,0 h⋅=∆ , т.е. 5% от установившегося значения.

Перерегулированием

σ

называется максимальное отклонение

выходной величины

1max

h на интервале переходного процесса от ус-

тановившегося после окончания переходного процесса

уст

h , выра-

женное в процентах:

100

уст

уст1max

⋅

−

=σ

h

hh

%.

Дополнительными показателями качества принято считать коле-

бательность и период собственных колебаний.

Колебательность

µ

характеризует степень затухания переход-

ного процесса и обычно определяется отношением соседних макси-

мумов на переходной характеристике,

2max

1max

h

=µ

,

т.е. чем больше

µ

, тем быстрее затухает переходный процесс. В за-

висимости от характера затухания различают следующие типы пере-

)(

t

h

к

T

∆

уст

h

∆

1max

h

2max

h

0

t

пп

t

Рис 5.4. Определение показателей качества в динамике САУ

ходных характеристик: монотонная (нет ни одного колебания), апе-

риодическая (не более одного колебания) и колебательная (несколько

колебаний).

Период собственных колебаний

к

T определен минимальным

значением мнимой части корней характеристического уравнения

0)( =

p

A

. На рис. 5.4 он показан как расстояние между соседними

максимумами переходной характеристики САУ.

5.3. Косвенные методы оценки качества переход-

ного процесса

Исчерпывающее представление о качестве переходного процесса

дает, конечно, сама переходная характеристика. Однако при разра-

ботке САУ необходимо иметь возможность судить об основных по-

казателях качества переходного процесса без построения переходных

характеристик, по каким-либо косвенным признакам, которые опре-

деляются более просто и позволяют связать показатели качества с

параметрами САУ. Такие признаки называются

критериями каче-

ства

переходного процесса.

Существуют три группы критериев качества: частотные, корне-

вые и интегральные.

5.3.1. Частотные критерии оценки качества

Наибольшее распространения получили частотные критерии, в

основу которых положено использование частотных характеристик

САУ. Для иллюстрации возможности оценки качества переходного

процесса по частотным характеристикам установим точную аналити-

ческую зависимость между переходной характеристикой

)(

t

h

и час-

тотными характеристиками САУ (ВЧХ, АЧХ, ЛАЧХ и т.д.).

В качестве примера рассмотрим связь переходных характеристик

САУ с вещественной частотной характеристикой

)(

ω

P .

Пусть на вход устойчивой САУ, передаточная функция которой

)( pW

не содержит полюсов в правой полуплоскости, подано еди-

ничное ступенчатое воздействие

)(1

t

. Из этого следует, что импульс-

ная переходная функция

)(

t

w удовлетворяет условию абсолютной

интегрируемости и может быть вычислена с помощью обратного

преобразования Фурье по формуле

∫∫

∞

−

∞

−

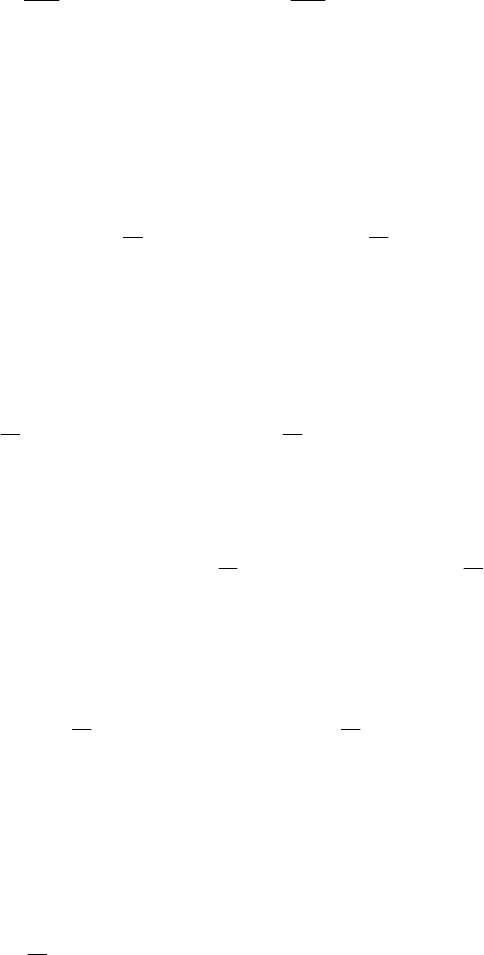
ω

ωω+ωω

π

=ωω

π

= dtjtjWdejWtw

tj

)sin)(cos(

2

1

)(

2

1

)(

.

Если вещественная часть

)(

ω

P

функции )(

ω

jW – четная функ-

ция а мнимая часть

)(ωQ – нечетная функция, то получим

∫∫

∞

ωωω

π

−ωωω

π

=

00

sin)(

1

cos)(

1

)( tdQtdPtw .

Т.к. при

0

<

t

оригинал равен нулю и 0)(

=

−

t

w , то

.0sin)(

1

cos)(

1

)sin()(

1

)cos()(

1

)(

00

=ωωω

π

+ωωω

π

=

=ωω−ω

π

−ωω−ω

π

=−

∫∫

∞∞

∞

tdQtdP

dtQdtPtw

или

∫∫

∞

ωωω

π

−=ωωω

π

00

sin)(

1

cos)(

1

tdQtdP .

В окончательном виде оригинал запишется соотношением

∫

∞

ωωω

π

=

0

cos)(

2

)( tdPtw . (5.7)

Поскольку переходная функция САУ является интегралом от им-

пульсной переходной функции, т.е.

∫

=

t

dttwth

0

)()( , то связь между

переходной характеристикой САУ и ее ВЧХ находится путем под-

становки формулы (5.7) в соотношение между двумя временными

характеристиками:

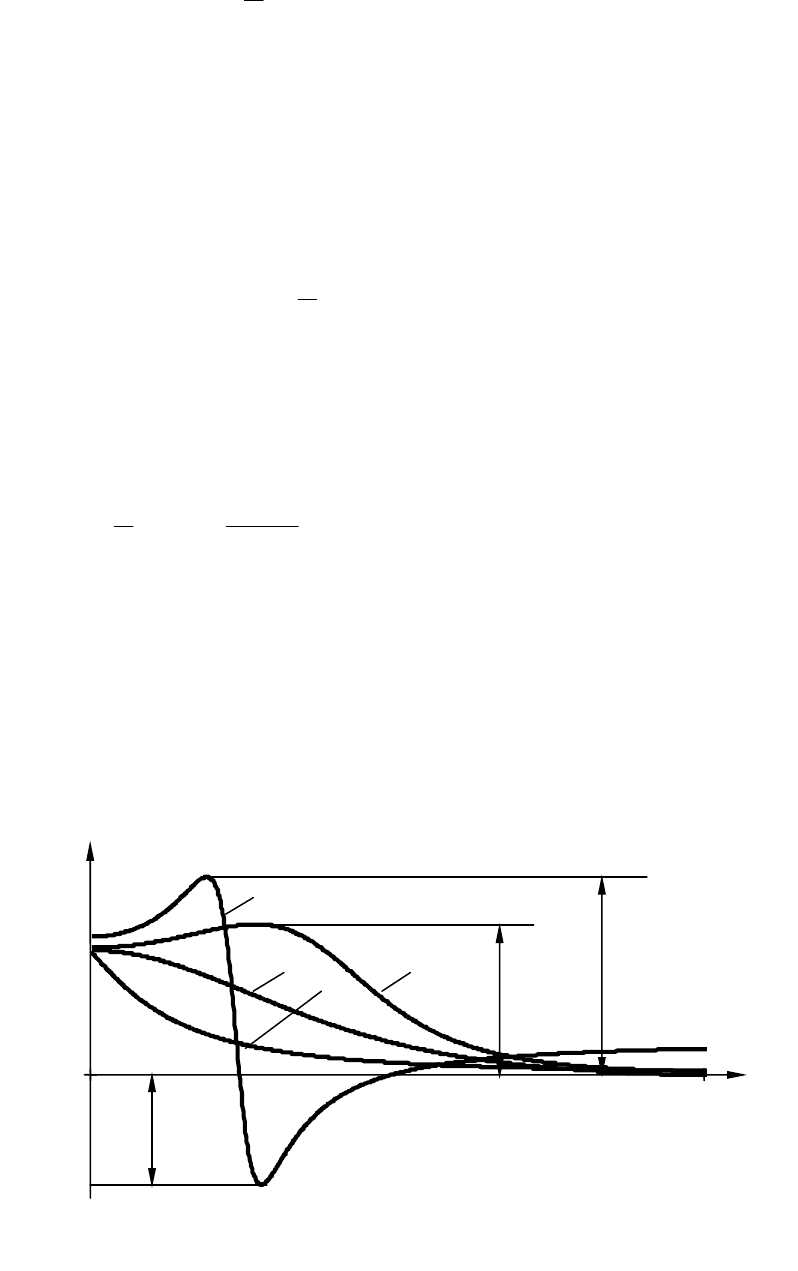
dttdPdttwth

tt

∫∫∫













ωωω

π

==

∞

000

cos)(

2

)()( . (5.8)

Формула (5.8) представляет собой запись интеграла Фурье для

четной функции в вещественной форме, поэтому, ввиду абсолютной

интегрируемости функции

)(

t

w можно изменить порядок

интегрирования:

ω













ωω

π

=

∫∫

∞

dtdtPth

t

00

cos)(

2

)( .

После вычисления внутреннего интеграла окончательно получим:

ω

π

=

∫

d

t

Pth

t

0

sin

)(

2

)(

. (5.9)

Пользуясь формулой (5.9) можно непосредственно или

приближенно [4, 5] по ВЧХ замкнутой САУ рассчитать ее переход-

ную характеристику. Также можно составить предварительное

приближенное суждение и о качестве по виду ВЧХ. Различные виды

ВЧХ представлены на рис. 5.5.

)(ω

P

4

)0(P

2 1 3

1max

P

2max

P

0

ω

mi

n

P

Рис. 5.5. Типы вещественных частотных характеристик САУ

Основные положения оценки качества переходного процесса по

ВЧХ сводятся к следующему:

5.3.1.1. Установившееся значение

)(

уст

∞

=

hh переходной харак-

теристики определяется начальным значением ВЧХ

)0(

уст

Ph = . На-

чальное значение

)0(

нач

hh = определяется конечным значением

ВЧХ

)(

нач

∞= Ph

.

5.3.1.2. Двум ВЧХ, сходным по форме, но отличающимся мас-

штабом по оси абсцисс в

n раз, соответствуют переходные характе-

ристики, сходные по форме, но отличающиеся масштабом по оси

абсцисс в

n

1

раз. Двум ВЧХ, сходным по форме, но отличающимся

масштабом по оси ординат в m раз, соответствуют переходные ха-

рактеристики, также сходные по форме, но отличающиеся масшта-

бом по оси ординат в

m раз.

5.3.1.3. Разрыв непрерывности на ВЧХ свидетельствует о том,

что система находится на границе устойчивости. Разрыву при 0

=

ω

соответствует апериодическая граница устойчивости (наличие нуле-

вого полюса в передаточной функции), а разрыву при

0≠ω – коле-

бательная граница устойчивости (наличие чисто мнимых полюсов в

передаточной функции).

5.3.1.4. Если ВЧХ непрерывна, положительна и имеет вид вогну-

той кривой (кривая 1 на рис. 5.5), то переходная характеристика мо-

нотонна.

5.3.1.5. При положительной не возрастающей ВЧХ (кривая 2 на

рис. 5.5) перерегулирование в системе не превышает 18 %, т.е.

18≤σ %.

5.3.1.6. При наличии у положительной ВЧХ максимума (величи-

на

1max

P на кривой 3 рис. 5.5) перерегулирование в системе оцени-

вается неравенством

% 100

)0(

)0(18,1

1max

⋅

−

≤σ

P

PP

. (5.10)

5.3.1.7. Если ВЧХ имеет положительный и отрицательный экс-

тремумы (величины

2max

P и

mi

n

P для кривой 4 на рис. 5.5), то

перерегулирование в системе оценивается неравенством

% 100

)0(

)0(277,018,1

min2max

⋅

−

⋅

+⋅

≤σ

P

PPP

. (5.11)

5.3.8. Острый пик на ВЧХ на угловой частоте

к

ω

соответствует

медленно затухающим колебаниям переходной характеристики с

частотой, близкой к частоте

к

ω

.

5.3.1.9. Если ВЧХ непрерывная, не возрастающая и по форме

приближается к трапецеидальной (рис. 5.6), то время переходного

процесса можно определить по соотношению

c

пп

c

4

ω

π

<<

ω

π

t .

Частота

c

ω называет-

ся

существенной час-

тотой.

Следует отметить, что

оценка перерегулирова-

ния по форме ВЧХ име-

ет весьма приблизитель-

ный характер. Реальное перерегулирование может быть в десятки раз

меньше значений, рассчитанных по формулам(5.10), (5.11).

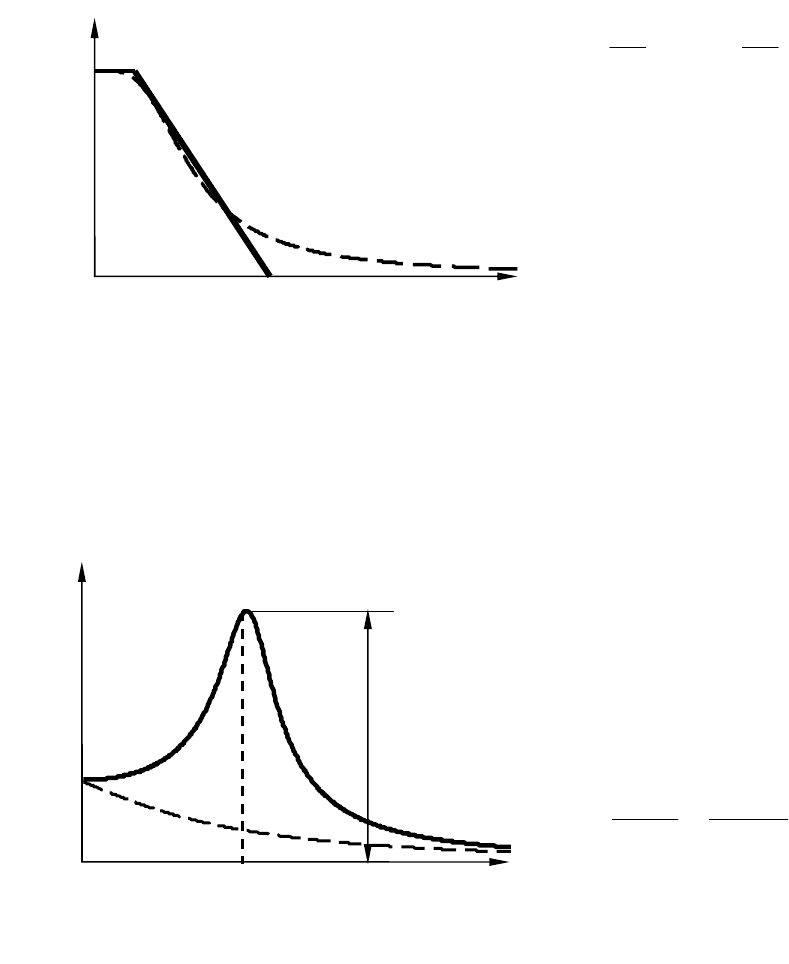
Колебательность переходной характеристики можно оценить по

величине относительного максимума амплитудной частотной харак-

теристики (АЧХ)

)(ω

A

, примерный вид которой представлен на

рис. 5.7.

Величина относи-

тельного максимума на-

зывается

показателем

колебательности

M

и

определяется соотноше-

нием

A(0)

)(

)0(

к

max

ω

==

A

M

,

где

к

ω

– частота собст-

венных колебаний пере-

ходной характеристики САУ.

При

1<

M

переходный процесс в САУ монотонный (пунктирная

линия на рис. 5.7). Чем больше

M

, тем больше колебательность. При

∞→

M

в системе имеют место незатухающие колебания.

)(ωP

)0(

P

0

с

ω

Рис. 5.6. Т

р

апе

ц

еи

д

альная ВЧХ

)(ω

A

max

A

)0(

A

0

к

ω

Рис. 5.7. Определение показателей

к

а

чества по АЧХ

Физический смысл этой оценки заключается в том, что она пока-

зывает максимально возможное отношение амплитуды выходной ве-

личины к амплитуде гармонического входного воздействия. Значе-

ние

M

примерно соответствует количеству колебаний, которые со-

вершает переходная характеристика САУ до ее входа в о бласть

5± % от установившегося значения.

Показатель колебательности

M

также связан с запасами устой-

чивости. Считается, что система имеет допустимые запасы устойчи-

вости, если

7,15,1 <<

M

, хорошие запасы устойчивости, если

3,11,1 <<

M

. Оптимальным обычно считается, если 5,12,1 <<

M

.

Вследствие предельной простоты построения ЛАЧХ удобно

пользоваться именно этой характеристикой. Информацию здесь не-

сет среднечастотная часть ЛАЧХ. На частоте среза

cp

ω

наклон

ЛАЧХ должен составлять минус 20 дБ/дек, а значение

cp

ω определя-

ется временем переходного процесса

пп

t и перерегулированием σ:

пп

cp

3

t

k

≈ω

.

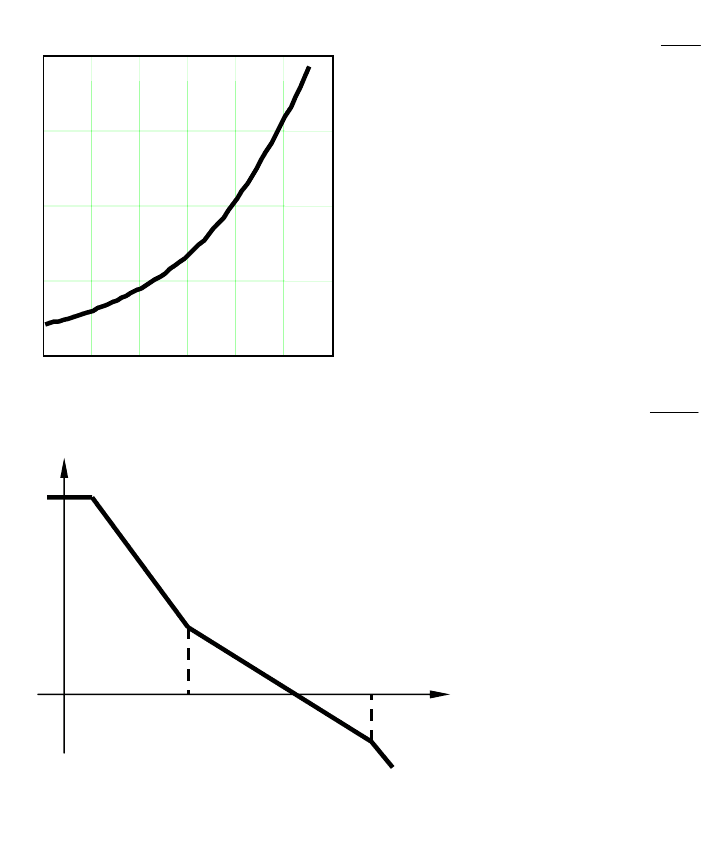
Здесь значение

k

берется по

графику, показанному на рис. 5.8 в

зависимости от величины

σ. При

этом частоты сопряжения слева и

справа от частоты среза

cp

ω , как

показано на рис. 5.9, рассчитыва-

ются по формулам

c2

2

cp

c1

ω

≈ω

,

cpc2

)42( ω÷≈ω .

Величины наклонов ЛАЧХ

слева от

c1

ω

и справа от

c2

ω

на качество переход-

ного процесса почти не

влияют.

Описанная методика оценки

времени переходного про-

цесса по ЛАЧХ применяется

при синтезе последователь-

k

σ

, %

Рис. 5.8. Зависимость

)(

σ

=

f

k

0 10 20 30 40 50 60

0

2

4

6

8

)(ω

G

c2

lg

ω

0

c1

lg ω

cp

lg ω

ω

lg

Рис. 5.9. Выбор частот сопряжения

на ЛАЧХ

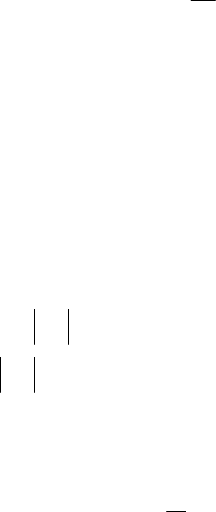
ных корректирующих устройств, изложенном в разделе 6.

5.3.2. Корневые критерии оценки качества

Данная группа критериев основана на оценке качества переход-

ного процесса по значениям полюсов и нулей передаточной функции

САУ.

Заметим, что при изучении устойчивости нас интересовали лишь

полюсы, здесь же необходимо учитывать и нули. Только в частном

случае, когда нулей нет, качество переходного процесса определяет-

ся только полюсами. Начнем рассмотрение именно такого случая.

Переходной процесс в устойчивой системе распадается на зату-

хающие и колебательные составляющие. Если найти длительность

самой длительной составляющей и величину колебательности самой

колебательной составляющей, то по ним можно оценить верхние

пределы величин длительности и колебательности всего переходного

процесса.

Время затухания отдельной составляющей определяется величи-

ной

ii

T

t

ee

−

α

=

,

где

i

α – вещественная часть i -го корня характеристического урав-

нения,

i

T – постоянная времени затухания.

Можно считать, что длительность

i -той составляющей переход-

ного процесса

ii

Tt 3

,пп

≈ , то есть длительность составляющих пере-

ходного процесса обратно пропорциональна абсолютному значению

действительной части корней характеристического уравнения.

Абсолютная величина

mi

n

i

α

называется степенью устойчиво-

сти

и обозначается

mi

n

i

α

=

η

.

При этом время переходного процесса

пп

t можно оценить нера-

венством

η

≤

3

пп

t .

Термин «степень устойчивости» связан с тем, что геометрически

η

– это расстояние от мнимой оси, являющейся границей устойчиво-

сти, до ближайшего корня (рис. 5.10).

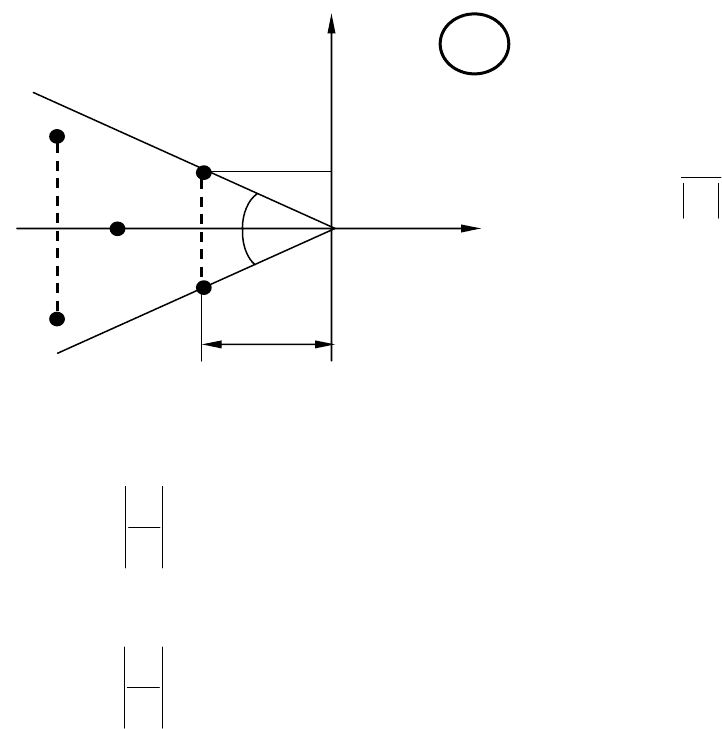
Если

i

ω

– мнимая

часть

i -го корня (рис.

5.10), то мерой колеба-

тельности считают от-

ношение

i

α

ω

: чем она

больше, тем больше ко-

лебательность состав-

ляющей переходной ха-

рактеристики.

Наиболее колеба-

тельной является со-

ставляющая, у которой

это отношение максимально. Соответствующая величина обознача-

ется

max

i

α

ω

=µ

и называется степенью колебательности. На ком-

плексной плоскости корень, определяющий наибольшую колеба-

тельность, соответствует наибольшему значению угла

max

arctg

i

α

ω

=γ

, между лучом, направленным через корень из начала

координат, и отрицательной вещественной полуосью (рис. 5.10).

Отметим также влияние на качество переходного процесса ну-

лей передаточной функции. Положительные члены полинома числи-

теля передаточной функции приведут к повышению колебательности

и убыстрению переходного процесса, а отрицательные – к затягива-

нию переходного процесса.

5.3.3. Интегральные критерии качества

С помощью интегральных критериев качества можно одним чис-

лом оценить и величины отклонений, и время затухания переходного

процесса. Для пояснения используем рис. 5.11.

Обозначим отклонение выходной величины от нового устано-

вившегося значения

)()()(

t

y

t

y

−

∞

=

∆ .

Для монотонного процесса интегральной оценкой может служить

заштрихованная площадь над кривой переходного процесса (см. рис.

5.11), то есть

p

I

m

1

p

4

p

i

ω

3

p

γ

pRe

γ

5

p

2

p

min,i

α

Рис. 5.10. К понятию степени устойчиво-

сти и колебательности

p

Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления

Подождите немного. Документ загружается.