Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления

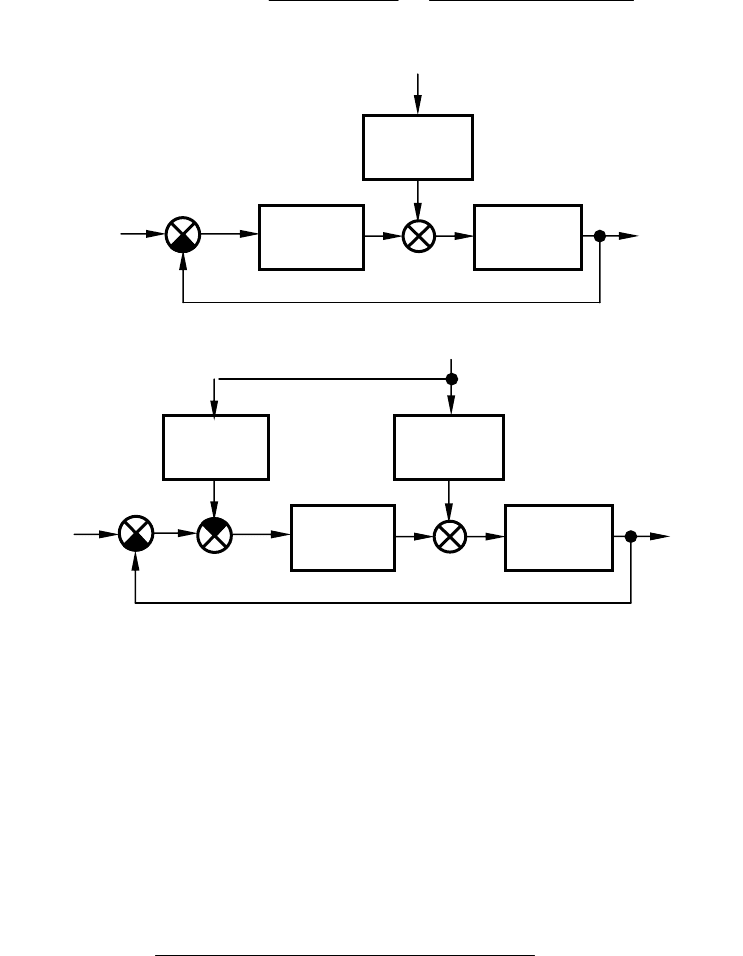
Пусть задана система, охваченная единичной отрицательной об-

ратной связью (рис. 6.3, а). Ее передаточная функция по возмущаю-

щему воздействию будет иметь вид:

)()(1

)()(

)(1

)(

21

32

рц

нсpf,

нсзf,

pWpW

pW

⋅+

⋅

=

+

=

.

Введем корректирующее устройство так, как показано на

рис. 6.3, б. Передаточная функция скорректированной САУ по воз-

мущающему воздействию в этом случае будет представлена выраже-

нием:

.

)()(1

)]()()([)(

)(

21

1к32

скзf,

pWpW

pWpWpWpW

pW

⋅+

⋅

−

⋅

=

(6.1)

Поскольку влияние возмущающего воздействия нужно уничто-

жить, необходимо принять

)(

скзf,

pW равным нулю. Это возможно

только, если в формуле (6.1) принять равным нулю выражение, рас-

положенное в квадратных скобках. Тогда условие полной инвари-

Рис.6.3. Нескорректированная (а) и скорректированная (б)

системы

f

g y

а

W

1

(p) W

2

(p)

W

3

(

(p)

f

g y

б

W

1

(p)

W

к

(p)

W

2

(p)

W

3

(

(p)

антности системы по отношению к возмущающему воздействию бу-

дет иметь вид:

)(

1

3

к

pW

pW =

. (6.2)

Выполнение условия (6.1) иногда вызывает на практике сущест-

венные трудности из-за зачастую сложной технической задачи – из-

мерения возмущающего воздействия и подачи его на вход системы,

поэтому можно ограничиться частичной инвариантностью.

Рассмотренный способ коррекции, существенно повышая точ-

ность САУ, почти не влияет на качество переходных процессов. Это

связано с тем, что знаменатель передаточной функции скорректиро-

ванной системы остается таким же, как и у нескорректированной.

Это выгодно отличает данный подход к повышению точности САУ

от других вариантов, в которых почти всегда повышение точности

сопровождалось ухудшением ее динамических характеристик.

Предметом более подробного рассмотрения будет последова-

тельная коррекция САУ.

6.2. Синтез последовательных корректирующих уст-

ройств

При введении корректирующего устройства последовательно в

контур регулирования (рис.6.1, а) его передаточная функция

)(

к

pW

умножается на передаточную функцию нескорректированной САУ

)(

н.с

pW

, т.е.

)()()(

н.скж

pWpWpW ⋅

=

,

где

)(

ж

pW – передаточная функция разомкнутой цепи скорректи-

рованной (желаемой) системы,

)(

н.с

pW – передаточная функция ра-

зомкнутой цепи нескорректированной САУ.

Поскольку логарифмические частотные характеристики последо-

вательно соединенных звеньев складываются

)()()(

н.скж

ω

GGG +=

,

то синтез последовательного корректирующего устройства наиболее

просто провести по асимптотическим ЛАЧХ. В соответствии с этим

методом, ЛАЧХ корректирующего устройства

)()()(

н.сжк

ω

GGG −

=

. (6.3)

Зная желаемую ЛАЧХ

)(

ж

ω

G

по формуле (6.3) можно построить

ЛАЧХ корректирующего устройства

)(

к

ω

G и затем, ориентируясь на

частоты сопряжения и наклоны этой ЛАЧХ синтезировать ее переда-

точную функцию на основе минимально фазовых звеньев первого

порядка.

Желаемая ЛАЧХ может быть построена на основе номограмм

Солодовникова [5]. При этом выделяются три частотных области:

низкочастотная, среднечастотная и высокочастотная.

Низкочастотная область желаемой ЛАЧХ расположена в окрест-

ности оси ординат, она определяет точностные показатели САУ и

формируется, исходя из заданной статической точности (для статиче-

ских САУ), или коэффициентов ошибок [4 -6] (для астатических

САУ). Высокочастотная область расположена выше частоты среза и

характеризует подавление системой высокочастотных помех.

Среднечастотная часть ЛАЧХ расположена в области частоты

среза и определяет основные показатели качества работы САУ в ди-

намическом режиме. Доказано, [4, 5] что если ЛАЧХ проходит

через частоту среза с наклоном минус 20 дБ/дек, то система в

замкнутом состоянии будет иметь наименьшую колебательность и

наилучшие показатели качества.

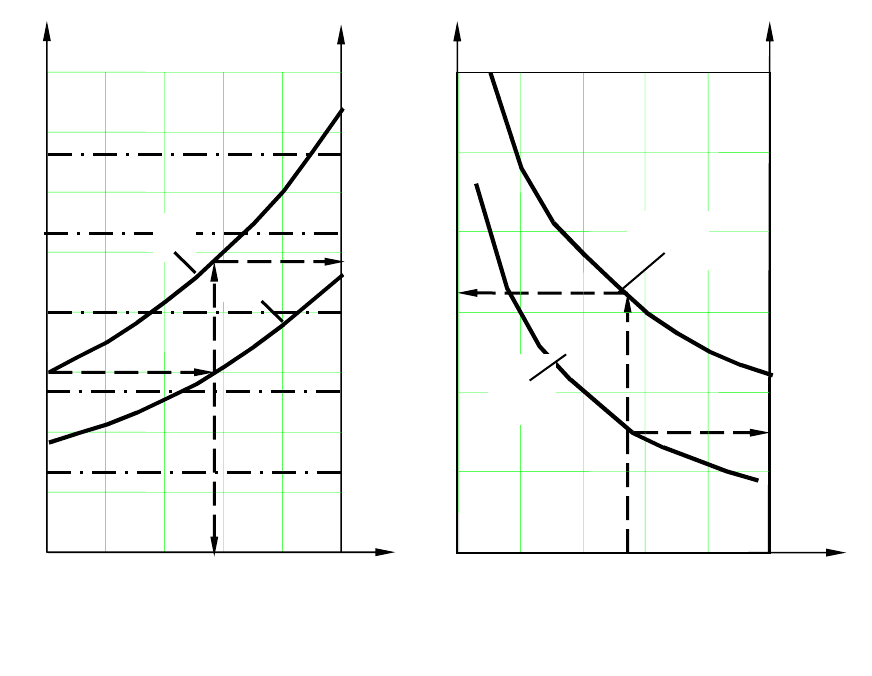
Одним из подходов к построению желаемой ЛАЧХ является ре-

шение этой задачи с помощью номограмм Солодовникова, приведен-

ных на рис. 6.4. Они представляют собой зависимости перерегулиро-

вания

σ

, запаса устойчивости по фазе

ϕ

∆

, параметров

λ

и

g

L от

максимума вещественной частотной характеристики

max

P

.

При известных значениях перерегулирования

σ

и времени пере-

ходного процесса

пп

t величина

σ

отмечается на графике

()

max1

Pf=σ

и по нему определяются значения

max

P

, а затем из гра-

фика

()

max2

Pf=

λ

находится величина параметра

λ

. Этот путь для

30=σ % показан пунктирной линией со стрелками на рис. 6.4, а, со-

гласно таким построениям получаются значения

6,3 ,28,1

max

≈

λ

≈P . Тогда частота среза, через которую желаемая

ЛАЧХ должна пройти с наклоном –20 дБ/дек, определится из соот-

ношения

пп

cp

ω

t

π

λ

⋅

≈

. (6.4)

Далее для полученной величины

max

P по кривым

()

max3

PfL

g

=

и

()

max4

Pf=ϕ∆ , приведенным на рис. 6.4, б, определяются значения

параметра

g

L и запаса устойчивости

ϕ

∆

, если информация о нем

необходима. Этот путь для

30

=

σ

% также отражен пунктирной ли-

нией со стрелками и, согласно нему, получаются значения

5,12≈

g

L

дБ,

42≈

ϕ

∆ градуса.

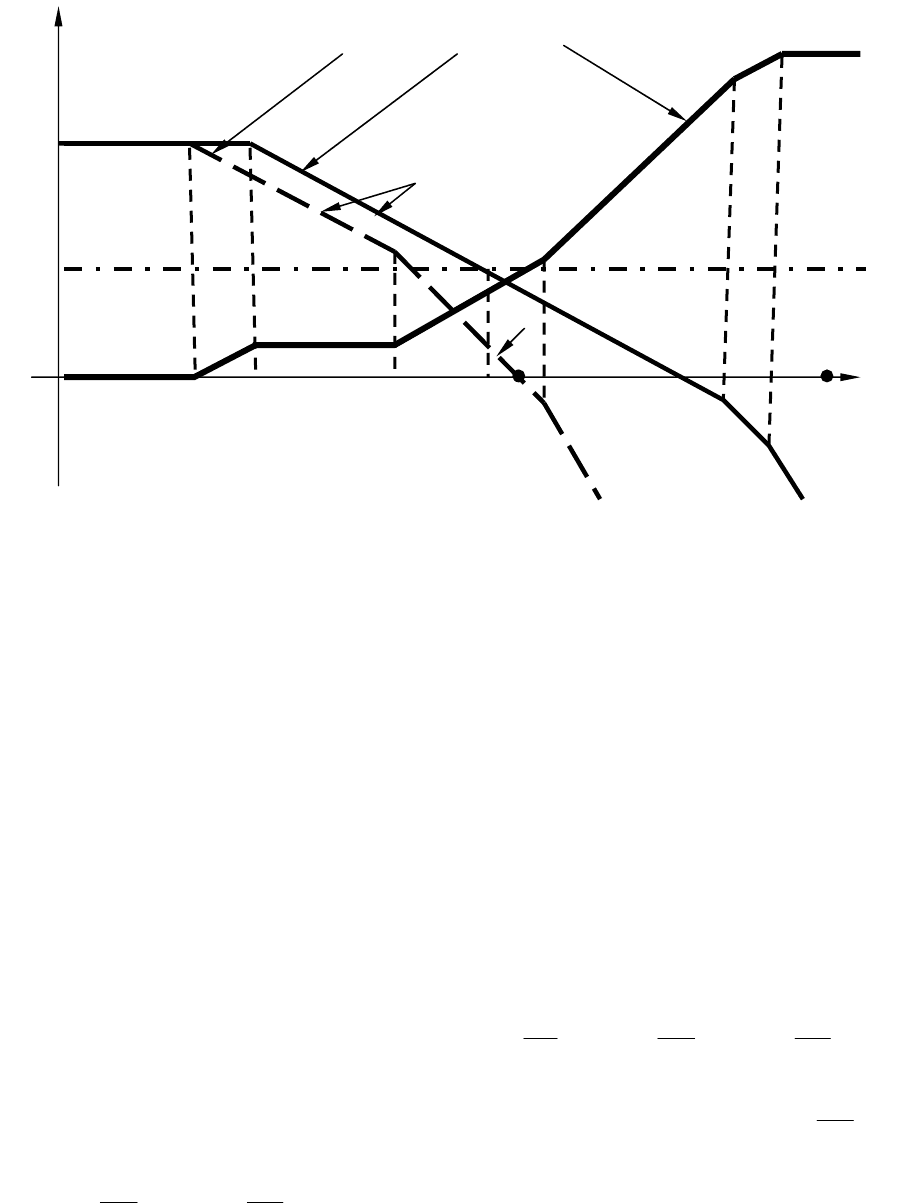
Далее можно приступить к построению желаемой ЛАЧХ и ЛАЧХ

корректирующего устройства. Строится ЛАЧХ нескорректированной

САУ

)(

н.с

ω

G , на ось

ω

lg в логарифмическом масштабе наносится

рассчитанная по формуле (6.4) частота среза

cp

ω и прямая, пересе-

кающая ось ординат на уровне

g

L (рис. 6.5). Через частоту среза

проводится прямая, проходящая с наклоном -20 дБ/дек. В точке пе-

ресечения этой прямой и уровня

g

L определяется частота

0

ω и отре-

зок длиной

(

)

cp0

, ω

ω

откладывается симметрично относительно час-

тоты среза справа от нее до точки

01

ω

. На интервале

01cp

ω

<ω<ω

произвольно выбираются две частоты

4

ω

и

5

ω

, на которых желаемая

ЛАЧХ принимает наклоны –40 дБ/дек и –60 дБ/дек соответственно.

ϕ

∆

, град L

g

, дБ

35

30

25

20

15

10

max

P

б

1 1.1 1.2 1.3 1.4 1.5

10

20

30

40

50

60

70

ϕ

∆

L

g

,

Рис.6.4. Номограммы Солодовникова

σ, % λ

5

4

3

2

1

max

P

а

1 1.1 1.2 1.3 1.4 1.5

0

10

20

30

40

50

60

70

80

λ

σ

Если статическая ошибка нескорректированной САУ удовле-

творяет заданной точности, то низкочастотный участок желаемой

ЛАЧХ стыкуют с ЛАЧХ нескорректированной САУ так, как это бу-

дет наиболее удобно с позиции графических построений. В частно-

сти, на рис. 6.5 эта стыковка произведена на уровне

0

G на частоте

6

ω , но может быть произведена в любом другом месте при

0

ω<ω .

ЛАЧХ корректирующего устройства

)(

ω

к

G

получается путем

графического вычитания ЛАЧХ нескорректированной системы

)(

н.с

ωG из желаемой ЛАЧХ )(

ω

ж

G . По наклонам )(ω

к

G легко ви-

деть, что корректирующее устройство состоит из трех форсирующих

звеньев с постоянными времени

1

к1

1

ω

=τ

,

2

к2

1

ω

=τ

,

3

к3

1

ω

=τ

и

трех инерционных звеньев с постоянными времени

6

к1

1

ω

=T

,

4

к2

1

ω

=T

и

5

к3

1

ω

=T

, т.е. представляет собой трехзвенный фильтр с

передаточной функцией

)(ω

G

)(

н.с

ω

G

)(

ω

ж

G

)(

ω

к

G

0

+20

0

G

-20 +40

g

L

0 +20 -40

+20

4

ω

5

ω

lg

0

1

ω

6

ω

2

ω

0

ω

3

ω

cp

ω

-40

01

ω

-60 -60

Рис. 6.5. Построение желаемой ЛАЧХ и ЛАЧХ корректирующего

устройства

)1)(1)(1(

)1()1()1(

)(

к3к2к1

к

+++

+

τ

+

τ

+

τ

=

pTpTpT

ppp

pW

.

Поскольку нескорректированная САУ состоит из трех инерцион-

ных звеньев с постоянными времени

1

ω

=T

,

2

1

ω

=T

,

3

к3

1

ω

=τ

с

общим коэффициентом передачи

20

p

0

10

G

K = (это видно по ее ЛАЧХ),

то

1к1

T=τ ,

2к2

T=τ ,

3к3

T

=

τ и при введении корректирующего зве-

на последовательно в нескорректированную САУ происходит сокра-

щение или, как говорят, компенсация инерционных звеньев нескор-

ректированной системы:

,

)1)(1)(1(

)1)(1)(1()1)(1)(1(

)1()1()1(

)()()(

к3к2к1

p

321

p

к3к2к1

н.скж

+++

=

+++

⋅

+++

+τ+τ+τ

=

⋅

=

pTpTpT

K

pTpTpT

K

pTpTpT

ppp

pWpWpW

(6.5)

а поскольку

2к32к21к1

, , TTTTTT

<

, то в скорректированной

системе следует ожидать существенного улучшения показателей ка-

чества.

Далее по выражению (6.5) находится передаточная функция

замкнутой скорректированной САУ, рассчитываются показатели ка-

чества и, если перерегулирование превышает заданное значение,

увеличиваются частоты

4

ω

,

5

ω

и пересчет переходной характери-

стики проводится заново до получения перерегулирования, близкого

к заданному. Если это условие выполнено, то, как правило, время пе-

реходного процесса меньше заданного, т.е. требование к быстродей-

ствию САУ выполняется автоматически.

Рассмотренная методика синтеза последовательных корректи-

рующих устройств дает хорошие результаты только при безынерци-

онных и мало инерционных обратных связях. Если обратная связь

системы имеет повышенную инерционность, т.е. ее постоянная вре-

мени

cp

oc

1

ω

≥T

, то переходный процесс, за счет форсирующего дей-

ствия такой связи, сопровождается повышенным перерегулировани-

ем и настройка САУ на заданное значение

σ

крайне затруднительна.

В этом случае систему настраивают только на заданное время пере-

ходного процесса.

Применение описанного варианта синтеза последовательного

корректирующего устройства особенно эффективно в расчетах с ис-

пользованием персонального компьютера, например, при работе в

системе MathCAD.

6.3. Оптимальные характеристики САУ. Настройка

систем на технический и симметричный оптимумы

В ряде областей техники, например, в многоконтурных системах

электропривода с подчиненным регулированием, синтез последова-

тельных корректирующих устройств осуществляется по-другому.

Подчиненное регулирование предполагает независимость работы

контуров системы. Так, например, в двухконтурной системе при ра-

боте внутреннего контура внешний отключен и, наоборот, если рабо-

тает внешний контур, то отключается внутренний. Это возможно

лишь в том случае, если каждый из контуров будет настроен на тех-

нический или симметричный оптимум.

Считается [9, 10], что система будет иметь наилучшие (опти-

мальные) переходные процессы, если передаточная функция ее ра-

зомкнутой цепи будет иметь вид:

,

)1(2

1

)(

ТОрц,

+

=

µµ

pTpT

pW

(6.6.)

где

µ

T - эквивалентная некомпенсируемая постоянная времени САУ.

Если для САУ имеет место (6.6), то говорят, что она настроена на

технический оптимум (ТО).

Известно [9,10], что перерегулирование в САУ, для которой име-

ет место равенство (6.6), не превышает 5 %. Тогда, согласно номо-

граммам Солодовникова, время переходного процесса можно оце-

нить по соотношению:

ср

ТОпп,

2

ω

≈t

.

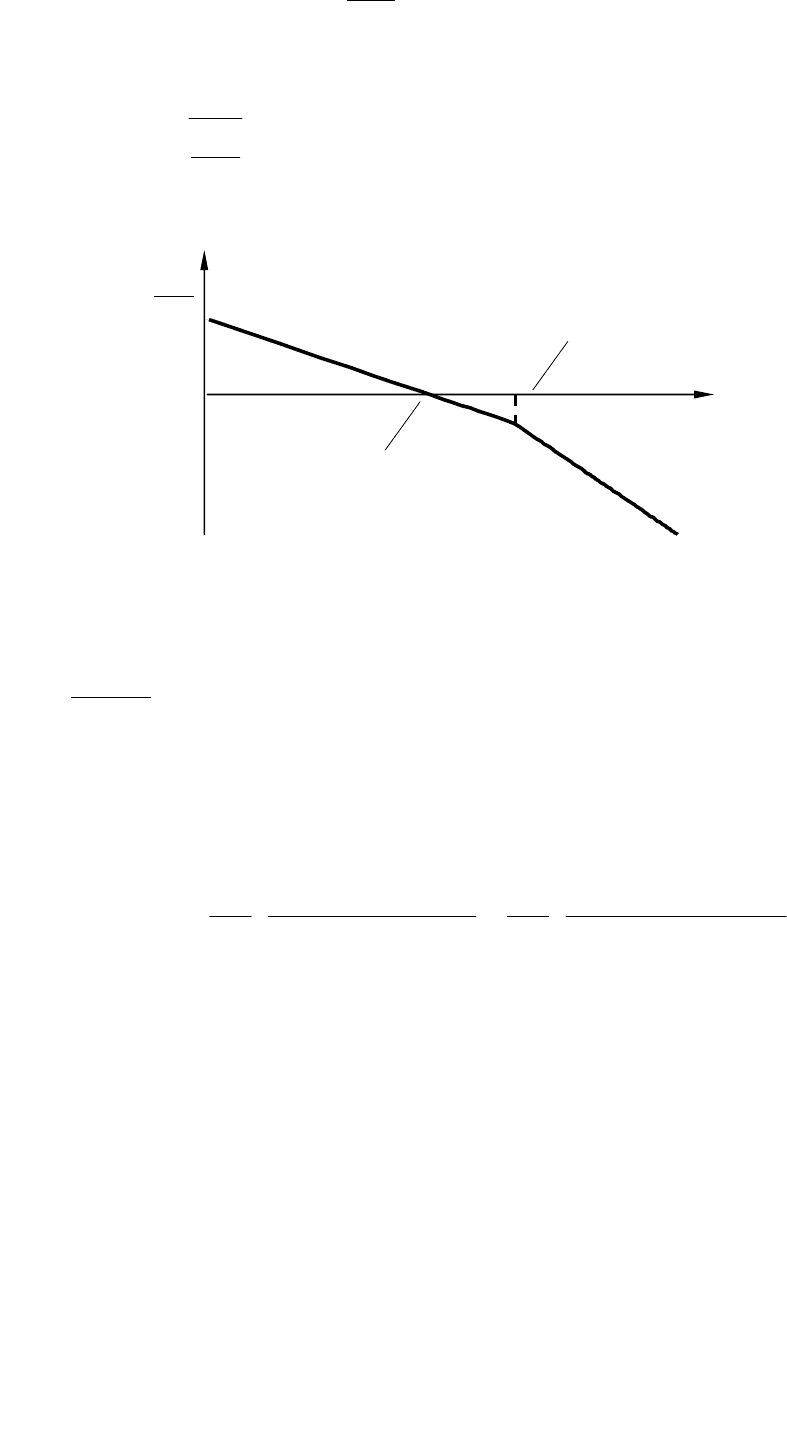
На рис. 6.6. приведена ЛАЧХ для системы, настроенной на ТО.

Так как частота среза

µ

=ω

T

cp

2

1

, то

µ

=≈ T

T

t 4

2

1

2

ТОпп,

. (6.7)

Из выражения (6.7) следует, что для САУ, настроенной на ТО

4

TOпп,

t

T

=

µ

.

Если систему, настроенную на ТО, замкнуть инерционной обрат-

ной связью с коэффициентом передачи

oc

k и постоянной времени

oc

T , то ее передаточная функция будет иметь вид:

122

11

1)1(2

11

)(

2

oc

ТОзg,

++

+

⋅=

++

+

⋅=

µµ

pTpT

pT

kpTpT

pT

k

pW

.

На рис. 6.8 изображены переходные характеристики САУ, на-

строенной на ТО, при единичном входном воздействии,

1

=

oc

k ,

05,0=

µ

T с и различных значениях

oc

T . При

µ

TT

=

oc

(кривая 1) пе-

ререгулирование составляет около 6,7%, при

µ

TT 5,0

=

oc

(кривая 2)

– около 4,9%, при

0=

oc

T (кривая 3) – около 4,3%. При этом время

переходного процесса

3,0

1

≈

пп

t с при

µ

TT

=

oc

, 18,0

2

≈

пп

t с при

µ

TT 5,0=

oc

, 2,0

3

≈

пп

t с при 0

=

oc

T . Для сравнения здесь также

G(ω)

µ

T2

1

lg20

-20 дБ/дек

µ

=ω

T

1

c

µ

=ω

T2

1

cp

lg ω

-40 дБ/дек

Рис.6.6. ЛАЧХ системы, настроенной на ТО

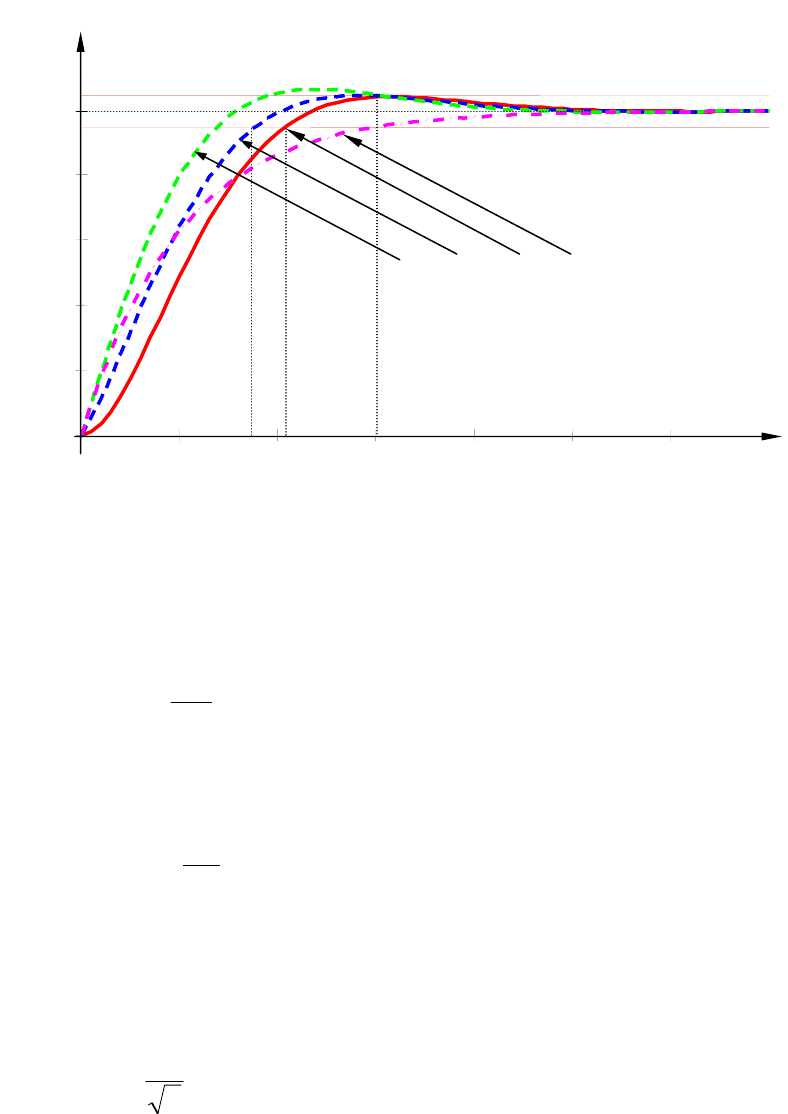
приведена кривая 4, соответствующая апериодическому переходному

процессу с постоянной времени

µ

T (кривая 4), для нее

3,0

1

≈≈

пппп4

tt

с.

Из анализа приведенных переходных характеристик можно сде-

лать следующие выводы.

6.3.1. Если

2

oc

<

µ

T

, то перерегулирование превышает 5% и время

переходного процесса увеличивается примерно в 1,5 раза по сравне-

нию с расчетным

2,04

пп

=

µ

Tt с.

6.3.2. Если

2

oc

>

µ

T

, то перерегулирование не превышает 5% и

время переходного процесса уменьшается по сравнению с расчет-

ным.

6.3.3. Если

0=

oc

T

, то САУ идеально настроена на ТО,

она эквивалентна колебательному звену с коэффициентом демпфи-

рования

707,0

2

1

≈

=ξ , время переходного процесса совпадает с

расчетным.

y(t)

1 2 3 4

t

пп

2

t

пп3

t

пп4пп1

tt

=

с

Рис. 6.8. Переходные характеристики САУ, настроенной на

ТО, при различной инерционности ее цепи обратной св

я

зи

0 0.4 0.5 0.6

0.2

0.4

0.6

0.8

1

6.4.4. Поскольку отношение

5,1≈

пп2

пп4

t

иногда САУ, настроен-

ную на ТО, приближенно эквивалентируют инерционным звеном, то

есть

12

11

1)1(2

11

)(

ococ

ТОзg,

+

⋅≈

++

⋅=

µµµ

pTkpTpTk

pW

. (6.8)

Этим приемом используется при настройке на ТО многоконтур-

ных систем, в частности, электромеханических систем (ЭМС).

Одна из задач настройки системы на ТО – сделать контур регу-

лирования астатическим. Этого достичь не удается, если в состав

объекта регулирования входит интегрирующее звено. Тогда стремят-

ся получить передаточную функцию системы, ЛАЧХ которой на час-

тоте среза сохраняет свойственный для ТО наклон –20 дБ/дек и ме-

няет этот наклон до -40 дБ/дек в области низкой

н

ω

и высокой

в

ω

частот пропускания, отличающихся от частоты среза

ср

ω не менее,

чем в два раза.

Одним из вариантов таких САУ являются системы, настроенные

на

симметричный оптимум (СО) [9, 10]. При этом переда-

точная функция разомкнутой цепи для САУ, обеспечивающих харак-

теристики СО, имеет вид:

)(

4

14

)1(2

1

4

14

)(

ТОрц,CОрц,

pW

pT

pTpTpT

pT

pW ⋅

+

=

+

⋅

+

=

µ

µµµ

µ

. (6.9)

Известно [9, 10], что для системы, настроенной на СО, перерегу-

лирование составляет около 43 - 45 %. Тогда, согласно номограммам

Солодовникова, время переходного процесса можно оценить по со-

отношению:

ср

СОпп,

4

ω

≈

t . (6.10)

На рис. 6.9 приведена ЛАЧХ для САУ, передаточная функция ра-

зомкнутой цепи которой представлена выражением (6.9). Для нее

µ

=ω

T

1

н

,

µ

=ω

T2

1

cp

и

µ

=ω

T4

1

в

, поэтому, в соответствии с (6.10)

Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления

Подождите немного. Документ загружается.