Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.


Передаточные функции САУ при 0
=
q (установившиеся состав-
ляющие):
≤ε<γ
−−−
−
γ≤ε≤
−−−
−−−
=
=ε=ε
βγβ−
βε−βχ
βγβ−
βε−βχβ−βε−
.1
)]1(1[1
)1(
,0
)]1(1[1
)1()1(
),0(] ,[
при
при
и
и
и
и
*
зуст
eke
ee
k
eke
eeee
k
Wny
Числители передаточных функций САУ при
1
~
qq
=
:
[
]
≤ε<γ−
γ≤ε≤−−−
=ε
βε−βχ
βε−βχβ−βε−
.1 )1(
,0 )1()1(
),
~
(
при
при
1
1
~
и
~
и
*
з
eeek
eeeeek
qB
q
q
В соответствии с (11.2) при количестве полюсов
1=m расчетные
выражения для переходных характеристик САУ будут иметь вид:
≤ε<γ
−
−
−
−
−−−
−
γ≤ε≤
−
−−−
−
−
−−−
−−−
=ε
βε−βχ
βγβ−
βε−βχ
βε−βχβ−βε−
βγβ−
βε−βχβ−βε−
.1
1
)1(
)]1(1[1
)1(
,0
1
)1()1(
)]1(1[1
)1()1(
] ,[
при
при
1
1
1
1
1
1
~
~
~
и
и
и
~
~
~
и
и
и
nq
q
q
nq
q
q
e
e
eee
k
eke
ee
k
e
e
eeeee
k
eke
eeee
k
ny
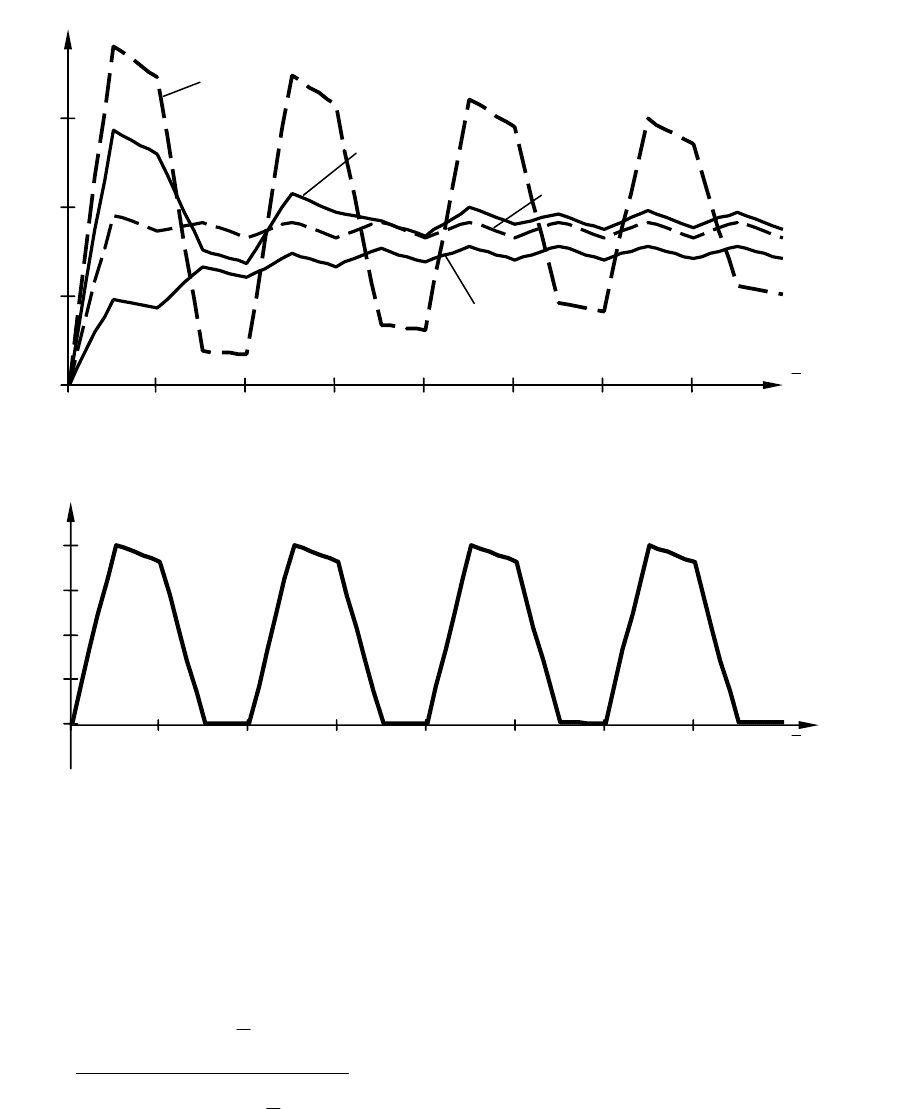
На рис. 11.1,
а приведены переходные характеристики системы,
рассчитанные по приведенным выше соотношениям при
гри,и
kk < , а
на рис. 11.1, б – переходная характеристика САУ при
гри,и
kk = .
Внутри интервалов
γ
+
≤
ε
+
≤ nnn и 1+
<
ε
+
<
γ
+
nnn выходная
величина
] ,[ εn
y
изменяется по экспоненциальной зависимости. При
гри,и
kk <
переходная составляющая затухает, причем при малых
значениях
и
k это затухание имеет апериодический характер и с рос-
том
и
k процесс затухания ] ,[
п
ε
ny становится колебательным.
В установившемся режиме выходная величина пульсирует с пе-
риодом квантования
T
от максимального
=
max
y
−−−
−
=
β
β−
β
−
111
1
2
и
2
и
eke
e
k
до минимального
] ,[ εn
y
20
и
=k
15
и
=
k
10
и
=
k
5
и
=
k
ε
+
=
n
t
a
0 12 34567
0.5
1
1.5
] ,[ εn
y
гри,и
kk
=
ε
+
=
n
t
б
0 12 34567
0.5
1
1.5
2
Рис. 11.1. Переходные характеристики САУ с АИМ для
5,0=
γ
при
гри,и
kk
<
(а) и при
гри,и
kk
=
(б)

−−−
−
=
β
β−
β
β−
111
1
2
и
2
иmin
eke
ee
ky
значений. В этом случае часто гово-
рят не об установившемся, а о
квазиустановившемся режиме ра-
боты системы и оценивают среднее значение выходной величины
как
2
minmax
ср
yy
y
−
=
. При
гри,и
kk
=
(рис. 11.1, б) на выходе САУ
будут иметь место устойчивые автоколебания с периодом
T
2 .
Для
1=
γ
из первого выражения формулы (11.4) получим
)]1(1[
)1(
),(
и
и
1
*
з
|
−−−
+−−
=ε
ββ−
β
ε
−
β
−
β
ε
−
=γ
ekee
eeee
kqW
q
q
,
тогда
и
и
1
*
з
1
уст
1
),0(] ,[
||
k
k
Wny
+
=ε=ε
=γ=γ
,
)]1()1[(),(
1
~
и
1
*
з
|
βε−ββ−βε−
=γ
−−−=ε eeeeekqB
q
,
.
1
)1(
1
1
] ,[
1
1
1
~
~
~
и
и
1
|
−
+−−
−
+
=ε
βε−β−βε−
=γ
nq
q
q
e
e
eeee
k
kny
(11.5)
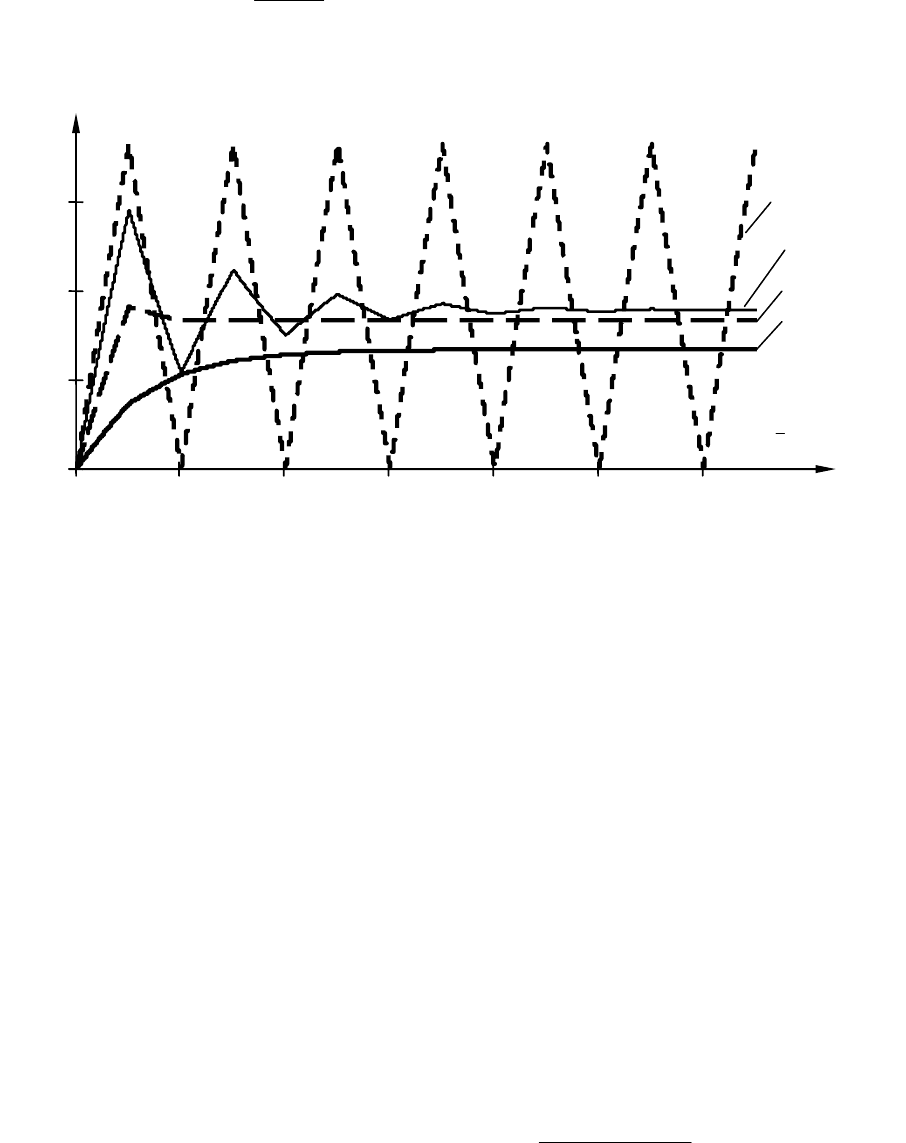
На рис. 11.2 показаны переходные характеристики САУ, рассчи-
танные по формуле (11.5) при различных значениях
и
k . При малых
значениях
и
k , например, при 2
и
=
k переходный процесс имеет апе-
риодический характер, причем такой же, как и у непрерывных сис-
тем. При больших значениях
и
k переходный процесс становится ко-
лебательным, причем на интервалах
1
+
<
<
n
t
n
переходная состав-
ляющая
|
1
п
] ,[
=γ
εny изменяется по экспоненциальному закону. При
гри,и
kk = на выходе САУ будут иметь место устойчивые автоколе-
бания с периодом
T
2 . Для устойчивой системы установившееся зна-
чение
и
и
1
уст
1
] ,[
|
k
k
ny
+
=ε
=γ
определяется значением коэффициента
передачи
и
k и не зависит от величин n и
ε
.
Существуют и другие способы расчета переходных характери-
стик САУ с АИМ. В частности, они могут быть рассчитаны через
импульсные переходные характеристики или по вещественной час-
тотной характеристике [11].
11.2. Показатели качества управления в системах с
АИМ
11.2.1 Показатели качества в статическом режиме работы
При произвольном внешнем воздействии
],[
ε
n
f
установившаяся
составляющая
] ,[
уст
εny может быть рассчитана по формуле [11]:
∑
∞
=
−∆
ε−+ε=ε
1
0уст
!
]0,[
)()1(]0 ,[)(] ,[
k
k
k
k
k
knf
dnfdny
, (11.6)
] ,[ εny
гри,и
kk
=
8
и
=
k
5
и
=
k
2
и
=
k
ε
+
=
n
t
Рис.11.2. Переходные характеристики САУ с АИМ при
1
=
γ
0 2 4 6 8 10 12
0.5
1
1.5

где
∑
∞
=
ε=ε
0
)(
з
] ,[)(
m
k
k
mmwd – моменты импульсной характеристи-
ки замкнутой импульсной системы
] ,[
з
ε
тw , ]0,[ knf
k
−∆ –
k
-тая
разность для решетчатой функции
]0,[
k
n
f
−
.
Установившаяся ошибка в замкнутой системе (см. рис. 9.7)
] ,[] ,[] ,[
устуст
ε
−ε
=
ε nynfnx . (11.7)
В соответствии с интерполяционной формулой Ньютона, пред-
ставим ] ,[
ε
n
f
в виде
∑
∞
=
−
−∆
ε
=ε
1
)(
]0,[
!
] ,[
k
k
k
knf
k
nf , (11.8)
где
1 ),1()2)(1(
)0()(
=ε−+ε⋅⋅⋅+ε+εε=ε
−
k
k
– так называемая нис-
ходящая факториальная функция.
Подставив (11.6) и (11.8) в (11.7), получим формулу для расчета
установившейся ошибки:
[]
∑
∞
=
−
−∆
⋅ε−−ε=ε
1
)(
уст
!
]0 ,[
)()1(] ,[
k
k
k
kk
k
knf
dnx
. (11.9)
Из формулы (11.9) следует, что установившаяся ошибка пропор-
циональна
k
-той разности внешнего воздействия ]0 ,[ knf
k
−∆ . Ко-
эффициенты пропорциональности
[]
)()1(
!
1
)(
)(
ε−−ε⋅=ε
−
k
kk
k
d
k
C (11.10)
называются коэффициентами ошибок.
Рассмотрим некоторые частные случаи применения формулы
(11.9). Пусть к следящей САУ с АИМ приложено воздействие вида
r
ttf )( = . Соответствующая решетчатая функция будет равна
r
nnf )(] ,[ ε+=ε .

Полагая ... ,2 ,1 ,0
=
r
получим
воздействия вида постоянной (
0=
r
),
линейной (
1
=
r
) и квадратичной
(
2
=
r
) функций (рис. 11.3). Значения
]0,[n
f
и их разностей ]0,[ knf
k
−∆
при
... ,2 ,1 ,0
=
r
будут равны соот-
ветственно:
0
=
r
: 1]0 ,[ =n
f
,
,0]0,[ =−∆ knf
k
... ,3 ,2 ,1=
k
;
1=
r
: nn
f
=
]0,[ ,
,1]0,1[
=
−
∆ n
f
,0]0,[ =−∆ knf
k
... ,3 ,2 ,1
=
k
;
2=
r
:
2
]0 ,[ nnf = ,
,12]0,1[
−
=
−
∆ nn
f
,2]0,1[
2
=−∆ nf
,0]0,[ =−∆ knf
k
... ,3 ,2 ,1
=
k
.
Подставляя в формулу (11.9) полученные значения, будем иметь:
для
0=
r
)(1] ,[
0уст
ε
−
=
ε
dnx ;
для
1=
r
[
]
)()(1] ,[
10уст
ε
+
ε
+
ε
−
=
ε
dndnx ;
для
2=
r
[]
[
]
)()1()12()()(1] ,[
21
2
0уст
ε−+εε+−ε+ε+ε−=ε dndndnx .
Отсюда следует, что при
1)(
0
=
ε
d
будет отсутствовать статиче-
ская ошибка; при
1)(
0
=
εd ,
ε
−
=
ε
)(
1
d будет отсутствовать устано-
вившаяся ошибка при постоянной скорости (скоростная ошибка); при
1)(
0
=εd
,
ε−=ε)(
1
d
,
)1()(
2
+
ε
ε
=
ε
d
будет отсутствовать устано-
вившаяся ошибка при постоянном ускорении (ошибка по ускорению)
входной величины.
Замкнутая система с АИМ, у которой отсутствует установившая-
ся ошибка при воздействии вида
r
ttf )( = , обладает астатизмом
)(
t
f
2=
r
1=
r
0=
r
ε
+= n
t
Рис. 11.3. Воздействия
вида
r
ttf )( =

r
-ого порядка. Условие получения астатизма
r
-ого порядка сводит-
ся к обращению в нуль коэффициентов ошибок, т.е. к равенствам
)(
)1()(
kk
k
d
−
ε−=ε
(
)
rk ... ,2 ,1 ,0
=
, (11.11)
которые при
0=
ε
принимают вид
1)0(
0
=d , 0)(
=
ε
k
d ,
r
k
... ,2 ,1 ,0
=
.
Условия астатизма (11.11) систем с АИМ можно сформулировать
по-другому. Моменты импульсной характеристики можно также оп-
ределить по передаточной функции замкнутой системы [11]:
|
0
*
з
),(
)(
!
1
)(
=
ε=ε
q
kq
k
k
qW
ed
d
k
d . (11.12)
В соответствии с формулой (11.12),
астатизм
r
-ого порядка
достигается, если передаточная функция замкнутой САУ с АИМ
при
0=q обращается в единицу, а производные передаточной
функции по
q
e до
r
-ого порядка обращаются в
)(
)1(
kk −
ε− .
Определим условия реализации астатической САУ. Уравнение
замкнутой САУ с АИМ относительно изображения входной величи-
ны импульсного элемента (сигнала ошибки или рассогласования)
имеет вид (см. формулу (9.19)):
)(
)0,(1
1
)(
*
*
p
*
qF
qW
qX
+
= .
Для того, чтобы система с АИМ имела астатизм порядка
r
по от-
ношению к входному воздействию
][n
f
, передаточная функция
)0,(
*
p
qW должна иметь нулевой полюс кратности
r
, т.е. иметь вид
)()1(
),(
)0,(
*
пp,
*
p
*
p
qAe
qB
qW
rq
−
ε
=
, где полином
0
)1(
1
)(*
пp,
)( aeaeaeaqA
q
r
qrm
rm
qrm
rm
++⋅⋅⋅++=
−
−
−−
−
−
содержит
только простые нули, отличные от нуля. Тогда ошибка

)0,(
),()0,()1(
)0,()1(
)0,(
)0,()1(
),(
1
1
)0,(
*
*
p
*
пp,
*
пp,
*
*
пp,
*
p
*
qF
qBqAe
qAe
qF
qAe
qB
qX
rq
rq
rq
ε+−
−
=
=
−
ε
+
=
становится равной нулю при
0
=
q .
Следовательно,
для того чтобы САУ с АИМ имела астатизм
r
-ого порядка, необходимо и достаточно, чтобы передаточная
функция ее непрерывной части
)(
н
qW
содержала
r
нулевых по-
люсов.
Это означает, что непрерывная часть системы должна со-
держать
r
интегрирующих звеньев.
Пример 11.2. Рассчитать коэффициенты ошибок для САУ с
АИМ, изображенной на рис. 9.8, при
2,0
=
β
,
1
=
γ
,
0=
ε
, 5
и
=k .
При
0=ε нисходящая факториальная функция 0
)(
=
ε
−k
для лю-
бого
k
. Оценим первые три коэффициента ошибок, т.е. при
2 ,1 ,0=
k
в соответствии с (11.10) будем иметь
)0()0(
00
dC = , )0()0(
11
dC
−
=
,
2
)0(
)0(
2
2
d
C =
.
При
1=
γ
, 0=ε передаточная функция системы будет иметь вид
)]1(1[
1
)0,(
и
и
*
з
−−−
−
=
ββ−
β
−
ekee
e
kqW
q
.
В соответствии с формулой (11.12)
833,0
51
5
1
)0,()0(
и
и
0
*
з0
|
=
+
=
+
==
=
k
k
qWd
q
,
следовательно,
833,0)0()0(
00
=
=
dC
.
При
1=
k

,766,0
)]1(1[1
1
)]1(1[
1
)0,(
)(
)0(
2
и
и
0
2
и
и
0
*
з1
||
−=
−−−
−
=
=
−−−
−
=
=
ββ−
β−
=
ββ−
β−
=
eke
e
k
ekee
e
kqW
ed
d
d
q
q
q
q
тогда
766,0)()0(
11
=ε−= dC .
При 2=
k
,704,0
)]1(1[1
1
)]1(1[
1
)0,(
)(
2
1
)0(
3
и
и
0
3
и
и
0
*
з
2
2
2
||
=
−−−
−
=
=
−−−
−
=
⋅=
ββ−
β−
=
ββ−
β−
=
eke
e
k
ekee
e
kqW
ed
d
d
q
q
q
q
следовательно,
352,0
2
)0(
)0(
2
2
==
d
C
.
Таким образом, анализируемая система является статической,
причем ее статическая ошибка при подаче на вход единичного воз-
действия
167,0833,01)0(1
0
=
−
=−=∆ C весьма велика. Скоростная
ошибка и ошибка по ускорению (оцениваются при подаче на вход
линейно и квадратично изменяющихся воздействий) также большие.
11.2.2.
Оценка качества управления в динамических ре-
жимах
Требования к качеству переходного процесса в системах с АИМ
аналогичны к требованиям для непрерывных САУ и выражаются в
допустимых значениях перерегулирования
σ
и времени переходного
процесса
пп
t , которое может быть выражено в относительных еди-
ницах
T
t
n
пп
пп
= , где
T
– период квантования (чередования импуль-
сов). Величины
σ и
пп
n могут быть получены непосредственно из
переходной характеристики САУ, как это делается в непрерывных
системах.
Остановимся на косвенных некоторых оценках качества пере-
ходного процесса.
Наиболее простой оценкой является степень устойчивости
и
η
,
под которой понимают минимальную по абсолютной величине веще-
ственную часть полюсов передаточной функции
)(
),(
),(
*
з
*
з
*
з
qA
qB
qW
ε
=ε .
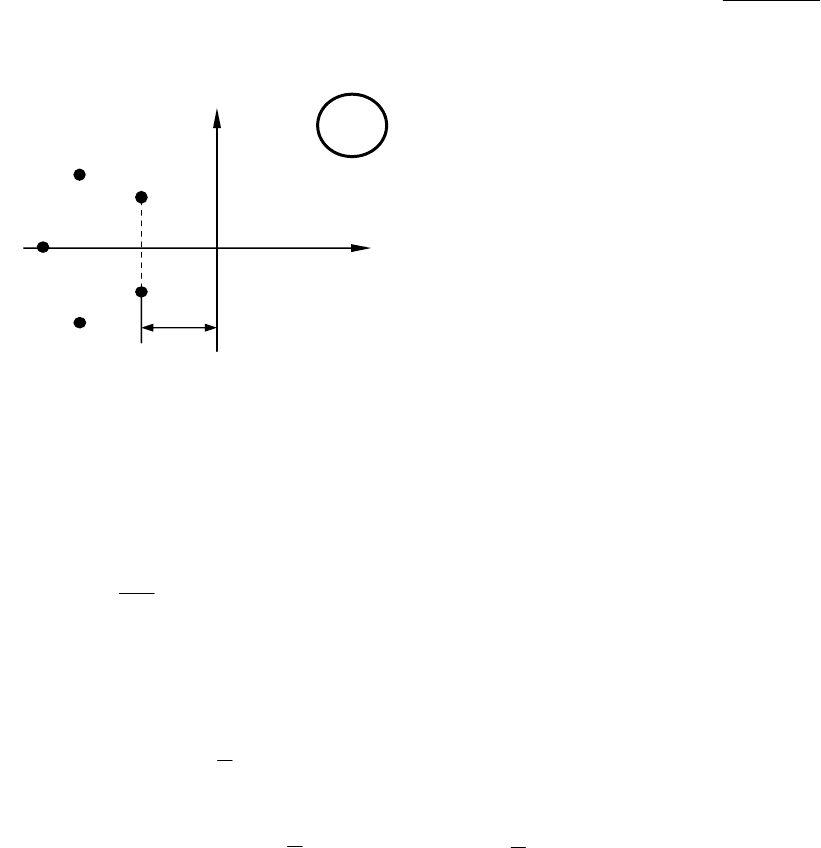
Геометрически степень ус-
тойчивости
и
η
определяется
расстоянием от мнимой оси до
прямой, проходящей через
ближайшие к ней нули, как по-
казано рис. 11.4, и определяется
наиболее медленно затухающей
компонентой переходного про-
цесса. Чем больше
и
η
, тем бы-
стрее затухает переходный
процесс. Длительность (время)
переходного процесса можно
приблизительно оценить
неравенством
и
пп
3
η
≤n
. (11.13)
Иногда системы с АИМ проектируют на заданную степень ус-
тойчивости. Для этого в характеристическом полиноме
)(
*
з
qA произ-
водят замену
и
η−= qq
, где
0
и
>
η
– заданное значение. Эта замена
соответствует переносу мнимой оси на величину
и
η
. Система, кото-
рой соответствует
),(
и
*
з
εη−qW
или
)(
и
*
з
η−qA
, называется преоб-
разованной. Если преобразованная САУ с АИМ устойчива, то сте-
пень устойчивости исходной системы больше
и
η
, если она неустой-
чива, то степень устойчивости исходной системы меньше
и
η
. Нако-
нец, если преобразованная система находится на границе устойчиво-
сти, то степень устойчивости исходной системы точно равна
и
η
.
Граница, соответствующая преобразованной САУ с АИМ при за-
данном значении
и
η
, является линией равной степени устойчивости
исходной системы. Таким образом, исследование степени устойчи-
вости исходной САУ с АИМ сводится к исследованию устойчиво-
сти преобразованной системы с помощью, например, аналогов
критериев устойчивости, изложенных в разделе 10.2.
qIm
2
q
4
q
1
q 0 qRe
5
q
3
q
и
η
Рис. 11.4. Определение степени
у
стойчивости
q
