Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

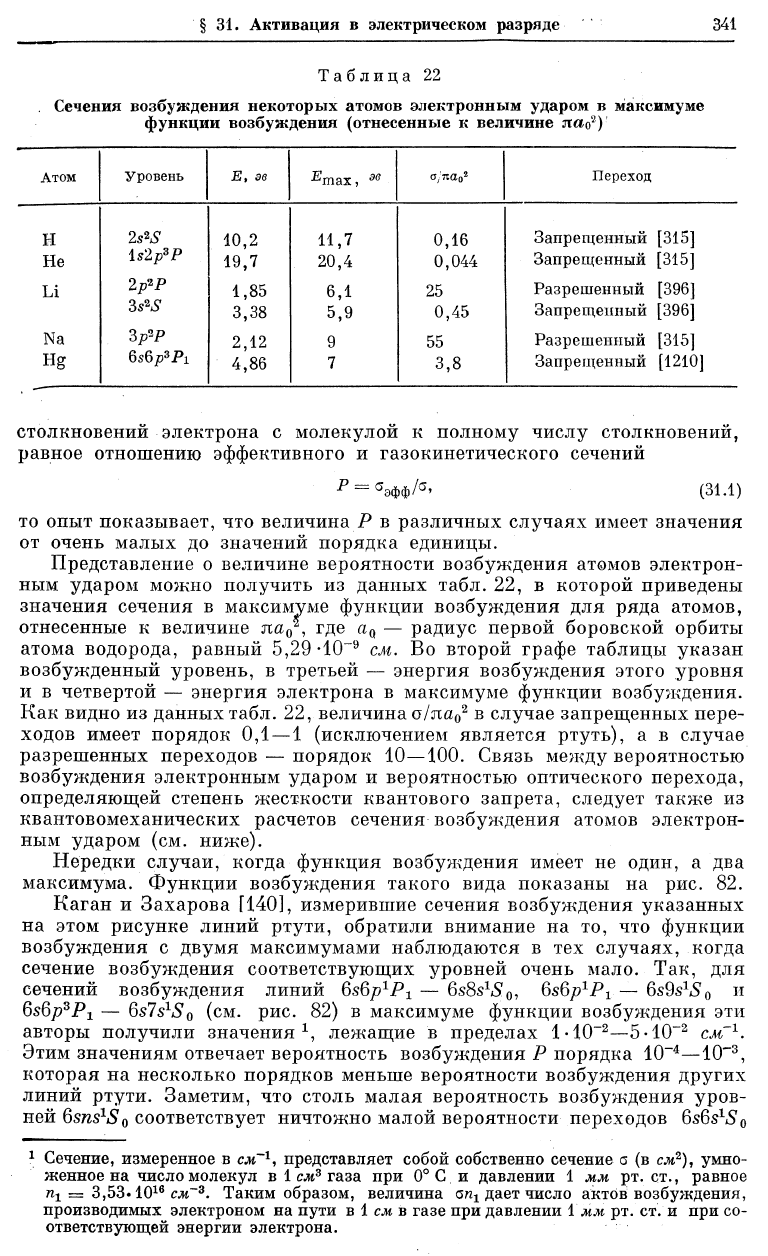
Таблица 22

Сечения возбуждения некоторых атомов электронным ударом в максимуме

функции возбуждения (отнесенные к величине яа

)

Атом

Уровень

E, эв

max,

эв

a/nao

Переход

Не

\s2p

10,2

19,7

11,7

20,4

0,16

0,044

Запрещенный [315]

1,85

3,38

6,1

5,9

0,45

Разрешенный [396]

Запрещенный [396]

3 p

6s6 p

P±

2,12

4,86

3,8

Разрешенный [315]

Запрещенный [1210]

столкновений электрона с молекулой к полному числу столкновений,

равное отношению эффективного и газокинетического сечений

р==:с?

эфф/

> (31.1)

то опыт показывает, что величина Р в различных случаях имеет значения

от очень малых до значений порядка единицы.

Представление о величине вероятности возбуждения атомов электрон-

ным ударом можно получить из данных табл. 22, в которой приведены

значения сечения в максимуме функции возбуждения для ряда атомов,

отнесенные к величине ла

, где a

— радиус первой боровской орбиты

атома водорода, равный 5,29-10"*

см. Во второй графе таблицы указан

возбужденный уровень, в третьей — энергия возбуждения этого уровня

и в четвертой — энергия электрона в максимуме функции возбуждения.

Как видно из данных табл. 22, величина с/ка

в случае запрещенных пере-

ходов имеет порядок

0,1 — 1

(исключением является ртуть), а в случае

разрешенных переходов — порядок 10—100. Связь между вероятностью

возбуждения электронным ударом PI вероятностью оптического перехода,

определяющей степень жесткости квантового запрета, следует также из

квантовомеханических расчетов сечения возбуждения атомов электрон-

ным ударом (см. ниже).

Нередки случаи, когда функция возбуждения имеет не один, а два

максимума. Функции возбуждения такого вида показаны на рис. 82.

Каган и Захарова [140], измерившие сечения возбуждения указанных

на этом рисунке линий ртути, обратили внимание на то, что функции

возбуждения с двумя максимумами наблюдаются в тех случаях, когда

сечение возбуждения соответствующих уровней очень мало. Так, для

сечений возбуждения линий QsQp

— 6s8s

, 6s6p

— 6$9А!?о и

б^б/?

^ — 657Л?

(см. рис. 82) в максимуме функции возбуждения эти

авторы получили значения

, лежащие в пределах 1

•

10~

—5

•

10~

см"

Этим значениям отвечает вероятность возбуждения Р порядка 10~

—10~

которая на несколько порядков меньше вероятности возбуждения других

линий ртути. Заметим, что столь малая вероятность возбуждения уров-

ней Gsns^-So соответствует ничтожно малой вероятности переходов бзбя

Сечение, измеренное в см"

, представляет собой собственно сечение а (в см

), умно-

женное на число молекул в 1 см

газа при 0° С и давлении 1 мм рт. ст. , равное

= 3,53* 10

см~

. Таким образом, величина сп

дает число актов возбуждения,

производимых электроном на пути в 1 см в газе при давлении 1 мм рт. ст. и при со-

ответствующей энергии электрона.

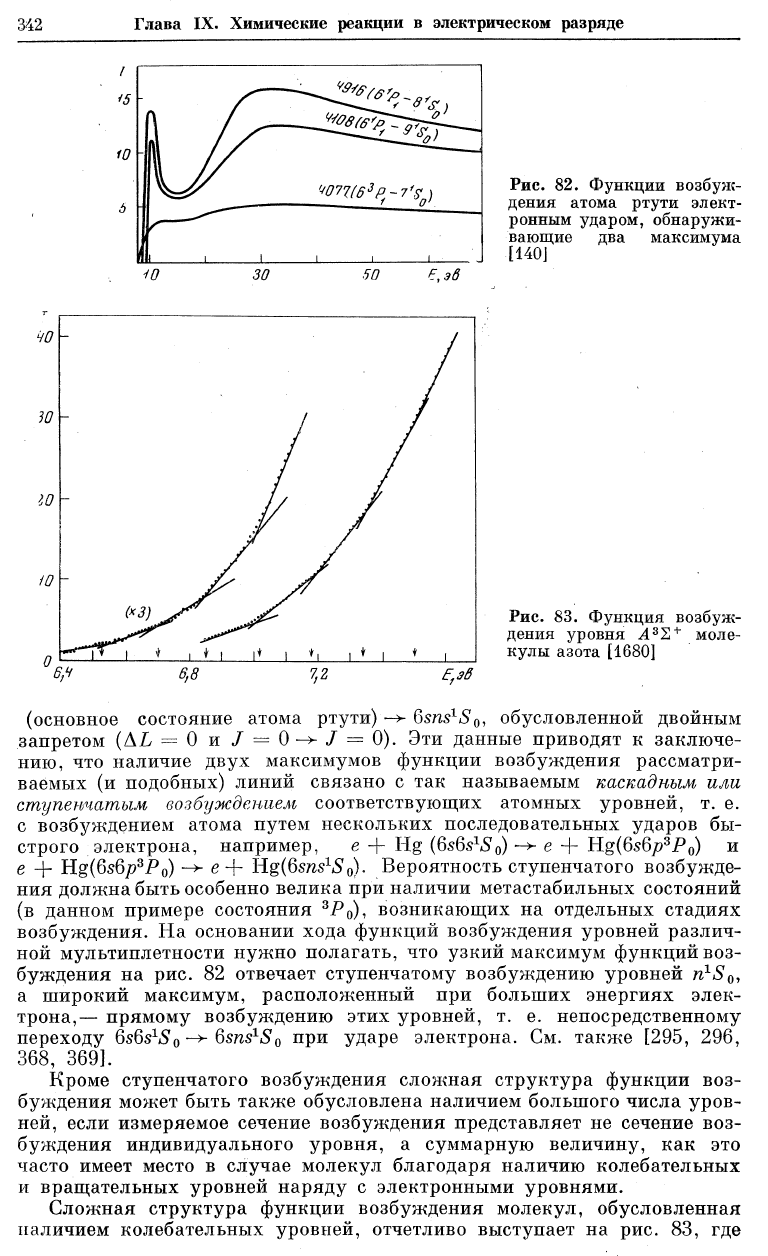
Рис. 82. Функции возбуяс-

деиия атома ртути элект-

ронным ударом, обнаружи-

вающие два максимума

[140]

6, I

Рис. 83. Функция возбуж-

дения уровня моле-

кулы азота [1680]

(основное состояние атома ртути) -+Qsns

, обусловленной двойным

запретом (AL = 0 и / = 0 / = 0). Эти данные приводят к заключе-

нию, что наличие двух максимумов функции возбуждения рассматри-

ваемых (и подобных) линий связано с так называемым каскадным или

ступенчатым возбуждением соответствующих атомных уровней, т. е.

с возбуждением атома путем нескольких последовательных ударов бы-

строго электрона, например, е + Hg (6s6s

) е + Hg(6s6/?

) и

е + Hg(6s6p

) е + Hg{6sns

Sо)

•

Вероятность ступенчатого возбужде-

ния должна быть особенно велика при наличии метастабильных состояний

(в данном примере состояния

), возникающих на отдельных стадиях

возбуждения. На основании хода функций возбуждения уровней различ-

ной мультиплетности нужно полагать, что узкий максимум функций воз-

буждения на рис. 82 отвечает ступенчатому возбуждению уровней тг

а широкий максимум, расположенный при больших энергиях элек-

трона,— прямому возбуждению этих уровней, т. е. непосредственному

переходу 6sQs

—6sns

при ударе электрона. См. также [295, 296,

368, 369].

Кроме ступенчатого возбуждения сложная структура функции воз-

буждения может быть также обусловлена наличием большого числа уров-

ней, если измеряемое сечение возбуждения представляет не сечение воз-

буждения индивидуального уровня, а суммарную величину, как это

часто имеет место в случае молекул благодаря наличию колебательных

и вращательных уровней наряду с электронными уровнями.

Сложная структура функции возбуждения молекул, обусловленная

наличием колебательных уровней, отчетливо выступает на рис. 83, где

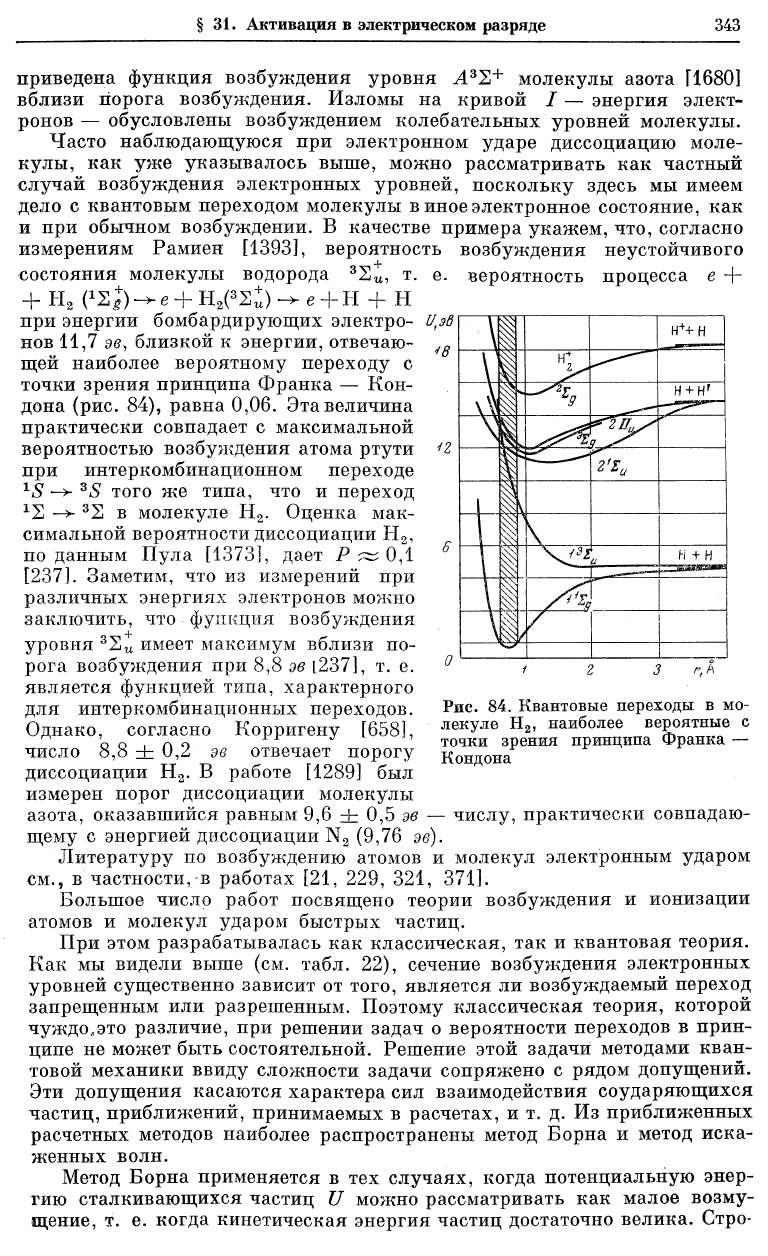
приведена функция возбуждения уровня A

молекулы азота [1680]

вблизи порога возбуждения. Изломы на кривой / — энергия элект-

ронов — обусловлены возбуждением колебательных уровней молекулы.

Часто наблюдающуюся при электронном ударе диссоциацию моле-

кулы, как уже указывалось выше, можно рассматривать как частный

случай возбуждения электронных уровней, поскольку здесь мы имеем

дело с квантовым переходом молекулы в иное электронное состояние, как

и при обычном возбуждении. В качестве примера укажем, что, согласно

измерениям Рамиен [1393], вероятность возбуждения неустойчивого

вероятность процесса

состояния молекулы водорода

+ Н

(^^е + Я^Ю^е+Я -f

при энергии бомбардирующих электро- и^В

нов 11,7 эв, близкой к энергии, отвечаю-

щей наиболее вероятному переходу с

точки зрения принципа Франка — Кон-

дона (рис. 84), равна 0,06. Эта величина

практически совпадает с максимальной

вероятностью возбуждения атома ртути

при интеркомбинационном переходе

S того же типа, что и переход

2 в молекуле Н

. Оценка мак-

симальной вероятности диссоциации Ы

поданным Пула [1373], дает Р ж 0,1

[237]. Заметим, что из измерений при

различных энергиях электронов можно

заключить, что функция возбуждения

уровня

имеет максимум вблизи по-

рога возбуждения при 8,8 эв [237], т. е.

является функцией типа, характерного

для интеркомбинационных переходов.

Однако, согласно Корригену [658],

число 8,8 ± 0,2 эв отвечает порогу

диссоциации Ы

. В работе [1289] был

измерен порог диссоциации молекулы

азота, оказавшийся равным 9,6 + 0,5 эв

щему с энергией диссоциации N

(9,76 эв).

Литературу по возбуждению атомов и молекул электронным ударом

см., в частности, в работах [21, 229, 321, 371].

Большое число работ посвящено теории возбуждения и ионизации

атомов и молекул ударом быстрых частиц.

При этом разрабатывалась как классическая, так и квантовая теория.

Как мы видели выше (см. табл. 22), сечение возбуждения электронных

уровней существенно зависит от того, является ли возбуждаемый переход

запрещенным или разрешенным. Поэтому классическая теория, которой

чуждо,это различие, при решении задач о вероятности переходов в прин-

ципе не может быть состоятельной. Решение этой задачи методами кван-

товой механики ввиду сложности задачи сопряжено с рядом допущений.

Эти допущения касаются характера сил взаимодействия соударяющихся

частиц, приближений, принимаемых в расчетах, и т. д. Из приближенных

расчетных методов наиболее распространены метод Ворна и метод иска-

женных волн.

Метод Ворна применяется в тех случаях, когда потенциальную энер-

гию сталкивающихся частиц U можно рассматривать как малое возму-

щение, т. е. когда кинетическая энергия частиц достаточно велика. Стро-

Рис. 84. Квантовые переходы в мо-

лекуле Н

, наиболее вероятные с

точки зрения принципа Франка —

Кондона

числу, практически совпадаю-

гое рассмотрение этого вопроса (см., например, [207, § 45]) приводит к

заключению, что указанное предположение законно при выполнении

следующего условия:

1^шах| (31.2)

где а — линейный размер области, в которой U заметно отличается от

нуля; и — скорость относительного движения.

Решение задачи неупругого столкновения электрона с атомом в бор-

новском приближении приводит к следующему выражению для диффе-

ренциального сечения:

de — 8л;

Здесь

е*

Ни

(31.3)

. Р

. (РУ

РР'

где р и р' — начальное и конечное значение импульса электрона; ф —

угол рассеяния; г

— радиус-вектор Z-ro электрона в атоме; ij)

и —

волновые функции, характеризующие начальное и конечное состояния

системы; интегрирование по т означает интегрирование по координатам

всех электронов атома.

Заметим, что ввиду того, что выражение (31.3) не содержит масс

сталкивающихся частиц, оно применимо как к электронам, так и к лю-

бым заряженным частицам.

Можно также показать [207], что если q имеет порядок величины ли-

нейного размера атома, то для о выполняется следующее приближенное

равенство:

= const ДЛ (31.4)

Из теории взаимодействия частиц при их соударениях может быть

получена наблюдаемая на опыте связь между вероятностью возбуждения

при электронном ударе и вероятностью соответствующего оптического

перехода. Вычисляя сечение возбуждения квантового перехода i /

ударом электрона в борновском приближении, можно представить вели-

чину Oij в виде ряда, каждый из членов которого оказывается соответ-

ственно пропорциональным квадрату матричного элемента [240],

I4I

§ V4*dt|

(31.5)

(г — координата электрона, % и % — волновые функции атома в со-

стояниях i и /), определяющего вероятность (интенсивность) оптического

перехода / ->• i при дипольном (s — 1), квадрупольном (s = 2) и т. д. из-

лучении. При этом в случае незапрещенных оптических переходов

(s = 1) в выражении для сг^ можно пренебречь всеми членами, кроме

первого, вследствие чего сечение возбуждения будет пропорционально

величине:

(31.6)

т. е. квадрату матричного элемента, отвечающего диполъному излучению.

Если же данный оптический переход запрещен ([г^|

= 0), сечение воз-

буждения при электронном ударе будет определяться матричным эле-

ментом, отвечающим квадруполъному излучению. Следовательно, вероят-

ность возбуждения данного уровня электронным ударом должна быть

пропорциональна вероятности соответствующего оптического перехода.

При малых значениях относительной скорости и, когда борновское

приближение неприменимо, может быть применен метод искаженных волн.

Сущность этого метода состоит в следующем. В отличие от метода Борна,

в котором электрон рассматривается как свободно движущаяся частица,

в методе искаженных волн в волновые уравнения вводится средняя энер-

гия атомного поля, в котором находится электрон до его столкновения с

атомом U

= ^tynUtyndx и после столкновения U

> = JilvZ/ijvdT.

Получающееся в этом случае выражение для дифференциального сече-

ния имеет вид:

d<5

= 2л

"f" I

(Г)

sin ftdft, (31.7>

где %

и %

> — волновые функции электрона до и после столкновения;

интегрирование по т' означает интегрирование по координатам бомбар-

дирующего электрона.

0,5

i Ч 7 Е

Рис. 85. Сравнение с опытом рассчитанных эффективных сечений (в атомных едини-

цах) возбуждения перехода Is — 2р в атоме водорода электронным ударом (энергия

выражена в единицах порога возбуждения)

1 — борновское приближение; 2 — метод искаженных] волн; з — метод, учитывающий взаимное

отталкивание электронов; точки — экспериментальные данные, согласно [1383]

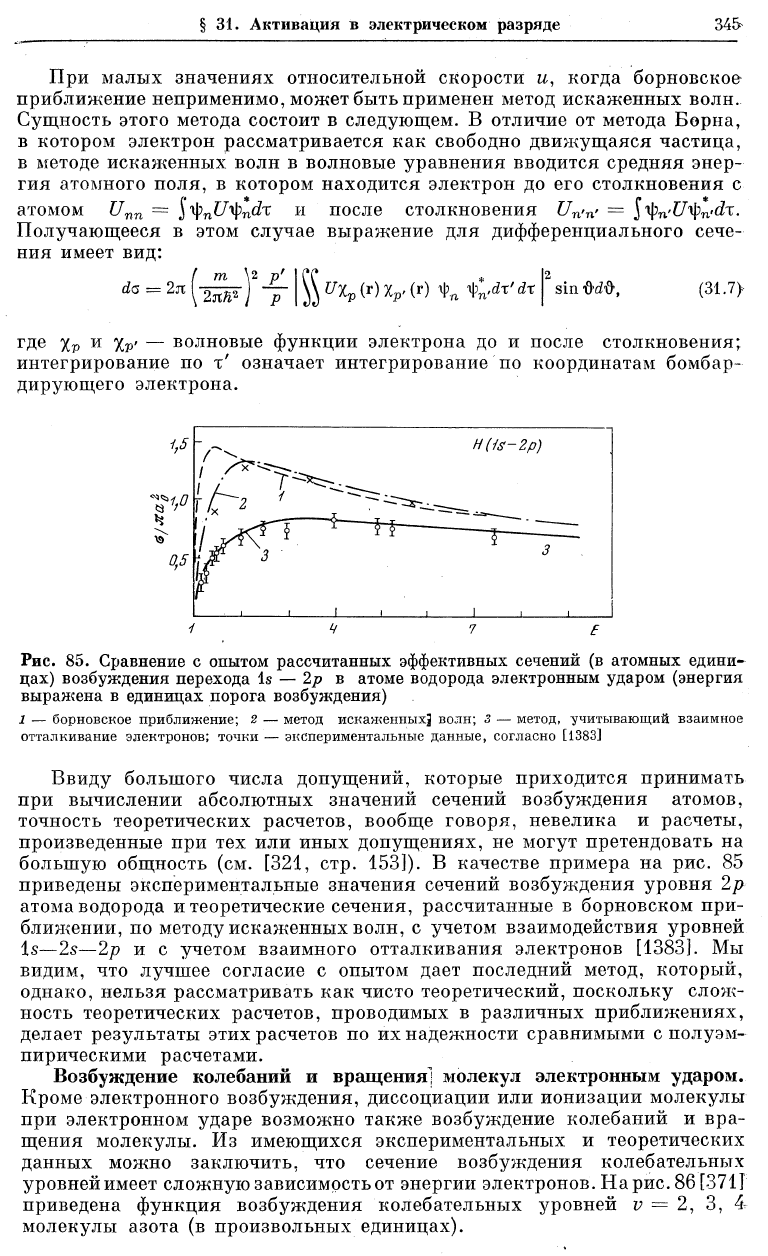
Ввиду большого числа допущенрш, которые приходится принимать

при вычислении абсолютных значений сечений возбуждения атомов,

точность теоретических расчетов, вообще говоря, невелика и расчеты,

произведенные при тех или иных допущениях, не могут претендовать на

большую общность (см. [321, стр. 153]). В качестве примера на рис. 85

приведены экспериментальные значения сечений возбуждения уровня 2р

атома водорода и теоретические сечения, рассчитанные в борновском при-

ближении, по методу искаженных волн, с учетом взаимодействия уровней

Is—2s-—2р и с учетом взаимного отталкивания электронов [1383]. Мы

видим, что лучшее согласие с опытом дает последний метод, который,

однако, нельзя рассматривать как чисто теоретический, поскольку слож-

ность теоретических расчетов, проводимых в различных приближениях,

делает результаты этих расчетов по ихнадеяшости сравнимыми с полуэм-

пирическими расчетами.

Возбуждение колебаний и вращения] молекул электронным ударом.

Кроме электронного возбуждения, диссоциации или ионизации молекулы

при электронном ударе возможно также возбуждение колебаний и вра-

щения молекулы. Из имеющихся экспериментальных и теоретических

данных можно заключить, что сечение возбуждения колебательных

уровней имеет сложную зависимость от энергии электронов. На рис. 86 [3711

приведена функция возбуждения колебательных уровней v = 2, 3, 4

молекулы азота (в произвольных единицах).

Шульц [1456] измерил сечение возбуждения электронным ударом

первого колебательного уровня молекулы водорода, оказавшееся рав-

ным (при энергии электрона, на 0,1 эв превышающей энергию возбужде-

ния 0,53 эе) величине порядка 10~

см

. Сечение близкого порядка ве-

личины было получено также для молекулы кислорода [371].

Однако при энергии электронов, существенно превышающей энер-

гию возбуждаемого уровня, сечение возбуждения колебаний оказывается

на несколько порядков большим. Так, при энергии 2 эв сечение возбуж-

дения уровня v = 1 молекулы Н

, согласно [371], равно ~ 6-10~

см

и уровня ,7 = 2 — 1 -Ю"

сж

. См. также [674, 916, 917, 1393].

Заметим, что для соударения упругих шаров

из-за неблагоприятного соотношения масс доля

кинетической энергии электрона, переходящая

в колебательную (и вращательную) энергию мо-

лекулы, ничтожно мала; поэтому с точки зрения

этой модели при электронном ударе не должно

иметь места ни возбуяедение колебаний, ни вра-

>щения молекулы (имеются в виду медленные элек-

Iтроны).

Наблюдаемое возбуждение колебанийука-

°зывает на неприменимость простой механической

модели к этому процессу. Франк [799] предло-

жил механизм возбуждения колебаний молекулы

при электронном ударе, в основе которого лежит

представление о том, что электрон при сближении

с молекулой сильно искажает ее внутреннее поле

и тем самым изменяет взаимодействие атомов в

^ молекуле, вследствие чего и может произойти из-

уЭ

менение ее колебательного состояния.

Рис. 86. Функции воз- Конкретный механизм возбуждения колебаний

Суждения колебательных при электронном ударе, по существу являющий-

уровней v^y 2 (a),v=

ся

развитием идеи Франка, был постулирован

(

2о4"элек.то™ Хаасом [900] (см. также [632, 1208, 1457-1460]),

ударом [371, стр. 301] который нашел, что при энергии электронов

2 эв сечение возбуждения колебаний молекулы N

имеет максимум, причем при одном ударе возбуждается несколько коле-

бательных квантов, что Хаас связывает с образованием короткоживу-

щего иона N

. Согласно Хаасу, максимальное сечение возбуждения коле-

баний N

составляет 3 -10~

см

. Данные Хааса позднее получили под-

тверждение в работах Шульца [1458, 1459]. Таким образом, механизм

возбуждения колебаний N

, согласно этим авторам, заключается в об-

разовании неустойчивого иона N

(с максимальной вероятностью при

2,3 эв), распадающегося на электрон и молекулу N

, которая может нахо-

диться на различных колебательных уровнях.

e + +е. (31.8)

Шульц нашел, что аналогичному механизму следует также возбуж-

дение колебаний молекул СО (максимум при 1,7 эв) и N

0. В последнем

случае наряду с процессом образования колебательно-возбужденной

молекулы N

е + N

0 — N

0" — N

0* + е

имеет место также процесс

Е,эв

в котором образуется колебательно-возбужденная молекула N

и ста-

бильный ион О". Максимум сечения приходится на 0,7 ± 0,1 эв и соот-

ветственно 2,23 ± 0,1 эв.

Кроме непосредственного возбуждения колебаний молекул при

электронном ударе, существуют косвенные пути образования колеба-

тельно-возбужденных молекул в электрическом разряде. Например,

такие молекулы могут возникнуть при электронном возбуждении

неколеблющейся молекулы с последующим ее оптическим переходом

в основное электронное состояние, как это показано на рис. 87.

Далее колебательно- или вращательно-возбужденная частица может

возникнуть в результате диссоциации молеку-

лы при электронном ударе. Одним из ярких

примеров вращательного возбуждения при

диссоциации молекулы является гидроксил,

образующийся в процессе е + Н

0 = Н +

+ ОН + е. На основании законов сохранения

можно показать [169], что в этом случае вра-

щательная энергия ОН может достигать очень

больших значений, намного превосходящих

средние значения, отвечающие равновесию.

В соответствии с этим измерения «вращатель-

ной температуры» возбужденных молекул ОН

возникающих в электрическом разряде в па-

рах воды (при низких давлениях), дают для

величину порядка 10 000°. Имеются также

указания, что колебательно-возбужденные час-

тицы могут возникать в результате перезаряд-

ки ионов [926, 1158], а также в результате вто-

ричных процессов химического взаимодействия

образующихся при электронной бомбардировке

положительных ионов с нейтральными молеку-

лами. К такому заключению приводят, в част-

ности, данные Франкевича (см. [338, 340, 367]), изучавшего вторич-

ные процессы типа Н

+ Н

0 = Н

+ ОН. Наконец, колебательно-

и вращательно-возбужденные молекулы образуются также при рекомби-

нации атомов и радикалов.

Квантовомеханический расчет сечения возбуждения колебаний моле-

кулы водорода при электронном ударе, учитывающий кулоновское взаи-

модействие возбуждающего электрона с электронами и ядрами молекулы

, был выполнен Та Ю-Ву 11565]. См. также 1614]. Сечение возбуждения

колебательного кванта молекулы водорода при энергии электронов в

несколько электронвольт, согласно вычисленной автором функции воз-

буждения, составляет ~ 0,5 -10"

см

. Это число оказывается на порядок

меньше измеренного Рамиеном [1393] для Е

эл

= 3,5 ч- 7,0 эв.

Теория возбуждения колебаний применительно к механизму е + N

—>

->• N

Nj + в была дана Ченом [631]. См. также [633, 948]. Вычис-

ленные Ченом сечения возбуждения в максимумах функции возбуждения

первых колебательных квантов молекулы N

имеют порядок величины

10~

см

(измеренное Хаасом [900] максимальное сечение равно 3 -10"

см

Вычисленный Ченом ход парциальных сечений возбуждения различных

колебательных уровней находится в хорошем согласии с результатами

измерений Шульца.

колебательно-возбужденной

молекулы в основном со-

стоянии через электронное

возбуждение при ударе бы-

строго электрона

Интересно отметить, что столь высокие «вращательные» температуры не возникают

при возбуждении гидроксила водородными каналовыми лучами [985].

Что касается возбуждения вращения молекулы, то, насколько об этом

можно судить по распределению интенсивности в полосах возбуждаемых

в электрическом разряде электронных спектров, при ударе быстрого

электрона вращательная энергия молекул изменяется очень мало. Од-

нако при энергии электронов порядка 1 эв вероятность возбуждения

вращения становится значительной, как это явствует из опытов по ис-

следованию замедления электронов в различных газах [237, 407, 674,.

928]. Из этих опытов, в частности, следует, что если в случае Не, Ne и Аг

средняя потеря энергии при соударении электрона с атомом в соответ-

ствии' с теорией упругого удара отвечает 2т

-Е1т, то в молекуляр-

ных газах потери значительно превышают эту величину. К этому

результату приводят также и теоретические данные [614, 840, 841,

1207, 1538, 1565]. Так, Месси [1207] вычислил сечение возбуждения вра-

щения полярной молекулы ударом электрона; из его расчета следует, что

потери энергии электронов в этом случае значительно превышают потери

при упругих соударениях. Герджой и Стейн Г840] для сечения возбуж-

дения вращательных уровней двухатомной неполярной молекулы в бор-

цовском приближении в предположении дальнодействующего взаимо-

действия электрона с молекулой получили следующее выражение:

_ 8я0_ (/ + !)(/ + 2) Г 2Во(2/+3) IV.

15 (2/ + 1) (2/ + 3) [_ 2?

эл

j •

где — квадрупольный момент молекулы; Б

— вращательная постоян-

ная; 7 — вращательное квантовое число.

Расчеты по этой формуле показывают, что доля передаваемой энер-

гии значительно превышает долю, вычисляемую из теории упругого уда-

ра. В случае азота обе величины различаются на целый порядок. Стейн,

Герджой и Голштейн [1538] нашли, что при энергии электронов, боль-

шей по сравнению с расстоянием между вращательными уровнями, се-

чение возбуждения вращения молекулы азота должно быть величиной

порядка 10~

см

(величина Р порядка 10~

). Для молекулы Н

расчеты

Герджой и Стейна [841] дают худшее, чем для N

, согласие между вычис-

ленными и измеренными значениями потерь энергии электрона при столк-

новении с молекулой (см. также [614]). Вычисленные потери оказываются

ниже полученных из опыта.

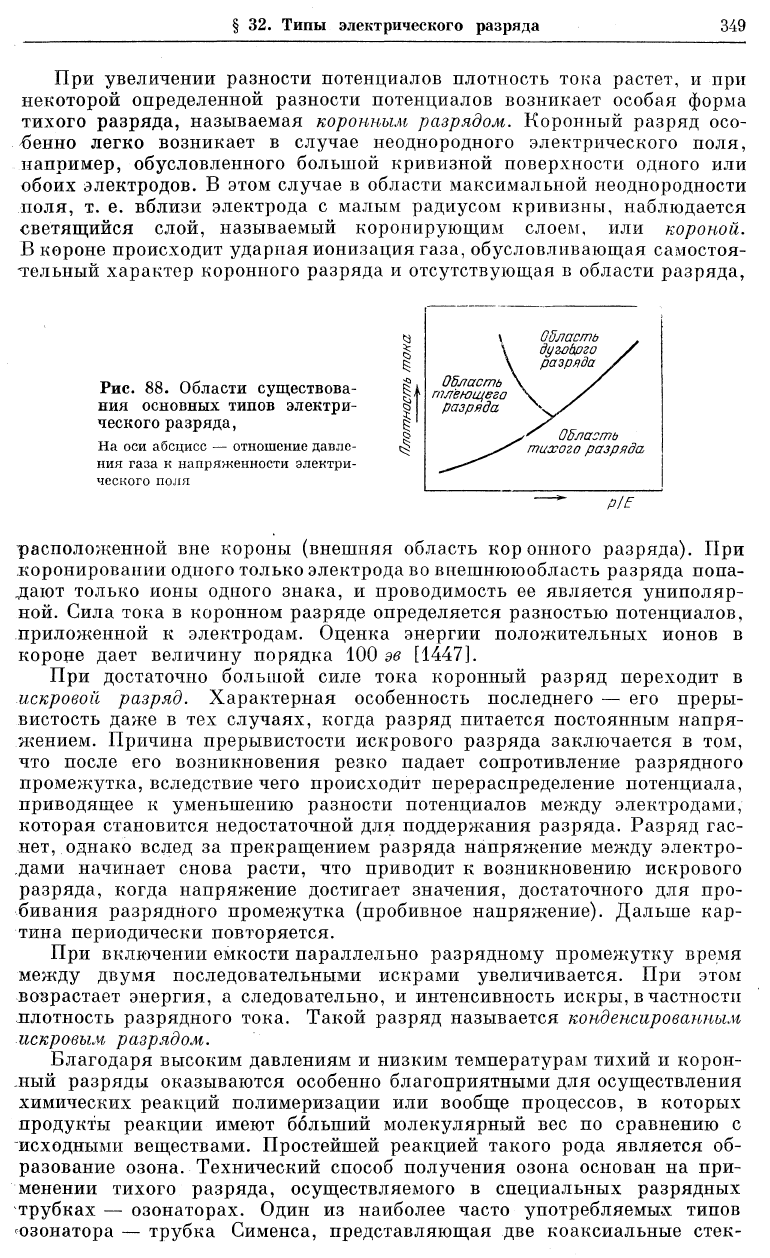
§ 32. ТИПЫ ЭЛЕКТРИЧЕСКОГО РАЗРЯДА

Тихий разряд. Искровой разряд

Воздействие электрического разряда на химические вещества зависит

от характера разряда, который определяется в первую очередь разностью

потенциалов, давлением в зоне разряда и плотностью тока. Различают

три основных типа электрического разряда: тихий, тлеющий и дуговой.

На рис. 88 схематически показаны области существования этих основных

типов разряда. Здесь по оси абсцисс отложена величина отношения дав-

ления в зоне разряда к напряженности электрического поля, а по оси

ординат — плотность разрядного тока. При изменении этих параметров

один тип разряда переходит в другой. Тихий разряд, обычно наблюдаю-

щийся при давлениях порядка атмосферного и сравнительно высоких

разностях потенциалов между электродами, представляет собой само-

стоятельный разряд, обусловленный проводимостью газа за счет его

остаточной ионизации. В соответствии с этим тихий разряд характери-

зуется малой плотностью тока и связанным с нею отсутствием влияния

объемных зарядов.

При увеличении разности потенциалов плотность тока растет, и при

некоторой определенной разности потенциалов возникает особая форма

тихого разряда, называемая коронным разрядом. Коронный разряд осо-

бенно легко возникает в случае неоднородного электрического поля,

например, обусловленного большой кривизной поверхности одного или

обоих электродов. В этом случае в области максимальной неоднородности

поля, т. е. вблизи электрода с малым радиусом кривизны, наблюдается

светящийся слой, называемый короиирующим слоем, или короной.

В короне происходит ударная ионизация газа, обусловливающая самостоя-

тельный характер коронного разряда и отсутствующая в области разряда,

расположенной вне короны (внешняя область коронного разряда). При

коронировании одного только электрода во внешнююобласть разряда попа-

дают только ионы одного знака, и проводимость ее является униполяр-

ной. Сила тока в коронном разряде определяется разностью потенциалов,

приложенной к электродам. Оценка энергии положительных ионов в

короне дает величину порядка 100 эв [1447].

При достаточно большой силе тока коронный разряд переходит в

искровой разряд. Характерная особенность последнего — его преры-

вистость даже в тех случаях, когда разряд питается постоянным напря-

жением. Причина прерывистости искрового разряда заключается в том,

что после его возникновения резко падает сопротивление разрядного

промежутка, вследствие чего происходит перераспределение потенциала,

приводящее к уменьшению разности потенциалов между электродами,

которая становится недостаточной для поддержания разряда. Разряд гас-

нет, однако вслед за прекращением разряда напряжение между электро-

дами начинает снова расти, что приводит к возникновению искрового

разряда, когда напряжение достигает значения, достаточного для про-

бивания разрядного промежутка (пробивное напряжение). Дальше кар-

тина периодически повторяется.

При включении емкости параллельно разрядному промежутку время

между двумя последовательными искрами увеличивается. При этом

возрастает энергия, а следовательно, и интенсивность искры, в частности

плотность разрядного тока. Такой разряд называется конденсированным

искровым.; разрядом.

Благодаря высоким давлениям и низким температурам тихий и корон-

ный разряды оказываются особенно благоприятными для осуществления

химических реакций полимеризации или вообще процессов, в которых

продукты реакции имеют больший молекулярный вес по сравнению с

"исходными веществами. Простейшей реакцией такого рода является об-

разование озона. Технический способ получения озона основан на при-

менении тихого разряда, осуществляемого в специальных разрядных

трубках — озонаторах. Один из наиболее часто употребляемых типов

озонатора — трубка Сименса, представляющая две коаксиальные стек-

На оси абсцисс — отношение давле-

ния газа к напряженности электри-

ческого поля

Рис. 88. Области существова-

ния основных типов электри-

ческого разряда,

Р/Е

лянные трубки с проводящими обкладками (рис. 89). Пропуская кисло-

род (или воздух) через промежуток между трубками, в отходящем газе

получают то или иное содержание озона.

Вследствие высокого напряжения и большой плотности тока в искро-

вом канале конденсированной искры этот вид разряда особенно приго-

ден для осуществления процессов глубокого расщепления молекул,

сопряженного с затратой больших порций энергии. Так, например

конденсированный разряд дает особенно большие выходы атомарного

азота, получающегося в результате расщепления молекул N

, которые

принадлежат к числу наиболее прочных молекул.

Тлеющий разряд обычно наблюдается при давлении в несколько де-

сятков миллиметров ртутного столба и ниже, хотя при соблюдении оп-

ределенных условий, в частности при охлаждении катода, этот тип разряда

можно получить и при атмосферном давлении. Для тлеющего разряда

характерно своеобразное распределение свечения в промежутке между

электродами, отображающее соответствующее распределение потенциала.

Типичная картина распределения свечения и потенциала в тлеющем

разряде дана на рис. 90. Это распределение обусловлено следующим

механизмом разряда. Под влиянием ударов быстрых ионов из катода

вырываются электроны, которые ускоряются в сильном поле вблизи катода

(катодное падение потенциала). Это поле обусловлено двойным электри-

ческим слоем, образованным отрицательным зарядом катода и объемным

зарядом положительных ионов.

Ускоряясь, электроны получают способность возбуждать молекулы

газа при столкновении с последними. В результате возникает свечение,

имеющее форму тонкой пленки (катодное свечение), отделенной от катода

темным слоем (астоново темное пространство) и переходящей в слабо све-

тящийся слой (темное катодное пространство). Астоново темное простран-

ство, катодное свечение и темное катодное пространство занимают область

катодного падения потенциала, обычно составляющего 300 в!см [1537].

К этой области примыкает область отрицательного, или тлеющего свечения,

имеющего большую яркость. Предполагается, что в этой области проис-

ходит рекомбинация положительных ионов и электронов, а также воз-

буждение молекул газа, что и обусловливает большую яркость отрица-

тельного свечения. Заметим, что в спектре последнего преобладают по-

лосы, принадлежащие ионизованным молекулам (например, полосы N

СО

, 0

и т. д.), что свидетельствует о большой энергии бомбардирую-

щих электронов.

В области отрицательного свечения градиент потенциала резко па-

дает, иногда становясь отрицательным, что обусловлено диффузией мед-

ленных электронов, опережающих ионы, благодаря большему коэффи-

циенту диффузии. Отсутствие быстрых электронов в конце области

Рис. 89. Озонатор Сименса

Тлеющий разряд