Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

тивная константа скорости реакции

фф

= 10

ехр (—73063/i?7") сек'

При этом установили, что добавки окиси азота тормозят реакцию.

Позднее была измерена истинная константа скорости процесса С

= 2СН

, которая вблизи 575° С может быть представлена формулой к

ехр (—88

ООО/RТ)

сек"

11154]. Таким образом, при 575° С й

эфф

оказывается приблизительно в 20 раз больше Отношение &

<мДоо мож-

но, по-видимому, рассматривать как некоторую эффективную длину цепи

(20 звеньев при 575° С). Получающееся при этом уменьшение длины цепи

при повышении температуры может быть обусловлено квадратичным обры-

вом цепи (см. главу XI).

Рис. 57. Два пути изомерного

ц uc-mpanc-wp евращения

1 — без изменения мультиплетности

(I—1)\ 2 — с изменением мульти-

плетности (J—III—I).

U — потенциальная энергия моле-

кулы,

— угол поворота

Нередки также случаи, когда мономолекулярная реакция осуществля-

ется двумя или несколькими путями. Одним из простейших примеров такой

реакции является распад иодистого этила,

—ess:?'

Согласно [1702], константы скорости, отвечающие этим путям реакции,

равны: к

= Ю

ехр (-52 800/RT) и к

= 10

ехр (-50 000/RT) сек'

Очень часто сложный характер суммарной реакции проявляется в мак-

рокинетическом законе реакции. Так, например, кинетический закон ре-

акции термического распада дииодэтана C

[415] и втор-бутилиодида

J [1309] в определенном интервале давлений и температур описыва-

ется, соответственно, следующими уравнениями:

d [C2H4J2I

= Ai[CaH«J

] +

[C2H4J

]

[J2]

d [C4H9J]

••

/ci[C

J] +

[C4H9J] [J

]

В этих уравнениях первое слагаемое представляет скорость собственно

мономолекулярного процесса распада соответствующего иодида (т. е. ско-

рости процессов C

= C

J + J и C

J == С

+ J); второе сла-

гаемое — скорость вторичного процесса бимолекулярного взаимодействия

исходного иодида с образующимися в первичном процессе (а также при

диссоциации J

) атомами иода. Заметим, что при распаде дииодэтана взаи-

модействие атомов иода с C

представляет собой цепной процесс.

Необходимость тщательного исследования кинетики мономолекуляр-

ных реакций и осторожного подхода к интерпретации экспериментальных

фактов особенно наглядно иллюстрируется на примере разложения пяти-

окиси азота N

. Эта реакция, являющаяся первой известной гомогенной

мономолекулярной реакцией, обладает рядом аномалий, долгое время не

поддававшихся теоретическому истолкованию.

Одна ив аномалий состоит в том, что константа скорости реакции не за-

висит от давления N

вплоть до давлений порядка 0,1 мм рт. ст. С мо-

мента установления гомогенного характера этой реакции (Даниельс и

Джонстон [689]) ее исследованию было посвящено большое число работ, и

только сравнительно недавно была вскрыта причина ее аномального по-

ведения. Огг [1307] предложил механизм термического разложения пяти-

окиси азота, начинающегося с мономолекулярного распада N

по схеме

= N0

+ N0

, за которым следует ряд бимолекулярных процессов

(близкий к этому механизм был предложен Смитом и Даниельсом [1511]

для термического разложения N

в присутствии окиси азота N0). Со-

гласно этому механизму, нашедшему подтверждение в последующих ра-

ботах [964, 965, 1016, 1017, 1020, 1021, 1043, 1259, 1453], наблюдаемая при

низких давлениях константа скорости мономолекулярного распада явля-

ется кажущейся и в действительности представляет собой произведение

константы равновесия N

^ N0

+ N0

и константы скорости бимо-

лекулярного процесса N0

+ N0

= N0

+ NO + 0

, чем и объясняется

постоянство эффективной константы скорости мономолекулярного распада

при низких давлениях. На основании принятого механизма реакции

могут быть объяснены и другие аномалии термического разложения N

Как следует из теории мономолекулярных реакций, в отличие от вели-

чины

Аоо,

слабо зависящей от температуры, предэкспонент

в выражении

зависит от температуры в значительно большей степени (см. § 19). Так,

например, нужно ожидать, что для молекул, аппроксимируемых осцил-

ляторной моделью, предэкспонент А

при высоких температурах будет

зависеть от температуры, А

— y-s+vгде 5 — число степеней свободы

молекулы.

Ввиду неопределенностей, возникающих при построении модели актив-

ной молекулы, однозначное определение

теоретическим путем часто оказы-

вается невозможным. Поэтому обычно используется следующая формула:

где п — число, находимое из опыта, a D

— энергия разрываемой связи,

равная Е

. Вследствие малой точности измерений температурной зависи-

мости константы скорости при высоких температурах, полученные в раз-

личных работах величины п часто значительно расходятся между собой.

Так, по данным различных авторов значения п для константы ско-

рости диссоциации кислорода по реакции 0

+ 0

= О + О + 0

лежат

в пределах 1,5—3,0. Однако все полученные абсолютные значения кон-

станты, по-видимому, близки к истинным.

Можно убедиться в том, что вычисленные по формулам различных ав-

торов значения не более чем в 2 раза отличаются от значений, вычис-

ленных по формуле

в температурном интервале 3000—7000° К, в котором проводились измере-

ния [177].

Число п = 3 превышает максимально возможный для двухатомных мо-

лекул показатель п = 2, получающийся при допущении, что в активации

Предэкспоненциальный множитель в выражении ко

= А

ехр (— E

JRT)

(20.2)

молекулы 0

в процессе 0

+ 0

= О + О + 0

участвуют оба партнера

соударения. Возможное объяснение большого значения п состоит в следу-

ющем: если в активации молекулы кислорода при столкновениях 0

+ 0

основной вклад дает обмен колебательной энергии, то диссоциация может

вызвать понижение колебательной температуры. Это нарушение равновес-

ного распределения колебательной энергии на нижних уровнях, которое

отсутствует в случае системы двухатомная молекула — атом инертного

газа, может привести к дополнительной отрицательной температурной за-

висимости предэкспонента [194].

Константа к

нередко также выражается простой эмпирической форму-

лой Аррениуса

*о = ^эксп

ех

Р (-

эксп!

n (20.3)

где^экспИ.Е'эксп — величины, постоянные в определенном температурном

интервале.

Обозначив через Т температуру, при которой константы к

, вычисляе-

мые по формулам (20.2) и (20.3), совпадают, можно показать, что при

TjT = 2 эти значения различаются в 1,34^ раза при п = 2, в 1,62 раза при

п = 3 и в 1,97 раза при п — 4; при TIT —

различия составляют соот-

ветственно 1,58; 2,14 и 2,94 раза.

Обмен энергии в мономолекулярных реакциях. Константа скорости ре-

акции второго порядка к

зависит от природы партнера соударения, по-

скольку скорость активирующего соударения АВ + М = АВ * + М опре-

деляется взаимодействием частиц АВ и М. Ниже приведены относительные

эффективности активирующих столкновений различных газов в реакции

+ М - 2 ОН + М [178, стр. 316]

М Не Аг 0

N2 С0

0 Н

Относительная эффек-

тивность, а 0,55 0,67 0,75 1,00 1,24 4,8 6,0

Из этих данных следует, что наименьшей эффективностью обладают одно-

атомные гелий и аргон, наибольшей эффективностью — перекись водорода,

содержащая наибольшее число атомов. Однако в отличие от атомов инерт-

ных газов в реакциях типа А

+ М = А + А + М эффективность атомов

А превышает эффективность молекул А

, насколько об этом можно судить

по данным, относящимся к диссоциации молекул Н

, N

и 0

. Большая эф-

фективность атомов особенно ярко выражена в случае водорода, для кото-

рого в. области температур 3000—4500° К отношение > 20 [813].

Исследования мономолекулярных реакций дают ценные сведения о про-

цессах обмена энергии. В рамках допускаемых приближений теория моно-

молекулярных реакций позволяет оценить порядок величины вероятности

передачи энергии в процессах активации и дезактивации при молекуляр-

ных соударениях. Так, в случае осцилляторной модели мы имеем следую-

щее выражение для эффективной константы скорости к активационного

процесса:

(20.4)

(20.5)

(Р * — вероятность дезактивации при одном столкновении и Z

— частота

столкновений).

(Е ГкТ)

к = ko [М] = z

[М]

(

7_;

}

, ехр (- Е

/кТ),

где

z; = p*z

Как видно из приведенных выше формул для вычисления Р*, кроме

константы к

нужно знать входящие в выражение для этой константы

параметры Е

, s, а также диаметр молекулы d, входящий в выраже-

ние Z

Вычислим для примера вероятности дезактивации молекул N

и F

0. Согласно Джонстону [1016] , для N

Q при 888° К имеем ШМ] =

= 14,0 см

-моль"

•секПодставляя это число в формулу (20.4) и принимая

d = 3,2 -10~

см, Е

= 60 ккал, s = 4 и Т = 888 °К, найдем

Р* = 0,01. Что касается F

0, то из измеренной константы к [1084]

(Т — 523° К), d = 3,2 -10"

см, Е

= 40,6 ккал и s = 3 в этом случае по-

лучим Р* — 0,75

Таким образом, вероятность дезактивации активной молекулы F

оказывается на два порядка больше величины Р* для N

0. Это различие,

по-видимому, обусловлено тем, что величина колебательного кванта актив-

ной молекулы N

0 вследствие неадиабатического характера распада N

(см. [262, § 27, рис. 24]) велика, что не имеет места в случае адиабатичес-

кого процесса распада F

Предыдущие расчеты основаны на представлении о молекуле как гар-

моническом осцилляторе, что получает некоторое обоснование в следую-

щем. Ввиду того что энергия активной молекулы, т. е. энергия, необхо-

димая для ее мономолекулярного превращения, распределена между не-

сколькими колебательными степенями свободы (имеется в виду молекула,

состоящая более чем из двух атомов), можно предполагать, что колеба-

тельные квантовые числа соответствующих заселенных уровней невелики.

Это позволяет приближенно считать колебания активированной молекулы

гармоническими.

Рассмотрим, например, мономолекулярный распад N

0. В предположе-

нии, что энергия активации, составляющая ~ 60 ккал, распределена по-

ровну между всеми четырьмя колебательными степенями свободы, макси-

мальное значение колебательного квантового числа получим, разделив

15 ккал на энергию кванта, отвечающего наименьшей частоте 589 см'

(1,68

ккал): £>тах — 15/1,68 = 9. Экстраполируя далее величину

[1549,

стр. 211—212] к 900° К (температуре опытов по мономолекулярному раз-

ложению N

0), найдем для этой температуры

— 2 -10

и, следователь-

но, Р1, о

5 -10~

. Отсюда для вероятности дезактивации активированной

молекулы N

0 получим Р

9)8

= 4,5 -10"

. Это число по порядку величины

близко к вычисленной выше вероятности дезактивации активированной

молекулы N

0, Р* — 0,01.

Энергия активации мономолекулярных реакций

Из обширного опытного материала следует, что все процессы мономо-

лекулярного превращения в зависимости от соотношения между энергией

активации Е«, и тепловым эффектом реакции можно разделить на два клас-

са. К одному из этих классов относятся процессы, энергия активации ко-

торых превышает величину теплового эффекта. Таковы, в частности, ре-

акции цис-транс-изошершаащж, энергия активации которых составляет

десятки килокалорий при тепловом эффекте в несколько килокалорий.

Примером может служить изомеризация 1,2-диметилциклобутана, для ко-

торой константа скорости ^ис-т/?а«с-превращения выражается формулой

к = 10

>* ехр (— 60 100IRT) сек"

[839]. Путь мономолекулярной реакции

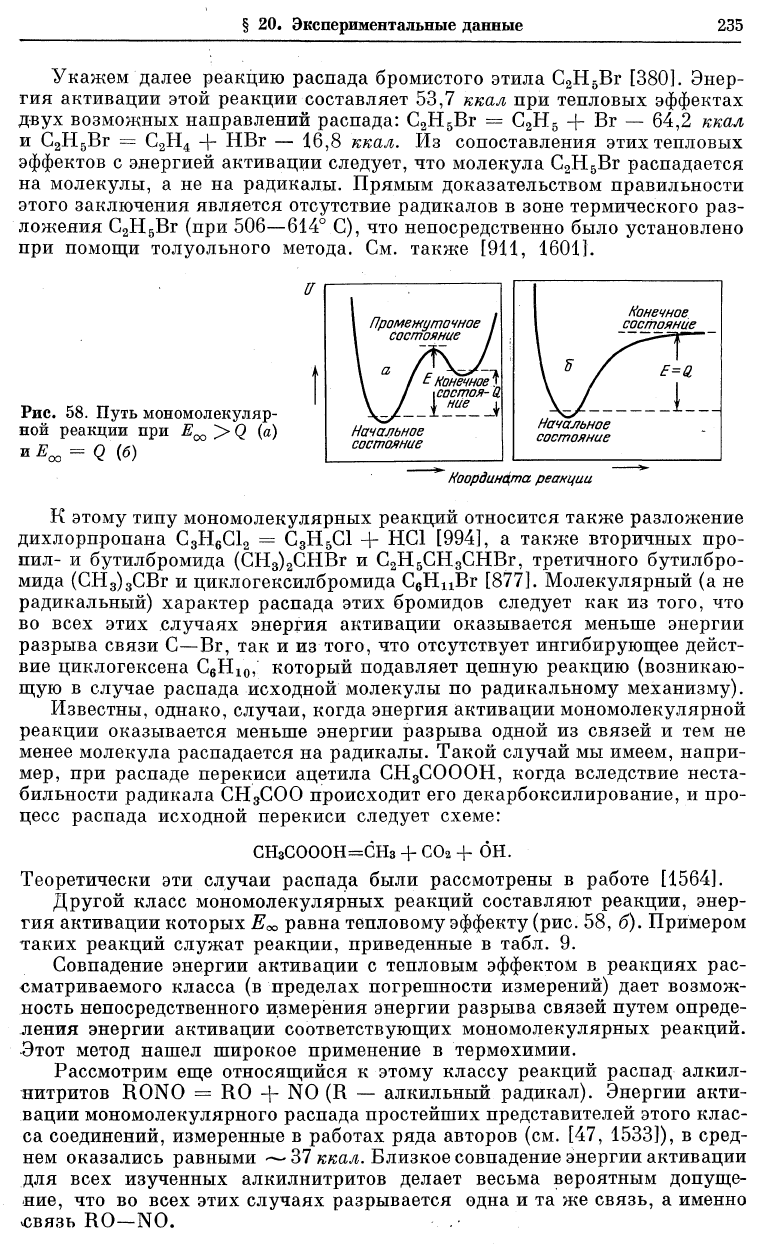
в этом случае может быть представлен рис. 58, а.

Хорошим примером мономолекулярной реакции рассматриваемого ти-

па является распад закиси азота N

0 = N

+ О — 38,7 ккал, энергия ак-

тивации которого равна 60,0 ккал.

Укажем далее реакцию распада бромистого этила С

Вг [380]. Энер-

гия активации этой реакции составляет 53,7 ккал при тепловых эффектах

двух возможных направлений распада: С

Вг = С

+ Вг — 64,2 ккал

и С

Вг = С

+ НВг — 16,8 ккал. Из сопоставления этих тепловых

эффектов с энергией активации следует, что молекула С

Вг распадается

на молекулы, а не на радикалы. Прямым доказательством правильности

этого заключения является отсутствие радикалов в зоне термического раз-

ложения С

Вг (при 506—614° С), что непосредственно было установлено

при помощи толуольного метода. См. также [911, 1601].

Рис. 58. Путь мономолекул ар-

ной реакции при Е^ > Q (а)

и^

= <?'(б)

HoopduHdma реакции

К этому типу мономолекулярных реакций относится также разложение

дихлорпропана С

С1

= С

С1 + НС1 [994], а также вторичных про-

пил- и бутилбромида (СН

)

СНВг и С

СН

СНВг, третичного бутилбро-

мида (СН

)

СВг и циклогексилбромида С

НцВг [877]. Молекулярный (а не

радикальный) характер распада этих бромидов следует как из того, что

во всех этих случаях энергия активации оказывается меньше энергии

разрыва связи С—Вг, так и из того, что отсутствует ингибирующее дейст-

вие циклогексена С

, который подавляет цепную реакцию (возникаю-

щую в случае распада исходной молекулы по радикальному механизму).

Известны, однако, случаи, когда энергия активации мономолекулярной

реакции оказывается меньше энергии разрыва одной из связей и тем не

менее молекула распадается на радикалы. Такой случай мы имеем, напри-

мер, при распаде перекиси ацетила СН

СОООН, когда вследствие неста-

бильности радикала СН

СОО происходит его декарбоксилирование, и про-

цесс распада исходной перекиси следует схеме:

СНзСОООН=СНз + С0

+ ОН.

Теоретически эти случаи распада были рассмотрены в работе [1564].

Другой класс мономолекулярных реакций составляют реакции, энер-

гия активации которых

Е<*>

равна тепловому эффекту (рис. 58, б). Примером

таких реакций служат реакции, приведенные в табл. 9.

Совпадение энергии активации с тепловым эффектом в реакциях рас-

сматриваемого класса (в пределах погрешности измерений) дает возмож-

ность непосредственного измерения энергии разрыва связей путем опреде-

ления энергии активации соответствующих мономолекулярных реакций.

Этот метод нашел широкое применение в термохимии.

Рассмотрим еще относящийся к этому классу реакций распад алкил-

нитритов RONO = RO + NO (R — алкильный радикал). Энергии акти-

вации мономолекулярного распада простейших представителей этого клас-

са соединений, измеренные в работах ряда авторов (см. [47, 1533]), в сред-

нем оказались равными — 37 ккал. Близкое совпадение энергии активации

для всех изученных алкилнитритов делает весьма вероятным допуще-

ние, что во всех этих случаях разрывается одна и та же связь, а именно

етязь RO—NO.

Т а б лица 9

Энергии активации Е^ реакций термического распада и энергии

разрываемых связей Q [47]

Разрываемая

связь

Еоо

1 g А*

Разрываемая

связь

Еоо

1 g А*

Разрываемая

связь

ккал

1 g А*

Разрываемая

связь

ккал

1 g А*

СНз—Н

102,4

103

CH3O-NO

37,7

34 12,9

СНз—СНз

" 86,&

16,3 NHa—NHa

58,4

CO—ОССНз

<69,6

67,2

NF2-NF2

19,1

19,4

15,0

СвНбСНз—•СНз

<72

69,2

14,7

—NO2

12,8 13,0 16,0

С2Н5—J <53

13,6

SF5-F 76

75,9

12,9s

* А выражено в сек-*.

Наряду с распадом на монорадикалы к этому же классу реакций отно-

сятся случаи распада молекул с образованием бирадикала, например, рас-

пад молекулы кетена СН

СО на СО и бирадикал СН

. Шилов и Сабирова

[381] в результате изучения термического распада СНС1

и CDC1

пришли к

заключению, что распад этих молекул протекает по схеме СНС1

= СС1

+ НС1. Константа скорости этого процесса выражается формулой к«, —

= 2,6 -10

ехр (—47

ООО/RT)

сек"

, тепловой эффект равен 53,7 + 10 ккал.

Вследствие отрицательной температурной зависимости предэкспонен-

циального множителя в выражении для константы скорости мономолеку-

лярной реакции второго порядка входящая в формулу Аррениуса,.

экспериментальная энергия активации Е

эксп

обычно оказывается сущест-

венно меньше величины Е

. Можно показать, что эти величины связаны

соотношением

Яэксп = (20.6)

где Т — средняя температура в изучаемом температурном интервале. Из

этой формулы следует, что при п = 2, 3 и4 и Т = 3500° К разность

— Яэксп составляет соответственно 10,5; 17,5 и 24,5 ккал.

В приведенном выше примере мономолекулярного распада С0

(§ 19)

разность Е

— £

ЭКС

п в температурном интервале 3000—4000° К составля-

ет — 25 ккал. Как мы видим, этой величине соответствует п — 4. С другой

стороны, из механизма сильных столкновений следует п — s — 1. Под-

ставляя сюда s = 4 (число колебательных степеней свободы С0

), полу-

чим п — 3. Это противоречие указывает на то, что активация С0

происхо-

дит по ступенчатому механизму.

Граница между областью низких и областью высоких давлений

Выше в качестве условной границы между этими областями было взято

давление /?i/

, при котором эффективная константа скорости к равна поло-

вине максимальной (коо).

Предельным случаем мономолекулярных реакций, скорость которых

следует закону второго порядка (константа скорости к

) еще при очень

высоких давлениях, является распад двухатомных молекул. Как указано

выше (§ 19), в этом случае состояния активной и активированной молекул

совпадают, так как двухатомная молекула немедленно диссоциирует, как

только ее энергия становится равной теплоте диссоциации; другими слова-

ми, время жизни активной молекулы является величиной порядка периода

колебаний. Давление рц

можно оценить, приравняв число столкновений

активной молекулы к обратному времени жизни. Взяв частоту столк-

см

-молекул

сек

и частоту колебаний равной

новении равной

АО

сек'

, получим LM]I/

= 10

молекул!см

или pv

~ 10 000 атм (Т

•= 500° С). Из этого расчета следует, что распад двухатомных молекул прак-

тически всегда является реакцией второго порядка.

Примером здесь может служить реакция 0

+ Аг = О + О + Аг,

изученная в температурном интервале 2850—18 000° К [1654, 1694, 1695].

Для температурного интервала 5000—18 000° К Рей [1694] приводит

два возможных выражения константы скорости: к = 2,5 -10

ехр (-118000/ЯГ) и к = 2,4

-10

Т'

ехр (—118 000/Л

Г)

см

-моль'

-сек'

Согласно Уотту и Майерсону [1654], в области температур 2850—5550° К

к = 5,01 -10

Г"

/* ехр (—118

000/RT).

Обращаясь к теоретической форму-

ле (19.35) и полагая йсо kТ, для температурной зависимости константы

скорости получаем:

к ~ g

(Т)

Г-i ехр (—118 000/ЯТ).

Как указывалось ранее, g

(Т) ~ Т

7-1

^ — 7

/*. Таким образом, предска-

зываемую теорией отрицательную температурную зависимость предэкспо-

нента константы скорости можно считать удовлетворительно согласующей-

ся с опытом.

В табл. 10 приведены значения

р^

измеренные для некоторых реакций.

Таблица 10

Измеренные значения p

для некоторых реакций

Реакция

Piy

, мм рт. ст.

0 + Аг =

+ О Аг

+.N.2

€

Нб — СНз + СНз

С2НбС1~,С2Н

НС1

Циклопропан —»СзН

Циклобутан 2G2H4

Метилциклопропан —»бутены

Диметилциклопропаы

—>

пен-

тены

2000

443

839

521

1000

723

763

754

000

100

4-6

0,15

0,2

0,03

Примечание. Литературу см. в работе [47].

Из данных этой таблицы отчетливо видна резкая зависимость величины

ру

от степени сложности молекулы: с увеличением числа атомов в молеку-

ле и, соответственно, с увеличением числа колебательных степеней свободы

область давлений, в которой удельная скорость реакции перестает зави-

сать от давления, все больше перемещается к малым давлениям.

Граница между областями высоких и низких давлений, pv

, в принципе

может быть получена также теоретическим путем на основании формулы

(19.22). Эту формулу, полученную для высоких температур, можно, одна-

ко, считать приближенно справедливой при любой температуре, если вмес-

то истинного числа колебательных степеней свободы s использовать $

фф

(очевидно,

фф

должно быть меньше

s).

Ввиду невозможности получить на-

Т{а^б[л и ц а 11

Значения «

эксп

и s для некоторых реакций [1614]

Реакция

EQQ,

ккал

Т, °К

9KCn

O-*N

+;О

61,1 888 3

ЖШ-*ГЮ

+ С1

29,5

500

4,5 6

СН

-> СНз + н

102

2000

7,2

CHF

-*CF

+ HF

. 1800 9,3

GHsNC CH

37,9

504 4,6 12

-> 2NF

19,8 400

7,5 12

-* NOa

-4-

20,9

300

11,8

-> C

+ H

40,0

791

11,8

ципло- СзНб-* GH3CHCH2

65,0

765

13-14 21

дежные значения

фф

теоретическим путем при обработке эксперименталь-

ных данных обычно рассматривают 5

фф как эмпирический параметр

(^эксп)• В табл. 11 полученные таким путем значения $

ЭК

сп сопоставлены

с числами s. (О сопоставлении $

ксп с $

фф см. в работе [1614].)

Влияние примесей

Примеси могут быть двух сортов: активные примеси, вступающие в хи-

мическое взаимодействие с исходными веществами или с продуктами их

превращения, и примени

пассивные.

Рассмотрим сначала пассивные приме-

си, действие которых прежде всего должно сказаться на процессах актива-

ции и дезактивации. На основании простой схемы Линдемана (где X —

примесь)

М + М^М*+М (Л

, /с'

М + Х^=М*+Х (k

М* —>

продукты (к*)

для эффективной константы скорости мономолекулярной реакции получим

выражение (при стационарной концентрации активных молекул М*)

»-г >'»'+> W ,.

(20

[М]

[X]

А:*

которое можно также переписать в виде:

——— г-

(20.8)

где к^ = к* {к

/к

) = /с* (&

/&х)-

В отсутствие примеси уравнение для скорости реакции можно записать

в виде:

1 d [М]

оо [М]

~ [М] dt - [М] + [М]

1/2

где [M]i/

= к^/км — концентрация М, при которой эффективная констан-

та скорости равна половине кИнтегрируя это уравнение, будем иметь

[М]

1/2

со*50% -

1П 2

+ [М]

Здесь [М]о — начальная концентрация и t

— время 50%-го превраще-

ния молекул М. Из этой формулы следует, что при малых концентра-

циях LM]о зависимость &оо£

о% от [М]

представляется гиперболой, а при

lM]

^>[M]i/

произведение &оо£

о% становится равным In 2.

Допустим теперь, что вещество М разбавлено примесью X, концентра-

ция которой удовлетворяет условию &

[Х] к*,

к'

[М]. В этом случае

скорость реакции выразится уравнением

1 d [М] k*k

~ [М] dt ^ к

интегрирование которого дает

/о

= In 2.

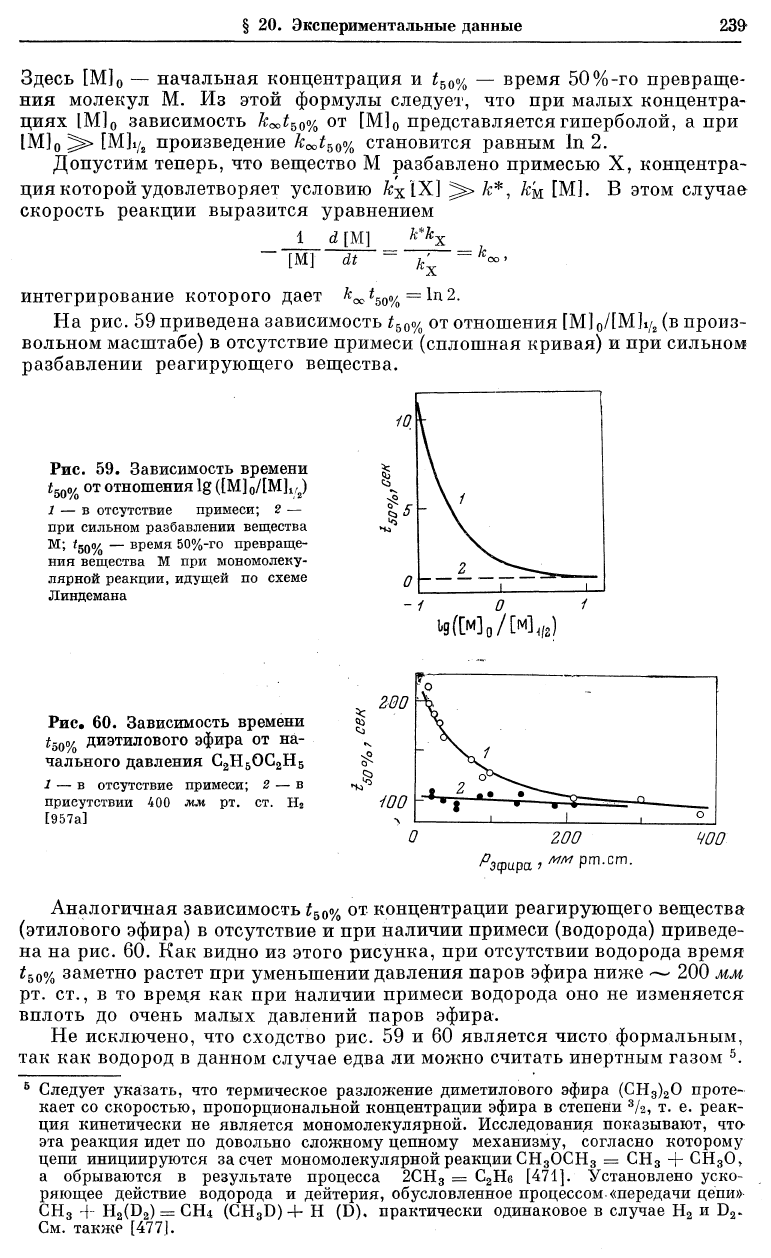
На рис. 59 приведена зависимость

b00/о

от отношения [M]

/[M]i/

(в произ-

вольном масштабе) в отсутствие примеси (сплошная кривая) и при сильном

разбавлении реагирующего вещества.

Рис. 59. Зависимость времени

*5о%

от

отношения lg ([М]

/[М]

1/2

)

1 — в отсутствие примеси; 2 —

при сильном разбавлении вещества

М; t

Q<y

— время 50%-го превраще-

ния вещества М при мономолеку-

лярной реакции, идущей по схеме

Линдемана

- / 0 1

Ц(М

/!ХУ

Рис. 60. Зависимость времени

О/ диэтилового эфира от на-

чального давления С

ОС

1 — в отсутствие примеси; 2 — в

присутствии 400 мм рт. ст. Н

[957а]

Аналогичная зависимость t

о/

от концентрации реагирующего вещества

(этилового эфира) в отсутствие и при наличии примеси (водорода) приведе-

на на рис. 60. Как видно из этого рисунка, при отсутствии водорода время

заметно растет при уменьшении давления паров эфира ниже — 200 мм

рт. ст., в то время как при наличии примеси водорода оно не изменяется

вплоть до очень малых давлений паров эфира.

Не исключено, что сходство рис. 59 и 60 является чисто формальным,

так как водород в данном случае едва ли можно считать инертным газом

Следует указать, что термическое разложение диметилового эфира (СН

)

0 проте-

кает со скоростью, пропорциональной концентрации эфира в степени

/2, т. е. реак-

ция кинетически не является мономолекулярной. Исследования показывают, чта

эта реакция идет по довольно сложному цепному механизму, согласно которому

цепи инициируются за счет мономолекулярной реакции СН

ОСН

= СН

+ СН

а обрываются в результате процесса 2СН

= С

Нб [471]. Установлено уско-

ряющее действие водорода и дейтерия, обусловленное процессом «передачи цепи»

СН

+ H

) = СЩ (CH

D)4- Н (D), практически одинаковое в случае Н

и D

См. также [477].

Эффективность активирующего и дезактивирующего действия различ-

ных газов может быть оценена количественно. Если при некоторой кон-

центрации взятого в чистом виде вещества, претерпевающего мономолеку-

лярное превращение, удельная скорость реакции равна величине

^ОО [М]

— •

[М]

+ [M]i/

•

то, увеличивая концентрацию этого вещества на Д [М], получим:

[М]

к + Ак = к

[М]

А [М]

+[М]

Такое же увеличение удельной скорости можно получить, примешивая по-

сторонний газ при соответствующей концентрации, определяемой усло-

вием

[М] + к

/к

[X]

rt I Л к* —— If ———————————————•» •

°°[М] +

[М]

1/2

+ й

[Х]

Из двух последних формул найдем:

(20

м t

l Рх

Обращаясь к химически активным примесям, заметим, что действие этих

примесей, естественно, не укладывается в рамки теории собственно моно-

молекулярных реакций и в каждом конкретном случае должно рассмат-

риваться особо.

Примеси, непосредственно взаимодействующие с исходным веществом,

обусловливают наложение на мономолекулярный процесс бимолекуляр-

ного взаимодействия этого вещества с молекулами или атомами примеси,

что приводит к искажению кинетического закона реакции. Примеси, взаи-

модействующие с продуктами распада исходного вещества, вообще говоря,

также могут изменить кинетический закон реакции, однако, лишь в тех

случаях, когда первичный процесс распада исходного вещества перестает

быть лимитирующим процессом. Чаще всего этот процесс остается лимити-

рующим и в присутствии примесей.

Ярким примером определяющего кинетику реакций влияния активных

примесей может служить реакция термического распада закиси азота

0 в присутствии иода и брома.

Согласно измерениям Фольмера PI Богдана [1645], в присутствии этих

веществ реакция идет по уравнению

ЙПЪОГ

- dt -MN2O] [Х

]Ч

где [Х

] — концентрация галогена, причем скорость реакции в среднем

в 250 раз больше скорости разложения чистой N

0. Интересно отметить,

что галоген в этой реакции не расходуется и действие его, таким

образом, нужно рассматривать как чисто каталитическое. Продуктами

каталитической реакции, как и реакции распада чистой N

0, являются

и 0

Активные примеси могут возникать также в ходе самой мономолеку-

лярной реакции. В качестве примера можно привести рассмотренный выше

распад дииодэтана, скорость которого определяется как скоростью

первичного мономолекулярного распада молекулы C

по схеме