Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

В теории молекулярных колебаний показывается [65], что v^ заключено

между наибольшей и наименьшей частотами колебаний реагирующей мо-

лекулы. Таким образом, для оценки предэкспонента получаем А ~ 10

—

сек'

. При низких температурах (кГ heof) величина А мень-

ше приведенного значения.

Однако общая трактовка, учитывающая ангармоничность колебаний^

не ограничивает сверху величину предэкспоненциального фактора, кото-

рая может превышать характерную величину 10

сек~

Ангармоничность приводит к разрыхлению внутримолекулярных связей

и образованию слабо связанной активированной молекулы. Часто об этом

эффекте говорят как о большом энтропийном вкладе [1535, 1536] активи-

рованной молекулы в сумму состояний F^, поскольку предэкспонент А

может быть выражен через изменение энтропии молекулы при переходе

ее в активированное состояние.

Наиболее простое и с количественной точки зрения наиболее важное

следствие ангармоничности при диссоциации проявляется в превращении

некоторых типов колебаний активной молекулы в свободное вращение

активированной молекулы.

Оценим по порядку величины вклад, который вносит превращение од-

ной колебательной степени свободы молекулы АВ во вращательную сте-

пень свободы активированной молекулы. При кТ Ню имеем:

~ кГ/Ясо, F

= (2jtIkT)4

(2nh). (11.21)

Выражая частоту со через параметры потенциала Морзе, получим F

^ (/Э/кТУД? где D — энергия химической связи.

В качестве примера, для которого частотный фактор оказывается ано-

мально большим, укажем на термический распад этана на два радикала

СН

. Расчет, выполненный Лином и Лейдлером [1154], моделирует моле-

кулу С

в активированном состоянии системой 17 осцилляторов (некото-

рые из которых обладают частотами, заметно меньшими соответствующих

частот молекулы) и одного ротатора (свободное внутреннее вращение груп-

пы СН

вокруг связи С—С). Координатой реакции является расстояние

С—С. Расчет дает для предэкспоненциального фактора величину 3

•

сек'

при 873° К. Эта величина согласуется с опытным значением (см. [1154]).

Перейдем теперь к бимолекулярным реакциям между частицами X

и Y. Положим вначале, что реакция протекает с преодолением активацион-

ного барьера и что активированный комплекс XY^ имеет s^ колебатель-

ных и г^ вращательных степеней свободы. Пусть далее молекулы X и Y

вместе имеют г вращательных и s колебательных степеней свободы. Для

простоты положим, что все колебательные суммы состояний исходных мо-

лекул и активированного комплекса одного порядка величины F^ ^ f

и вращательные суммы состояний F

тоя^е приблизительно равны и выра-

жаются в виде /Г (т = 1, 2 и 3 для одномерного, двумерного и трехмер-

ного^ ротатора). Тогда для предэкспонента А можно приблизительно запи-

сать:

Между величинами г, s и r^, s^ имеется соотношение, которое следует из

сохранения полного числа степеней свободы:

6 + г +

= 4 + r^ + S*. (11.23)

Число 6 в левой части выражения (11.23) относится к шести степеням сво-

боды поступательного движения сталкивающихся молекул, а число 4

в правой части (11.23) — к трем поступательным степеням свободы акти-

вированного комплекса и одной степени свободы движения по координате

реакции. Поскольку г и s заданы, при конкретизации структуры акти-

вированного комплекса остается произвол в выборе одной величины

(г^ или s^). В частности, для столкновения двух атомов или других частиц

цри пренебрежении их внутренней структурой получаем г^ = 2. Полагая,

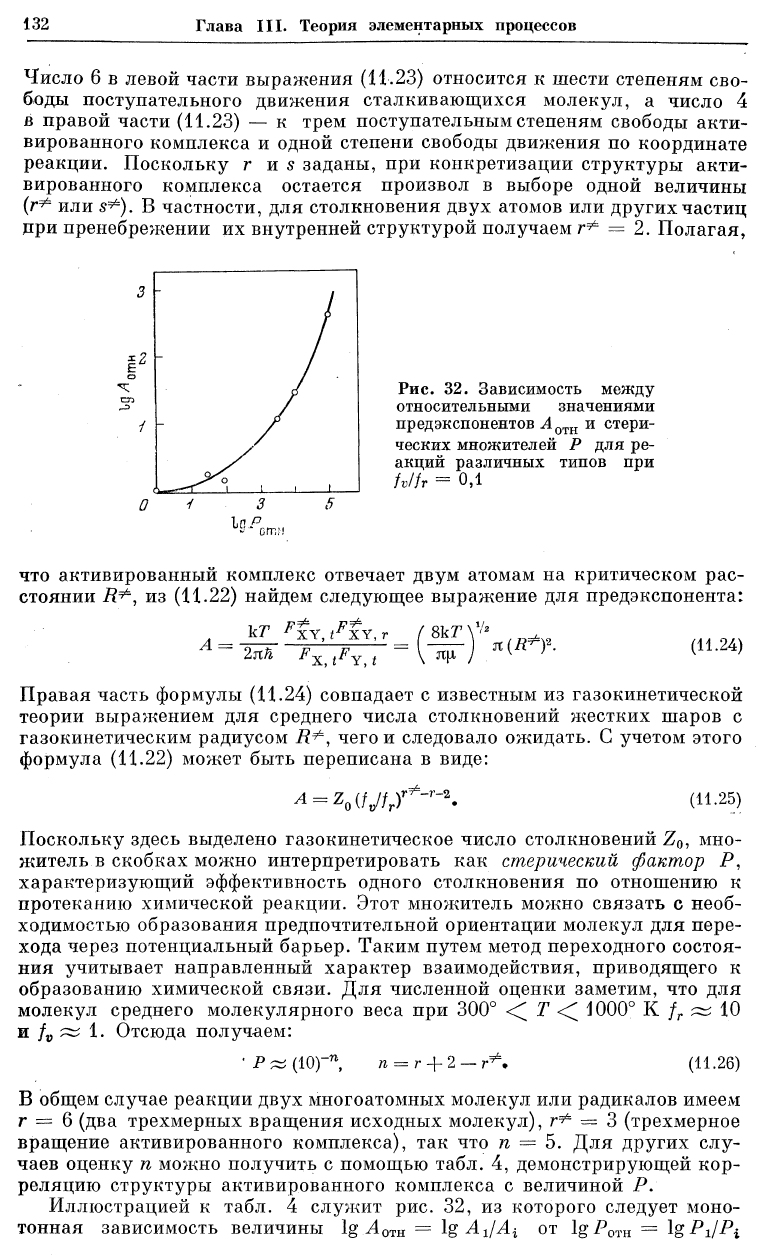
Рис. 32. Зависимость между

относительными значениями

пред экспонентов ^4

0ТН

и стери-

ческих множителей Р для ре-

акций различных типов при

hlfr = 0,1

что активированный комплекс отвечает двум атомам на критическом рас-

стоянии R^, из (11.22) найдем следующее выражение для предэкспонента:

kТ FjY, t

iy,

/8к7Л"

;; =[-щг) ("-и)

Правая часть формулы (11.24) совпадает с известным из газокинетической

теории выражением для среднего числа столкновений жестких шаров с

газокинетическим радиусом i?^, чего и следовало ожидать. С учетом этого

формула (11.22) может быть переписана в виде:

Поскольку здесь выделено газокинетическое число столкновений Z

, мно-

житель в скобках можно интерпретировать как стерический фактор Р,

характеризующий эффективность одного столкновения по отношению к

протеканию химической реакции. Этот множитель можно связать с необ-

ходимостью образования предпочтительной ориентации молекул для пере-

хода через потенциальный барьер. Таким путем метод переходного состоя-

ния учитывает направленный характер взаимодействия, приводящего к

образованию химической связи. Для численной оценки заметим, что для

молекул среднего молекулярного веса при 300° Т 1000° К /

^ 10

и f

^ 1. Отсюда получаем:

•Р^(10Г

, /г = г + 2 — г

*. (11.26)

В общем случае реакции двух многоатомных молекул или радикалов имеем

г = 6 (два трехмерных вращения исходных молекул), г^ = 3 (трехмерное

вращение активированного комплекса), так что п = 5. Для других слу-

чаев оценку п можно получить с помощью табл. 4, демонстрирующей кор-

реляцию структуры активированного комплекса с величиной Р.

Иллюстрацией к табл. 4 служит рис. 32, из которого следует моно-

тонная зависимость величины lg у4

0Т

Н = Ig-^i/Л

от lg/отн = Ig^V^i

Таблица 4

Вероятностные факторы для некоторых типов реагирующих

частиц [71, стр. 29]

Тип реагирующих частиц

Два атома

II.

Атом и двухатомная молекула

нелинейный комплекс

fvifr

линейный комплекс

(fvlfrf

III. Атом и многоатомная молекула

(fvlfrf

IV.

Две двухатомные молекулы (или двухатомная молекула

и двухатомный радикал)

нелинейный , комплекс /

(fv/frf

линейный

комплекс

(fvlfrY

Двухатомная молекула (или радикал) и многоатомная

молекула (или радикал)

(fvifr)*

VI.

Две многоатомные молекулы (или многоатомные ра-

дикал и молекула)

(fv/fr)

(i = II, III, IV,V,VI, см. табл. 4), причем А

взято равным 10

ель

•

-МОЛЬ'

-сек"

и Р

= 1. Величины А

{

представляют средние значения

предэкспоненциалъного множителя в формуле Аррениуса для типов

реакций, указанных в табл. 4, вычисленные из наиболее достоверных

значений предэкспонентов (для 120 реакций), приведенных в справочнике

[178].

Положим теперь, что реакция протекает без преодоления барьера.

В этом случае, как указывалось выше, сечение реакции может быть отож-

дествлено с сечением захвата а

(см. § 8). Сечение захвата для межмолеку-

лярного потенциала вида U (R) ~ R"

выражается формулой (8.77).

Константа скорости может быть получена либо усреднением сечения в

соответствии с формулой (8.32), либо по методу переходного состояния при

условии, что активированный комплекс соответствует положению систе-

мы на вершине центробежного барьера. Расчеты для взаимодействия иона

с молекулой и ван-дер-ваальсова взаимодействия нейтральных частиц

приводят к следующим выражениям для констант скорости [1398, 1704]:

к =

2яе (аДх)

1/2

. ./ «, ( ciioizhh

к = Ь,Пл

НъТ)"[

11 + ь

) Г '

Здесь а — поляризуемость нейтрального партнера в ионно-молекуляр-

ной реакции, характеризующейся поляризационным потенциалом U (Д) =

= — е

а/2i?

; а

, а

— поляризуемости нейтральных партнеров, для кото-

рых дальнодействующая часть потенциала аппроксимирована выраже-

нием

(

Л)

- 2 К* 17Т77'

куда входят потенциалы ионизации h и /

партнеров. Существенно, что

в выражения (11.27) и (11-28) не входят статистические суммы внутренне-

го движения партнеров. Это связано с тем, что для предполагаемой струк-

(11.27)

(11.28)

туры активированного комплекса реакция (т. е. пересечение S^) проис-

ходит на столь больших расстояниях, что вклады внутренних движений

в F* и F считаются одинаковыми, и поэтому они выпадают из отношения

Зависимость скорости реакции

от изотопного состава реагирующих молекул

Замена одного или нескольких атомов в молекуле на их изотопы при-

водит к изменению скорости элементарной химической реакции. Хотя

потенциальная поверхность, отвечающая данной элементарной реакции,

не зависит от масс атомов, входящих в состав реагирующих молекул,

однако изменение массы одного атома может существенно изменить

динамику процесса. Для равновесных реакций можно ожидать, что

метод переходного состояния правильно описывает изменение скорости

реакции с изменением изотопного состава (изотопический эффект). В рам-

ках этого приближения легко проследить зависимость константы скорости

от масс, входящих в выражение для к либо в явном виде, либо через час-

тоты колебаний, моменты инерции и числа симметрии.

Чтобы получить формулу для отношения скоростей двух реакций типа

X + Y Z, различающихся только изотопным составом одной из моле-

кул, например X, воспользуемся уравнением (И.11). При этом находим:

4-.EL

/о

X,z

~ Ft

^ (И.29)

где индексы 1 и 2 относятся к реакциям, в которых участвуют'соответст-

венно «легкие» и «тяжелые» молекулы X; EF и E

— суммы нулевых энер-

гий по всем колебательным степеням свободы активированного комплекса

и молекулы соответственно; высота барьера Е

, согласно сказанному, не

зависит от массы изотопов и поэтому из выражения (11.29) выпадает.

Обозначая через N общее число атомов, входящих в состав реаги-

рующих молекул N = N

+ Ny, ДЛЯ отношения статистических сумм

найдем:

3/V—7

П [l-expt-fcB^/kD]

FT IF? = LL

1 1 1

> 2!=1 , (11.30)

П [1

—

ехр (— Л(о'^

1кТ)]

П=1

3 V—6

F (ЛЯГ

[1-ехр (-to /кГ)]

' д [1

—

ехр (— На)

п2

/кТ)]

п=1

Здесь числа симметрии сг включают также статистический вес основного

состояния ядер*. Величины М

и М'^ представляют собой молекулярные

веса молекулы X и активированного комплекса, а А, В, С — главные

моменты инерции.

Воспользуемся теоремой Редлиха и Теллера (см. [63, стр. 250]), соглас-

но которой отношение

(ABC)

(11.32)

не зависит от масс. В выражении (11.32) Tlv

и П^ представляют

' к

<юбой соответственно произведение всех частот нормальных колебаний и

произведение всех масс атомов рассматриваемой системы в степени

В случае активированного комплекса в качестве «частоты», отвечающей

движению по координате реакции, следует подставить = со^/2я [см.

выражение (11.20)].

Пользуясь (11.32), выражение (11.30) можно переписать в следующем

виде: .

*t __ <

п/\Лп / ^М \

л,

< ТГ 1

/кГ

)

(1133)

t < nil \

n,J tl, ^ 2 / cf ii

- ехр (-

/kT) '

Аналогичное равенство можно написать для Fx, i/Fx, 2- Подставляя все

эти выражения в (11.29) и вводя обозначения Йоо

/кТ = и

, Аи

= h (со

,!— о)

)/кТ, после простых преобразований на основании (11.33)

найдем:

. , ,, ЗЛ^—6

JL = fbi ^.fj^V П /Аич 1-ехр(-

Ия

-Д

Ип

« °Х,2 of

(if / t "„ +

",г V

1 —

ехр

(—

)

•ЗЛ'—7 =6 , . =4, , . =4 > , ,

еХ

Р (- "п -

где — эффективная масса системы, движущейся по направлению

координаты реакции вблизи перевала.

Если Аи

мало по сравнению с и

, выражение (11.34) можно разло-

жить в ряд по Аи

и AUn [175, стр. 174]. Однако в наиболее интересном

случае молекул, содержащих водород, разница колебательных энергий

Аи

настолько велика, что получающаяся при этом формула неприменима,

и следует пользоваться выражением (11.34). Трудность практического

применения последнего заключается в сложности расчета эффективной

массы частот колебаний активированного комплекса. Для некоторых

реакций с участием трех атомов типа А + ВС АВ + С Бигельейзен

и Вольфсберг [493] вычислили возможные значения \itl\*>t,

что

позво-

лило при помощи сопоставления с измеренными значениями к

/к

прийти

к некоторым заключениям относительно структуры активированных

комплексов в рассматриваемых реакциях (см. также работы [1026, 1358]).

§ 12. НЕРАВНОВЕСНЫЕ ЭФФЕКТЫ В ХИМИЧЕСКИХ РЕАКЦИЯХ

При теоретическом рассмотрении химических реакций часто предпо-

лагается, что реагирующие молекулы могут быть охарактеризованы

равновесной максвелл-больцмановской функцией распределения по ско-

ростям и внутренним состояниям, хотя уже со времени формулировки

•основных понятий об элементарных процессах сознавали, что реакция

вызывает нарушение равновесного распределения. Это нарушение связа-

но с тем, что реакционноспособными оказываются только те молекулы,

энергия которых превышает некоторую предельную величину, так что

функция распределения непрерывно обедняется в высокоэнергетической

части за счет исчезновения прореагировавших молекул. Это обеднение в

какой-то степени восстанавливается в результате молекулярных столкно-

вений, и нарушение равновесного распределения будет малым только в том

•случае, если скорость восстановления равновёсного распределения на-

много превышает скорость его нарушения за счет химической реакции.

Впервые явное указание на существование значительных неравновес-

ных эффектов было получено при исследовании мономолекулярных реак-

ций в области низких давлений, где переход от реакции первого порядка

,ко второму является следствием нарушения равновесного распределения

реагирующих молекул по состояниям в области энергий, близких к энер-

гии активации.

Осознаниё этого факта вызвало появление теоретических работ по

выявлению возможных неравновесных эффектов в бимолекулярных реак-

циях. Однако исследование простых моделей показало, что неравновесные

эффекты сравнительно невелики, и соответствующие поправки к константе

скорости, вычисленной в предположении сохранения равновесия (равно-

весная константа скорости), составляют несколько процентов (см. [262,

§ 53]). Этот вывод в значительной степени был основан на том, что сечение

реакции считалось зависящим только от относительной поступательной

энергии сталкивающихся молекул, равновесное распределение по которой

восстанавливаетск очень быстро.

В последнее время был обнаружен ряд реакций обмена, кинетика кото-

рых отличается от закона второго порядка, ожидаемого на основании

стехиометрического уравнения реакции. По-видимому, это отличие обя-

зано тем же причинам, какие для мономолекулярных реакций приводят

к отклонению кинетики от закона первого порядка

—

сильному нарушению

равновесного распределения по внутренним состояниям реагирующих

молекул. Отсюда возникает важная теоретическая задача оценки неравно-

весных эффектов при учете зависимости сечения реакции от энергии раз-

личных степеней свободы реагирующих молекул. В настоящее время эта

задача только поставлена. Поэтому здесь мы ограничимся рассмотрением

простейших неравновесных процессов, иллюстрирующих общую ситуацию.

Кинетические уравнения,

описывающие обмен анергии при столкновениях

Рассмотрим вначале вопрос о восстановлении равновесного распределе-

ния молекул по энергиям в отсутствие химической реакции-. Основой для

вывода уравнений, определяющих кинетику изменений функций распреде-

ления, служат соотношения баланса между числом частиц, выбывающих

из заданного состояния и приходящих в это состояние в результате стол-

кновений. Рассмотрим для определенности обмен энергией между молеку-

лами А и В двухкомпонентной газовой смеси. Пусть а

{

и bj обозначают за-

селенности квантовых состояний i и / молекул А и В, нормированные к

полному числу молекул [А] и [В] в единице объема,

2*i= [А], [В]. (12.1)

г j

Здесь в задание квантовых состоянии / входит совокупность квантовых

чисел внутренних состояний молекул, а также величины и направления

их скоростей. Пусть далее k

(и соответственно kf£i

и kf^im)

обозначает константу скорости элементарного процесса перехода из на-

чального состояния ij в конечное состояние 1т при столкновениях моле-

кул А и В. Тогда скорость изменения заселенности а* определяется разно-

стью скоростей заселения и разрушения этого состояния в результате

столкновений:

j,Lm

<j Um

l,m, j ,

m,j

Первые два слагаемых справа учитывают переходы из состояний ij при

столкновении молекул А между собой и с молекулами В для всех возмож-

ных начальных состояний партнера по столкновению (сумма по/) во все

конечные состояния обеих сталкивающихся молекул (сумма по I и т).

Два последних слагаемых (12.2) учитывают заселение состояния i из всех

возможных состояний сталкивающихся пар А и В.

Константы kf^

и kff^

| выражаются через сечения q

молекулярных столкновений:

*tf®m = K-Ujl^m (12-3>

(щ и Uj — скорости молекул в состояниях i и ]) и удовлетворяют соотно-

шению, которое следует из детального равновесия для сечений прямых

и обратных переходов (8.38) при условии сохранения полной энергии

сталкивающейся пары

. + = + (12.4)

Уравнение, аналогичное (12.2), справедливо и для заселенности моле-

кул Ъу '

Стационарным решением уравнения (12.2) являются равновесные функ-

ции распределения

• ехр(-£

/кГ) ,ехр(-Я®/кГ)

= у [А],

= ^ [В] (12.5),

А В

Любые другие функции не обращают ^в нуль правую часть уравнений

(12.2). Будучи заданными в качестве начальных функций распределения,

они с течением времени будут приближаться к равновесным функциям

распределения. Этот процесс называется процессом тепловой релаксации.

Решение уравнений (12.2) в общем виде представляет большие мате-

матические трудности, поскольку фактически они являются системой

нелинейных интегральных уравнений

. Однако можно получить значи-

тельное упрощение общей задачи, если воспользоваться существованием

большого различия скоростей приближения функций распределения по

различным степеням свободы к соответствующим равновесным функциям.

В этом случае при рассмотрении релаксационного процесса в некото-

ром интервале времени t

— обычно удается разбить все степени свобо-

ды молекул А и В на три группы, или подсистемы: группу, для которой

процесс релаксации к моменту времени t

можно считать практически

закончившимся (равновесная подсистема); группу, для которой релакса-

ция к моменту t

еще практически не началась («замороженная» подсис-

тема), и группу, для которой функция распределения существенно ме-

няется в рассматриваемом интервале времени (релаксирующая подсисте-

ма). При этом кинетические уравнения существенно упрощаются, посколь-

ку в качестве существенных переменных в эти уравнения входят только

квантовые числа юелаксирующей подсистемы. Что касается квантовых

чисел первой и второй групп, то распределение по ним описывается из-

вестными соответственно равновесной и начальной неравновесной функ-

циями распределения.

Дальнейшее упрощение кинетических уравнений возможно, когда ре-

лаксация рассматриваемой системы в основном связана с взаимодей-

ствием с другой системой, характеризующейся равновесной функцией

распределения. Примером такой релаксации, называемой релаксацией в*

Интегральные уравнения возникают при замене суммирования по скоростям интегри-

рованием.

тепловом резервуаре, может служить релаксация газа (молекулы А),

составляющего небольшую примесь в. равновесном газе (молекулы В) с

температурой Г. При этих условиях в уравнениях (12.2) можно прене-

бречь членами, квадратичными по концентрации А, а в качестве функции

распределения Bj подставить равновесную функцию распределения Щ.

Тогда нелинейные уравнения (12.2) сводятся к линейным для заселенно-

<угей а;,

-JT- - 2 ь

(Т) а, [В] + 2 к

(Т) а

[В], (12.6)

I г

тде/^z (Т) — средние константы скорости, выражаемые через соот-

ношением:

= (12.7)

Константы скорости прямых и обратных процессов k

и кц связаны

соотношением детального равновесий:

/к

= ехр [- {Ef - Е*)!кТ], (12.8)

где Т — температура теплового резервуара.

Во многих случаях описание релаксации в терминах заселенностей

различных квантовых состояний является излишне детальным, и можно

ограничиться функцией распределения по энергиям а (Е) dE — вероят-

ности обнаружить систему релаксирующих молекул А в любых состоя-

ниях, энергия которых близка к Е и заключена в интервалр dE

Уравнение для а(Е), вытекающее из (12.2), имеет вид:

= — [В] ^ к (Е, Е') а (Е) dE' + [В] ^ к (Е', Е) a (E

) dE', (12.9)

где к (Е, Е') — вероятность перехода в единицу времени при единичных

концентрациях А и В (константа скорости) молекулы А с уровня энергии

Е на уровни в интервале энергий + dE' при единичной концентра-

ции молекул В. Вероятности переходов к(Е,Е') и к (E

, Е) удовлетво-

ряют соотношению:

к (Е, Е

) р (/?') Г E'

—

к(Е',Е)=-HW^l k Т J' <

где р (Е) — плотность энергетических уровней релаксирующих степеней

свободы молекулы А. Это соотношение является обобщением формулы

(12.8) на непрерывный спектр энергий.

В качестве характерных времен, определяющих скорость релаксации

неравновесной функции распределения (так называемые времена релакса-

ции), обычно выбирают времена, в течение которых какие-либо макроско-

пические величины, например значения энергий различных степеней сво-

боды, выражающиеся через неравновесную функцию распределения, ме-

няются в заданное число раз. Следует, однако, заметить, что такая харак-

теристика процесса релаксации не является точной, поскольку заселен-

ности различных состояний изменяются с различными скоростями. Тем

не^ менее, введение времен релаксации средней энергии различных степе-

ней свободы оказывается полезным для классификации релаксационных

процессов.

Здесь для простоты мы полагаем, что энергия Е релаксирующих степеней

свободы

может меняться непрерывно. В тех случаях, когда это условие не выполняется, ин-

тегрирование по £ в (12.9) и последующих формулах должно быть заменено суммиро-

ванием. Однако принципиальные выводы при этом не меняются.

Простейшая оценка времени релаксации через динамические характе-

ристики взаимодействия релаксирующей системы с тепловым резервуа-

ром может быть получена для случая, когда переходы в основном проис-

ходят между уровнями, разделенными энергетическим интервалом, мень-

шим кГ. В этом случае интегральное уравнение (12.9) сводится к диффе-

ренциальному уравнению в частных производных, которое вместо вероят-

ностей переходов к (Е, Е') содержит средний квадрат изменения энергии

релаксирующей системы в единицу времени (см. [262, § 35]). Эту величину,

являющуюся важнейшей характеристикой релаксационного процесса,

можно представить как произведение газокинетического числа столкно-

вений [В] Z

молекулы А с молекулами резервуара и среднего квадрата

энергии <(ДЕ)

}, переданной релаксирующей системе при одном столкно-

вении молекул А и В. Величина <(ДZ?)

> зависит от температуры теплового

резервуара и энергии Е релаксирующей системы до столкновения. В ука-

занных обозначениях релаксационное уравнение для а (Е) имеет вид:

да д Г<(АЕ)Ъ Г д I а \ а 11

ш pir-

р <*>

№[-] + • (12.11)

Это уравнение аналогично диффузионному уравнению, роль коэффи-

циента диффузии в котором играет величина [В]Z

((АЕ)

>; поэтому часто

приближение, в рамках которого (12.9) сводится к (12.11), называется

диффузионным. Упомянутое выше условие применимости диффузионного

приближения выражается неравенством:

<(Д£)2> (кГ)

. (12.12)

Рассмотрим с помощью уравнения (12.11) изменение во времени

средней энергии Ё релаксирующей системы. Величина Ё выражается

через неравновесную функцию распределения а (Е, t) соотношением

оо

#(*) = § Еа(Е, t) dE. (12.13)

Скорость Изменения средней энергии получается из (12.11) путем умно-

жения обеих частей на Е и интегрированием по всему интервалу энергии.

Таким путем получаем:

(

_ °°

dE Zn [' д I а \ а \

В общем случае интеграл в правой части не может быть выражен через

среднюю энергию Ё. Это значит, что, вообще говоря, нельзя получить

уравнения, содержащего только Ё, т. е. замкнутого уравнения, для релак-

сации средней энергии. Однако если предположить, что неравновесная

функция распределения имеет вид больцмановского распределения с не-

которой переменной температурой Т' и что отклонение Т' от Т невелико

то для Ё (t) получается уравнение:

dE Z<) <(АЕ)Ъ° -

где Е°, <(ДЕ)

)

и С = dE°IdT — энергия, средний квадрат переданной

энергии и теплоемкость (в расчете на одну молекулу) системы, находящейся

в равновесии с тепловым резервуаром. Уравнение (12.15) описывает экспо-

Это условие означает, что разность температур Т' — Т можно считать пропорцио-

нальной отклонению мгновенной средней энергии от равновесного значения Е — Е°.

ненциальное приближение энергии Е к равновесному значению с харак-

теристическим временем релаксации т,

1 Z, <(A£)

>° ' ,

— - — I

] "таг- (

Это время выражается через такие параметры релаксирующей системы,,

которые характеризуют ее взаимодействие с тепловым резервуаром в со-

стоянии равновесия. Последнее обстоятельство позволяет сравнительно'

легко получать оценки т, не рассматривая в явном виде решения релак-

сационных уравнений. Следует, однако, иметь в виду, что вследствие упро-

щенного подхода к решению релаксационной задачи величина т, опреде-

ленная выражением (12.16), в общем случае может передавать лишь поря-

док величины времени, характеризующего скорость приближения нерав-

новесной функции распределения к равновесной.

Релаксация по поступательным,

вращательным и колебательным степеням свободы.

Перейдем теперь к обсуждению различных типов релаксационных ьро-

цессов, которые в известной степени можно считать независимыми.

Поступательная релаксация. Релаксация функции распределения по

скоростям, называемая поступательной релаксацией, является, вообще

говоря, наиболее быстрым из всех релаксационных процессов, если при

каждом столкновении кинетическая энергия молекул меняется на величину

порядка самой энергии. Такие условия обмена энергией выполняются

при столкновении молекул соизмеримых масс. Если начальная неравно-

весная функция распределения отличается от равновесной в области

максимума последней, то релаксация практически завершается за время

нескольких молекулярных столкновений. Если пренебречь релаксацион-

ными процессами в этот промежуток времени для других степеней свободы,

то под

а-

в уравнении (12.2) сдедует понимать функцию распределения по

скоростям, причем индекс i определяет величины и направления скоростей

молекул А. Суммирование по индексам/,

тв (12.2) в этом случае заменя-

ется интегрированием по величинам и направлением скоростей, причем

константы скорости kf^i

выражаются через дифференциальное сечение-

упругого рассеяния:

Обозначая функции распределения по скоростям молекул А и В через

/А (ив)

/В (U

)

подставляя их вместе с (12.17) в (12.2), получим систему

двух интегральных уравнений для функций распределения /А И /

Рассмотрим более подробно два предельных случая, представляющих

практический интерес: однокомпонентную систему А и двукомпонентную

систему А+В с малой относительной концентрацией молекул А.

В первом случае релаксация обусловлена столкновениями молекул А

между собой, и уравнение для неравновесной функции распределения

принимает вид:

^А (U) IT

~~АГ~

)) If А (*') /А (%) - /А (И) /А О*)] | U - UI

I G

(I U - Щ I, О, Ф) dQdu

(12.18)

где и' и и/ — скорости сталкивающихся молекул после столкновения,,

которые полностью определяются скоростями молекул до столкновения

и и и

и углами рассеяния Ф и ср. Уравнение (12.18) является известным

уравнением Болъцмана, решение которого исследовано весьма подробно

для малых отклонений функции распределения от равновесной и исполь-