Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

вдоль оси ж заканчивающейся тупиком (см. рис. 23). При достаточно

больших значениях координаты RА сечение поверхности потенциальной

энергии плоскостью, перпендикулярной R\, дает кривую потенциальной

энергии изолированной молекулы ВС.

Линейное столкновение атома А с молекулой ВС может приводить

либо к колебательному возбуждению молекулы, либо к ее диссоциации.

Если полная энергия системы Е меньше энергии диссоциации молекулы,

то возможно только возбуждение молекулы. Пусть в начальном состоя-

нии колебательная энергия молекулы равнялась нулю. Тогда сближение А

и ВС изображается на поверхности потенциальной энергии прямолинейным

участком траектории (прямая 5), проходящей к тупику по дну долины.

Процесс колебательного возбуждения соответствует отражению точки от

тупика, причем разлет атома А и возбужденной молекулы ВС описывается

синусообразной траекторией, которая не может пересечь эквипотенциаль-

ную линию I, соответствующую полной, энергии Е (см. рис. 23).

Если энергия Е превышает энергию диссоциации D, то траектория

после достижения линии 2 может выйти из долины и привести изобража-

ющую точку на плато, соответствующее диссопиированному состоя-

нию: в этой области конфигурационного пространства все три атома*на-

ходятся достаточно далеко один от другого и практически не взаимодей-

ствуют.

Следует отметить, что поверхность потенциальной энергии, отвечаю-

щая основному электронному состоянию системы, может смыкаться в области

плато с другими поверхностями, которые отвечают низшим электронно-

возбужденным состояниям. Это отражает факт вырождения электронного

состояния системы свободных атомов.

Рассмотрим теперь нелинейную конфигурацию атомов. Для выделения

' угловой зависимости взаимодействия потенциал U обычно представляют

в виде суммы симметричной V

и антисимметричной V

частей; последняя

исчезает при усреднении по углам 7. При достаточно малой асимметрии

величина V

может быть представлена в виде быстро сходящегося разло-

жения по степеням cos 7 или полиномам Лежандра Р\ (cos 7) [69]. Таким

образом, потенциальная энергия системы атом + двухатомная молекула

записывается в виде:

оо

(R,

г, Т) г) + 2

«> * (

(

C0S Т)

' (

х=1

где V

и V

,\ — функции двух переменных R и г. Если молекула состоит

из одинаковых атомов, то потенциал взаимодействия остается неизмен-

ным при замене 7 на л — 7. Поскольку при такой замене cos 7 меняет

знак, полиномы Лежандра с нечетным индексом X, являющиеся нечетными

функциями cos 7, отсутствуют в сумме (9.9), т. е. суммирование проводится

только по четным X. Первый член разложения Р

(cos 7) — (3 cos

7—1)/2

часто является единственным членом, который привлекается для описа-

ния угловой зависимости взаимодействия.

Для гантельной модели, где потенциалы V

х выражаются определен-

ным образом через &АВ, С^ВС И UAC, ДОЛЖНО ВЫПОЛНЯТЬСЯ соотношение

dVJdR

ldr (уменьшение отталкивания между А и ВС при за-

данных R, 7 = л/2 и растяжении В—С). Выполнение этого условия для

неэмпирического потенциала является критерием того, что система моя^ет

быть аппроксимирована моделью, в которой потенциал есть сумма парных

потенциалов. Таким образом, было найдено, например, что подобная мо-

дель качественно описывает взаимодействие в системе Li

+ Н

[1143],

но должна быть отвергнута для системы Не + Н

L859, 1105].

Взаимодействие атомов в трехатомной молекуле

Основная особенность поверхности потенциальной энергии системы

трех атомов, составляющих устойчивую трехатомную молекулу, заклю-

чается в наличии потенциальной ямы, минимум которой отвечает равновес-

ной конфигурации молекулы в данном электронном состоянии. Вблизи

минимума любая функция может быть представлена в виде полинома

второй степени по смещениям координат от положения равновесия (так

называемое гармоническое приближение). Например, в координатах г

АВ

?'вс и 0 (0 — угол между г

в и r

) потенциальная энергия молекулы ABC

в гармоническом приближении может быть представлена в виде:

где q

= r

— r

; q

= r

— r

; q

= 0 — 0

; Кц — силовые кон-

станты; г

АВ

, г

вс

, 8

— параметры равновесной конфигурации.

Что касается кинетической энергии, то она всегда представляется

в виде полинома второй степени по скоростям, соответствующим выбран-

ным координатам, и коэффициенты этого полинома можно считать по-

стоянными, зависящими только от значений координат в положении рав-

новесия. В этом приближении вращение молекулы можно рассматривать

независимо от колебаний, и при расчете энергии вращения молекулу можно

считать жестко фиксированной в равновесной конфигурации.

Кинетическая энергия колебаний имеет вид:

«i

Выражения (9.10) и (9.11) определяют полный колебательный гамильто-

ниан молекулы в гармоническом приближении. Исследование динамики

движения такой гармонической системы показывает, что от набора пере-

менных qi можно линейным преобразованием перейти к такому новому

набору переменных (?

, в которых полный колебательный гамильтониан

представляется в виде суммы гамильтонианов, каждый из которых зависит

только от Q\ и Q\:

Я = 2

х, -(9.12)

JJU

= — (Q

+ (9.13)

Представление.II в виде суммы означает, что переменные Q\ разделяются,

и движения по различным координатам Q\ независимы. Каждый из га-

мильтонианов Н\ представляет гамильтониан гармонического осцилля-

тора, и временная зависимость Qx дается известной формулой [63]:

Qx = (2e

/Hx<*>x)

cos

К* +

Фх

). (9.14)

Координаты Qx называются нормальными координатами многоатомной

(в рассматриваемом случае трехатомной) молекулы, частоты со

— часто-

тами нормальных колебаний; ju,x и 8х — эффективная масса и энергия

Я-го нормального колебания. В этом приближении полная энергия системы

дредставляется в виде суммы не зависящих от времени энергий 8

(9.15)

Рис. 24. Поверхность потенциальной энергии линейной молекулы С0

в состоянии

[63]

Формулы (9.14) совместно с законом преобразования от Qx к q

{

пол-

ностью определяют динамику колебаний многоатомной молекулы в гар-

моническом приближении. Это приближение справедливо, однако, до тех

пор, пока форма потенциальной поверхности мало отличается от эллип-

тического параболоида [приближение (9.10)], аппроксимирующего эту

поверхность вблизи минимума. По мере увеличения & в разложение

(9.11) следует вкл!очить высшие степени q

учитывающие ангармонич-

ность колебаний. С учетом ангармоничности поверхность потенциальной

энергии пригодна для описания процесса диссоциации молекулы. При

этом, однако, уже невозможно ввести нормальные координаты и свести

многомерное движение изображающей точки по поверхности потенциаль-

ной энергии к суперпозиции одномерных движений.

На рис. 24 показана поверхность потенциальной энергии основного

синглетного состояния молекулы С0

при линейном расположении ядер.

Равновесная конфигурация молекулы определяется точкой г

= 1,160 А.

Вблизи этой точки эквипотенциальные линии должны иметь форму эллип-

сов с главными осями, направленными по прямым аа и ЪЪ (в масштабе

рисунка не показаны). Движение точки вдоль прямых аа и

ЪЪ

соответст-

вует нормальным колебаниям С0

: симметричному валентному колебанию

(направление аа) и антисимметричному валентному колебанию (направ-

ление ЪЪ). По мере повышения энергии эквипотенциальные линии все

больше отличаются от эллипсов, причем появляется тенденция к образо-

ванию выходов из ямы. Эти выходы вдоль каждой из долин отвечают

разрыву одной из связей С—О в молекуле С0

. Сечение поверхности по-

тенциальной энергии вдоль прямой, параллельной оси r

при г

~> оо

дает терм основного состояния молекулы СО. Показанная на рис. 24

картина поверхности потенциальной энергии молекулы С0

получается

при условии выполнимости правила Вигнера о сохранении полного спина

системы; она приводит к основному электронному состоянию молекулы

СО и возбужденному состоянию атома О. Вследствие этого изображенная

на рис. 24 поверхность пересекается с поверхностью потенциальной энер-

8 В. H. Кондратьев, Е. Е. Никитин

гии триплетного состояния С0

, которое при г

оо и г

->• оо лежит

ниже. Триплетное состояние приводит к молекуле СО и атому О в основ-

ном состоянии. Линии пересечения этих двух поверхностей показаны на

рис. 24 пунктиром.

Поверхность потенциальной энергии

для реакции А -J- ВС = АВ -f- С

Поверхность потенциальной энергии для системы трех атомов, уча-

ствующих в реакции обмена, характеризуется двумя долинами, движение

изображающей точки в которых отвечает относительному движению А

и ВС или АВ и С.

Для обсуждения энергетики реакции обмена введем понятие пути

реакции как линии в конфигурационном пространстве, отвечающей ми-

нимальной энергии взаимодействия атомов и ведущей от исходных моле-

кул к конечным. Сечение поверхности потенциальной энергии вдоль пути

реакции называется профилем пути реакции. Разность потенциальных

энергий Q

ДЛЯ начального и конечного состояний характеризует изме-

нение энергии в данной реакции. В частности, теплота реакции Q опре-

деляется как суммарное изменение потенциальной энергии Q

и измене-

ние нулевой энергии колебаний

Q = Q

+ AE

. (9.16)

Здесь АЕ

обозначает разность нулевых энергий колебаний исходной и

конечной молекул AE

= E

— E'

Если реакция протекает через образование комплекса ABC, энергия

связи которого положительна по отношению к распаду на фрагменты

АВ + С и А + ВС, то поверхность потенциальной энергии такой системы

в принципе аналогична поверхности потенциальной энергии устойчивой

трехатомной молекулы ABC, способной диссоциировать по двум каналам.

Для большинства обменных реакций характерно наличие потенциаль-

ного барьера, через который проходит путь реакции.

Профили различных путей реакций показаны на рис. 25. Характерная

особенность таких реакций состоит в том, что даже при экзотермическом

направлении реакции исходные молекулы должны обладать достаточным

запасом энергии для цреодоления энергетического барьера Е

0 f

Происхождение энергетического барьера обязано перестройке элек-

тронной структуры молекулы, участвующей в реакции, которая сводится

к разрушению химической связи ВС и образованию новой связи АВ.

Приближенно такая перестройка описывается суперпозицией двух вол-

новых функций Я|)А,ВС и г|)

АВ

,с, первая из которых отвечает взаимодейст-

вию атома А с молекулой ВС, а вторая — атома С с молекулой АВ [391]:

ВС +

^АВ, С- (

9Л7

Коэффициенты а и с меняются вдоль пути реакции в соответств ии с непре

рывным переходом от начального состояния системы (А, ВС) к конечному

(АВ, С). Качественное представление об общем характере поверхности

потенциальной энергии системы, описываемой функцией (9.17), можно

получить, рассматривая сначала две независимые поверхности потен-

циальной энергии, отвечающие функциям if)

ABG

и if>

,c и учитывая затем

их взаимодействие.

Поверхность потенциальной энергии для функции I|)A,BC качественно

йй а логична поверхности, описывающей взаимодействие молекулы ВС

с инертным атомом А (см. рис. 24). Для функции

имеет место ана-

логичная картина, только долина направлена параллельно оси а не

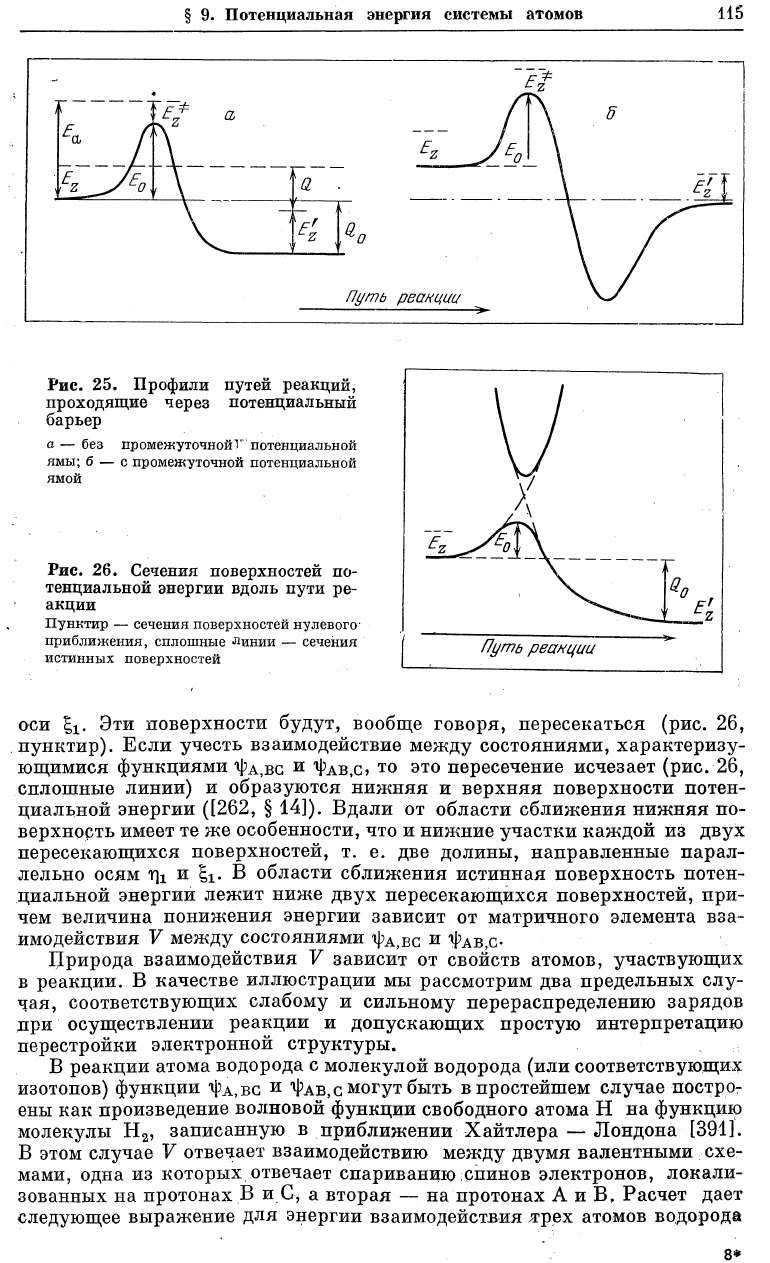
Рис. 25. Профили путей реакций,

проходящие через потенциальный

барьер

а— без промежуточной Г потенциальной

ямы; б — с промежуточной потенциальной

ямой

Рис. 26. Сечения поверхностей по-

тенциальной энергии вдоль пути ре-

акции

Пунктир — сечения поверхностей нулевого-

приближения, сплошные Линии — сечения

истинных поверхностей

оси Эти поверхности будут, вообще говоря, пересекаться (рис. 26,

пунктир). Если учесть взаимодействие между состояниями, характеризу-

ющимися функциями 'ФА,вс и я|)

АВ с

, то это пересечение исчезает (рис, 26,

сплошные линии) и образуются нижняя и верхняя поверхности потен-

циальной энергии ([262, § 14]). Вдали от области сближения нижняя по-

верхность имеет те же особенности, что и нижние участки каждой из двух

пересекающихся поверхностей, т. е. две долины, направленные парал-

лельно осям % и В области сближения истинная поверхность потен-

циальной энергии лежит ниже двух пересекающихся поверхностей, при-

чем величина понижения энергии зависит от матричного элемента вза-

имодействия V между состояниями O|?A,BC И

Природа взаимодействия V зависит от свойств атомов, участвующих

в реакции. В качестве иллюстрации мы рассмотрим два предельных слу-

чая, соответствующих слабому и сильному перераспределению зарядов

при осуществлении реакции и допускающих простую интерпретацию

перестройки электронной структуры.

В реакции атома водорода с молекулой водорода (или соответствующих

изотопов) функции ij)

,BC

'ФАВ, С могут быть в простейшем случае постро-

ены как произведение волновой функции свободного атома Н на функцию

молекулы Н

, записанную в приближении Хайтлера — Лондона [391].

В этом случае V отвечает взаимодействию между двумя валентными схе-

мами, одна из которых отвечает спариванию спинов электронов, локали-

зованных на протонах В и С, а вторая — на протонах А и В, Расчет дает

следующее выражение для энергии взаимодействия ярех атомов водорода

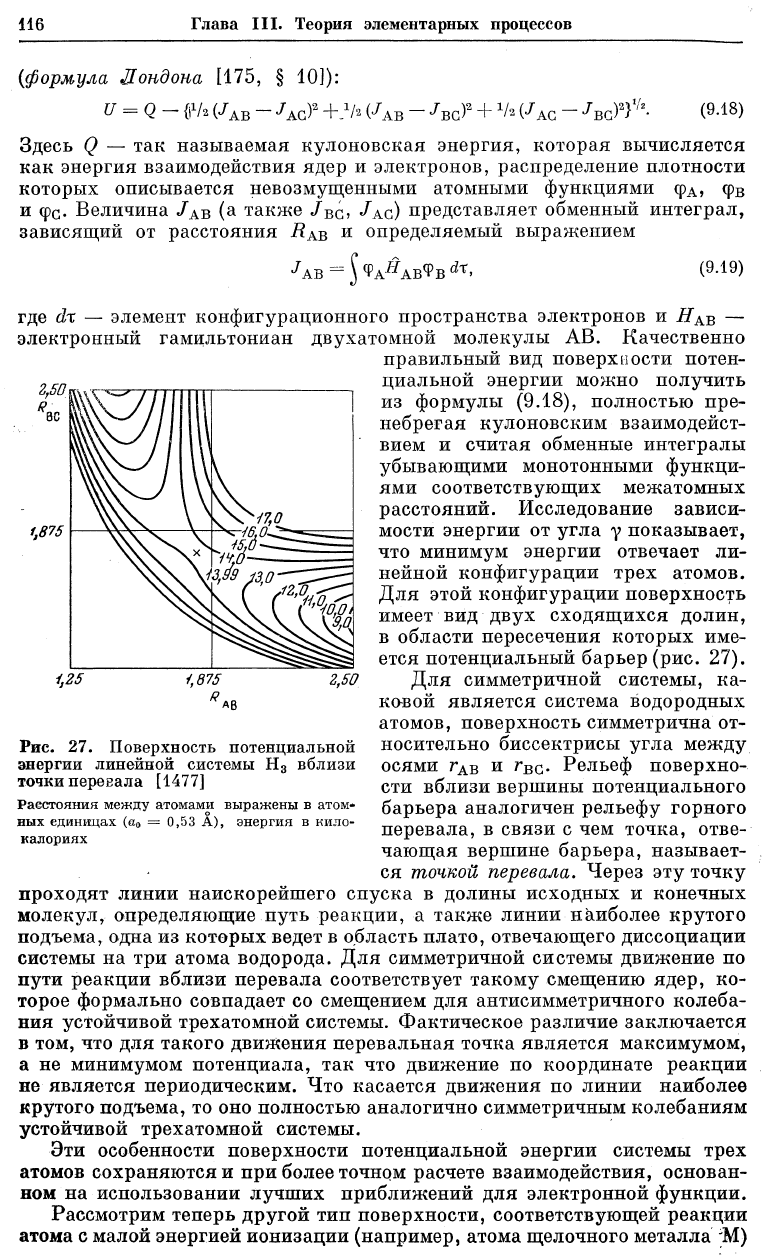
{формула Лондона [175, § 10]):

U = Q- (iV

- J

f +.V2 (/

АВ

~ V + Va (/

АС

- /

вс

)

}

1/2

- (9.18)

Здесь Q — так называемая кулоновская энергия, которая вычисляется

как энергия взаимодействия ядер и электронов, распределение плотности

которых описывается невозмущениыми атомными функциями ф

, ср

и фс. Величина /

АВ

(а также /

вс

, J АС) представляет обменный интеграл,

зависящий от расстояния i?

и определяемый выражением

где dx — элемент конфигурационного пространства электронов и if

—

электронный гамильтониан двухатомной молекулы АВ. Качественно

правильный вид поверхности потен-

циальной энергии можно получить

из формулы (9.18), полностью пре-

небрегая кулоновским взаимодейст-

вием и считая обменные интегралы

убывающими монотонными функци-

ями соответствующих межатомных

расстояний. Исследование зависи-

мости энергии от угла у показывает,

что минимум энергии отвечает ли-

нейной конфигурации трех атомов.

Для этой конфигурации поверхность

имеет вид двух сходящихся долин,

в области пересечения которых име-

ется потенциальный барьер (рис. 27).

Для симметричной системы, ка-

навой является система водородных

атомов, поверхность симметрична от-

носительно биссектрисы угла между

осями г

АВ

и г

вс

. Рельеф поверхно-

сти вблизи вершины потенциального

барьера аналогичен рельефу горного

перевала, в связи с чем точка, отве-

чающая вершине барьера, называет-

ся точкой перевала. Через эту точку

проходят линии наискорейшего спуска в долины исходных и конечных

молекул, определяющие путь реакции, а также линии наиболее крутого

подъема, одна из которых ведет в область плато, отвечающего диссоциации

системы на три атома водорода. Для симметричной системы движение по

пути реакции вблизи перевала соответствует такому смещению ядер, ко-

торое формально совпадает со смещением для антисимметричного колеба-

ния устойчивой трехатомной системы. Фактическое различие заключается

в том, что для такого движения перевальная точка является максимумом,

а не минимумом потенциала, так что движение по координате реакции

не является периодическим. Что касается движения по линии наиболее

крутого подъема, то оно полностью аналогично симметричным колебаниям

устойчивой трехатомной системы.

Эти особенности поверхности потенциальной энергии системы трех

атомов сохраняютсяи при более точном расчете взаимодействия, основан-

ном на использовании лучших приближений для электронной функции.

Рассмотрим теперь другой тип поверхности, соответствующей реакции

атома с малой энергией ионизации (например, атома щелочного металла М)

Рис. 27. Поверхность потенциальной

энергии линейной системы Н

вблизи

точки перевала [1477]

Расстояния между атомами выражены в атом-

ных единицах (а

. = 0,53 А), энергия в кило-

калориях

с молекулой, обладающей большим сродством к электрону (например,

молекула галогена Х

М + Х2

—»

•

Х~

—>

MX + X. (9.20)

Для таких реакций характерно превращение ковалентной связи исходной

молекулы в ионную связь конечной молекулы. При этих условиях в ка-

честве нулевого приближения можно рассматривать пересекающиеся по-

верхности, одна из которых отвечает взаимодействию атома М с кова-

лентной молекулой Х

(«ковалентная» поверхность), а другая — взаимо-

действию иона М

с X" — X («ионная» поверхность). Линия пересечения

этих поверхностей определяется условием компенсации разности потен-

циала ионизации атома М и сродства к электрону молекулы Х

кулонов-

ским притяжением между М

и парой X" — X. Для рассматриваемых

реакций типичные величины координаты точки пересечения оказываются

порядка 5—10 А. На столь больших расстояниях взаимодействие между

ионным и ковалентным состояниями оказывается таким малым, что при-

ближенно истинная поверхность потенциальной энергии может быть по-

строена из участков «ковалентной» и «ионной» поверхностей, линия пере-

сечения которых является линией излома адиабатической поверхности

потенциальной энергии [262].

§ 10. НЕАДИАБАТИЧЕСКИЕ ПРОЦЕССЫ

Как отмечалось в § 8, в адиабатическом приближении каждому элек-

тронному состоянию системы атомов сопоставляется поверхность потен-

циальной энергии, которая определяет движение ядер в данном электрон-

ном состоянии. Критерием применимости адиабатического приближения

служит большая величина параметра Месси, пропорционального разности

потенциальных энергий, отвечающих двум поверхностям. Качественное

исследование относительного расположения поверхностей указывает на

следующие возможности пересечения поверхностей потенциальной энер-

гии [262]. .

1. Если две поверхности потенциальной энергии системы ядер с s

степенями свободы отвечают электронным функциям различной симмет-

рии, то они могут пересекаться по (s — 1)-мерной линии

. Для системы

с одной степенью свободы (система двух атомов) это означает возможность

пересечения термов разной симметрии в одной точке; для системы с двумя

степенями свободы (система трех атомов при фиксированной одной коор-

динате) — возможность пересечения поверхностей потенциальной энер-

гии вдоль некоторой кривой.

2. Если две 5-мерные поверхности потенциальной энергии отвечают

электронным функциям одинаковой симметрии и спин-орбитальное

взаимодействие не учитывается, то эти поверхности могут пересекаться

вдоль (s — 2)-мерной линии. Для системы с одной степенью свободы это

означает невозможность пересечения термов одинаковой симметрии; для

двух степеней свободы — пересечение двумерных поверхностей в одной

точке.

3. Если две 5-мерные поверхности отвечают электронным функциям

одинаковой симметрии, то при учете спин-орбитального взаимодействия

эти поверхности пересекаются вдоль (s — 3)-мерной линии. Для одной

и дву;£ степеней свободы это означает невозможность пересечения термов.

При движении по этой линии изменяется s — 1 степень свободы.

Пересечения или резкие сближения (квазипересечения) поверхностей

приводят для некоторых траекторий к малым значениям параметра Месси,

что указывает на неприменимость адиабатического приближения, т. е.

на возможность неадиабатических переходов. Вероятности таких пере-

ходов зависят не только от параметра Месси, но и от величины матрич-

ного элемента взаимодействия, вызывающего неадиабатические переходы.

Классификация неадиабатических переходов

В полуклассическом приближении оператор неадиабатического [вза-

имодействия выражается производной —iUdjdt, действующей на элек-

тронные адиабатические функции я)^; последние зависят от времени вслед-

ствие того, что координаты ядер, входящие в электронные функции в ка-

честве параметров, меняются при движении ядер (см. § 8). Поскольку ади-

абатические функции классифицируются по различным типам симметрии

гамильтониана при фиксированных ядрах, той оператор неадиабатического

взаимодействия целесообразно представить в таком виде, который ото-

бражал бы различающиеся по симметрии типы движения ядер. Для

выяснения этого вопроса рассмотрим простейший случай системы двух

атомов.

При неподвижных ядрах гамильтониан электронов обладает осевой

симметрией и вследствие этого электронные адиабатические функции

могут быть охарактеризованы квантовыми числами й. Адиабатические

термы системы в этом случае зависят только от одного параметра —

межъядерного расстояния R. Пара адиабатических термов отвечает

функциям одной симметрии, если последние характеризуются одинако-

выми величинами проекции углового момента электронов на молеку-

лярную ось (квантовые числа £2), и функциям разной симметрии, если

последние характеризуются различными величинами й. В первом случае

возможно квазипересечение термов, во втором — пересечение.

Рассматривая движение ядер, заметим,- что любое смещение можно

представить как линейную комбинацию радиального движения, не меня-

ющего ориентацию молекулярной оси, и вращательного движения, не

меняющего расстояния между ядрами. В соответствии с этим оператор —

ihdldt может быть представлен как сумма операторов, каждый из которых

учитывает один из указанных видов движения [262]:

Здесь R и со — радиальная и угловая скорости относительного движения

ядер и — оператор проекции углового момента электронов на вектор

угловой скорости ядер. Из уравнения (10.1) следует, что матричные эле-

менты оператора — ihdfdt выражаются через матричные элементы опера-

торов d/dR и /о, которые уже не зависят от скорости движения ядер и

относительно которых известны условия их обращения в нуль. Именно

матричный элемент оператора d/dR отличен от нуля только в том случае,

если начальное и конечное расстояния отвечают одному и тому же типу

симметрии, а матричный элемент отличен от нуля только когда кванто-

вые числа Q начального и конечного состояний различаются на единицу.

Таким образом, радиальное движение атомов вызывает неадиабатические

переходы только между термами одинаковой симметрии, а вращательное

движение — между термами различной симметрии с величинами проекций

углового момента электронов на ось, соединяющую ядра, различающимися

на ±1,

Кроме осевой симметрии система двух атомов может обладать другими

элементами симметрии, относительно которых также формулируются

правила отбора для оператора неадиабатической связи [261, 263]. Эти

правила аналогичны правилам отбора для предиссоциации

(

двухатомных

молекул [64, 207].

Для системы трех и большего числа атомов оператор неадиабатической

связи также может быть представлен как линейная комбинация операто-

ров, каждый из которых отвечает определенному характеру движения

атомов. Правила отбора для системы трех атомов обсуждаются в обзоре

1261].

Указанная выше классификация возможных типов неадиабатических

переходов существенно облегчает анализ общей картины взаимодействия

движений электронов и ядер, позволяя упростить систему уравнений

(8.53). Критерий Месси (£ ^1) устанавливает положение областей не-

адиабатичности в конфигурационном пространстве ядер. При достаточно

малых скоростях ядер размеры этих областей велики, и это позволяет

аппроксимировать адиабатические термы и матричные элементы неадиа-

батического взаимодействия в этих областях простыми функциями, для

которых уравнения неадиабатического взаимодействия позволяют найти

сравнительно простые решения и, таким образом, вычислить вероятности

неадиабатических переходов.

Вероятности неадиабатических переходов

В настоящее время известен ряд моделей взаимодействия, для которых

вероятность перехода получена в общем виде [263, 1291, 1292]. Мы огра-

ничимся рассмотрением двух таких моделей, относящихся к случаям пе-

ресечения и квазипересечения термов. Для простоты будем иметь в виду

столкновение двух!атомов, хотя многие из полученных при этом резуль-

татов могут быть перенесены и на более сложные системы.

Если два адиабатических терма U

и £7

пересекаются, то они отвечают

функциям разной аксиальной симметрии. Неадиабатическая связь между

этими термами осуществляется вблизи точки пересечения, где параметр

Месси обращается в нуль. В этой области матричный элемент неадиабати-

ческой связи Ci,2, равный со (/co)i,2

отличный от нуля при рассмотренных

выше правилах отбора, можно считать постоянным, а термы можно

аппроксимировать линейными функциями Д. Таким образом, мы приходим

к следующей формулировке модели, рассмотренной впервые Ландау

11128]:

—

(Л

—

)

= -F

(R-R

) + E

. (Ю.2)

i;2

®(/Ji

Здесь Н

—координата точки пересечения термов: —

^ аа

дД

и Е

— величина энергии в точке пересечения

.R=jRo

термов. Аппроксимируем далее участок траектории вблизи точки пере-

сечения линейной функцией времени, полагая

R — R

= ht, * г (Ю.З)

где R — радиальная скорость относительного движения атомов. Тогда

в» первом порядке теории возмущений получаем следующее выражение

для вероятности Р

неадиабатического перехода:

1,2 '

1 f Г i f li

2ясо

(,-jf

(10.4)

Величины со и R являются функциями прицельного параметра Ъ и ско-

рости атомов до столкновения и. Эти функции находятся из закона сохра-

нения углового момента относительного движения и закона сохранения

энергии:

(10.5)

•

-"о

R = u{ 1

Л &

2?„VV.

(10.6)

где Е — кинетическая энергия атомов; Е = \хи

/2. Выражение (10.4)

для вероятности перехода справедливо при условии Р

1?2

U(R)

/ч

Рис. 28. Пересечение адиаба-

• ^—

тических термов

1—1 — адиабатический путь про-

цесса; 1—2 — неадиабатический

^ 1

путь

Оценки показывают [263], что это условие всегда выподняется, если

в области взаимодействия справедлива аппроксимация (10.2). Таким

образом, в этом случае система атомов с-вероятностью — 1 — Р

1У2

следует по поверхности потенциальной энергии, соответствующей на-

чальному адиабатическому терму (рис. 28).

Подстановка выражения (10.5) в (10.4) позволяет выразить вероят-

ность неадиабатического перехода через прицельный параметр, вычислить

сечение и затем константу скорости неадиабатического процесса. При

этом нужно учесть, что при атомных столкновениях точка пересечения

проходится дважды: первый раз при сближении атомов, второй раз —

при разлете. Поэтому при вычислении сечения в качестве вероятности

перехода должна быть использована величина означающая вероят-

ность двойного прохождения системой области пересечения термов. Ве-

личина #>1,2 выражается через Р

1>2

соотношением:

В рассматриваемом случае JP

1>2

1 и ^1,2 = 2

Расчет дает следующее выражение для константы скорости неадиаба-

тического процесса:

где

( SkT Vh .

\~щГ)

Я/?

0 <*1,2>

еХ

Р ("

/«(2k 77^(/J

ls2

^ol^i-

(10.8)

(10.9)

средняя вероятность перехода.