Кочарян Г.Г. Деформационные процессы в массивах горных пород

Подождите немного. Документ загружается.

341

Таблица 9.2 Характеристики параметров излучателя

при взрыве в прочной породе.

Q, кг a

м b

, м T

, мсек

0,001 0.01 0.07 0.1

0.1 0.05 0.3 0.5

1.0 0.1 0.7 1.1

9.0 0.2 1.5 2.3

На рис.9.6 приведены результаты измерений параметров

сейсмических волн при небольших взрывах в скальной породе.

Относительно частотного состава колебаний уместно сделать

следующее замечание. Как видно из результатов измерений (рис.9.6)

на больших расстояниях период сигнала практически не зависит от

веса заряда, а определяется, главным образом, диссипативными

характеристиками среды. Это соответствует представлениям

линейной

теории поглощения, согласно которой на больших

расстояниях форма сейсмического импульса определяется лишь

видом функции поглощения. Подчеркнем, что для малых зарядов

наблюдаемые периоды могут быть заметно выше расчетных,

поскольку здесь существенными оказываются эффекты поглощения

высоких частот при прохождении волн через системы трещин

неизменно присутствующих в горном массиве.

9.2 Физическое моделирование взрывов

Физическое моделирование является эффективным методом

изучения взрывных процессов. Однако, такое сложное явление как

подземный взрыв, не удается воспроизвести на одной какой-либо

модели, что обусловлено многообразием протекающих физических

процессов и различием сменяющих друг друга фаз развития.

Раздел написан к.т.н. Л.М.Перником

342

Поэтому для исследования подземного взрыва применяют

различные математические и физические модели, нацеленные на

изучение какой-либо определенной стадии развития взрыва,

стремясь при этом максимально возможно упростить модель за счет

пренебрежения второстепенными эффектами.

Так, например, при моделировании сейсмического действия

взрыва, во многих случаях можно существенно упростить неупругие

стадии деформирования среды рассматривая сейсмический

источник

в виде центра расширения в квазиупругой среде. При проведении

физических экспериментов, в этом случае следует в первую очередь

заботиться о соответствии прочностных и диссипативных констант

модельной и природной среды, поскольку пересчет параметров при

взрывах разного масштаба в средах с близкими характеристиками

легко осуществляется на основе геометрического подобия (см. (9.1)

и (9.13)-(9.16)).

Моделирование дробящего или экскавационного действия

взрыва оказывается более сложным, требует введения

дополнительных предположений и контроля параметров модели в

соответствии с теорией подобия.

Рассмотрим основные стадии разработки физической модели

на примере моделирования взрыва на выброс – взрывной

технологии, которая имеет важное значение в строительстве

крупных сооружений – плотин, каналов и т.д. При взрыве

на выброс

заряд закладывается таким образом, чтобы либо оптимизировать

процесс извлечения грунта, либо «уложить» выброшенный взрыовм

грунт нужным способом в нужном месте.

При моделировании таких взрывов предполагается, что к

рассматриваемому моменту ударноволновая стадия развития взрыва

завершена, а порода вокруг полости вплоть до свободной

поверхности разрушена. В силу этого, первоначальные прочностные

свойства породы не имеют значения. Разрушенная порода

представляется в виде зернистой среды, которая сопротивляется

сдвигу в соответствии с законом сухого трения.

Определяющим является процесс движения разрушенной

породы в поле силы тяжести под действием газообразных продуктов

взрыва. Поэтому в качестве начальных данных в модели выступают

343

размер камуфлетной полости и параметры котлового газа. В

качестве разрушенной породы при моделировании целесообразно

использовать заранее раздробленный материал с незначительным

сцеплением, например, кварцевый песок.

Поскольку и свойства материала и параметры источника в

модельном эксперименте буду радикально отличаться от натурных

условий, при разработке эксперимента необходимо контролировать

условия подобия.

Выпишем систему параметров для рассматриваемой модели.

Искомыми величинами являются размеры воронки: радиус R ,

глубина Н и объем V. Определяющими параметрами модели будут

характеристики источника взрыва, выбрасываемой породы и

внешних сил. В рамках принятой схемы начальные условия

определяются радиусом котловой полости r

, энергией газа в

полости E (или давлением P ), показателем адиабаты

, а также

глубиной взрыва W. Поскольку процесс выброса породы является

медленным, сжимаемостью среды можно пренебречь и

характеризовать разрушенную породу плотностью

коэффициентом внутреннего трения k

и сцеплением C,

учитывающим связь выбрасываемой породы с окружающим

массивом. В число определяющих параметров, естественно, нужно

включить ускорение силы тяжести g и атмосферное давление над

свободной поверхностью P

. В результате набор величин,

характеризующих процесс выброса в модели, будет состоять из семи

размерных и двух безразмерных параметров:

E, W, r

, g, P

, C, k

(9.22)

Из указанных определяющих параметров в условиях

сферически-симметричного источника взрыва можно образовать

следующие независимые безразмерные комбинации:

,,,,,

334

(9.23)

Как известно, в соответствии с теорией подобия, для подобия

двух явлений необходимо и достаточно, чтобы численные значения

344

безразмерных комбинаций, составленных из полного перечня

определяющих параметров, были одинаковы:

constconstk

const

====

,,,,

334

(9.24)

В общем виде зависимость основных размеров воронки

(например, радиуса) от начальных условий и свойств

выбрасываемой породы запишем:

);;;;;(

334

= (9.25)

Из зависимости (9.25) можно выделить два предельных

случая. В первом, когда может быть исключен из рассмотрения

параметр

, имеет место геометрическое подобие, т.е. энергия

газа в полости E ~ W

. Очевидно, что необходимыми и

достаточными условиями этого является:

PgW

и CgW

(9.26)

Это условие выполняется для взрывов малого масштаба.

В другом предельном случае, когда масштаб взрыва велик,

единственным определяющим параметром, содержащим энергию,

остаётся

. В этом случае подобные воронки, у которых R/W

= const, будут получаться при выполнении условия

const

т.е. энергия газа в полости должна возрастать пропорционально W

а не W

, как это следует из геометрического подобия.

Таким образом, для воспроизведения на модели

крупномасштабных взрывов на выброс необходимо, чтобы параметр

для модельных и натурных экспериментов оставался

345

неизменным. Чтобы величина параметра оставалась неизменной при

уменьшении линейного размера системы и сохранялось условие E ~

необходимо увеличить произведение

g. Возможности

увеличения плотности материала незначительны. Поэтому иногда

при моделировании прибегают к искусственному увеличению

ускорения силы тяжести при помощи центробежных и линейных

ускорителей. Если линейный размер модели в n раз меньше размера

воспроизводимого реального явления в натуре, то величина

требуемого ускорения a = ng. В случае линейного ускорителя

необходимые ускорения получают в результате резкого торможения

после плавного разгона, в частности, при падении модели с

различной высоты. При центробежном моделировании

испытываемый объект располагают на вращающейся установке

большого диаметра, где можно менять величину ускорения за счет

центробежной силы инерции. В обоих устройствах воронка выброса

образуется взрывом небольшой навески ВВ в грунте, помещенном в

специальную каретку. Присутствие волны сжатия и отраженных

волн требует включения в число определяющих параметров

динамических характеристик среды (сжимаемости и других упругих

свойств), которые свойственны волновым процессам. Поэтому,

строго говоря, эти методы не укладываются в рамки зависимости

(9.25). Возможности таких методов моделирования сильно

ограничены из-за кратковременности существования ускорения на

падающей платформе. Поэтому в свое время в США проводились

эксперименты в летающей лаборатории, где изменение величины

ускорения силы тяжести в диапазоне от 0,17g до 2,5g создавалось

на вираже самолета.

В ИДГ РАН (В.В.Адушкин, В.Н.Родионов, М.А.Садовский)

был предложен иной метод моделирования взрывов на выброс. В

качестве "взрыва" используется объём сжатого газа, который

имитирует взрывную полость. Как следует из зависимости (9.25),

для соблюдения условий подобия достаточно в модели уменьшить

величину размерных параметров P

, C, E, W, r

так, чтобы

безразмерные соотношения (9.23) в модельном эксперименте

совпали с их значениями в натурных условиях. С этой целью для

346

уменьшения величины Р

применено вакуумирование объема, в

который помещалась модель.

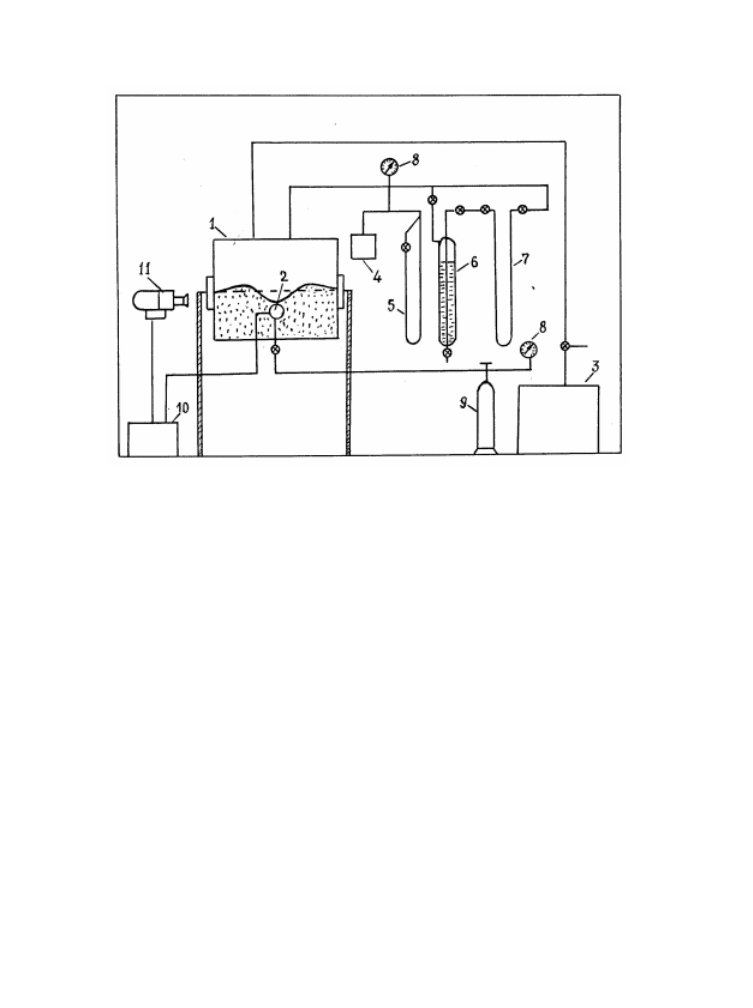
Рис.9.7 Схема и внешний вид установки для моделирования

экскавационного действия взрыва 1-вакуумная камера, 2-рабочий объем,

3-вакуумный насос, 4-вакууметр, 5-масляный манометр, 6-

диференциальный манометр, 7-ртутный манометр, 8-мановакууметр, 9-

баллон сжатого воздуха, 10-блок подрыва, 11-киноаппарат

Для снижения величины С в модели использованы сыпучие и

слабосвязанные материалы, у которых сцепление незначительно и

размеры зёрен малы по сравнению с глубиной взрыва W. Энергия

газа Е в модели устанавливалась в соответствии с глубиной взрыва

W так, чтобы соблюдались условия подобия (9.24). Радиус полости r

в модели подбирался из условия сохранения отношения W/r

Безразмерные параметры k

в модели и натуре близки. Таким

образом, изменяя контролируемым образом давление над свободной

поверхностью и сцепление грунта в модели, достигается

необходимое для того или иного масштаба взрыва соотношение

определяющих параметров, удовлетворяющих условиям подобия

(9.23) и (9.24).

347

Рис.9.8. Кинокадры развития выброса в модели

В частности, для моделирования взрывов на выброс крупного

масштаба, что было основной задачей разрабатываемой модели,

влияние параметров E/P

и E/cW

в модели сводилось к

линейному за счет глубокого вакуумирования и использования

сухого кварцевого песка. В этих условиях безразмерный параметр

становился определяющим. Чтобы реализовать эти условия,

массив сухого кварцевого песка был размещён внутри вакуумной

камеры. В массив песка на определенную глубину помещался объём

сжатого воздуха сферической формы, заключённый в эластичную

оболочку. После разрушения оболочки под действием внезапного

расширения газа происходил выброс песка, расположенного над

полостью, и получалась воронка. При этом безразмерные

комбинации определяющих параметров (9.23) соответствовали

условиям проведения крупномасштабного взрыва.

Схема установки и ее внешний вид показаны на рис.9.7, а

кинокадры развития выброса на рис.9.8.

348

При помощи описанной методики моделирования были

оптимизированы параметры проведения многих крупных взрывов,

предназначенных для возведения гидротехнических, селезащитных

и других сооружений.

9.3 Численное моделирование механического

действия взрыва

Теоретическое исследование процессов воздействия взрыва на

грунт с использованием сложных моделей деформирования

грунтовых сред возможно только численными методами. Выбор

того или иного численного метода решения конкретной задачи

зависит от ее специфических особенностей. К ним, прежде всего,

относятся особенности основных физических процессов,

характерных для изучаемого явления. Во многом выбор метода

зависит также

от используемых при решении задачи уравнений

состояния среды, граничных и начальных условий, наличия

контактных границ и т.п.

Очень важным вопросом, при построении численных схем,

является выбор системы координат расчетной сетки.

При решении многомерных задач нестационарной

гидродинамики наиболее часто используется представление

разностных уравнений в переменных Эйлера. Переменные Эйлера

удобны тем,

что они используют неподвижную (обычно

прямолинейную) расчетную сетку. В переменных Эйлера

координаты отвечают фиксированным точкам (ячейкам) в

пространстве, и рассматривается движение среды через эти ячейки.

Достоинством эйлеровых схем является возможность расчета в

областях с большими деформациями. Наиболее существенные

недостатки связаны с трудностями в расчете контактных границ и

ошибки при моделировании процессов

с малыми изменениями

параметров.

Раздел написан д.т.н. А.М.Будковым

349

Для решения задач механики твердого деформируемого тела

предпочтительным является использование численных схем в

переменных Лагранжа, где координаты связаны с движением среды

в пространстве (аппроксимирующая сетка движется со средой) и

отвечают фиксированным точкам в среде. К достоинствам

лагранжевых численных методик относятся повышенная точность

расчета фронтовых параметров, удобство описания контактных

границ, возможность использования

сложных моделей

деформирования среды, к недостаткам — трудности расчета в

областях с большими деформациями.

В ряде случаев целесообразно использовать совместное

эйлерово-лагранжево представление. Совместные эйлерово -

лагранжевы (СЭЛ) методы расчета позволяют при решении

отдельных задач избежать недостатков как лагранжевых, так и

эйлеровых численных схем.

Рассмотрим более подробно вопросы, связанные с

использованием лагранжевых

численных методик для

математического моделирования волновых процессов,

сопровождающих воздействие взрыва на грунт. Преимущества

схемы в переменных Лагранжа особенно ясно проявляются при

решении задач с контактными границами (взрыв вблизи

поверхности грунта, учет неоднородностей строения грунтового

массива и т.д.), а также при использовании сложных моделей

деформирования грунтовых сред, учитывающих предысторию

процесса деформирования

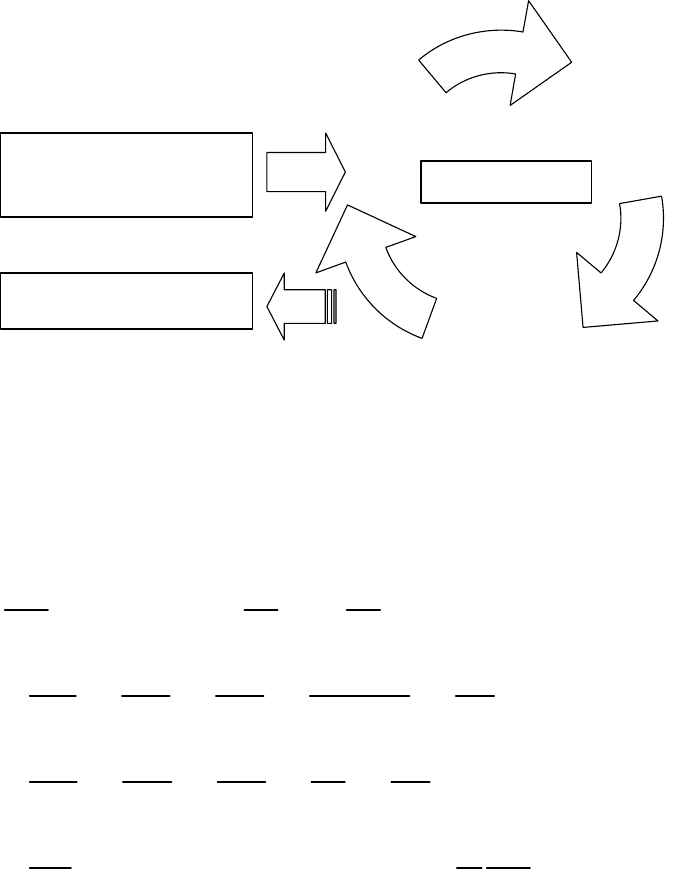
Диаграмма, показывающая последовательность операций при

проведении расчетов с использованием явной лагранжевой

численной методики представлена на рис.9.9. Типичная программа

состоит из блока построения расчетной сетки и задания начальных и

граничных условий, основного расчетного блока, циклически

пошагово выполняющего интегрирование уравнений движения,

блока формирования выходных данных (запись временных эпюр

параметров движения и напряженного

состояния среды, контроль

интегральных параметров — энергии, импульса и пр.) и блока

графической обработки результатов, позволяющего представлять

результаты расчетов в наглядной и удобной для анализа форме.

350

Уравнения, описывающие поведение грунтовой среды в

осесимметричном случае, имеют вид:

0, , ,

2 0,

rrrrz rrzz

zzzrzrz

rr rr zz zz rz rz

ddrdz

divu u u

dt dt dt

du s s s s P

dt r z r r

du s s s P

dt z r r z

dPd

se se s e se

dt dt

θθ θθ

ερ

+== =

∂∂ +∂

−−− +=

∂∂ ∂

−−−+=

∂∂ ∂

−−− − − =

&& & &

(9.27)

где t — время; r , z ,

— цилиндрические координаты (z — ось

симметрии);

— плотность; u

— компоненты вектора скорости

Расчет

параметров

напряженного

состояния

Формирование

выходных

данных

Расчет

ускорений,

скоростей,

смещений

Цикл по времени

t=t

n+1

Построение расчетной

сетки, задание начальных и

граничных условий

Графическая обработка

результатов

t=t

Рис.9.9 Последовательность операций (явная численная схема в

переменных Лагранжа)