Кочарян Г.Г. Деформационные процессы в массивах горных пород

211

состояния, трение может радикально уменьшиться в начале и затем

восстановиться до постоянной величины (кривая (2) на рис.5.19) или

уменьшаться постепенно до постоянного уровня (кривая (3)).

В большинстве приложений используется скачок напряжений,

усредненный по всей площади

A разломной плоскости.

∫

Δ=Δ

A

ss

dS

A

σσ

1

(5.28)

Ограниченное разрешение сейсмологических методов обычно

допускает определение лишь средних перемещений вдоль

разломной плоскости. Эти значения используются, чтобы вычислить

средний скачок напряжений. В таком приближении из статической

модели трещины можно получить выражение для среднего скачка

статических напряжений:

Λ

Δ

=Δ

u

C

s

μσ

, (5.29)

где

uΔ – среднее смещение по разрыву, Λ- характерный размер

разрыва, С - константа, зависящая от геометрии разрыва.

Для круговой трещины

Λ=a – радиус трещины, C=7π/16.

Для длинного разрыва шириной

D в бесконечном

пространстве, Λ=D/2, а C=2/π (сдвиг) или С=4(λ+μ)/ π(λ+2μ) (разрыв

со смещением по падению).

Из (5.29) и (5.26) легко получить выражение скачка

напряжений через сейсмический момент:

A

CM

s

Λ

=Δ

0

σ

. (5.30)

Например, для кругового разрыва радиусом

a имеем:

3

0

16

7

a

M

s

=Δ

σ

(5.31)

Напомним, что и величину сейсмического момента, и

характерный размер источника можно определить из спектра

колебаний. Величина M

0

пропорциональна амплитуде спектра в

низкочастотной области, а характерный размер вычисляется из

212

угловой частоты. Таким образом, можно оценить скачок

напряжений в очаге.

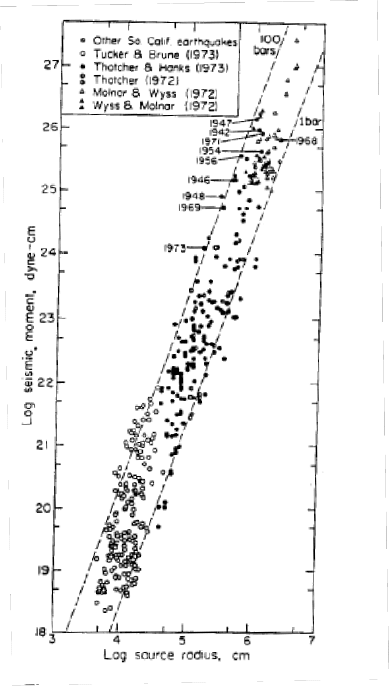
Рис.5.20 Связь между сейсмическим моментом и характерным

размером очага (

Scholz, 1990)

На рис.5.20 показана связь сейсмического момента и радиуса

для небольших землетрясений. Понятие «маленького» и «большого»

землетрясения здесь употребляется в том смысле, что для малого

масштаба событий разрывы распространяются внутри верхней части

коры и их можно рассматривать как трещины в бесконечной среде.

Величина Δσ вычислена для модели кругового разрыва по

213

соотношению (5.31). Пунктиром показаны постоянные уровни

скачков напряжения 1 атм и 100атм. Как видно, амплитуда скачка

напряжений, определенная по экспериментальным данным (точки)

заключена между этими значениями.

Как видно из (5.31), точное определение размера источника

имеет большое значение для корректной оценки скачка напряжений

– двукратная ошибка в определении размера приводит к ошибке в

расчете

s

σ

Δ

почти на порядок.

5.2.5 Баланс энергии

Рассматривая землетрясение, как распространяющуюся

трещину сдвига, можно аналогично трещине Гриффитса записать

уравнение баланса энергии:

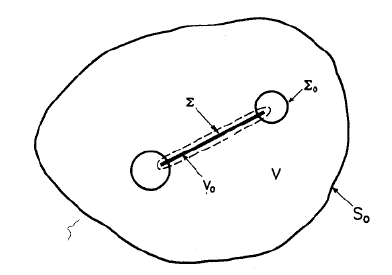
Рис.5.21 Области интегрирования

fkse

UUUUWU

+

−

= )( , (5.32)

где

W-работа внешних сил, U

e

– изменение внутренней энергии

деформации,

U

s

– поверхностная энергия, необходимая для создания

трещины,

U

k

- кинетическая энергия, U

f

– работа против сил трения.

В динамическом случае мы можем выразить условие

равновесия (1.8)

0/

=

dCdU , как производную по времени и

записать энергетический баланс в виде:

214

fkse

UUUUWU

&&&&&&

++++−== )(0

, (5.33)

где слагаемые представляют следующие интегралы по областям,

показанным на рис.5.21

)34.5(

2

1

)34.5(

2

1

)34.5(2

)34.5(

2

1

0

2

дdV

t

U

гdSnu

t

U

вdSnu

t

W

бdS

t

U

adVu

t

U

VV

ijije

jiijf

S

jiij

s

V

ik

∫

−

Σ

⋅

∂

=

⋅

∂

=

⋅

∂

=

∂

=

⋅

∂

=

εσ

σ

γ

ρ

&

,

где, как обычно,

ρ – плотность, γ – удельная поверхностная энергия,

u

i

– перемещение, σ

ij

и ε

ij

– компоненты тензоров напряжений и

деформаций,

Если проинтегрировать (5.34) по всему времени разрыва, то

каждый член превратится в изменение соответствующей части

энергии.

При рассмотрении достаточно большого объема, слагаемое для

работы на внешней границе (5.34в) становится малым, и мы можем

записать выражение для излученной сейсмической энергии

E

s

в

виде:

sfeks

UUUUE

Δ

−

Δ

−

Δ

−

=

Δ

≡

(5.35)

С достаточной степенью общности, землетрясение можно

представить как процесс высвобождения напряжений на

поверхности разлома

Σ

.

Будем полагать, что начальные сдвиговые напряжения на

плоскости разлома

0

σ

снижаются до величины динамического

трения

0f

σ

, т.е.

01 f

σ

=

(см.рис.5.20). При этом динамический

215

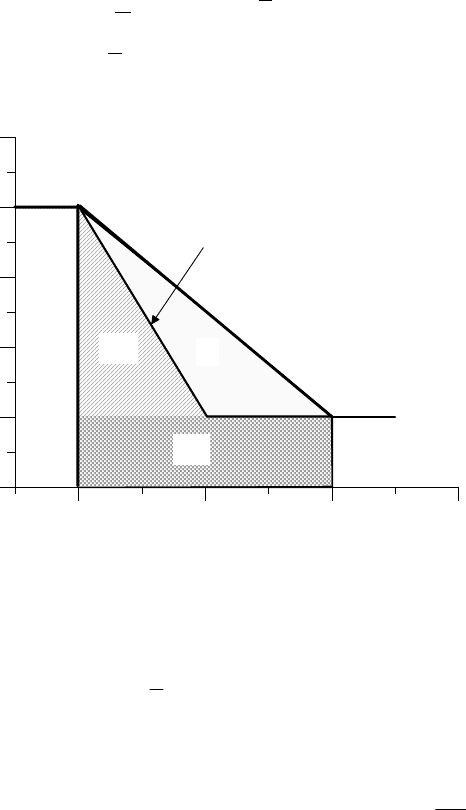
процесс заканчивается после смещения D (рис.5.22). В ходе этого

процесса и излучается сейсмическая энергия

E

s

.

Если в ходе образования разрыва сдвиговые напряжения

изменились с σ

0

до σ

1

, то изменение внутренней энергии деформации

составляет:

AuU

e

Δ+−=Δ )(

2

1

10

σσ

, (5.36)

где, как и прежде,

u

Δ

– среднее смещение по разрыву, а А –

площадь разлома.

0

Относительное перемещение берегов

Напряжение

σ

0

σ

1

D

(2)

σ

f0

D

c

σ

f

(u)

E

s

Δ

U

s

Δ

U

f

Рис.5.22 Баланс энергии при образовании разрыва

На рис.5.22 графически,

e

U

Δ

на единицу площади выглядит в

виде площади трапеции (

Du

≅

Δ

).

Положим, что трение постепенно снижается в процессе

скольжения, как в

rate - state модели, достигая минимального

значения при величине относительного перемещения D

c

.

Таким образом, мы определяем среднее трение

f

σ

как:

216

∫

=

D

ff

duu

D

0

)(

1

σσ

, (5.37)

где

u – перемещение вдоль плоскости разлома.

Полная диссипированная энергия

DAduuAUU

f

D

fsf

σσ

=⋅=Δ+Δ

∫

0

)(

. (5.38)

Рис.5.22 показывает распределение разных видов энергий. Площадь

под трапецией представляет полное изменение внутренней энергии

деформации

e

U

Δ

. Площадь под кривой, обозначенной как

f

σ

, есть

полная диссипированная энергия. Таким образом, в соответствии с

(5.35), излученная сейсмическая энергия

s

E есть площадь

треугольника, залитого точками.

DAUE

fes

σ

−

Δ

−

=

. (5.39)

Энергия

s

U

Δ

, затраченная на трещинообразование, показана

на рис.5.22 одинарной штриховкой, а энергия

f

U

Δ

, затраченная на

преодоление трения, двойной штриховкой. Таким образом, полная

диссипированная энергия

DA

f

σ

может быть разделена на

f

UΔ

и

фрикционную энергию,

f

U

Δ

.

Как видно из рис.5.22 :

s

ss

UDSUDAE Δ−

Δ

=Δ−

−

=

22

10

σ

. (5.40)

Если, для простоты предположить, что напряжения на разрыве

изменяются скачком, то поверхностная энергия оказывается

незначительна, т. е. получаем:

DAE

s

σ

Δ≈

2

1

, (5.40а)

Из (5.40) можно заключить, что сейсмическое излучение

содержит только информацию, касающуюся изменения напряжений

в ходе землетрясения и не содержит информацию об абсолютной

величине напряжений.

217

Из (5.26) и (5.40а) получаем связь сейсмической энергии и

сейсмического момента:

0

2

ME

s

μ

σ

Δ

= . (5.41)

5.2.6 Сейсмическая эффективность

Вопрос о распределении энергии в очаге представляет собой

фундаментальную проблему. Из параметров сейсмических

колебаний определяется лишь сейсмическая энергия – часть полной

энергии, идущей на излучение сейсмических волн. Согласно (5.40)

сейсмическое излучение не содержит информации об абсолютной

величине. В тоже время, работа, выполняемая при

разломообразовании, зависит от уровня напряжений.

Отношение величины сейсмической энергии к

полному

изменению внутренней энергии системы называют

сейсмической

эффективностью источника

:

e

s

U

E

Δ

=

η

. (5.42)

Соответственно, из (5.36) и (5.40а) получаем:

10

σσ

σ

η

+

Δ

=

, (5.43)

т.е. сейсмическая эффективность источника зависит от полных

напряжений и не может быть определена из одних лишь

сейсмологических наблюдений.

Если предположить, что скачок напряжений составляет 5-10% от

среднего напряжения, то η~0.02÷0.05.

С другой стороны, если предположить, что скачок

напряжений постоянен (скажем разница между статическим и

динамическим трением), то величина η должна

уменьшаться с

увеличением полных напряжений.

218

Обычно полагают, что величина сейсмической

эффективности для коровых землетрясений составляет η~0.01.

Отношение

ss

s

R

UE

E

Δ+

=

η

(5.44)

называется излучательной эффективностью источника.

Излучательная эффективность

R

η

отличается от

сейсмической эффективности (5.42). Как обсуждалось выше,

e

UΔ

не может быть определен сейсмологическими методами. Поэтому

сейсмическую эффективность трудно расчитать. Поскольку

sse

UEU Δ+≥Δ , то

η

≥

R

. Если 1

≈

R

η

участок формирования

разрушения не существенен и процесс происходит в стабильном

режиме. Если же

1

<

R

η

, то доминируют динамические процессы

микроразрушения.

Комбинируя (5.44) и (5.40) мы получаем соотношение между

R

η

и

наблюдаемыми сейсмологическими параметрами.

e

s

R

ˆ

2

σ

μ

η

Δ

=

(5.45)

0

ˆ

M

E

e

s

=

(5.46)

есть излученная энергия, нормированная на сейсмический момент.

Этот параметр по некоторым данным увеличивается с ростом

магнитуды.

219

5.2.7 Объем очага, время подготовки

землетрясения и распределение событий по

глубине

Иногда бывает удобно использовать такое понятие, как

«объем очага» землетрясения. Тсубои (1961) предложил

использовать для оценки этого параметра площадь проекции зоны

афтершоков на поверность, идентифицируя эту область с объемным

очагом динамического события. При этом, объем очага V

оценивается по соотношению:

2/3

SV =

. (5.47)

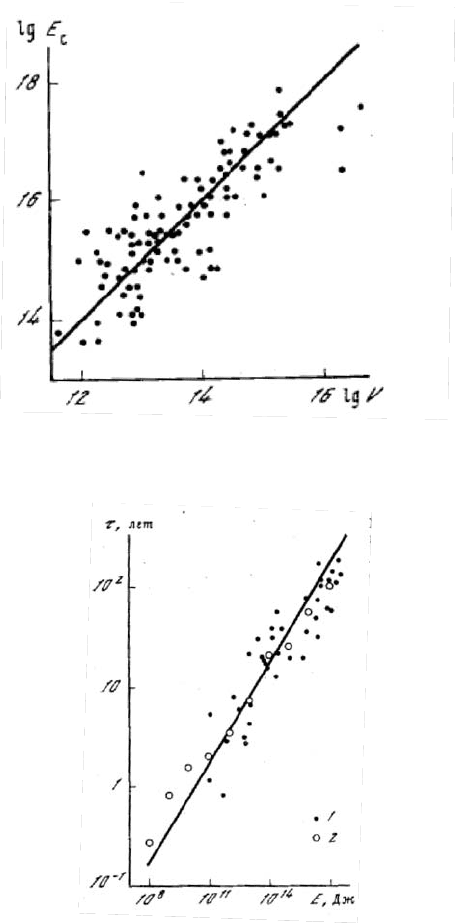
Обработка результатов наблюдений (рис.5.23) показывает, что

существует корреляционная связь между сейсмической энергией

события

E

c

и объемом очага, выражаемая соотношением:

2lglg

+

=

VE

c

. (5.48)

Отсюда следует, что объемная плотность энергии в очаге примерно

постоянна и составляет величину

E/V~100Дж/м

3

.

Если ввести параметр Ω – среднюю скорость «подкачки»

энергии в очаг землетрясения, то средний поток энергии через

поверхность очага S будет:

2

LS Ω≅⋅Ω=Φ (5.49)

Соответственно, накапливаемая упругая энергия за время t:

tLE

2

Ω≅

(5.50)

Обозначая ε

k

среднюю «критическую» плотность энергии в

очаге, а τ время достижения этой «критической» плотности (

время

подготовки землетрясения

), получаем из (5.49) и (5.50)

τε

23

LEL

k

Ω≅≅ , или L

k

Ω

≅

ε

τ

, т.е время подготовки

землетрясения пропорционально характерному размеру, т.е. корню

кубическому из энергии землетрясения:

3/1

~~ EL

τ

, (5.51)

220

Рис.5.23 Зависимость сейсмической энергии (Дж) от объема очага.

Рис.5.24 Зависимость времени сейсмического цикла от энергии

землетрясения

Кочарян Г.Г. Деформационные процессы в массивах горных пород

Подождите немного. Документ загружается.