Кочарян Г.Г. Деформационные процессы в массивах горных пород

Подождите немного. Документ загружается.

191

Для количественного описания поля смещений, возникающего

при подвижке по разлому, применяются различные модели.

J.Steketee (1958) предложил использовать для этих целей развитый

аппарат теории дислокаций, назвав этот подход «Упругая теория

дислокаций». Принципиальное отличие от кристаллографических

дислокационных моделей (см. раздел 1.2) состоит в том, что

последние по сути своей дискретны, а «сейсмологическая»

дислокация является непрерывной.

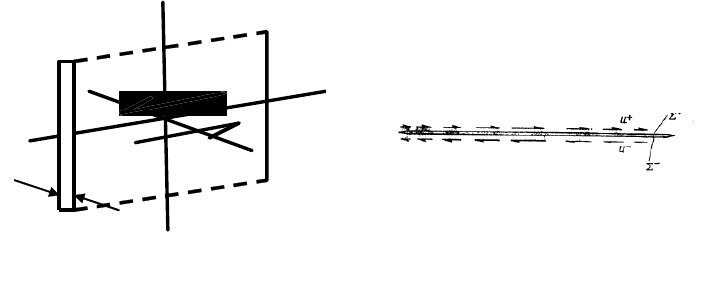
В простейшем виде сдвиговую

дислокацию в пространстве можно описать следующим образом.

Вначале внутри упругого тела производится надрез Σ, в результате

чего образуется новая поверхность. Затем, к двум берегам разреза

прикладывается тангенциальное относительное перемещение и

берега вновь склеиваются (рис.5.4). После такой операции в теле

вновь достигается непрерывность напряжений, но возникают

внутренние деформации

из-за разрыва смещений на Σ. При этом,

никаких внешних сил к системе не приложено. Картина

распределения деформаций в среде зависит только от конфигурации

поверхности и распределения смещений на ней. В случае малых

деформаций всегда можно найти систему внешних сил, которая

порождает поле эквивалентное поле смещений в среде без введения

разреза (Теорема об эквивалентности сил и дислокаций). Строгое

-a

2ε

Рис.5.4. Схематичное изображение сдвиговой дислокации в упругом

теле (справа – вид в плане)

192

математическое обоснование этого утверждение приводится в курсе

«Теории упругости» Л.Д.Ландау и Е.М.Лифшица. Здесь же мы

приведем упрощенное изложение.

Рассмотрим сдвиговую дислокацию на малом элементе Σ

плоскости (

) в декартовой системе координат (x

) (рис.5.4).

Обозначим перемещения берегов

u и

−

u . При этом будем

полагать, разрыв имеется только на компоненте смещений u

, а

компоненты u

и u

– непрерывны.

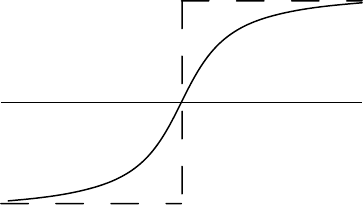
В рамках идеальной упругости заменим ступенчатый разрыв

смещений на гладкую функцию (рис.5.5)и найдем систему сил,

которая даст подобное распределение смещений. Штриховая линия

на рис.5.5 может считаться предельным случаем непрерывного

изменения смещений при ε→0, где . ε – малое расстояние от

элемента Σ.

−

Рис.5.5 Сглаживание распределения смещений в окрестности

сдвиговой дислокации

Закон Гука в упругом изотропном теле задается, как известно,

соотношениями:

193

(

)

()

()()

[]

()()

[]

()()

[]

21122112

13311331

32233223

3333

2222

1111

,/2

xuxu

∂∂+∂∂==

∂∂+=

∂

μττ

μλθτ

λθ

, (5.10)

где

)/()/()/(

332211

xuxuxu

∂

∂=

, а λ и μ – постоянные

Ламе.

Уравнения равновесия выделенного элемента:

0)/()/()/(

3333223113

2332222112

1331221111

=+∂∂+∂∂+∂∂

∂

∂∂

fxxx

ρτττ

, (5.11)

где

– соответствующая компонента объемной силы на единицу

массы.

В предположении, что резко в окрестности Σ меняется только

, а остальные перемещения меняются медленно, отлична от 0

только одна производная

∂

, т.е. из всех компонент напряжений

остаются только:

2112

∂

μττ

. (5.12)

Соответственно, силы, которые надо приложить, чтобы

вызвать искомое поле смещений:

(

)

()

1122

2211

∂∂−=

∂

−

τρ

(5.13)

Если задать в (5.12) перемещение в виде гладкой кривой, как

показано на рис.5.5, то можно получить изменение напряжений τ

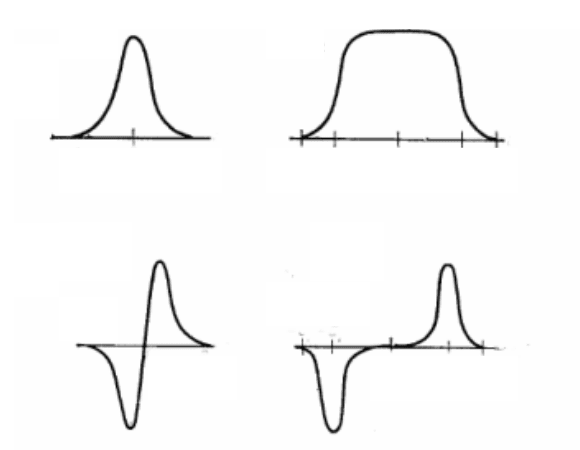
194

вдоль осей x

и x

, которое будет выглядеть в виде, показанном на

рис.5.6а, а, соответственно, изменение сил

ρf

и ρf

, на рис.5.6б.

ρf

-ε 0 ε

0 ε

-ε

-c -a

0 a

-c -a

Рис.5.6 Пространственное изменение касательных напряжений (а) и

приложенных сил (б)

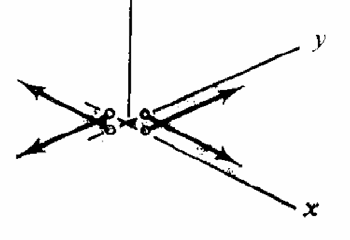
Устремляя к нулю линейные размеры ε→0, легко видеть, что

по мере стремления перемещения к ступенчатой функции (рис.5.7

сплошная линия стремится к пунктиру), силы стремятся к двойной

паре сил.

Легко видеть, что объемные силы имеют момент относительно

оси

. Рассчитывая моменты, можно показать, что момент

прикладываемых сил выражается соотношением:

UAM

, (5.14)

где

μ – модуль сдвига среды, U – среднее значение величины Δu

на

площадке Σ, общая площадь которой равна

195

Рис.5.7. Модель двойной пары сил

Таким образом, поле смещений, вызванное сдвиговой дислокацией,

можно выразить через суперпозицию элементарных точечных

источников типа двойной пары сил, распределенных по поверхности

разлома.

5.2.2 Фокальный механизм

Важная информация о характере движения в очаге

землетрясения может быть получена из анализа характера

вступлений сейсмических волн. Полярность первого импульса P-

волны, излучаемого при землетрясении, принимает одно из двух

противоположных направлений – смещение направлено либо к

эпицентру (что соответствует сжатию в очаге, либо от него

(расширение). Как известно, при взрыве в однородной

среде первое

вступление всегда направлено от источника, а распределение

амплитуд сферически симметрично.

Еще в начале XX века было обнаружено, что распределение

знаков вступлений при землетрясениях не случайно, а носит

закономерный характер.

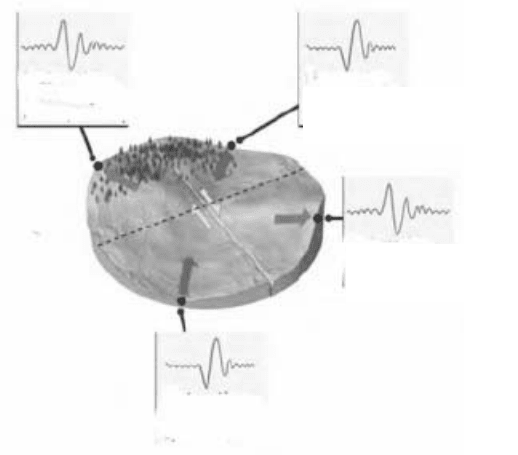
На рис.5.8 показано распределение смещений поверхности от

вступления Р-волны. Достаточно легко провести две прямые линии,

пересекающиеся в центре, отделяющие области

сжатия от

растяжения.

196

первое вступление

к эпицентру

первое вступление

от эпицентра

Рис.5.8 Распределение знаков смещений поверхности при

вступлении Р-волны

Такое распределение называется «

квадрантным», а линии,

разделяющие квадранты – нодальными линиями. Вдоль них

амплитуда сигнала приближается к нулю. Для того, чтобы объяснить

подобное распределение вступлений, разрабатывались

теоретические модели очага с разными системами сил, действующих

в точечном источнике. Наибольшее распространение получила

модель двойной пары сил, показанная на рис.5.7. В этой модели

предполагается, что в точечном источнике

действуют две пары сил,

каждая из которых за короткий промежуток времени возрастает от

нуля при t=0 до определенного уровня, после чего остается

постоянной. При этом моменты этих пар сил относительно оси Z

равны и противоположны по направлению. Поле перемещений

такого источника записывается в виде:

197

()

⎥

⎦

⎤

⎢

⎣

⎡

−

∇∂∂

∂

−=

⎥

⎦

⎤

⎢

⎣

⎡

∇

∂

+−

∂∂

∂

−=

⎥

⎦

⎤

⎢

⎣

⎡

∇

∂

+−

∂∂

∂

−=

ψϕ

πρ

ψψϕ

πρ

ψψϕ

πρ

zyx

xyx

yyx

(5.15)

где

u, v, ω – компоненты перемещений в направлениях x, y, z; ρ –

плотность;

))((

));((

−=−=

ψϕ

при этом сила,

действующая в начале координат:

)(

tf =

Пренебрегая в (5.15) членами

1/r

и выше, переходя к полярным

координатам, можно получить выражения для поля перемещений:

ϕθ

πρ

ϕθθ

πρ

ϕθ

πρ

2cossin

,2sincossin

,2sinsin

⎟

⎠

⎞

⎜

⎝

⎛

−

′

⎟

⎠

⎞

⎜

⎝

⎛

−

′

⎟

⎠

⎞

⎜

⎝

⎛

−

′

(5.16)

Из этих выражений легко видеть, что смещения в продольных

волнах определяются выражением

, а в поперечных волнах u

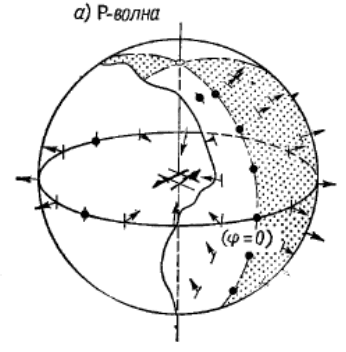
198

Рис.5.9 Смещения в P-волне, излучаемой источником типа двойной

пары сил

Второй особенностью приведенного решения является

зависимость амплитуды и направления перемещения от азимута.

На рис. 5.9 показана картина перемещений в P- волне от

источника типа двойной пары сил. Распределение квадрантное с

нодальными линиями соответствующими φ=0, π/2, π, 3π/2. Такое

распределение вступлений P-волн позволяет разработать метод

определения плоскости разлома в очаге.

Если вокруг эпицентра расположено

много станций, то, определив

направления вступлений, достаточно просто отделить области

сжатия от областей растяжений и оценить направление сдвига в

источнике. Однако такая ситуация встречается достаточно редко. В

противном случае применяется следующий метод.

Окружим очаг сферой единичного радиуса, которую иногда

называют

сферическим очагом или референс -сферой (рис. 5.10).

Сейсмический луч, приходящий на станцию

S, выходит из сферы

под некоторым углом выхода

i, который является функцией

эпицентрального расстояния

Δ. Если в точке S' на сфере задается

знак смещения на фронте Р-волны, зарегистрированный в S; тогда

представляет данные станции S.

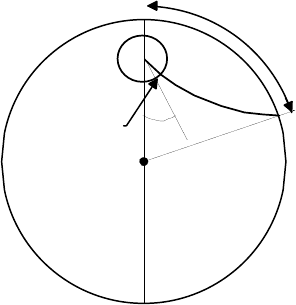
199

Рис.5.10 Сейсмический луч (OS) и референс-сфера внутри Земли. O –

фокус, Е – эпицентр, S

– проекция на поверхность референс-сферы.

Сейсмический луч изображен вогнутым, так как скорость

сейсмических волн увеличивается с глубиной

Технически, сначала определяют азимут φ

и Δ - расстояние от

станции до эпицентра. Затем, используя Δ, определяют угол выхода

из очага. Это делается при помощи моделей распределения

скоростей в Земле.

Повторив эту процедуру для всех станций, на которых получены

данные определенного сейсмического события, мы получим

исчерпывающую картину излучения волн из очага. Начальный

характер упругой волны должен в принципе остаться неизменным

при ее распространении, т. е. данные на сферическом очаге

должны

верно представлять первоначальную полярность излучаемых волн.

Предположим, что механизм очага представляет собой двойной

диполь. Тогда сферический очаг должен быть разделен парой

ортогональных плоскостей на четыре области, в каждой из которых

в зависимости от знака первого импульса наблюдается либо сжатие,

либо растяжение. Одна плоскость соответствует реальному

направлению разлома в очаге, а

другая является сопряженной (см.

200

рис.5.8). Нужное направление обычно определяют из геологических

данных.

При помощи метода стереографических проекций картину

излучения на сфере проектируют на окружность, получая, так

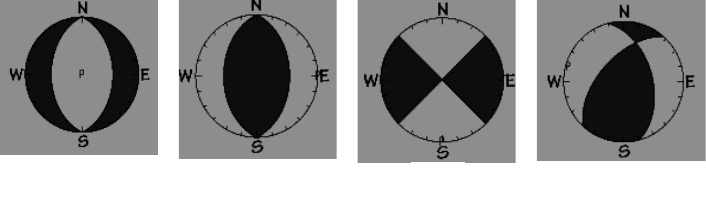
называемые, разломно-плоскостные диаграммы (рис.5.11), по

характеру которых определяют как ориентацию плоскости разлома в

очаге, так и вид подвижки (сдвиг, сброс, надвиг или их комбинация).

5.2.3 Спектр волн, излучаемых при

землетрясении

Выше мы рассмотрели поле смещений от неподвижной

дислокации в упругой среде (5.16). На самом деле, в очаге

землетрясения имеет место распространение разрушения.

Зародившись в какой-то точке, разрыв распространяется со

скоростью, не превышающей скорость распространения продольных

волн. (На самом деле физический предел скорости распространения

разрушения соответствует скорости распространения релеевских

волн). Обычно скорость

распространения разрушения бывает близка

к скорости распространения поперечных волн

, хотя иногда имеет

значительно более низкие значения. Таким образом, источник

сейсмических волн при землетрясении упрощенно можно

а б в г

Рис.5.11 Типы разломно-плоскостных диаграмм а- сброс; б – надвиг; в –

сдвиг; г – комбинация сдвига и сброса. Светлые области соответствуют

растяжению, темные – сжатию