Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

Так как дрейфовая подвижность в слабом поле имеет вид

= (42.32)

то •

= (42-33)

т. е. холлова подвижность, определяющая угол Холла, пропорцио-

нальна дрейфовой подвижности..

Рассмотрим величину σ

. С учетом (42.27) (42.12) ее можно запи-

сать в виде (слабое поле!)

= е

К'п [1 +

]

^ е

Кц =

CQ.

(42.34)

Из (42.18) следует

= 7?σ

. (42.35)

Определив экспериментально R и σ

и взяв шг произведение, полу-

Если известен механизм рассеяния, то по μ

можно опре-

делить = а по —концентрацию носителей заряда и их знак;

благодаря этому эффект Холла является одним из важнейших мето-

дов исследования полупроводников.

Для вырожденных пролупроводников и металлов

Α-ίϋλ- ΙϋΏ—1 /42 36^

поэтому

μ" = μ,; = (42.37)

2. Сильные поля. В сильных полях

/ * \ /-./f^-'Nj.

& _ \1 + цЦР/ _ \ U*V / В» _ _} •,

iy4

оол

τ \~//*τ»\-ι\ ι >

(42

\1+μ?Β»/ \

\т*>) /ψ \х/

(42.39)

Учитывая (42.39), перепишем выражение (42.19) для сильного поля

При сколь угодно больших полях первое слагаемое знаменателя

•40) может быть много меньше второго, поэтому

261

т. е. в сульном магнитном поле коэффициент Холла не зависит от

механизма рассеяния (А=1), как в вырожденном полупроводнике.

Сравнивая выражения (42.41) и (42.28) для R в сильных и слабых

полях, мы видим, что R зависит от В: с ростом поля величина R

А 1

уменьшается от — до —. Переход происходит в области полей, для

которых

^1. (42.42)

Рассматривая отношение величин R при малых полях

—

— и

при

больших полях

— /?оо

—, легко получить величину А:

А = (42.43)

В заключение заметим, что в понятие сильного или слабого поля

входит подвижность носителей заряда с данной энергией. Но если

τ = τ

и р^> 0, то условие μ

<^1 формально не может быть

выполнено ни при каких полях для всех возможных значений энер-

гии. Однако это не так. Как число, так и вклад носителей заряда

больших энергий в образование усредненных значений времен релак-

саций будут незначительными. Поэтому условия (42.24) и (42.25)

необходимо понимать в том смысле, что они должны выполняться,

если под μ понимать дрейфовую (или холлову) подвижность, т. е.

оценкой величины поля должны быть условия

μ^β

< 1;μ*5

> 1. (42.44)

Рассмотрим пример. В InSb м

/(В-с)"

, поэтому слабое

поле должно удовлетворять условию В

<^ 1/64 = 0,015 и θ<0,1Τ =

= 1000 Гс. В р

—

Si μ^^Ο,Οδ^^ и практически достижимые поля

являются слабыми.

Резюме § 42

1. Из уравнения для плотности тока

j =

/(ίιΕ

+ К'

[ЕВ] (42 Л р)

с «граничными» условиями

j = (/*, 0, 0) (42.2Р)

вытекает выражение для поперечного поля Е

—

поля Холла:

= -^B

= -RB

, (42.Зр)

откуда для коэффициента Холла

' (42.4Р)

262

2. Подвижность Холла μ

определяет напряженность холлова

поля через напряженность электрического поля E

вызывающего

ток, и индукцию магнитного поля В = В

= β%-, (42.5р)

Я.

угол Холла φ определяется холловой подвижностью μ

Холлова подвижность выражается через кинетические .коэффици-

енты:

/ * . \

+ (42.7р)

т* /С

т* / τ \

v г/

3. В слабом магнитном поле

^σ

βημα)

= (42.8р)

4. В сильном магнитном поле

= b = (42.9р)

т. е. коэффициент Холла не зависит от механизма рассеяния.

5. Механизм рассеяния влияет на значение R посредством мно-

жителя А; в слабом поле холл-фактор

А = (42Л0р)

3π ^ 315π

что дает γ при рассеянии на тепловых колебаниях решетки, -^г

при рассеянии на ионах примеси и 1 в вырожденных полупровод-

никах и металлах. В сильном поле А=1.

6. Концентрация носителей заряда

(42.11р)

§ 43. ЭФФЕКТ ХОЛЛА В ВЕЩЕСТВЕ С НОСИТЕЛЯМИ ЗАРЯДА

НЕСКОЛЬКИХ ТИПОВ

В этом параграфе рассмотрим эффект Холла β однородном полу-

проводнике в изотермических условиях в предположении, что в нем

имеется несколько типов носителей заряда. Это может быть собствен-

ный полупроводник, полупроводник в области смешанной проводи-

ли или полупроводник в области примесной проводимости при

263

наличии носителей заряда нескольких масс, например, ρ

—

Si или

—

Ge, в которых имеются легкие и тяжелые дырки.

Для носителей заряда α-вида можно записать обычное выраже-

ние для тока:

+ (43.1)

Полный ТОК

Ί=2

JA=

(Σ

ЕЖП(Α)

)

Ε+

(Σ 5 T

EΒ

Ί· (43.2)

a / \ a

Все выражения предыдущего параграфа должны быть справед-

ливы, если вместо К η к К η подставить соответствующие суммы.

Рассмотрим решение уравнения (43.2) для ограниченного полупро-

водника:

В = (О, В, 0); E = (E

,Ey,E

); [EB] = (-E

B, 0, Е

В); j = (/*, 0,0).

(43.3)

Коэффициент Холла R определяется условием (42.15). Найдем

и = (У *&*ίκα>) Е

- (У ^ /Г

и(

а)) (43.4)

\ а ' \ а

/у

= 0, £^ = 0; (43.5)

И=^ <«>) +(2 %

П <А>

)

ΒΕΧ=

°·

(43

Из (43.6) определим Е

Это выражение можно представить аналогично (42.9), если опре-

делить подвижность Холла μ" тем же условием:

tg φ = ξ* = — μ»Β. (43.8)

Тогда

(Σ4

ΐ2(Α)

)

μ"

= L

a^n (a) j

= -μ

ΒΕ

. (43.Ю)

(43.9)

264

Выразим

через

[ΖΛΚ

nia)

= ОвЕ

, (43.11)

(Σ

n (α)

)

Εχ

+ /ν —\

—

aK'n

(α)^

{1 + β

} (43.12)

где

есть проводимость в направлении тока при наложении магнитного

поля. Из (42.15), (43.10) и (43.11) можем записать

D E

\х

ВЕ

..„ .

Во

- - ν ^

άΛό

что совершенно аналогично (42.17), однако выражения для σ

и μ

в данном случае другие. Подставляя их выражения (43.12) и (43.9),

получим

(У* г

. У ^ [I* ™

(43.14)

Подставляя в (43.14) выражения (29.27) для кинетических коэф-

фициентов, запишем

Уеп / \

+μ«

β2

Если в веществе имеется один тип носителей заряда, то (43.15)

переходит в (42.23).

1. Слабые поля. Рассмотрим слабые поля: μαβ

<^1, при этом

неравенство должно удовлетворяться для всех типов носителей заряда,

и прежде всего для носителей заряда с максимальной подвижностью.

Пренебрегая величиной μ^

по сравнению с единицей во всех чле-

нах и вторым слагаемым в знаменателе по сравнению с первым

слагаемым, получим

Γ^Ίt>

(43Л6)

|2J ^α(μα)

265

но

поэтому

где

<Μ

>=^<Τ

> = Μ*Χ (43.17)

<μα> = φ (rt) = (и^) ^ = ^^Α

, (43. ι

Σ*

μ2α Σ

απ£

(Σ^αμ,ή

2 = (43Л9)

ο = —· (43.20)

α 2J

Рассмотрим выражение (43.19) для двух типов носителей заряда:

η _ *ι/*ιΑιμ£ι + β

^2Α

μ^2 /до

* (ein&

μ„

)

Если полупроводник имеет смешанную проводимость, то, полагая

= п; п

= р; е

= е

, е

= е

; μ^ι = μ

; μ<*2=μρ; ~ b;

(Ь> 0),

можем записать

Предположив, что А

= А

= А; получим

ρ _ А _ А ^^ /43 23)

(р+пЬГ~ е

р (l+xb)*'

Рассмотрим три частных случая:

дырочный полупроводник

= ^>0; (43.24)

рР

электронный полупроводник

(43

25)

собственный полупроводник

р==п

х=1

. п

А'1и» (43.26)

ρ л, * I, e

pl+b•

266

Обычно b > 1, поэтому в собственном полупроводнике R 0.

Если 6=1, то

и Е

= 0

—

это соответствует ТОМУ, ЧТО откло-

няемые в одну и ту же сторону электроны и дырка не создают поля

Холла

—

их заряды компенсируют друг друга и поле не возникает.

Если же Ь Φ 0, то R Φ 0, и знак R определяется знаком носителей

заряда, имеющих большую подвижность.

Так как и η и ρ являются функциями температуры, то R также

зависит от температуры. В области собственной проводимости х=1,

R является отрицательной величиной, уменьшающейся по модулю

с ростом Τ. Если при малом Τ полупроводник был акцепторным,

то при этих температурах /?> 0 и, следовательно, с ростом Τ коэф-

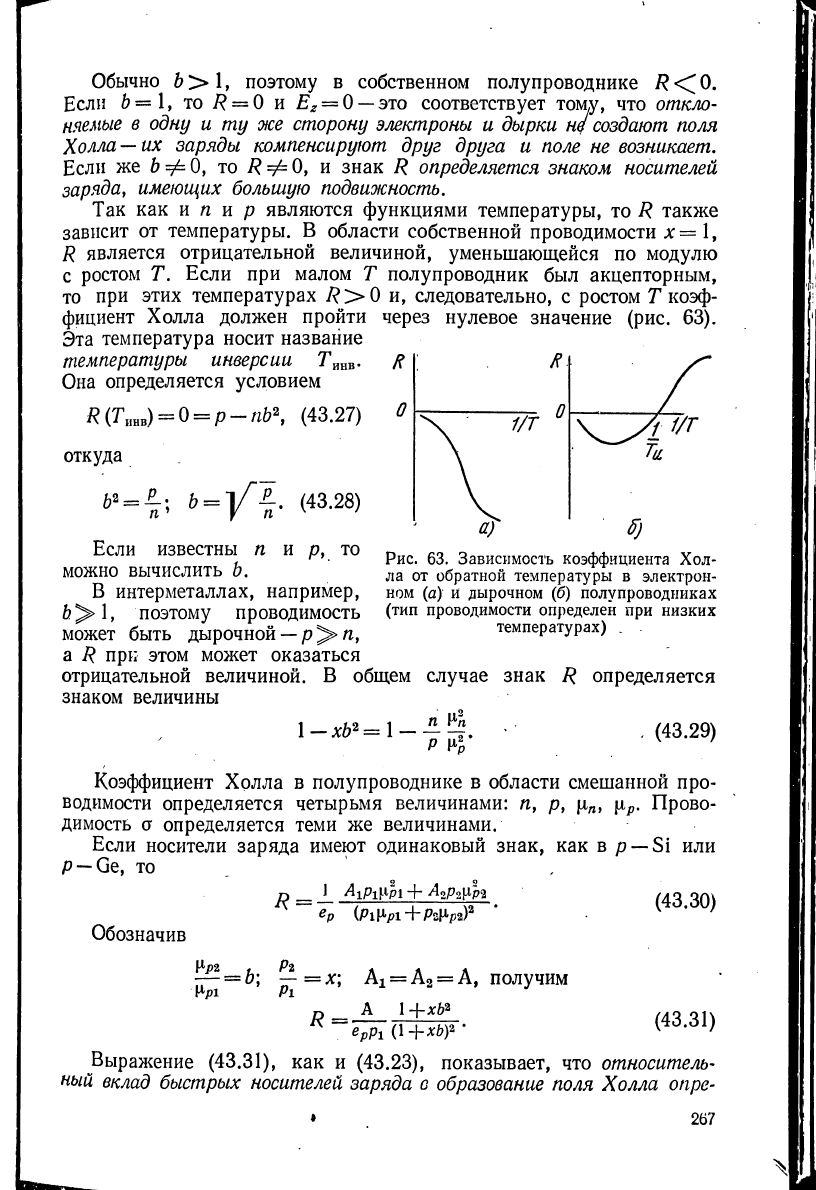
фициент Холла должен пройти через нулевое значение (рис. 63).

Эта температура носит название

температуры инверсии R

Она определяется условием

R{T^) = 0 = p-nb\ (43.27) 0

откуда

= L·. b = V 2-.

η' ψ η

(43.28)

η и ρ, то

Если известны

можно вычислить Ь.

В интерметаллах, например,

, поэтому проводимость

может быть дырочной

—

ρ я,

a R при этом может оказаться

отрицательной величиной. В общем

знаком величины

1 —

xb^

—

Рис. 63. Зависимость коэффициента Хол-

ла от обратной температуры в электрон-

ном (а) и дырочном (б) полупроводниках

(тип проводимости определен при низких

температурах) _

случае

пЙ

ρ μΓ

знак R определяется

. (43.29)

Коэффициент Холла в полупроводнике в области смешанной про-

водимости определяется четырьмя величинами: η, ρ, μ

, μ

. Прово-

димость σ определяется теми же величинами.

Если носители заряда имеют одинаковый знак, как в р

—

Si или

р —Ge, то

R =

—

+ /43

3Q4

ер

(Ριμρΐ

Ρΐ,μρζ)

' \ · )

Обозначив

μρι

Р2

—

Ь\

— =х\ А

= А

= А, получим

A l+xb*

Выражение (43.31), как и (43.23), показывает, что относитель-

ный вклад быстрых носителей заряда в образование поля Холла опре-

267

деляется величиной xb

, в то время как их вклад в проводимость

определяется величиной хЪ, т. е. в эффекте Холла носители заряда

с большей подвижностью играют большую роль, чем в проводимости.

2. Сильные поля. Перейдем к рассмотрению сильных полей:

μα^

^!; из (43.15) можно записать

R =

(43.32)

Для собственного полупроводника числитель (43.32) обращается

в нуль, в то время как знаменатель отличен от нуля при любом

конечном В, поэтому для

собственного

полупроводника

R —

ТК

—

1р

й=

Нг4-

Г"

1 /

—

гр

Зр,

-6п-

/ Ζ 3 4 S 6'7 8 3

/Ъ1/К'

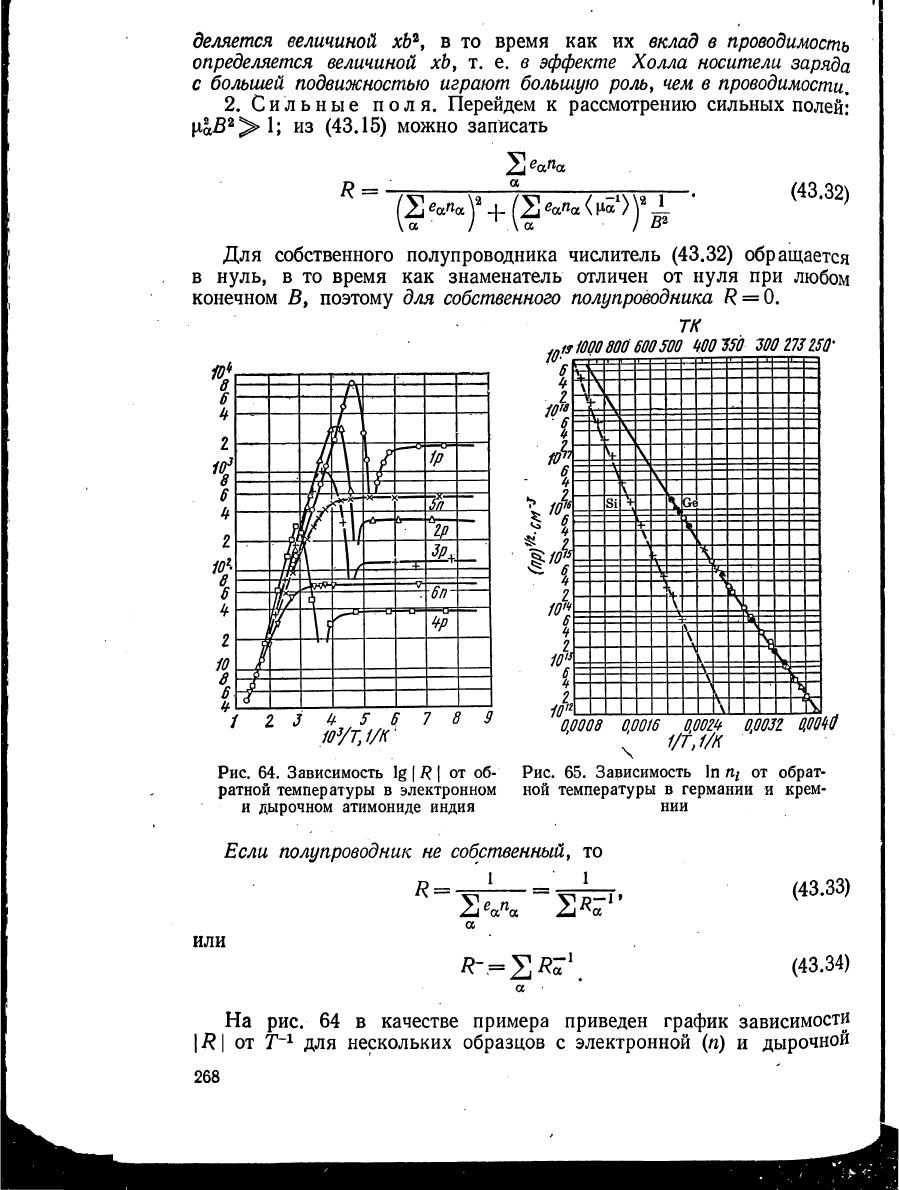
Рис. 64. Зависимость lg

от об-

ратной температуры в электронном

и дырочном атимониде индия

10-

10"

да

Z7\

да ж

•so

f ·

Ш 11 \73

10-

10"

10-

10"

—V

tJ"

- %

\>о)

9 %

« |

^ ί

№

-4

tJ"

- %

\>о)

9 %

« |

^ ί

№

-v

tJ"

- %

\>о)

9 %

« |

^ ί

№

tJ"

- %

\>о)

9 %

« |

^ ί

№

tJ"

- %

\>о)

9 %

« |

^ ί

№

tJ"

- %

\>о)

9 %

« |

^ ί

№

fcr

tJ"

- %

\>о)

9 %

« |

^ ί

№

•J

tJ"

- %

\>о)

9 %

« |

^ ί

№

•J

tJ"

- %

\>о)

9 %

« |

^ ί

№

tJ"

- %

\>о)

9 %

« |

^ ί

№

tJ"

- %

\>о)

9 %

« |

^ ί

№

v—

tJ"

- %

\>о)

9 %

« |

^ ί

№

\ """"

Рис. 65. Зависимость In щ от обрат-

ной температуры в германии и крем-

нии

Если полупроводник не собственный, то

ι 1

R-

или

R~ ==

(43.33)

(43.34)

На рис. 64 в качестве примера приведен график зависимости

\R\ от Т'

для нескольких образцов с электронной (η) и дырочной

268

(ρ) проводимостью. Из рис. 64 видно, что в области низких темпе-

ратур (

от

120° К до 200° К) концентрации носителей заряда остается

постоянной, это соответствует области истощения примеси. Концен-

трация свободных носителей заряда равна 3· 10

смг

в 1р и 1,5 χ

χΙΟ

см~

в 4р. Температура инверсии имеет тем больйшю вели-

чину,

чем

больше концентрация примеси, как это видно из^кривых

для образцов

р, 2р, 3ρ и 4р. Переход к собственной проводимости

происходит при температуре тем меньшей, чем меньше концентра-

ция примеси. В области собственной проводимости lg

меняется

линейно с обратной температурой. На рис. 65 приведен график

зависимости щ в германии и кремнии от обратной температуры,

полученный на основе изучения зависимости коэффициента Холла

от обратной температуры.

§ 44. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА ХОЛЛА

ОТ МАГНИТНОГО ПОЛЯ

Коэффициент Холла, вводимый в выражение для Е

, как пока-

зывает расчет на основе кинетического уравнения, зависит слож-

ным образом от магнитного поля. Соотношения (42.28), (42.41)

и (43.19), (43.33) дают по существу выражения для R, справедливые

лишь в пределах В 0 и В оо , эти предельные выражения обозна-

чим через Rq и /?оо. Рассмотрим теперь выражения, справедливые

при В Φ 0 и В Φ оо . Остановимся вначале на примесном полупро-

воднике с носителями заряда одного типа, для которого R согласно

(42.23) равен

/ μ

D 1 \ l+μ

/ /

44П

-en /

у /

μ2

у ·

(44 Л}

Рассмотрим вначале

вырожденный полупроводник. Согласно

(39.32) усреднение по энергии равносильно подстановке значений

соответствующих величин на поверхности Ферми. В таком случае

(44.1) примет вид:

(Ρ)

ι+μ

(^) в*

/л л ο\

"" en ' . μ

(F) μ

(F)

"" en '

+μ2

(F)

Βψ

+μ2

(F)

Βψ

т. е. для вырожденного полупроводника коэффициент Холла не зависит

от индукции магнитного поля во всем возможном интервале значений.

Рассмотрим теперь невырожденный полупроводник, разложим

величину ^J— в ряд по μ

Г+W = Σ{-1)"(μ*Β*Τ=1-μ*Β* + μ*Β*-μ·Β* + ... (44.3)

269

и в случае слабого поля

ограничимся двумя первыми членами.

Ошибка при этом не будет превосходить μ

. В таком случае

WjW / =

№ ~

№+·

· ·>

~ <^

> -

в2

(трг)=<μ

+· · ·) ~

<μ>

<μ

> я

Из (44.3) и (44.4) получим

1. <μ

)-(μ

> β

(44.4)

R =

en [(μ) — (μ

) Βψ +

[<μ«)

—

<μ«)

Βψ Β

en (μ)

(Ά

Ημ

(μ

) , (μ

)

<μ> ,"

"' <μ>

(44.5)

Так как

ι (μ

en <μ)

RO, то

- R = R

= R

{\-B*(-

<μ

)

-2 <μ> (μ

)

<μ>

+-Ш·

(44

т. е. с ростом поля коэффициент Холла уменьшается пропор-

ционально В

. Коэффициент пропорциональности зависит от

квадрата подвижности и механизма рассеяния. Действительно, обоз-

начим

(μ

)

<μ>

<τ)2 ' /иЛ

<ЧУ>

—

<·ιι^ ν

*·')

<μ>« <*>«

<μ)

(

)

тогда

RB = RO {l - μ|5

(Α

- 2C + -ξ-)}.

(44.8)

Найдем величину коэффициентов А, С и D, когда действует один

механизм рассеяния

—

τ = τ

r(I^Hf)

-2

(л·-гс+ψ)-

['Μ

И1+')1'И1

[

(i+

")[

(l-)T

(44.9)

В табл. 11 приведены значения множителя (44.9) для трех слу-

чаев: р = —

; Р = 0 и р =

270