Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


458
CHAPTER
9.
STOCHASTIC MODELING
When
N
tends toward
infinity,
it is
also possible
to
show
(e.g.,
[84])
that
M£
N
and
YZ
N
tend toward
the
mean
and the
variance
of
Z,
respectively:
For
any
pair
of
RV's
X and
Y",
the
"experimental
covariance"
C\y
N
is
also
defined
as
As
with
the
properties
of the
experimental variance,
it can be
shown
that
Construction
of a
random
sampling
of
13
=
[0,1]
One of the
many
different
procedures traditionally used
in
computer science
for
generating
a
random sampling
of
15
=
[0,1]
is
presented
in
this section.
For
this
purpose, recall
first
that,
on a
32-bit computer,
the
maximum positive
integer
that
one can
represent
is
equal
to
M
=
(2
31
—
1) and
then consider
the
following
Probabilized
Spaces:
13
(15,
A,
IP)
and
(0*,,4*,7P*)
U
=
[0,1]
U*
=
{u*
e
JN+
:
u*
<
M}
A =
Lebesgue
<r-algebra
A* =
cr-algebra
of the
parts
of
15*
]P(A}
=
\A\/\15\
VAeA
JP*(A*)
=
\A*\/\V*\
V
A*
e
A*
(9.30)
For
each
w*
e
15*,
let
15(a;*)
=
{tt>i(u;*),..
.,a;jv(k>*)}
be the
series consisting
of
N
real numbers,
defined
as
follows,
14
on
O
=
[0,1]:
It can be
shown
that
the
series
15(a;*)
so
defined
has a
period equal
to
15
(M
—
l)/2 and,
as
long
as N is
lower
than
this
period, experimental
tests
have shown
that,
for any
segment
Ac
[0,1]
1.
the
number
of
points
Ui(u)*)
belonging
to A is
proportional
to the
length
of
A,
that
is to
say,
to
JP(A),
and
2.
the
number
of
points
uJi(ui*)
belonging
to A has no
influence
on the
possibility
that
U>J(LL)*)
may
also
belong
to A.
In
other words,
15(u*)
honors conditions similar
to
conditions
(9.26)
and,
as
a
consequence,
can be
considered
as a
random sample
of 0 =
[0,1].
13
The
notation
IV
+
represents
the set of the
positive integers.
14
In
this
definition,
the
"modulo" operator
% is
such
that
(a%6)
represents
the
rest
of
the
division
of a by b.
15
For
a 32
bits computer,
this
period
is
equal
to
1,073,741,823,
which
is far
beyond
practical requirements (see
[84]).

9.3.
RANDOM FUNCTIONS
Constructio n
of a
random
sampling
of an RV
Let us now
consider
the
Random Variable
U(uj}
denned
as
follows
on the
Probabilized Space
(£5,
.4,
IP],
itself
denned
according
to
equations (9.30):
According
to
equations
(9.30),
it can be
observed
that
U is
uniformly
dis-
tributed
on the
segment
13
=
[0,1]:
As
a
consequence, according
to the
score-transform theorem,
it is
possible
to
generate
a
random sampling
of any
Random Variable
Z
having
a
given
cdf
FZ
as
follows:
Fundamental
hypothesis:
Random
sampling
For
practical reasons, only
one set
0(u;*)
is
generally available. Consequently,
all
that
has
been said
up to now in
section
(9.2.7)
is
only
a
theoretical
frame-
work:
in
practical applications,
it is
necessary
to use a
fundamental hypothesis
that
assumes
that
the
only available sampling
U(o;*)
of
13
is, in
fact,
a
random
sampling.
Therefore,
throughout
the
remainder
of
this book,
for
simplicity's sake,
the
event
u;*
will systematically
be
omitted
in the
notations. Moreover,
it
will
be
implicitly assumed
that
the
events
are
"well enough" distributed
on
15
for it to be
said
that
• the set
{u>i,..
.,UN}
is a
random
TV-sampling
of
O,
and
• the set
{Z(uji),...,
Z(U>N)}
is a
random
TV-sampling
of
Z.
9.3
Random Functions
9.3.1
Definitions
Let
£ be a
normed
linear vector space (see
[141])
associated with
a
norm noted
as • |
assumed
to
define
the
distance between points
of 8:
=
distance
between
Ui
and
112
Let
us
consider
a
family
Z =
{Z
u
: u
e
D}
composed
of
RV's indexed
by
a
variable
u
with values
in a
region
D of 8. In
practical
applications,
8 is
often
a
"parametric" non-Euclidean curved space having
a finite
dimension
p
generally
equal
to 1, 2, or 3:
• if D is a
part
of a
curve (e.g.,
a
well-path),
then
p = 1;
459

460
CHAPTER
9.
STOCHASTIC MODELING
•
if
D is a
part
of a
curved surface
(e.g.,
a
horizon), then
p = 2; and
• if D is a
part
of a
solid (e.g.,
a
layer), then
p = 3.
If
all of the
RV's
in the
family
Z —
{Z\\
:
u 6
D}
are
defined
on the
same
Probabilized Space
(0,^4,
JP),
then this
family
is
called
a
Random Function
(RF).
From
a
practical point
of
view,
the
three
following
different
notations
for
the
same
RF Z are
used:
It may be
considered
that
•
Z\i(u)
is an RV
generated
by
Z(u,o>)
at
point
u G D.
•
Z
u
(u)
is a
function
of u
generated
by
Z(u,u>)
at
elementary event
u;
e
15.
The
most simple example
of an RF is the
notion
of
Indicator Random Function
Z
u
=
IA(U)
associated with
an
event
A(u)
of A and
which
can be
written
as
The
following
property
is
always
verified
for any
indicator
RF
/A(U)
:
Within
the
framework
of
this chapter,
the
following
notation
will
be
used
for
any
region
D of
8:
In the
case where
D is a finite
set,
as
usual,
\D\
will
represent
the
number
of
elements
of
D.
9.3.2
Moments
of a
Random Function
By
definition,
any RF
Z(u,
u;)
can be
considered either
as a
function
of u or
a
function
of
u;.
These
two
points
of
view
are
associated with
two
families
of
characteristics called "moments"
•
"statistical
moments," also called "moments" when
there
is no
possible
am-
biguity,
are
ordinary functions
denned
by
integrals
on the
variable
u;,
and
•
"spatial
moments"
are
RV's
or
RF's
denned
by
integrals
on the
spatial
variable
u.
Statistical
moments
of an RF
The
mean value
m^(u),
the
covariance
function
CZ(VLI,
u
2
),
the
variance
func-
tion
cr|(u),
and the
variogram
16
7z(ui,
112)
of an RF Z
=
Z(u,
a;),
when they
16
In
the
early
days
of
geostatistics,
the
function
7z(
u
ii
U
2)
was
called
a
"semivariogram."
Nowadays,
the
prefix
"semi"
is no
longer
used.

9.3.
RANDOM FUNCTIONS
exist,
are
ordinary
functions,
as
defined
by
By
definition,
Most
of the
time,
for
simplicity's sake
and
when
there
is no
possible confusion,
the
following
notations
will
also
be
used:
Note
that
the
existence
of
(7(111,112)
implies
the
existence
of
7(111,112),
but
the
reverse
is
false:
C
exists
7
exists
There
is a
family
of
RF's
called "stationary"
RF's
that
are of
particular
in-
terest
in
practical applications; this notion
of
stationarity
[62, 156, 157]
is
defined
as
follows:
When
Z —
Z(u,cu)
is
order
2
stationary, then
it is
easily
verifiable
that
its
variogram
7(11,
u + h)
exists,
is
also stationary,
and is
such
that
Spatial
moments
of an RF
Any
RF is a
function
of two
variables,
uo
and u, and
some (statistical) moments
relative
to the
variable
LU
were presented
in the
section above. Similarly,
it is
possible
to
define
moments relative
to the
variable
u,
called "spatial
moment:"
•
where they exist,
the
spatial mean value
m
s
(u>)
and the
spatial
variance
cr
s2
(o;)
of an RF
Z(u,uj)
are
ordinary RV's defined
as
461

462
CHAPTER
9.
STOCHASTIC MODELING
•
where they exist,
the
spatial covariance
C
s
(h,
u>)
and the
spatial
vari-
ogram
7
s
(h,
u;)
of an RF are
RF's,
as
defined
by
Ergodicity
From
a
practical point
of
view,
to
make computing possible,
it is
almost always
necessary
to use a
"magic" property
specific
to
RF's called
ergodicity.
This
amounts
to
assuming
that
statistical
moments
and
spatial moments
can be
identified:
• An RF Z is
said
to be
order
1
ergodic
if it is
already order
1
stationary
and if,
when
\D\
tends toward
infinity
in
equation
(9.34),
the
following
property
holds true
for the
mean value
of Z:
• An RF Z is
said
to be
order
2
ergodic
if it is
already order
2
station-
ary and if,
when
|D(h)|
tends toward
infinity
in
equation
(9.35),
the
following
property holds true
for the
covariance
of Z
or,
similarly,
if:
Note
that
the
above definitions
of
ergodicity
can be
slightly weakened
in the
following
sense:
• An RF Z is
said
to be
order
1
weakly ergodic
if it is
already
order
1
stationary
and if,
when
D\
tends toward
infinity
in
equation
(9.34),
the
following
property holds true
for the
mean value
of Z:
• An RF Z is
said
to be
order
2
weakly ergodic
if it is
already order
2
stationary
and if,
when
|Z?(h)|
tends toward
infinity
in
equation
(9.35),
the
following
property holds true
for the
covariance
of Z
or,
similarly,
if

9.3.
RANDOM FUNCTIONS
Ergodicity viewed
as a
model
For
practical reasons,
in
Computer-Aided design,
one
traditionally
chooses
to use
spline
functions,
for
example,
to
model
parametric curves
and
sur-
faces.
This does
not
means
that
all the
parametric curves
and
surfaces
in the
universe
are
spline
functions.
This simply means
that
parametric curves
and
surfaces
can be
fairly
well
approximated
by
spline
functions,
which,
in
turn,
can be
efficiently
implemented
in
computerized models.
Similarly,
in
practical applications,
one
traditionally
chooses
to use er-
godic
RF's
to
model
the
behavior
of
stochastic phenomena. This does
not
mean
that
all
stochastic phenomena
in the
universe
are
ergodic. This simply
mean
that
ergodic models
can
fairly
well
approximate
the
behavior
of
stochas-
tic
phenomena and,
in
addition, allow mean
and
covariance
functions
to be
estimated
from
partial observations
of
these phenomena.
9.3.3
Modeling
C(ui,
u
2
)
Posit
ivity
Let
us
consider
a
finite
set
D*
consisting
of N
sampling points
that
belong
to
the
parametric domain
D:
For any
such sampling, there
is an
associated vectorial
RV Z
deduced
from
the RF
Zu(w)
=
Z(u,aj)
in
such
a way
that
This implies
that
the
associated covariance matrix
[C
zz
]
is
such
that
It has
been shown (see equation
(9.19))
that
any
covariance matrix must
be
semipositive
definite
and
this must
be
true
for the
above matrix
whatever
the
number
N of
sampling points
{iij}.
This suggests
the
following
definition:
A
function
C(ui,u
2
)
will
be
said
to be
"semipositive
definite"
if,
and
only
if,
any
matrix
[C
zz
]
deduced
from
(7(111,112)
according
to the
above schema
is
semipositive
definite.
This
definition
characterizes
the
covariance
functions
and it
will
be
said
that
A
function
G(UI,
u
2
)
is a
covariance
function
if, and
only
if,
it is
semipositive
definite.
463

464
CHAPTER
9.
STOCHASTIC MODELING
Bochner's
famous
theorem [62, 159] characterizes
the
family
of
stationary
covariance
functions:
Any
continuous
stationary
covariance function
C(h)
is
propor-
tional
to the
Fourier
Transform
of
a
symmetrical
pdf
/(s):
In
the
above expression,
(s-h)
represents
the
scalar product
of
vectors
s and h
of
the
^-dimensional
parametric space
E
=
1R
P
,
while
i is the
pure imaginary
number equal
to
\/—T.
In
practical applications, this theorem
is
extremely
useful
for
building models
of
covariance
functions
that
fit the
observed
data.
One-dimensional
covariance
functions
If
p = 1,
then, using
the
Bochner theorem,
it can be
shown
that
the
following
functions
are
proportional
to the
Fourier transform
of
symmetrical pdf:
•
Gaussian
model
•
Exponential
model
•
Spherical
model
•
Nugget-effect
model
Note
that
the
above covariance models
are
normalized
in
such
a way
that
(7(h)
~
0 as
soon
as h
>
1.
^-dimensional
covariance
functions
Let
us
consider
the
quadratic
form
D
2
(h)
as
defined
by
where
[R
2
]
is a
given symmetrical positive
definite
matrix called
the
"range
matrix."
Let
1Z(R
2
)
be the
associated
set of
vectors
of
7R
P
,
as
defined
by
In the
M
p
parametric space,
7i(R
2
}
is an
ellipsoid called
the
"range ellipsoid"
such
that

9.3.
RANDOM FUNCTIONS
It can be
observed
that
the
one-dimensional covariance
functions
cov\(s)
de-
nned
in the
previous section
are
such
that
This suggests
the
following
definition
of the
^-dimensional
covariance
functions
for
all h
belonging
to £
=
JR
P
:
According
to
equations
(9.44)
and
(9.45),
it can be
concluded
that
the
range
ellipsoid
split
the
M
p
parametric space
in two
regions such
that
figure
(9.5) shows
an
example
of
such
an
ellipsoid
in a
curved
3-dimensional
parametric space
8
=
1R
consisting
of a
stratigraphic grid:
due to the
curva-
ture
of the
stratigraphic grid
and the
faults,
when observed
from
the
(x,
y,
z]-
embedding
Euclidean space,
the
ellipsoid appears
deformed
and
cut.
Nested
covariance
functions
Let
us
consider
a
series
of
independent,
centered random
functions
and let
Z(u,
u;)
be the
associated random
function,
as
denned
by
Noting
the
covariance
function
of
Z(u,
uS)
as
C(h)
and the
covariance
function
of
Zi(u,uj)
as
Ci(h),
it is
easy
to
check
that
In
other words,
the sum of
several covariance
functions
is
still
a
valid
co-
variance
function.
The
resulting composite covariance
is
called
a
"nested"
covariance
function.
Such
a
decomposition provides great
flexibility
when modeling covariance
functions
from
experimental
data:
equation
(9.47)
can be
considered
as a
polynomial whose terms have
to be
adjusted
to fit an
experimental covariance
function.
By
convention,
the first
component
of the
above decomposition
(9.47)
is
identified
to the
nugget
effect,
if
any:
•
Co(h)
is
assumed
to be a
pure
nugget
effect,
and
•
Ci(h)
is
assumed
to
hold
no
nugget
effect
for any i > 0.
The
next section shows
how
C*(h),
or
equivalently 7(h),
can be fit to
experi-
mental values computed
from
the
observed
data.
465
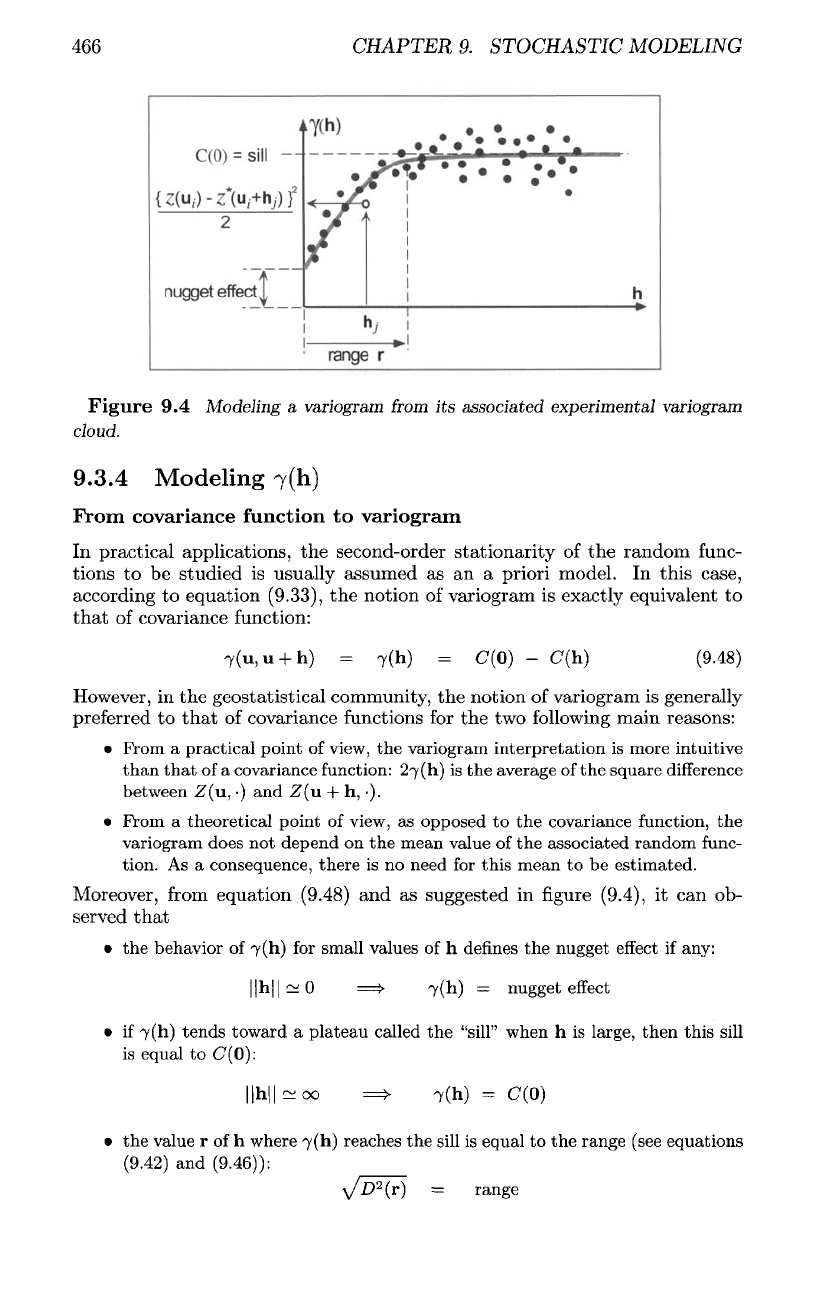
466
CHAPTER
9.
STOCHASTIC
MODELING
Figure
9.4
Modeling
a
variogram
from
its
associated experimental variogram
cloud.
9.3.4
Modeling
7(h)
From
covariance
function
to
variogram
In
practical
applications,
the
second-order
stationarity
of the
random
func-
tions
to be
studied
is
usually
assumed
as an a
priori
model.
In
this
case,
according
to
equation
(9.33),
the
notion
of
variogram
is
exactly
equivalent
to
that
of
covariance
function:
However,
in the
geostatistical
community,
the
notion
of
variogram
is
generally
preferred
to
that
of
covariance
functions
for the two
following
main
reasons:
•
From
a
practical point
of
view,
the
variogram interpretation
is
more intuitive
than
that
of a
covariance
function:
27(h)
is the
average
of the
square
difference
between
Z(u,
•) and
Z(u
+ h, •).
•
From
a
theoretical
point
of
view,
as
opposed
to the
covariance function,
the
variogram does
not
depend
on the
mean value
of the
associated random
func-
tion.
As a
consequence, there
is no
need
for
this mean
to be
estimated.
Moreover,
from
equation
(9.48)
and as
suggested
in
figure (9.4),
it can ob-
served
that
• the
behavior
of
7(h)
for
small values
of h
defines
the
nugget
effect
if
any:
• if
7(h) tends toward
a
plateau called
the
"sill" when
h is
large, then this sill
is
equal
to
C*(0):
• the
value
r of h
where 7(h) reaches
the
sill
is
equal
to the
range (see
equations
(9.42)
and
(9.46)):

9.3.
RANDOM FUNCTIONS
Estimatin g
a
variogram:
one-dimensional
case
In
practice,
it is
possible
to
estimate
the
variogram
of a
random
function
Z(u,
(jj)
under
the two
following
(sufficient
but not
necessary) conditions:
•
Z(u,cj)
is a
second-order
stationary
ergodic
RF, and
•
Z(ui,uj)
=
z(ui)
is
known
on a finite set D* =
{ui,..
.,UAT}
of
data
points
belonging
to the
domain
of
definition
D.
In
this
case, equation (9.38)
can be
numerically
approximated
17
by a
finite
sum
with
the
following
form
where
D*(h)
represents
the
subset
of D*
consisting
of
points
u^
such
that
(ui
+h)
belongs
to
D*.
However,
there
is a
major drawback
in
this equation:
if
the
data
points
are
sampled randomly
in D,
then there
are few
chances
for
(ui
+ h) to
belong
to D* and
z(\ii
+ h) is
then unknown. Several practical
strategies
have been implemented
to
overcome this
difficulty
[111,
58,
224];
the
simplest
is to
replace
z(iij
+ h) by the
value
z*(\ii
+h),
defined
as
follows,
where
u^
1
is the
closest point
to
(u^
+ h) in
D*:
As
suggested
in figure
(9.4),
if 8 is a
1-dimensional
parametric space,
the
variogram cloud
is
defined
as the set of
points
{hj,
\z(ui]
—
z*(\ii
+
h-,)|
2
/2}
and the
"experimental" variogram
has an
equation chosen
to fit as
much
as
possible this
set of
points.
Estimating
a
variogram:
p-dimensional
case
Most
of the
time,
in the
geosciences,
3-dimensional
variograms
are
used and,
as
suggested
in figure
(9.5),
it is
common practice
to
proceed
as
follows:
•
Build
the
one-dimensional
variogram
clouds
associated
with
a
series
of
given
predefined
directions
in
]R
3
.
•
Choose
a
3-dimensional
variogram
model
and
adjust
interactively
its
range
and
nugget
effect,
if
any,
to fit, in a
least
square
sense,
the
one-dimensional
clouds
in all of the
predefined
directions.
For
example,
figure
(9.5) shows
the
control panel corresponding
to the
"var-
iogram analyzer" proposed
by
GQCAD
for
estimating
a
3-dimensional vari-
ogram
in the
parametric curvilinear space corresponding
to a
stratigraphic
grid.
17
This
estimation
is
biased
if the
points
Uj
are
clustered
and it may be
necessary
to
use
a
"declustering"
technique (see
[168]).
Nevertheless
in
practice, this approximation
is
generally
considered
acceptable
for
small
h.
467
