Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

This page intentionally left blank

GEOMODELING

This page intentionally left blank

Chapter
Discrete Modeling
for
Natural Objects
This
introductory chapter presents
a
discrete
approach
specially designed
for
modeling
the
geometry
and the
properties
of
natural objects such
as
those
encountered
in
biology
and
geology.
Contrary
to
classical
Computer-Aided
Design
methods
based
on
continuous
(polynomial)
functions,
the
proposed
approach
is
based
on a
discretization
of the
objects close
to the finite
ele-
ment
techniques
used
for
solving partial
differential
equations. Each object
is
modeled
as a set of
interconnected nodes having both
the
geometry
and
the
physical properties
of
the
objects,
and the
Discrete Smooth Interpolation
method
is
used
for fitting the
geometry
and the
properties
to
complex data.
Each
datum
is
turned
into
a
linear constraint
and
some constraints related
to
typical
information encountered
in
numerical geology
are
presented.
1.1
Introduction
In
this introduction,
we
would like
to
emphasize
the
need
for a new
breed
of
Computer-Aided
Design (CAD) specially dedicated
to the
modeling
of
natu-
ral
objects such
as
those encountered
in
biology
and
geology.
In a
nutshell,
we
could
say
that
a
user
of a
traditional
CAD
software creates nice curves,
surfaces
and
volumes without
any
constraint, while
a
user
of a CAD
software
dedicated
to the
modeling
of
natural objects
has to
respect constraints
in-
duced
by the
observed
data.
All of
these traditional
CAD
software
programs
are
based
on
parametric
methods
such
as
those
introduced
by
Bezier
in the
early 1970s.
The
goal
of the
mathematicians
who
designed these methods
(e.g.,
Barnhill
1
1

CHAPTER
1.
DISCRETE
MODELING
FOR
NATURAL OBJECTS
Figure
1.1 An
example
of
complex data
to
take
into
account when modeling
geological
horizon.
(Data
courtesy
of
Unocal)
[13];
Bezier
[27];
de
Boor
[54,
55];
Farin
[77];
...)
was
simply
to
propose
tools
for
modeling
nice
curves
and
surfaces
interactively
and not to
respect
complex
data
such
as
those
encountered
in
geology.
For
example,
if we
consider
the
geological
horizon
(=surface)
shown
in
figure
(1.1),
we can say
that
the
data
available
are
complex
for the
following
reasons:
• The
data
are
heterogeneous
because
we
have
to
account
simultaneously
for:
—
the
locations
of the
intersections
of the
well-curves with
the
surface
to
be
modeled (see pages
184 and
263),
—
the
slope
of the
tangent plane
to the
surface when this slope
has
been
measured
at the
intersections
of the
wells with
the
surface (see page
267),
—
seismic
data
corresponding
to
cross sections
of the
surface
(see page
264),
—
structural information consisting
of 3D
fault-throw vectors (see page
273),
—
geometric information
specifying
that
the
surface should respect
a
given
partial
differential
equation (see page
267),
and
—
physical
properties
(seismic velocities,
reflectivities,...)
attached
to the
surface
and
observed directly
or
indirectly
at
some locations (see page
256).
2

1.1.
INTRODUCTION
• The
data
are
more
or
less reliable;
for
example,
well
data
are
more reli-
able
than
seismic
data,
which
in
turn
are
more reliable than structural
data.
• The
data
are
irregularly distributed
and are
generally strongly clustered
on
lines
and
surfaces.
In
practice, this clustering generates numerical
instabilities
in
most
of the
numerical methods used
for
interpolating
the
data.
Another major drawback with traditional
CAD
methods
is
that
they
are de-
signed
for
modeling
the
geometry
of
objects
and not to
take into account
the
physical properties
attached
to
these objects.
In
geology, there
is a
strong
need
to
model
the
geometry
and the
properties simultaneously since there
are
many cases where they
are
linked:
for
example,
the
geometry
and the
seismic
velocity
of
geological layers
are
interdependent.
Mathematical methods used
in
traditional
CAD
have
not
been designed
for
addressing such complex
data
and it is too
optimistic
to
think
that
these
methods could
be
adapted
to
account
for all of the
data
available,
while
re-
specting their complexity
[148].
In
fact,
these methods were initially designed
for
the
needs
of the car
industry [27]
and we are in
search
of a
specific
class
of
mathematical modeling methods specially designed
to
meet
the
needs
of the
geosciences.
The
success
of
polynomial models used
in
traditional
CAD
[166] comes
from
the
fact
that
polynomials generate aesthetic curves
and
surfaces
and
this
is of
paramount importance
in the car
industry
[27].
However,
in the
geosciences,
our
primary concern
is
more
to
respect
the
constraints induced
by
the
data
than
to
produce nice-looking objects.
It is
generally admitted
that
discretized problems
are
simpler
to
solve
than
those based
on
continuous
representations
and
this
is
why,
in
this chapter,
we
propose
to
abandon
the
polynomial
models used
in
traditional
CAD in
favor
of a
discrete approach
close
to the
"finite
elements" technique used
for
solving partial
differential
equations.
Despite
the
fact
that
they
are
less
well
known than parametric methods,
discrete modeling methods have been formulated
and
implemented
in
varying
ways
for
over seventy years. Examples include: Whittaker
[232];
Horton
[107];
Bergthorsson
and
Doos
[21];
Weaver
[227];
Arthur
[9];
Harder
and
Desmarais
[102];
Briggs
[34];
Akima
[4];
Sibson
[202];
Mallet [147, 149,
150];
Overveld
[170].
The
goal
of
this chapter
is to
propose
a
generic
formulation
of
discrete
modeling
which generalizes most
of
these methods.
The
approach presented
in
this chapter
was
specially designed
for
model-
ing
natural objects
and is
potentially able
to
account
for any
series
of
(linear)
constraints corresponding
to the
influence
of the
data
on the
model. Each
of
these constraints
can be
weighted
by a
"certainty factor" used
for
specifying
its
importance relative
to the
other constraints.
This
is
particularly interest-
ing
in the
geosciences
where,
due to
sampling errors,
it may
happen
that
some
constraints become contradictory.
For
example,
if the
projection
of two
seis-
mic
cross sections
in the
(x,
y)
horizontal plane meet
at
some point
P(x,
y),
it
3
4
CHAPTER
1.
DISCRETE MODELING
FOR
NATURAL OBJECTS
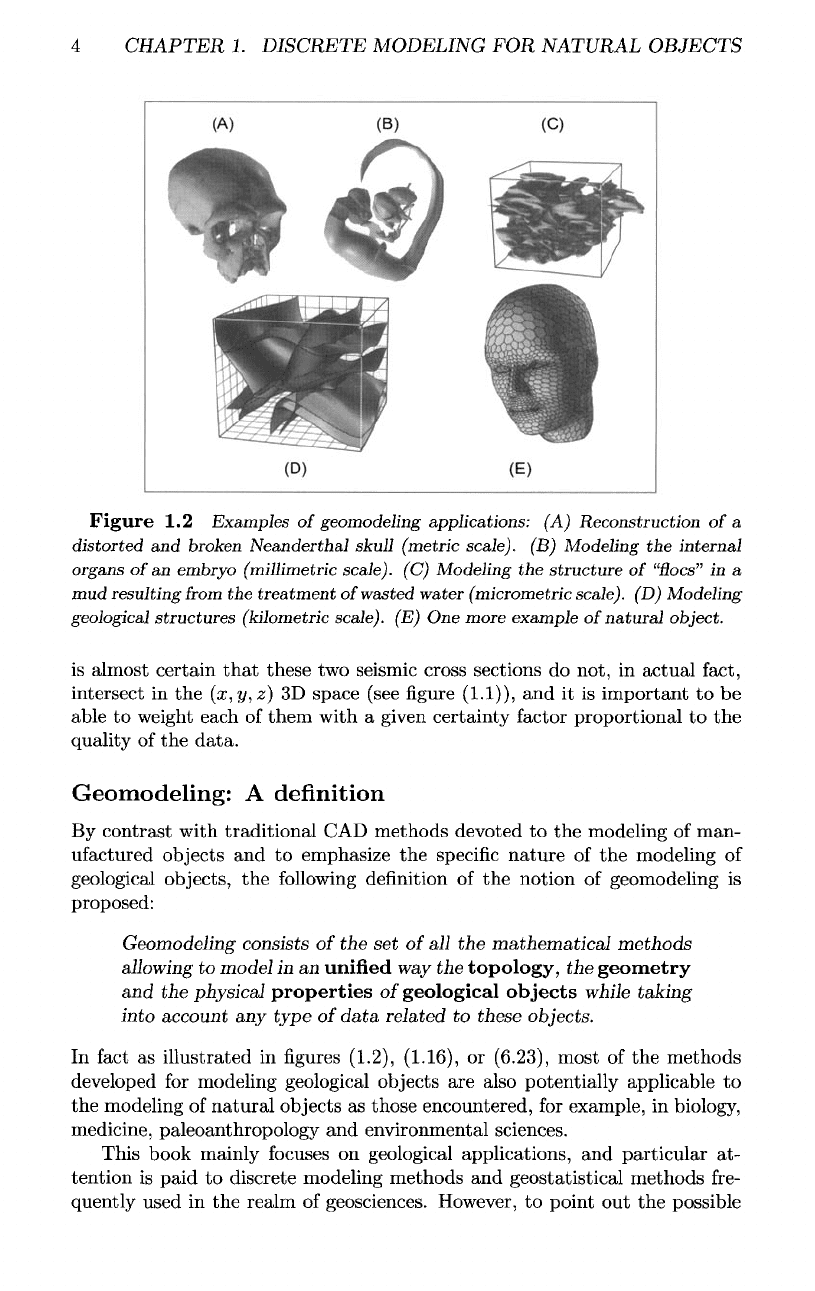
Figure
1.2
Examples
of
geomodeling
applications:
(A)
Reconstruction
of a
distorted
and
broken
Neanderthal
skull
(metric
scale).
(B)
Modeling
the
internal
organs
of an
embryo
(millimetre
scale).
(C)
Modeling
the
structure
of
"Hoes"
in a
mud
resulting
from
the
treatment
of
wasted
water
(micrometric
scale).
(D)
Modeling
geological
structures
(kilometric
scale).
(E) One
more
example
of
natural
object.
is
almost certain
that
these
two
seismic cross sections
do
not,
in
actual
fact,
intersect
in the
(x,y,z)
3D
space (see
figure
(1.1)),
and it is
important
to be
able
to
weight each
of
them with
a
given certainty factor proportional
to the
quality
of the
data.
Geomodeling:
A
definition
By
contrast with traditional
CAD
methods devoted
to the
modeling
of
man-
ufactured
objects
and to
emphasize
the
specific
nature
of the
modeling
of
geological
objects,
the
following
definition
of the
notion
of
geomodeling
is
proposed:
Geomodeling
consists
of the set of all the
mathematical methods
allowing
to
model
in an
unified
way the
topology,
the
geometry
and
the
physical
properties
of
geological
objects
while taking
into
account
any
type
of
data related
to
these objects.
In
fact
as
illustrated
in figures
(1.2),
(1.16),
or
(6.23),
most
of the
methods
developed
for
modeling geological objects
are
also potentially applicable
to
the
modeling
of
natural objects
as
those encountered,
for
example,
in
biology,
medicine,
paleoanthropology
and
environmental sciences.
This
book mainly
focuses
on
geological applications,
and
particular
at-
tention
is
paid
to
discrete modeling methods
and
geostatistical methods fre-
quently
used
in the
realm
of
geosciences. However,
to
point
out the
possible

1.2.
DISCRETE MODELING
Figure
1.3
Neighborhood
N(a}
of
node
a is
composed
of
a
plus
all
nodes
of
its
orbit
N°(a)
=
{0i,02,
• •
•}•
This
figure
corresponds
to the
special case where
N(o)
is
denned
as the set
of
nodes
that
can be
reached
in at
most
s(a)
=
I
step from
the
node
a.
use of
these methods
in
other
fields of
science,
a few
non-geological examples
of
applications
will also
be
given.
1.2
Discrete modeling
This
section
presents
in a
general
and
abstract
way the
notion
of a
discrete
model,
which
can be
used
for
approximating complex natural objects encoun-
tered,
for
example,
in the
geosciences.
Discrete topological model
£7(f2,
N)
As
shown
in figures
(1.3)
and
(1.5),
the
main idea
of a
discrete model
is
that
the
topology
of any
object
can be
approximated
by a
graph
^(0,
N)
where:
• 0 is the set of all the
nodes
of the
graph, each
of
these nodes being
identified
with
its
rank order:
5
N is an application from into a subset of such that
can be reached in at most steps from
CHAPTER
1.
DISCRETE MODELING
FOR
NATURAL OBJECTS
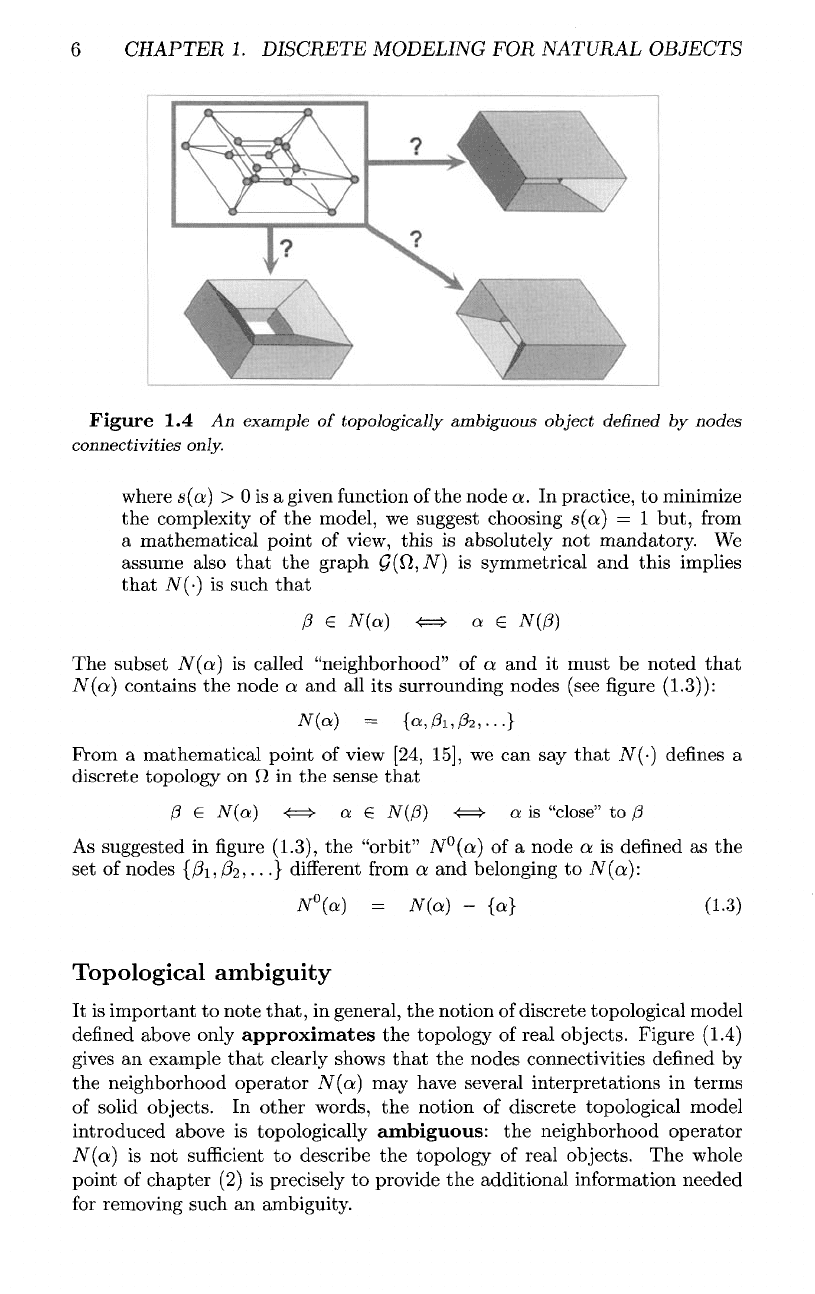
Figure
1.4 An
example
of
topologically
ambiguous
object
defined
by
nodes
connectivities
only.
where
s(a]
> 0 is a
given
function
of the
node
a. In
practice,
to
minimize
the
complexity
of the
model,
we
suggest choosing
s(a)
=
I
but,
from
a
mathematical
point
of
view,
this
is
absolutely
not
mandatory.
We
assume also
that
the
graph
£(Q,/V)
is
symmetrical
and
this implies
that
N(-)
is
such
that
0
e
N(a)
a £
JV(0)
The
subset
N(a)
is
called "neighborhood"
of a and it
must
be
noted
that
TV
(a)
contains
the
node
a and all its
surrounding nodes (see
figure
(1.3)):
N(a)
=
{a,
ft,
&,...}
From
a
mathematical point
of
view
[24, 15],
we can say
that
N(-)
defines
a
discrete
topology
on
Jl
in the
sense
that
As
suggested
in figure
(1.3),
the
"orbit"
7V°(a:)
of a
node
a is
defined
as the
set of
nodes
{/?i,
02>
• • •}
different
from
a and
belonging
to
N(a}:
Topological ambiguity
It is
important
to
note
that,
in
general,
the
notion
of
discrete topological model
defined
above only
approximates
the
topology
of
real objects. Figure (1.4)
gives
an
example
that
clearly shows
that
the
nodes connectivities
defined
by
the
neighborhood operator
N(a)
may
have several interpretations
in
terms
of
solid objects.
In
other words,
the
notion
of
discrete topological model
introduced
above
is
topologically
ambiguous:
the
neighborhood operator
N(a)
is not
sufficient
to
describe
the
topology
of
real objects.
The
whole
point
of
chapter
(2) is
precisely
to
provide
the
additional information needed
for
removing such
an
ambiguity.

1.2.
DISCRETE MODELING
Figure
1.5
Examples
of
objects
approximated
by
discrete
model:
(A)
Faulted
triangulated
geological
surface.
(B) Set of
adjacent
tetrahedra
filling a
geological
layer.
(C)
Polygonal
curves.
(D)
Faulted
curvilinear
grid
filling a
geological
layer.
Examples
of
discrete
topological
models
Potentially,
the
notion
of
discrete topological model presented
in the
previous
section
can be
used
for
approximating
the
topology
of any
geological object.
For
example
and as
suggested
in
figure
(1.5),
it is
possible
to
model:
• a
geological horizon
or a
fault
(surface)
as a set of
adjacent triangles
(figure
(1.5)-A),
• a
geological body (solid)
as a set of
adjacent
tetrahedra
(figure
(1.5)-B),
• a
geological cross section
(curve)
as a set of
adjacent segments
(figure
(1.5)-C),
and
• a
geological layer (solid)
as a
regular curvilinear
or
rectilinear grid (fig-
ures (1.5)-D
and
(1.6)-B).
In
these models,
the
vertices
of the
triangles, tetrahedra,
and
segments corre-
spond
to the
nodes
of
&(£l,
N),
while
the
edges
define
(partly)
the
topology.
The
introduction
of a
discontinuity between
two
adjacent nodes
a and (3 is
straightforward,
and,
as
suggested
in figure
(1.6),
this
can be
achieved simply
by
removing
the
edge
(a,
/?)
from
the
network.
Notion
of
discrete model
.M
n
(n,7V,
(p,
C)
The
discrete topological model
£?(i7,
N)
introduced
in the
previous sections
does
not
take into account
the
properties
of the
objects.
As
shown
in figure
(1.7), such properties
are
modeled
as a
series
</?
of n
numerical
functions,
called
components
of
(/?,
defined
on the set of
nodes
O
of
G(£l,
N):
7
