Jean-Laurent Mallet. Geomodeling

18

CHAPTER

1.

DISCRETE MODELING

FOR

NATURAL OBJECTS

Generalization

of the

DSI

method

In

practical applications,

the

function

(p

of the

discrete model

Ai

n

(0,

TV,

<^,

C]

may

have several components interacting through "cross" constraints

(see

page

9).

Thus

the

simplified

version

of the DSI

method presented

in the

previous section

has to be

extended

somewhat

to

take

into

account

the

mul-

ticomponent case where:

The

multicomponent problem

can be

solved with generalized local

DSI

equa-

tions identical

in

form

to the one

obtained

in the

case where

(p

has

only

one

component.

As

will

be

seen

later

on, a

slight change

in the

notations

used

in

the

definition

of the

local roughness criterion

R((f>\a]

together with

the

degree

of

violation

of the

constraints

p(f\c)

suffices:

In

the

above

definition

of the

roughness

R(y>\a),

r

v

is a

given

positive weight-

ing

coefficient

allowing

the

contribution

of the

function

<£>"(•)

to the

local

roughness

R((p\ot)

to be

modulated.

If the

functions

{^{-)}

have approxi-

mately

the

same magnitude,

then

it is

possible,

for

example,

to

choose

all the

coefficients

{r"}

equal

to 1.

The

equation allowing

the

value

(p

v

(oi)

in the

iterative

DSI

algorithm

to

be

updated remains almost unchanged

in its

form

(see

equation

(4.46))

and

becomes:

The

only noticeable

difference

in the

monocomponent case

is a

slight

modifi-

cation

of the

term

T

v

(a\(f>)

in the

case

of

cross constraints involving several

components

of

(p

(see page

163).

When there

is no

such cross constraint

at-

tached

to the

node

a,

then

the

above

formulas

are

absolutely identical

to the

ones

in the

monocomponent case.

Implementation

of the DSI

method

In

spite

of its

apparent complexity,

the

local

DSI

equation

is

very simple

to

program

and the

very heart

of the

iterative algorithm introduced

on

page

17

can be

implemented

in

about

30

lines

of

source code.

The

real programming

difficulty

comes

from

the

discrete model

.A/l

n

(O,

N,

<p,C),

which

has to be

implemented

to

•

optimize

the

access

to the

neighborhoods

N(a)

and the

values

<p"(oi)

used

by

the DSI

equation,

and

•

take

into

account

its

"self-consistency"

when modifications

occur

in

Q,

AT(-),

</?,

or C.

1.4.

EXAMPLES

OF

APPLICATIONS

19

Figure

1.10

Each

point

Pi is

assumed

to

hold

data

4>(Pi)

which

are

projected

onto

the

triangulated

surface

in

direction

A(Pi)

specific

to Pi.

Data

4>(Pi)

are

transformed

into

constraints

affecting

the

nodes

corresponding

to the

vertices

of

the

triangle

hit by

A(Pi).

If

the

direction

A(Pi)

is

changed,

then

a

different

triangle

is

hit and the

constraints

have

to be

updated.

Implementing

a

totally

general algorithm

that

takes

into account

these

two

items

may

result

in a

large complex software with more

than

100

thousand

lines

of

source code playing

the

role

of a

server

for the 30

lines corresponding

to the

DSI

algorithm. Such heavy machinery

is not

always necessary

and its

presentation

is

beyond

the

scope

of

this book.

A

look

at

figure

(1.10) gives

an

idea

of the

nature

of the

problem: this

figure

represents

a

triangulated surface

and a set of

data

points

{Pi,

P

where

each point

Pi is

assumed

to

hold

data

0(P;)

that

are

projected onto

the

triangulated

surface

in a

direction

A(P^)

specific

to Pi. The

data

tf>(Pi) are

transformed

into constraints

affecting

the

nodes corresponding

to the

vertices

of

the

triangle

hit by

A(Pj).

As a

result

of

this

situation:

• If the

direction

A(Pi)

is

changed,

then

a

different

triangle

is hit and the

associated

constraint

c

(E

C has to be

updated.

• If the

density

of the

nodes

in a

region

of the

model

is

changed

to

obtain

a

better

numerical

approximation,

then

the set fi and the

neighborhoods

{N(a)

:

a G

Q}

are

changed

and it is

necessary

to

update

all the

constraints

c

G

C in

order

to

take into account these global

modifications.

The

implementation

may be

even more complex

if, at

each

DSI

iteration,

the

direction

of

projection

A(Pj)

is

optimized automatically

to hit the

closest

point

of the

surface.

1.4

Examples

of

applications

Applications

of

discrete models

and

Discrete Smooth Interpolation introduced

in

this chapter

are

numerous,

and the

choice

of a

specific

example

is

difficult.

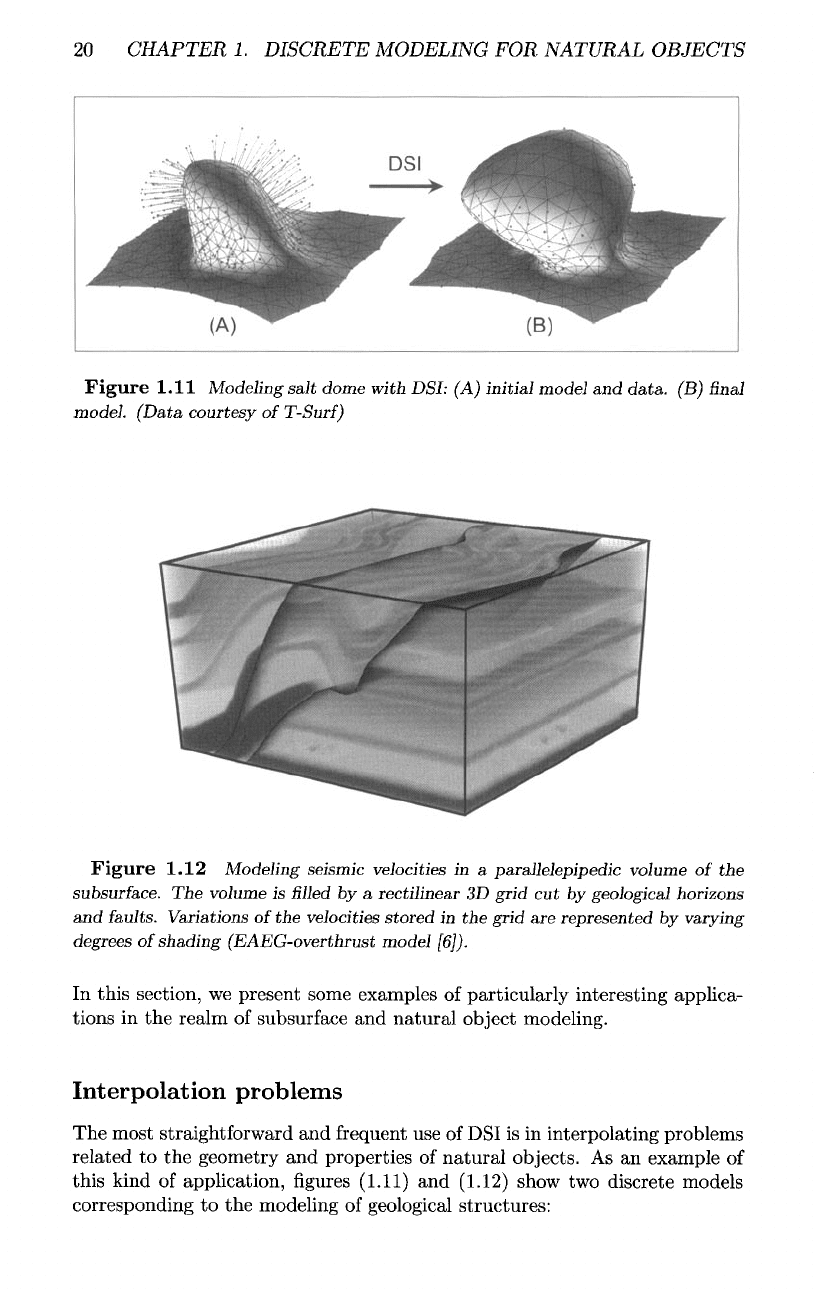
20

CHAPTER

1.

DISCRETE MODELING

FOR

NATURAL OBJECTS

Figure

1.11

Modeling salt dome

with

DSI:

(A)

initial model

and

data.

(B) final

model. (Data courtesy

of

T-Surf)

Figure

1.12

Modeling seismic velocities

in a

parallelepipedic volume

of the

subsurface.

The

volume

is filled by a

rectilinear

3D

grid

cut by

geological horizons

and

faults. Variations

of

the

velocities stored

in the

grid

are

represented

by

varying

degrees

of

shading (EAEG-overthrust model

[6]).

In

this section,

we

present some examples

of

particularly interesting applica-

tions

in the

realm

of

subsurface

and

natural object modeling.

Interpolation problems

The

most straightforward

and

frequent

use of DSI is in

interpolating problems

geometry

and

properties

of

natural objects.

As an

example

of

this kind

of

application,

figures

(1.11)

and

(1.12) show

two

discrete models

corresponding

to the

modeling

of

geological structures:

1.4.

EXAMPLES

OF

APPLICATIONS

The first

example presented

in figure

(1.11)

is

modeling

of

the

geometry

of a

salt

dome.

In figure

(l.ll)-A,

there

are

about

100

data

points

Pi,

which

are

assumed

to be

located

on the

surface

to be

constructed.

As

suggested

in figure

(1.10), each

of

these

data

points

is

projected onto

the

surface according

to a

specific

direction

A(P;),

hitting

a

triangle

Ti(ctQ,

&i,

a

2

]

at a

point

P*.

It is

possible

to

define

a

linear constraint

c —

c(i)

on the

nodes

(ao,

&i,

&%),

specifying

that

Pi

should

be

coincident with

P*.

The

modeling process

is

split into three

steps:

1.

First,

an

initial

discrete

model

.A/f

n

(f2,

JV,

<£,

C),

consisting

of a

rectan-

gular

triangulated

surface,

is

created

in the

neighborhood

of the

data

points

{Pi}.

2.

Each

data

point

Pi is

projected

onto

the

closest point

of

this initial

surface

and is

transformed into

a

constraint

c —

c(i)

G C

applied

to the

components

(<p

x

,

ip

y

,

<f>

z

)

that

corresponds

to the

location

of the

nodes

of

the

surface.

3.

The

DSI

algorithm

is

applied.

After

convergence

if

necessary,

to

give

more flexibility

to the

surface,

the

triangles with

the

distance

d(Pi,P*)

bigger

than

a

given threshold

can be

split

before returning

to

item

(2)

above. Moreover,

as

suggested

in figure

(1.10), between

two

iterations

of

the DSI

algorithm,

it is

also possible

to

optimize

the

directions

of

projection

A(Pj).

After

some iterations

of

this modeling process,

we

obtain

the

model

represented

in figure

(l.ll)-B.

The

second example presented

in figure

(1.12)

corresponds

to the

mod-

eling

of a

seismic velocity

in a

parallelepipedic

volume

of the

subsurface.

This volume

is filled by a

regular rectilinear

3D

grid having

200

steps

in

the

^-direction,

200

steps

in the

y-direction

and 100

steps

in the z-

direction. This grid

is

assumed

to be cut by

some horizons

and

listric

faults

and the

velocities

(j)

v

(Pi}

are

known

at

about

150

points

{Pi}

irregularly distributed

in the

volume. Each

data

point

{Pi,(j)

v

(Pi}}

is

transformed

into

a

constraint

specifying

that

the

velocity

(f>

v

(a,o)

of the

closest node

ao

should

be

equal

to the

given value

0

v

(Pj).

The

varia-

tions

of the

velocities, restricted

to one

layer,

are

shaded

on the

faces

of

the

parallelepipedic volume shown

in figure

(1.12).

As you can

see,

all

the

discontinuities corresponding

to the

intersections

of the

grid with

the

horizons

and

faults

have been strictly honored.

However,

it

should

be

noted

that,

if

necessary, partial continuity

can be

maintained across

these surfaces

by

keeping

a few

connections

at

random between nodes

located

on

both sides;

in

this case,

the

density

of the

connections

to be

retained could

be

modeled

as a

property

of the

surfaces.

The

third example presented

in figure

(1.13)

is a

very simple tutorial

example showing

the

behavior

of the DSI

interpolation when modeling

a

closed polygonal curve controlled

by

four

Control-Nodes displayed

as

small cubes.

It can be

shown

that

the

resulting discrete curve

fits a

perfect

circle

if the two

following

conditions

are

respected:

21

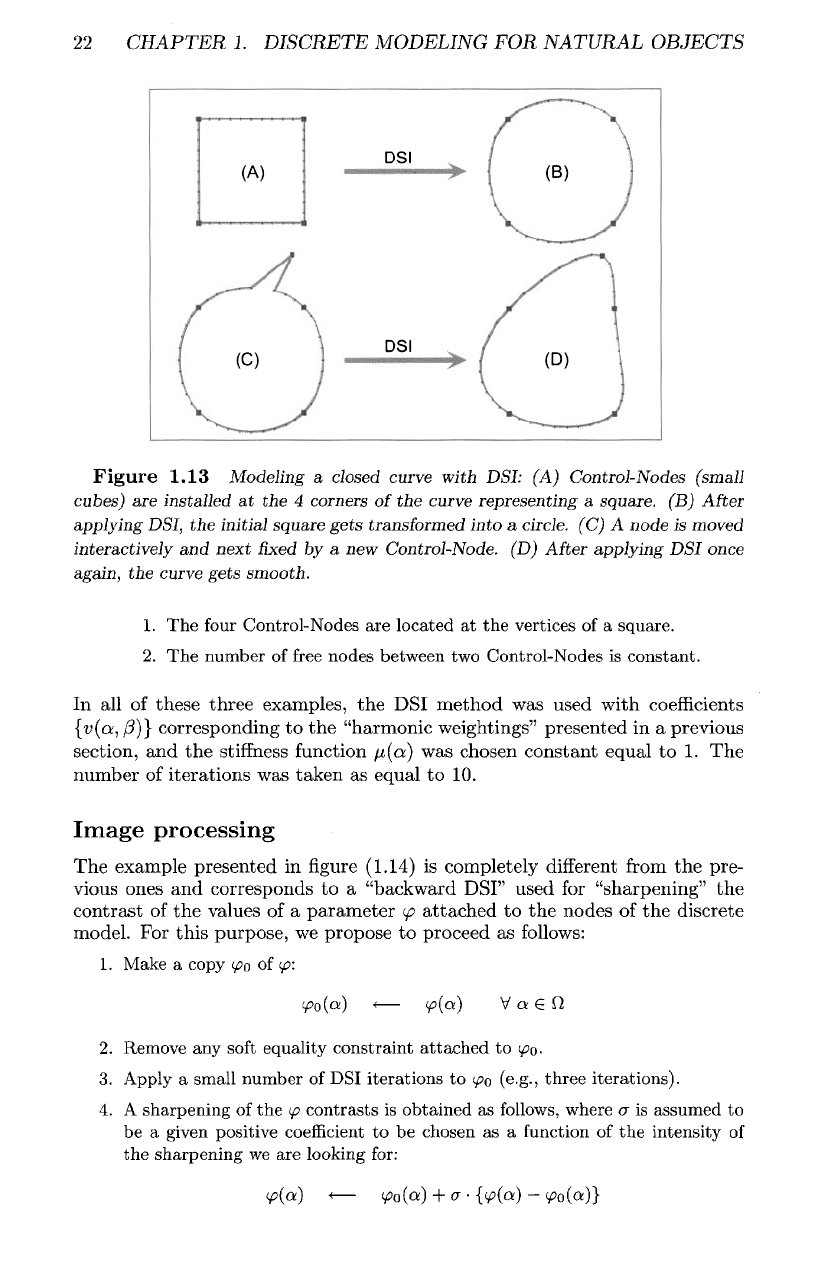
22

CHAPTER

1.

DISCRETE MODELING

FOR

NATURAL

OBJECTS

Figure

1.13

Modeling

a

closed

curve

with

DSL (A)

Control-Nodes

(small

cubes)

are

installed

at the 4

corners

of the

curve representing

a

square.

(B)

After

applying

DSI,

the

initial square gets

transformed

into

a

circle.

(C) A

node

is

moved

interactively

and

Control-Node.

(D)

After

applying

DSI

once

again,

the

curve gets

smooth.

1.

The

four

Control-Nodes

are

located

at the

vertices

of a

square.

2.

The

number

of

free

nodes between

two

Control-Nodes

is

constant.

In all of

these three examples,

the DSI

method

was

used with

coefficients

{v(a,

j3}}

corresponding

to the

"harmonic weightings" presented

in a

and the

stiffness function

//(a)

was

chosen constant equal

to 1. The

number

of

iterations

was

taken

as

equal

to 10.

Image processing

The

example presented

in

figure

(1.14)

is

completely

different from

the

pre-

vious ones

and

corresponds

to a

"backward DSI" used

for

"sharpening"

the

contrast

of the

values

of a

parameter

<p

attached

to the

nodes

of the

discrete

model.

For

this

purpose,

we

propose

to

proceed

as

follows:

2.

Remove

any

soft

equality constraint attached

to

(/?o-

3.

Apply

a

small number

of DSI

iterations

to

tpo

(e.g.,

three iterations).

4. A

sharpening

of the

(p

contrasts

is

obtained

as

follows,

where

a is

assumed

to

be a

given positive

coefficient

to be

chosen

as a

function

of the

intensity

of

the

sharpening

we are

looking

for:

1.

Make

a

copy

</?o

of

(p:

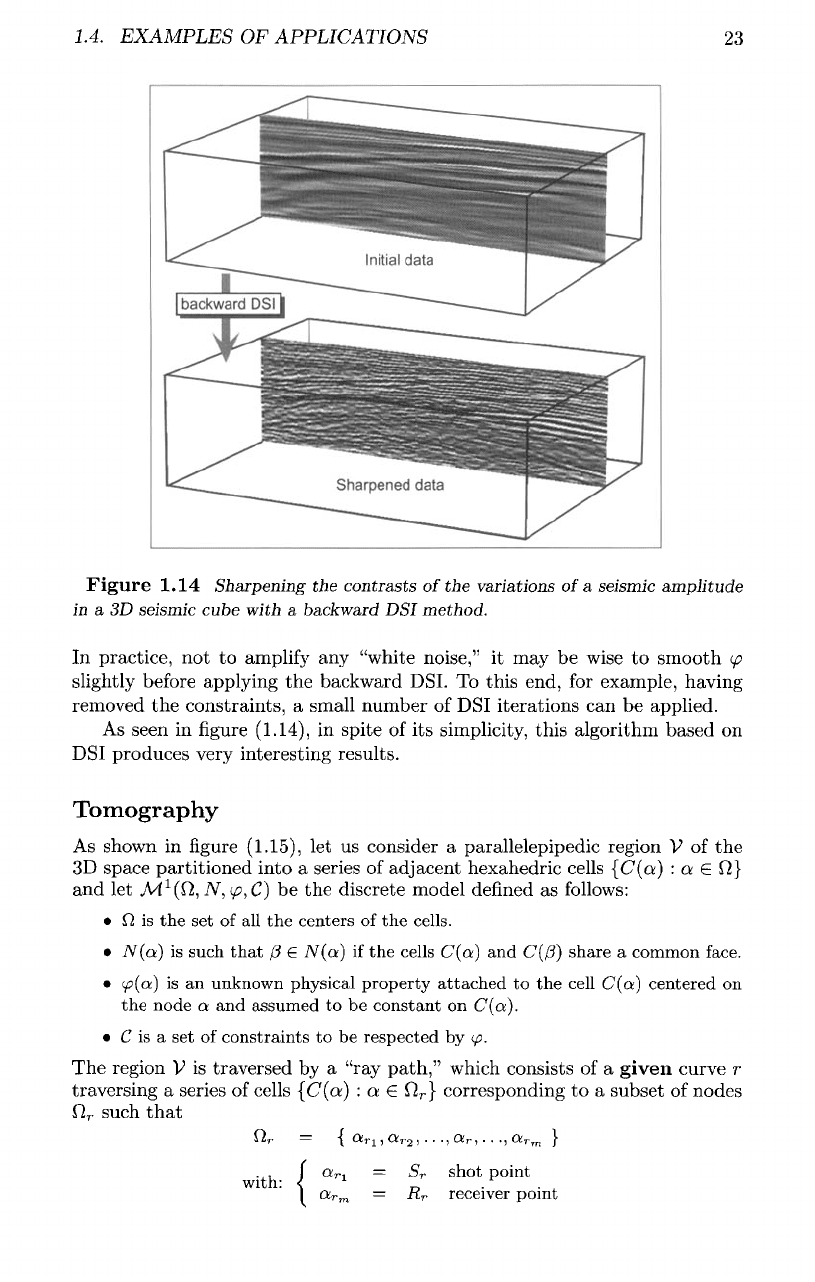
1.4.

EXAMPLES

OF

APPLICATIONS

23

Figure

1.14

Sharpening

the

contrasts

of

the

variations

of

a

seismic

amplitude

in

a 3D

seismic

cube

with

a

backward

DSI

method.

In

practice,

not to

amplify

any

"white noise,"

it may be

wise

to

smooth

(f>

slightly

before

applying

the

backward DSI.

To

this end,

for

example, having

removed

the

constraints,

a

small number

of DSI

iterations

can be

applied.

As

seen

in figure

(1.14),

in

spite

of its

simplicity, this algorithm based

on

DSI

produces very interesting results.

Tomography

As

shown

in figure

(1.15),

let us

consider

a

parallelepipedic region

V of the

3D

space partitioned into

a

series

of

adjacent hexahedric cells

{C(a}

:

a 6

il}

and let

A

/

1

(S7,7V,

</?,C)

be the

discrete model

defined

as

follows:

•

Q

is the set of all the

centers

of the

cells.

•

N(a)

is

such

that

(3

G

N(a)

if the

cells

C(a)

and

C(/3)

share

a

common

face.

•

(p(oi)

is an

unknown

physical

property

attached

to the

cell

C(a)

centered

on

the

node

a and

assumed

to be

constant

on

C(a).

• C is a set of

constraints

to be

respected

by

(p.

The

region

V is

traversed

by a

"ray path,"

which

consists

of a

given

curve

r

traversing

a

series

of

cells

{C(a}

:

a €

Q

r

}

corresponding

to a

subset

of

nodes

O

r

such

that

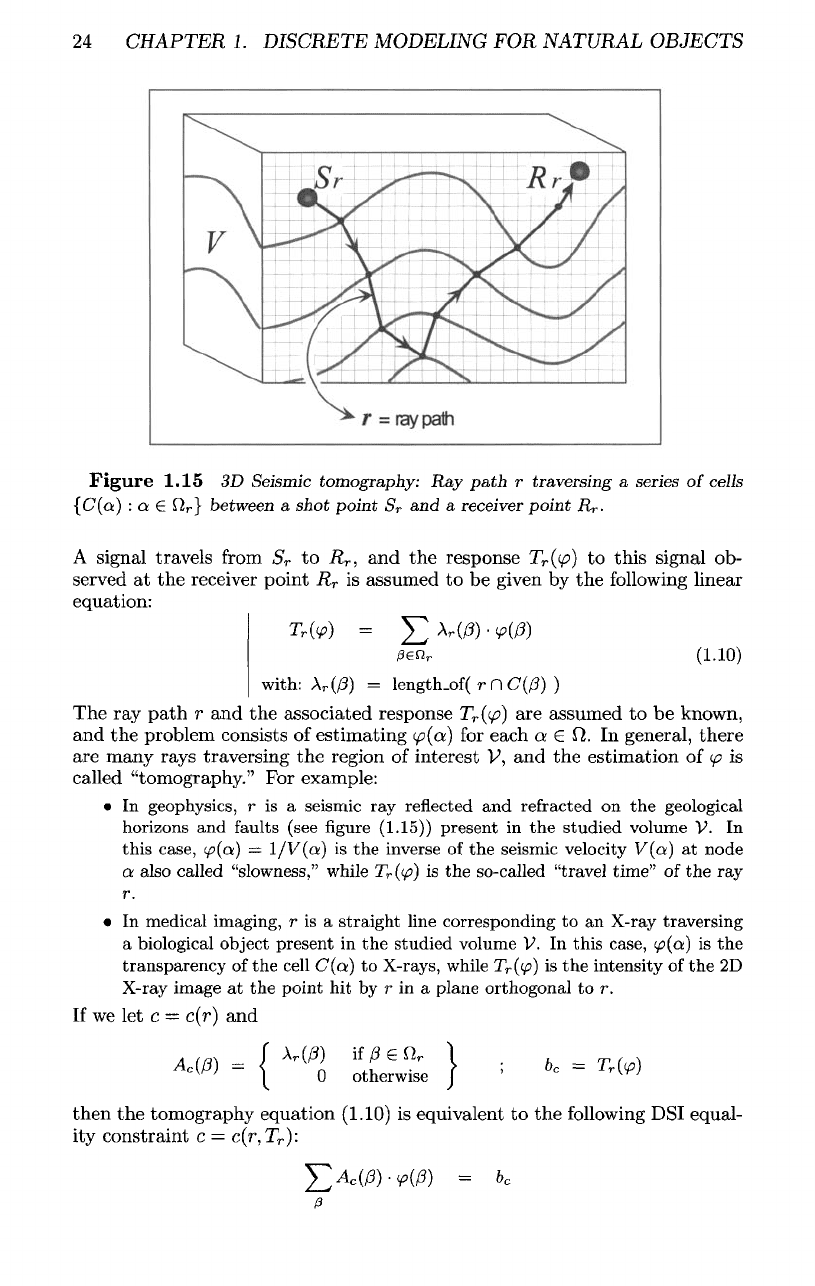
24

CHAPTER

1.

DISCRETE

MODELING

FOR

NATURAL OBJECTS

Figure

1.15

3D

Seismic tomography:

Ray

path

r

traversing

a

series

of

cells

{C(a)

:

a G

O

r

}

between

a

shot point

S

r

and a

receiver

point

R

r

.

A

signal

travels

from

S

r

to

R

r

,

and the

response

T

r

((p)

to

this

signal

ob-

served

at the

receiver

point

R

r

is

assumed

to be

given

by the

following

linear

equation:

The ray

path

r and the

associated

response

T

r

((p)

are

assumed

to be

known,

and the

problem

consists

of

estimating

</?(a)

for

each

a E

£7.

In

general,

there

are

many

rays

traversing

the

region

of

interest

V, and the

estimation

of

(p

is

called

"tomography."

For

example:

• In

geophysics,

r is a

seismic

ray

reflected

and

refracted

on the

geological

horizons

and

faults (see

figure

(1.15))

present

in the

studied volume

V. In

this case,

(p(oi)

—

l/V(a)

is the

inverse

of the

seismic velocity

V(a)

at

node

a

also

called "slowness," while

T

r

(tp)

is the

so-called

"travel time"

of the ray

r.

• In

medical imaging,

r is a

straight line corresponding

to an

X-ray traversing

a

biological object present

in the

studied volume

V. In

this case,

<p(a)

is the

transparency

of the

cell

C(ce)

to

X-rays, while

T

r

(if>)

is the

intensity

of the 2D

X-ray image

at the

point

hit by r in a

plane

orthogonal

to

r.

If

we let c —

c(r]

and

then

the

tomography

equation

(1.10)

is

equivalent

to the

following

DSI

equal-

ity

constraint

c =

c(r,

T

r

):

1.4.

EXAMPLES

OF

APPLICATIONS

25

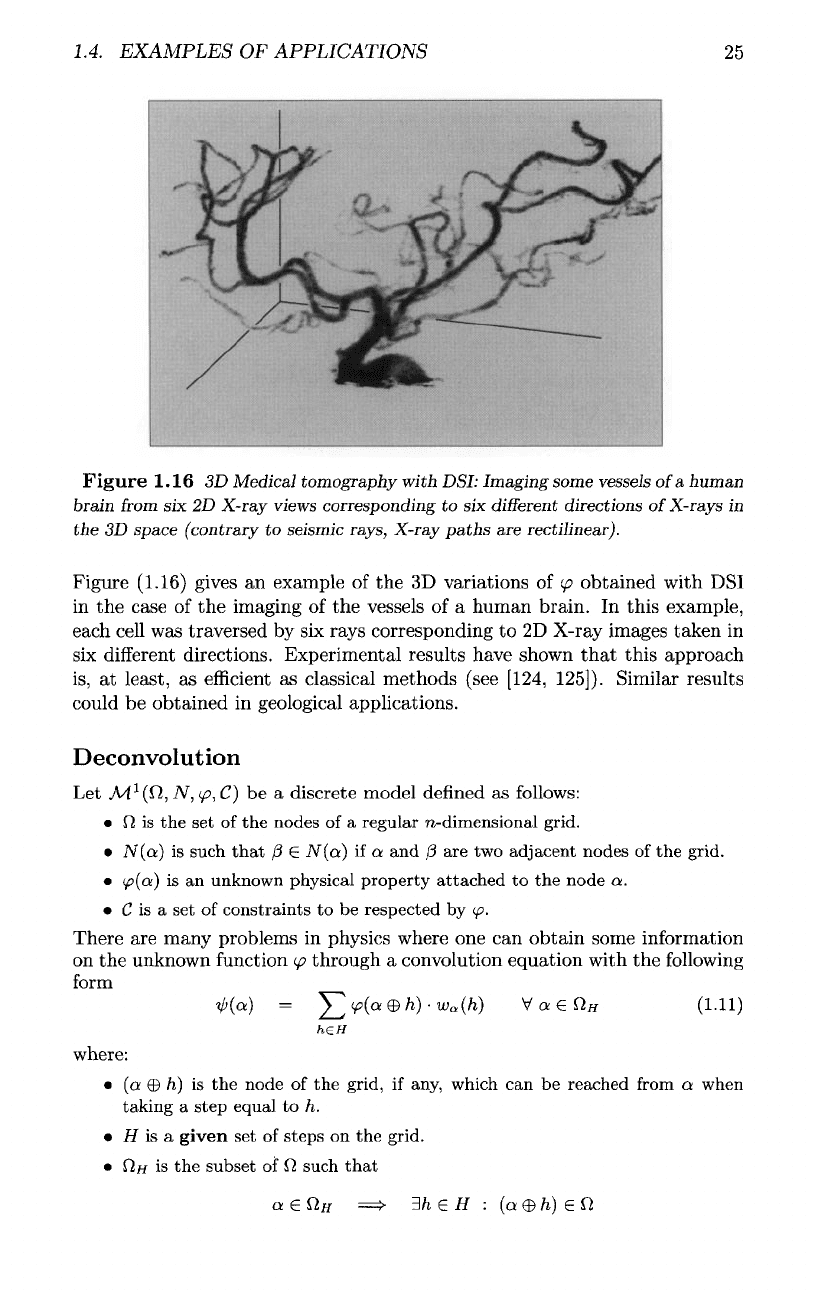
Figure

1.16

3D

Medical tomography

with

DSI:

Imaging some vessels

of

a

human

brain from

six 2D

X-ray views corresponding

to six

different

directions

of

X-rays

in

the 3D

space (contrary

to

seismic rays, X-ray

paths

are

rectilinear).

Figure (1.16) gives

an

example

of the 3D

variations

of

(p

obtained with

DSI

in

the

case

of the

imaging

of the

vessels

of a

human brain.

In

this example,

each

cell

was

traversed

by six

rays corresponding

to 2D

X-ray images taken

in

six

different

directions. Experimental results have shown

that

this approach

is,

at

least,

as

efficient

as

classical methods (see [124,

125]).

Similar results

could

be

obtained

in

geological applications.

Deconvolution

Let

A

/

(

1

(O,

TV,

y?,

C]

be a

discrete

model

defined

as follows:

•

SI

is the set of the

nodes

of a

regular

ra-dimensional

grid.

•

N(a)

is

such

that

/3

€

N(a)

if a and

(3

are two

adjacent

nodes

of the

grid.

•

<p(°i)

i

s

an

unknown physical property

attached

to the

node

a.

• C is a set of

constraints

to be

respected

by

<p.

There

are

many problems

in

physics where

one can

obtain some information

on the

unknown

function

(p

through

a

convolution equation with

the

following

form

where:

(a 0 ft.) is the

node

of the

grid,

if

any, which

can be

reached

from

a

when

taking

a

step

equal

to ft.

H is a

given

set of

steps

on the

grid.

QH

is the

subset

of

SI

such

that

26

CHAPTER

1.

DISCRETE MODELING

FOR

NATURAL OBJECTS

w

a

(h)

is a

given

function

denned

on

H.

It

should

be

noted

that,

if

necessary,

w

a

(h)

can

also

depend

on a

G

fi.

tl>(a)

is a

given

function

defined

on

Q#.

For

each node

a

e

Q#,

we

would

like

to

define

a

DSI

constraint

c =

c(a,

w,

H,

T/J)

on

(p

specifying

that

the

convolution

equation

(1.11)

should

be

respected.

For

this purpose,

let us

define

the

coefficients

A

c

(j3)

and

b

c

as

follows:

It is

easy

to

check

that,

for

each node

a E fi#, we

have:

This

is a

classic linear equality constraint, which

can

easily

be

taken into

account

by

DSI.

Among

the

most traditional applications

of

deconvolution

in

seismic pro-

cessing,

we can

mention

the

reconstitution

of the

seismic

impedance

5

<p(oi)

as

a

function

of the

seismic amplitude

i^(ot)

observed

at the

nodes

of a

regular

3D

grid similar

to the one

shown

in figure

(1.14).

In

this case,

the set H

corresponds

to a

vertical window, while

the

function

w

a

(h)

is a

"wavelet"

corresponding

to the

seismic signal.

1.5

Conclusions

The few

examples presented above represent only

a

very small

part

of the

wide

scope

of

applications

that

can be

addressed using

the DSI

method

in

association with

the

notion

of a

discrete model.

A

large part

of

this book

is

dedicated

to an

extensive presentation

of the

mathematics

and the

appli-

cations

of

DSI.

Before

diving into elaborate mathematical concepts,

the few

examples above have

already

provided

an

understanding

of the

crux

of

this

method.

To sum up, DSI

uses

two

ingredients:

DSI

applies

the old

"divide

and

conquer"

principle:

any

global

complex

problem

is

split

into

a

series

of

small

localized

linear

problems

that

are in

turn

transformed

into

DSI

constraints.

DSI

uses

a

"minimum energy"

principle

to

link,

as

smoothly

as

possible,

the

small

localized

problems:

this

corresponds

to the

minimization

of the DSI

roughness,

whose

only

role

is to

ensure

the

existence

and

uniqueness

of the

solution

(see

section

(4.3)).

The

real secret

of the

efficiency

and the

simplicity

of DSI is to be

found

by

combining

these

two

principles.

5

In

seismic

processing,

"seismic impedance"

is

defined

as the

product

<p(a)

of the

seismic

velocity

V(a)

by the

density

p(a)

of the

subsurface:

Chapter

2

Cellular

Partitions

The

notion

of

discrete model introduced

in the

previous chapter relies strongly

on a

decomposition

of

objects

into

a finite set of

connected nodes. However,

as

pointed

out in figure

(1.4),

such nodes connectivities

are not

sufficient

to

describe

without

ambiguity

the

topology

of

these objects.

In

this

chapter,

we

will

see how

cellular

partitions

can

achieve this goal

in a

completely general

way, whatever the object (manifold/non-manifold) or the dimension of the

embedding space

(ID,

2D,

...,

nD).

2.1

Introduction

It is

well known

that

complex biological objects, also called organs, consist

of

sets

of

adjacent "biological

3D

cells," which

are

structured

to

respect

the

external

and

internal boundaries

of

these objects.

It can be

observed

that

•

from

a

mathematical

point

of

view,

each

3D

cell

is in

fact

an

element

of

volume

which

can be

transformed

into

a 3D

ball,

continuously,

and

•

each

3D

cell

holds

attributes

consisting

of

information

attached,

for

example,

to its

genes.

Similarly,

as

shown

in

figures

(2.1),

(2.35),

(3.17),

and

(3.23),

the

subsur-

face

can be

decomposed into "geological

3D

cells" having attributes (physical

properties)

and

bounded

by

geological horizons

and

faults.

As

suggested

in

figure

(2.2),

the

same approach

can be

used

to

decompose

a

geological cross

section

or a

geological

map

into

2D

cells (which

can be

transformed into

a 2D

ball,

continuously).

Over

the

past

decade,

this

cellular paradigm

has

been used

by

several

computers scientists

as a

template

for

modeling

the

topology

of

complex

ob-

jects (e.g.,

see

[35,

37, 66, 67, 68,

134,

181]).

A

complete presentation

of the

27

Jean-Laurent Mallet. Geomodeling

Подождите немного. Документ загружается.