Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

38
CHAPTER
2.
CELLULAR PARTITIONS
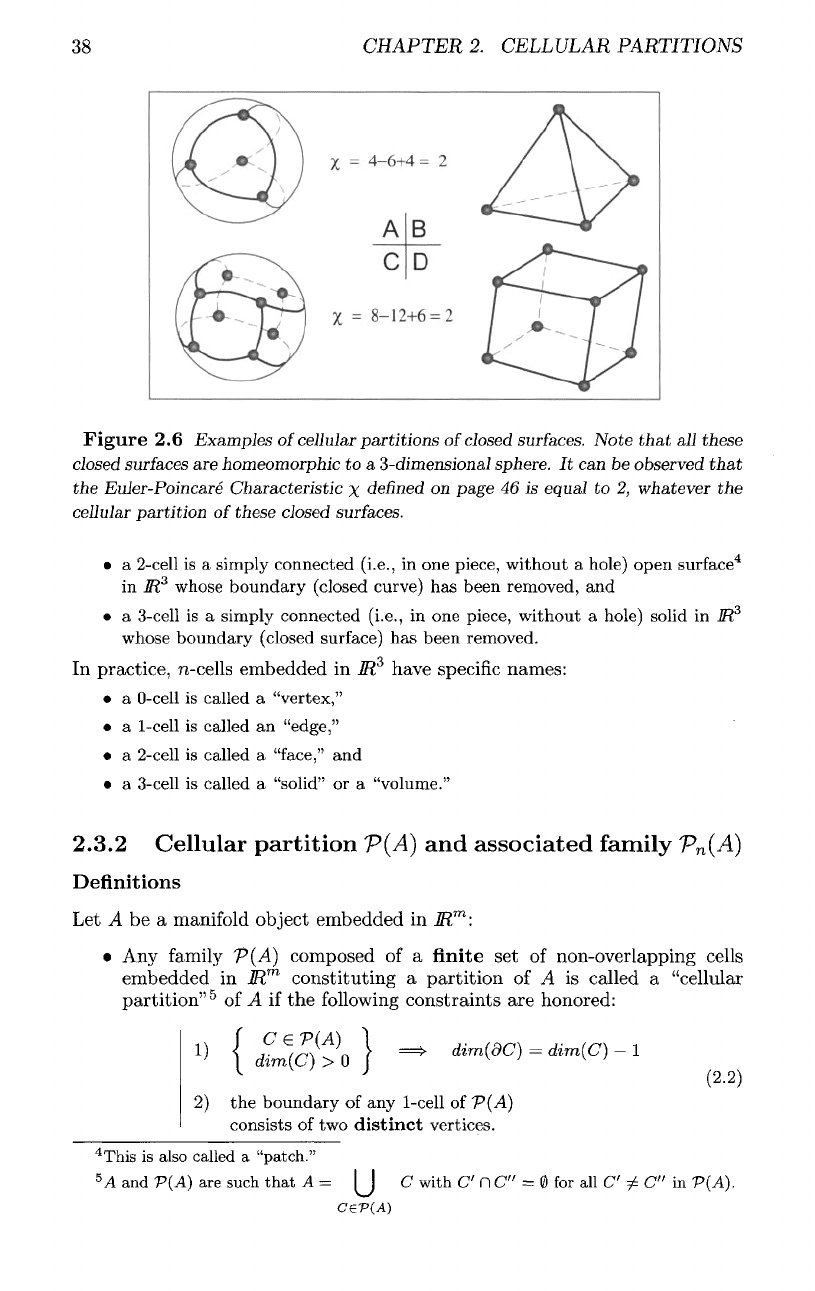
Figure
2.6
Examples
of
cellular
partitions
of
closed
surfaces.
Note
that
all
these
closed
surfaces
are
homeomorphic
to a
3-dimensional
sphere.
It can be
observed
that
the
Euler-Poincare
Characteristic
x
defined
on
page
46 is
equal
to 2,
whatever
the
cellular
partition
of
these
closed
surfaces.
a
2-cell
is a
simply connected
(i.e.,
in one
piece, without
a
hole) open
surface
4
in
IR
3
whose boundary (closed curve)
has
been removed,
and
a
3-cell
is a
simply connected
(i.e.,
in one
piece, without
a
hole) solid
in
JR
3
whose
boundary (closed
surface)
has
been removed.
In
practice,
n-cells
embedded
in
IR
3
have
specific
names:
a
0-cell
is
called
a
"vertex,"
a
1-cell
is
called
an
"edge,"
a
2-cell
is
called
a
"face,"
and
a
3-cell
is
called
a
"solid"
or a
"volume."
2.3.2
Cellular
partition
P(A)
and
associated
family
P
n
(A)
Definitions
Let A be a
manifold
object
embedded
in
7R
m
:
• Any
family
P(A)
composed
of a finite set of
non-overlapping
cells
embedded
in
lR
m
constituting
a
partition
of A is
called
a
"cellular
partition"
5
of A if the
following
constraints
are
honored:
This
is
also
called
a
"patch."
5
A
and
P(A)
are
such
that
A
-.
2)
the
boundary
of any
1-cell
of
P(A]
consists
of two
distinct
vertices.
a

2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
39
Figure
2.7 The
partition
of the
2-sphere
(A)
into
an
open
2-cell
and a
vertex
violates
the
constraints
(2.2) and,
for
this
reason,
does
not
constitute
a
"cellular"
partition.
However,
such
a
partition
can be
modified
to
obtain
a
cellular
partition
(B)
honoring
the
constraints
(2.2).
•
P
n
(A)
is
defined
as the
family
of
subsets
of A
consisting
of all the
n-cells
contained
in
P(A):
Figure (2.13) gives
an
example
of
cellular partition
P(A)
of an 2
dimensional
object
A
embedded
in
1R
2
and its
associated
family
P%(A).
As
suggested
in
figures
(2.6)-A
and
(2.6)-C,
it
should
be
noted
that,
for a
given object
A
there
is,
in
general,
an
infinite
number
of
possible cellular
partitions
P(A).
Comments
1.
Any
partition
of a
manifold object
is not
necessarily
a
cellular
partition.
In
particular,
as
shown
in figure
(2.7)-A,
the
constraints (2.2)
may not
be
honored. However,
in
this case,
it is
always possible
to
modify
such
a
partition
to
obtain
a
cellular partition;
for
this
purpose,
as
shown
in
figure
(2.7)-B,
one
simply
has to
split
the
cells violating
the
constraints
(2.2).
2.
It
should
be
noted
that
P
n
(A)
is not a
partition
of A.
3.
The
constraints (2.2) were introduced
for the
sake
of
consistency with
the
constraint
(2.10),
which will
be
used
on
page
49 to
define
the
notion
of
CellView. Note
that
the
constraint
(2.10)
is in
turn
needed
to
define
the
notion
of
Vertex
View
adjacencies (see page 53).
4.
The
notion
of
"cellular partition"
as
defined
above
is
similar
to the
notion
of
regular
CW-Complex
6
introduced
by
Whitehead [231,
142].
6
Cellular
Whitehead
Complex.

40
CHAPTER
2.
CELLULAR PARTITIONS
Incidency
and
adjacency relationships
Two
cells
Ci
and
C%
belonging
to a
cellular partition
P(A)
are
said
to be
"incident"
if
they "touch" each other
in the
following
sense:
Two
cells
Ci
and
GI
belonging
to a
cellular partition
P(A]
are
said
to be
"ad-
jacent"
if
they
are
incident
and if, in
addition, they have
the
same topological
dimension:
Comment
It
should
be
noted
that,
for any
given cellular partition
P(A),
incidency
and
adjacency
of
cells describe
in
fact
the
same topological information:
• If all the
adjacency relationships between
the
cells
of
P(A)
are
known,
then
all the
incidency relationships
can be
retrieved:
• If all the
incidency relationships between
the
cells
of
P(A)
are
known,
then
all the
adjacency relationships
can be
retrieved:
Notion
of
n-simplex
Let
C be an
n-cell
of a
cellular partition
P(A).
By
definition,
we say
that
C
is
an
n-simplex (relatively
to
P(A))
if the
number
of
vertices
of C
contained
in
Po(A)
is
equal
to
(n
+ 1).
For
example,
in the
JR
space:
a
0-simplex
is a
"vertex,"
a
1-simplex
is an
"edge,"
a
2-simplex
is a
"triangle,"
and
a
3-simplex
is a
"tetrahedron."
2.3.3
Transforming
a
non-manifold
into
a
manifold
For
simplicity's sake,
in
this book, cellular partitions
are
only
denned
for
manifold
objects.
In
practice
it
should
be
noted, however,
that
this
is not
really
a
restriction;
let us
assume
that
P*(A*)
is a
partition
of a
non-manifold
object
A*
honoring
the
constraints (2.2)
and
such
that
In
this case,
as
suggested
in figure
(2.8),
we can
proceed
as
follows:
a
a

2.3.
CELLULAR
PARTITION
OF AN
N-MANIFOLD
OBJECT
41
Figure
2.8
Transforming
a
partition
P*(A*)
of
a
non-manifold object
A*
into
a
cellular
partition
P(A]
of
a
2-manifold
object
A
containing
A*.
The
virtual
cells
corresponding
to
{P(A)
—
P*(A*)}
are
represented
as
light grey areas, dashed lines,
and
a
white circle.
1.
Find
the
maximum dimension
n of the
cells
of
P*(A*).
2.
Choose
an (n +
l)-manifold object
A
containing
A*:
3.
Choose
a
cellular partition
P(A)
of A
containing
all the
cells
of the
cellular
partition
P*(A*):
The
elements
of
(P(A)
—
P*(A*))
may
always
be
considered
as
"virtual
cells,"
if
required,
as
suggested
in figure
(2.8).
It
should
be
observed,
however,
that
such
a
transformation
is
possible
only
o
if,
for any x
£A*,
the
local
topological
dimension
d(x)
honors
the
following
condition:
For
example,
such
a
transformation
is
possible
in the two
following
cases
frequently
encountered
in
subsurface
modeling:
• A*
consists
of the
(non-manifold)
set of
curves corresponding
to the
limits
of
the
geological facies
in a
cross section (see
figures
(2.2),
and
(2.17))
or a
geological map.
In
both cases,
the
curves
are
assumed
to lie on a
simply
connected surface
A
that
is
split into
parts
(2D
regions)
by
cells
of
A*.
• A*
consists
of the
(non-manifold)
set of
surfaces corresponding
to the
inter-
faces
between geological layers (see
figure
(2.1)).
These surfaces correspond
to
horizons
and
faults
and are
assumed
to lie
inside
a
simply connected volume
A
that
is
split into
parts
(3D
regions)
by
cells
of
A*.
It is
important
to
note
that
the
procedure
presented
above
for
transforming
a
non-manifold
object
into
a
manifold
object
is not
unique.
For
example,
in
[183],
Rossignac
and
Cardoz
propose
another
technique
based
on a
replication
of
some
cells
of the
non-manifold
object.

42
CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.9
Removing
the
light-grey
triangles
(A)
generates
a
non-manifold
topology
at the
location
corresponding
to the
black
vertex
(B).
However,
the new
non-manifold
object
so
obtained
can be
transformed
into
a
manifold
by
splitting
this
vertex
into twin
colocated
vertices
according
to
strategies
(C) or
(D).
A
practical
difficulty
As
shown above,
a
non-manifold object
can be
transformed into
a
manifold
object. Unfortunately,
the
reverse
is
also true:
it is
possible
that
a
manifold
object
becomes non-manifold
after
applying
a
topological operator whose pri-
mary purpose
was not to
make
this
object non-manifold.
For
example,
let
us
consider
the
triangulated surface shown
in figure
(2.9)-A.
Let us
assume
that
the two
triangles represented
in
light grey
are
removed:
as a
side
effect,
this removal
of
triangles generates,
at the
location corresponding
to the
black
vertex,
one of the
non-manifold situations referred
to in the top
part
of figure
(2.4).
However,
in
this case,
if the
vertex corresponding
to the
non-manifold
situation
is
split into twin
colocated
vertices, then this non-manifold situa-
tion
can be
avoided
by
applying
one of the two
following
strategies:
•
either,
as
shown
in figure
(2.9)-C,
we
assume
that
the two
triangles
holding
these
twin
vertices
are not
connected,
• or, as
shown
in figure
(2.9)-D,
we
transform
the two
triangles
into
two
rectan-
gles
sharing
a
common
degenerated
edge
corresponding
to
these
twin
vertices.
The
second strategy
is
similar
to the one
proposed
by
Rossignac
and
Cardoz
[183]
to
transform
a
non-manifold object into
a
manifold.
2.3.4
Abstract topological representations
This section shows
how any
cellular partition
of a
manifold object
can be
associated
in a
one-to-one
way to an
abstract
representation playing
the
role
of
"map"
of
this
partition. Such
a
representation
is at the
origin
of the
GMap
topological model, which will
be
presented
in
section
(2.4).

2.3. CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
43
Figure
2.10
Examples
of
isomorphic
cellular
partitions
P(A)
andP(B):
cells
of
these
two
isomorphic
partitions
are
associated
pairwise
by an
embedding
<j>
pre-
serving
the
incidency
relationships.
Isomorphisms
can
also
be
denned
from
P(A)
to
P(C)
and
from
P(B)
to
P(C}.
Isomorphic
cellular
partitions
As
shown
in
figure
(2.10),
let A and B be two
n-manifold
objects with cellular
partitions
P(A)
and
P(B],
respectively.
By
definition,
P(A]
and
P(B]
are
said
to be
0-isomorphic
or,
more simply, isomorphic
if
7
and if, in
addition, there
is a
series
of (n + 1)
mappings
(j>
=
{0o,
• •
-,
</>n}
honoring
the two
following
conditions
for any i £
{0,1,...,
n}:
1.
4>i
is a
bijection
between
Pi(A)
and
Pi(B}
associating each
^-cell
a G
Pi(A)
with
one
single
i-cell
b G
Pi(B],
and
conversely:
In
this
case:
• the set of
mappings
4>
is
called
an
isomorphism
between
P(A)
and
P(B),
and
7
Recall
that,
according
to the
definition
on
page
38,
'Pi(A)
represents
the set of all the
z-cells
in the
cellular
partition
P(A)
while
|"Pi(A)|
represents
the
number
of
elements
of
Pi(A}.
2.
If i > 0,
then,
for any
i-cell
a 6
Pi(A)
and any of its
incident
(i —
l)-cells
a'
G
Pi-i(A),
the
bijections
(pi
and
</>i_i
preserve
the
incidency
relationships:

44
CHAPTER
2.
CELLULAR PARTITIONS
an
i-cell
a
e
"Pi(A)
is
said
to be
isomorphic
8
to an
i-cell
b E
'Pi(B)
if
there
is a
mapping
0j
E
</>
such
that
6
=
</>i(a),
and
conversely.
For
example, with reference
to figure
(2.6):
the
cellular
partitions
P(A)
and
P(B)
are
isomorphic,
the
cellular
partitions
P(C}
and
P(D]
are
isomorphic,
and
the
cellular partitions
P(A)
and
P(C)
can not be
isomorphic because they
do not
have
the
same
number
of
cells.
It
should
be
noted
that
two
homeomorphic objects
A and B can be
associated
with
non-isomorphic cellular
partitions
as is the
case
for the
objects
in
figures
(2.6)-A
and
(2.6)-C.
Embeddings
Let
P(A)
be a
cellular partition
^-isomorphic
to a
cellular partition
P(B)
:
where
B is
assumed
to be a
subset
of E =
M
m
.
By
definition:
E is
called
an
embedding
space
of
P(A)
through
</>,
<p
is
called
an
embedding
of
P(A)
in the
embedding
space
E,
and
the
image
b =
(j>i(a)
of any
i-cell
a E Pi (A) is
called
an
embedding
of a in the
embedding
space
E.
As
shown
in figure
(2.10),
a
single cellular partition
P(A]
can
have multiple
embeddings.
Abstract
topological
representation
of a
cellular
partition
Note
that
an
isomorphism between
two
cellular partitions
is
given
if:
1.
there
is the
same
number
of
i-cells
in
both partitions
for
alH
>
0, and
2.
the
cells
can be
arranged
in
such
a way
that they
fulfill
the
conditions
(2.4),
and
(2.5).
The
above conditions
(1) and (2) are
purely combinatorial. They
do not
depend
on
"geometric properties" such
as the
exact shape
of the
cells
or the
dimension
of the
embedding
space.
Thus,
the
notion
of
isomorphism introduced above suggests
the
following
concept
for the
topological modeling
of any
manifold
object
A
associated
with
a
given cellular partition
P(A}:
To
each
i-cell
a E
Pi(A),
associate
an
arbitrary
and
distinct
element
a*
called
"abstract
i-cell"
and
define
the set
Qi(A)
as the
union
of all
these abstract
i-cells.
Define
the set
Q(A)
as the
union
of all the
sets
Qi(A):
Define
a
family
of
rules
"Incidencies"
on
Q(A)
reflecting
the
incidency
condi-
tions
(2.5) related
to
P(A).
8
Note
that,
in
this
case,
'P(A)
may be
identical
to
T'(B}
while
a is
different from
b.

2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
45
Figure
2.11
Depending
on the
dimension
of
the
embedding
space,
a
topological
object
may or may not
"geometrically"
self-intersect.
However,
from
the
topological
point
of
view,
such
a
geometrical
intersection
is not to be
considered
as
such.
Whatever model
(Q(A),
Incidencies)
is
chosen,
it
will
preserve
the
informa-
tion
related
to the
cellular partition
P(A).
Accordingly,
the
name
"abstract
topological representation"
ofP(A)
is
proposed
for
(Q(A),
Incidencies).
Conversely,
if A is an
n-dimensional
object belonging
to an
embedding
space
E =
M
m
,
then
P(A)
can be
thought
of as a
"geometric realization"
also called
an
"embedding"
of
(Q(A),
Incidencies) through
a
series
of (n + 1)
mappings
</>
=
{<^o,
• • •,
4>n}
honoring
the
following
conditions
that
mirror
the
constraints
(2.4),
and
(2.5):
1.
(j>i
is a
bijection
between
Qi(A)
and
Pi(A)
associating
each
abstract
i-cell
a*
€
Qi(A)
with
one
single
real
i-cell
a 6
Pi(A),
and
conversely:
2.
If i > 0,
then,
for any a*
e
Qi(A)
and any
a*'
e
Qi-i(A),
the
bijections
fa
and
fa-\
preserve
the
incidency
relationships:
Cornment
1:
Maps
and
Generalized
Maps
The
above concept
of
abstract
topological representation
of a
cellular
partition
is
at the
origin
of the
notions
of
"Maps"
and
"Generalized Maps" (GMaps)
presented
in
section
(2.4).
The
notion
of
Generalized
Map was
introduced
in
the
geometric modeling
field by
Lienhardt
in the
early 1990s [134, 135,
137, 138]
to
provide
a
rigorous algebraic
framework
for the
description
of the
topology
of a
cellular partition,
and it can
also
be
used
as the
backbone
of
software
implementation.

46
CHAPTER
2.
CELLULAR PARTITIONS
Comment
2:
Self-inter
sect
ions
of
embeddings
As
mentioned above,
an
abstract topological representation
of a
cellular par-
tition
P(A]
contains
all the
topological information concerning
the
neighbor-
hood
properties
9
of the
associated object
A.
Furthermore, such representation
allows
for
more
flexibility in
visualizing geometric objects,
and one can
"draw"
geometric intersections
that
"do not
count."
For
example,
figure
(2.11) shows
a
cellular partition
P(A)
of an
object
A and its
associated
abstract
represen-
tation
P*(A).
The 3D
object
A
does
not
self-intersect, while
its 2D
image
A'
does
and
appears
as a
non-manifold object. However,
carefully
interpreted
as
a
non-manifold object,
A'
represents
the
same topological properties
as the
manifold
object
A.
The
same trick
is
used
for a
representation
of the
Klein bottle represented
in
figure
(5.8).
The
Klein bottle
is
defined
as a
manifold object
in
JR
4
,
thus
it is
free
of
self-intersections.
The
self-intersection
of its
representation
in
7R
can be
neglected
if we
interpret
figure
(5.8)
as a
"projection"
of an
abstract
topological representation
of a
cellular partition
as we did
with
the
object
A'
above. Such representation
are
also called "immersions."
2.3.5
Euler-Poincare
theorem
Consider
a
cellular partition
P(A)
of a
manifold curve
A
into
a
series
of
adjacent curvilinear segments (edges) joining
a finite set of
points (vertices)
of
the
curve. Whatever
the
number
of
vertices
and
edges,
it is
obvious
that
•
if
the
curve
is
open,
then
the
number
of
vertices
(0-cells)
is
equal
to the
number
of
edges
(1-cells)
plus
one,
and
• if the
curve
is
closed,
then
the
number
of
vertices
(0-cells)
is
equal
to the
number
of
edges
(1-cells).
One
can
wonder whether similar relations exist
for
cells
of
surfaces and, more
generally,
for
cells corresponding
to a
cellular partition
of any
manifold object.
The
Euler-Poincare theorem gives
an
elegant answer
to
this
question:
Theorem
Let
A be a
manifold object.
For any
cellular partition
P(A)
of
.A,
the
Euler-
Poincare characteristic
%(A),
defined
by
is
independent
ofP(A).
If
A is an
n-manifold
object, then
it is
easy
to
check
that
x(A)
can
also
be
9
It
should
be
noted,
however,
that advanced topological concepts
like
"knots"
are not
taken
into account
by
such
a
representation (see
[8]).
For
example,
the
topological model
presented
in
this book makes
no
distinction between
a
simple torus
and a
torus with
one
or
several knots.

2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
47
Figure
2.12
Examples
of
cellular
partitions
of
open
surfaces:
the
Euler-Poincare
characteristic
x
=
V
—
E + F is
equal
to 2
minus
the
number
of
boundaries
whatever
the
cellular
partition.
written
as
follows
where
7^(^4)1
represents
the
number
of
i-cells
in
P(A).
Examples
The
formal proof
of
this general
form
of the
Euler-Poincare theorem
is
based
on the
theory
of
homology,
which
is far
outside
the
scope
of
this book
[105].
However,
we can
easily
verify
the
correctness
of
this theorem using examples
such
as, for
example, those presented
in figures
(2.6),
and
(2.12).
The
case
of
2-manifolds
As
suggested
in figures
(2.6),
and
(2.12),
in the
special case
of a
2-manifold
surface
A,
the
Euler-Poincare characteristic
can be
written:
It is
also possible
to
show
that
x(A)
can be
decomposed into
an
alternate
sum
of
three numbers
{xi(A)
: i =
0,1,
2}
called
"Betti
numbers"
[105]:
