Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


48
CHAPTER
2.
CELLULAR PARTITIONS
More
generally, Betti numbers
are
denned
for any
n-manifold object
A as
the
ranks
of the
homology group
of A and
were proved
to be
invariant
by
Poincare [176,
229].
These Betti numbers were used
by
Poincare
to
prove
the
formula
(2.8) extending
to any
n-manifold object
the
formula (2.9) previously
discovered
by
Descartes
and
Euler.
Another
famous topological invariant
of a
2-manifold
surface
A is its
"genus"
g(A)
denned
as the
largest number
of
non-intersecting, simple closed
curves
that
can be
drawn
on A
without dividing
it
into
two
parts.
It can
be
noted
that
g(A)
also represents
the
number
of
"handles"
of A:
cutting
a
handle does
not
divide
A
into
two
parts
and
simply generates
2
holes.
For
any
closed connected
orientable
10
surface
A of
genus
g(A),
it can be
shown
that
the
Betti numbers
are
This explain
why the
closed surfaces without handles represented
in
figure
(2.6)
have
an
Euler-Poincare characteristic
x(A]
equal
to 2.
If
AI
and
A
2
are two
manifold surfaces, then
it can be
shown
[2]
that
the
Betti numbers characterize homeomorphisms between
AI
and
A?
in the
following
sense:
Historical
note
In the
case where
A is
a.
closed surface
homeomorphic
to a
2-sphere, formula
(2.9)
reduces
to the
famous Euler
formula:
This remarkable result, which
is the
earliest discovery
in
topology,
is due to
Descartes
who
established
it in
1639
but the
formula bears
the
name
of
Euler
who
rediscovered
it and
published
a
proof
in
1751.
Application
to
geomodeling
From
a
practical point
of
view,
in a
modeling system,
the
Euler-Poincare
formula
(2.8)
can be
used
to
control
the
consistency
of
operators transforming
a
cellular partition
P(A)
of a
manifold
object
A
into
a
cellular partition
P(A'}
of
another manifold object
A'.
For
example,
if an
operator
T
adds
a
vertex
V to a
cellular partition
of
a
manifold
surface
A,
then, according
to
(2.9),
the
cellular partition
of the
resulting surface
A'
=
T(A\V) must preserve
the
relationship
x(A)
=
x(A')-
This implies
that
the
operator
T can be
implemented,
for
example, according
to one of the
following
procedures:
•
Create
one new
triangular
face
incident
to an
edge
on the
boundary
of A
with
two
new
edges
and one new
vertex
V.
•
Split
(kill)
one
edge
and
replace
it by two new
edges
with
a
common
new
vertex
V.
10
For
a
definition
of the
notion
of
orientability,
see
pages
68 and
218.

2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
49
•
Split
(kill)
a
face
with
n
vertices
and
replace
it by n new
triangular
facets
with
n new
edges
and one new
common
vertex
V.
Such
operators preserving
the
Euler-Poincare
characteristic
are
referred
to as
"Euler
operators"
in the
literature
[152].
2.3.6
Notion
of
CellView
As
shown
in
figure
(2.13),
consider
a
cellular partition
of a
manifold object
A
consisting
of two
adjacent polygonal facets
F\
and
F%
that
share
a
common
edge
E,
and let
V\
and
Vz
be the two
vertices corresponding
to the end
points
(boundary)
of
E:
• The
common
edge
E can be
viewed
either
as an
element
of the
boundary
of
jFi
or as an
element
of the
boundary
of
F^;
these
two
different views
of the
same
object
can be
coded
as
follows:
•
Each
common
vertex
Vi (i G
{1,2})
can be
viewed
either
as an
element
of the
boundary
of the
boundary
E of
F\
or, as an
element
of the
boundary
of the
boundary
E of
F%
as
follows:
This
recursive concept
of a
"cell viewed
from
another cell," also referred
to as
"Cell-Tuple-Structure"
in the
literature,
was
introduced
by
Brisson [35,
36, 37]
as a key
element
to
describe cellular partitions. This section
is a
general
presentation
of
this important concept.
Definitions
Let
P(A)
be a
given cellular partition
of an
n-manifold
object
A and let v be
a
nonempty list
of
cells
of
P(A):
By
definition,
v is
called
a
"CellView"
of
CQ
from
C
n
or,
more simply,
a
CellView,
if the two
following
conditions
11
are
honored:
Moreover,
the
cell corresponding
to the
head
of
v is
referred
to as
view
edC
ell
(v):
Depending
on the
dimension
of
viewedCell(v),
one can say
that
11
Note
that
these conditions
are
consistent with constraints
(2.2).
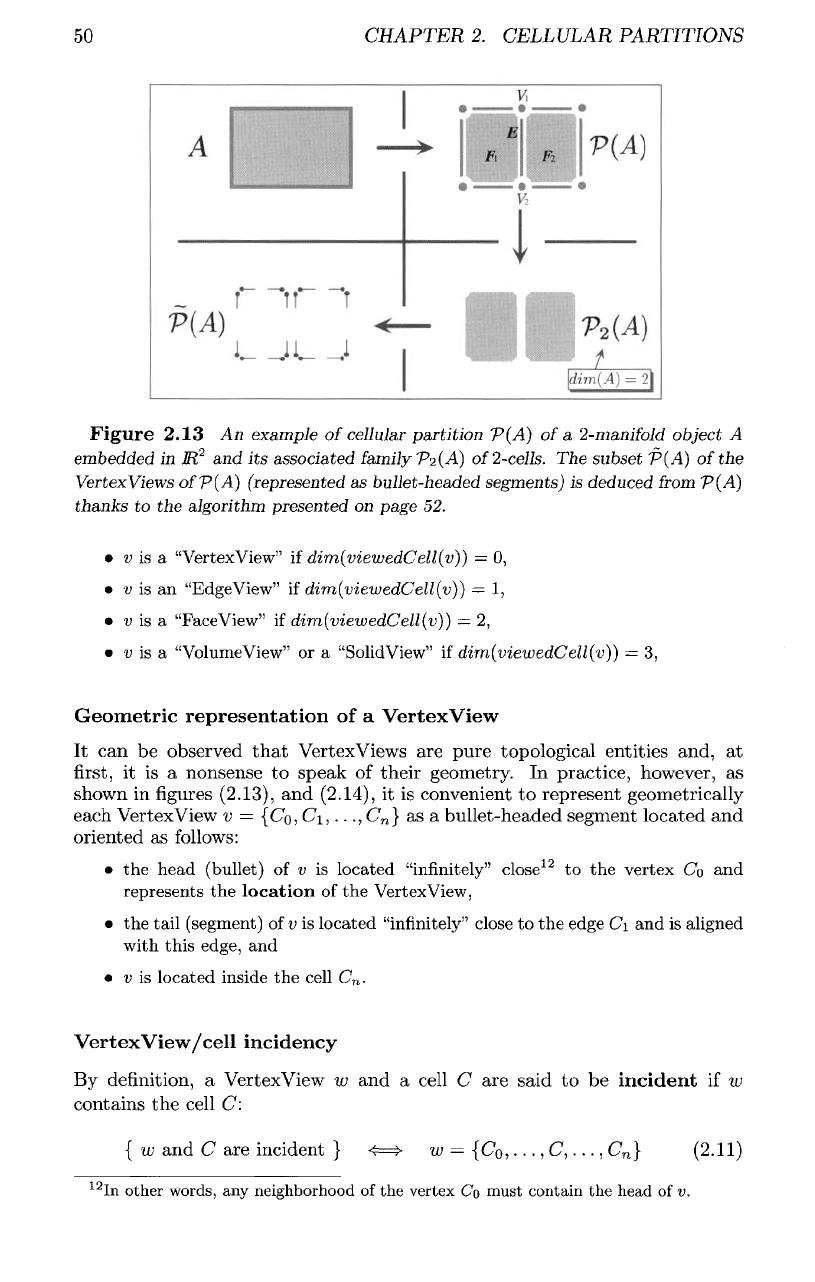
50
CHAPTER
2.
CELLULAR
PARTITIONS
Figure
2.13
An
example
of
cellular
partition
P(A)
of
a
2-manifold
object
A
embedded
in
JR
2
and its
associated family
P-z(A)
ofl-cells.
The
subset
P(A)
of
the
Vertex
Views
ofP(A)
(represented
as
bullet-headed segments)
is
deduced from
P(A)
thanks
to the
algorithm presented
on
page
52.
• v is a
"VertexView"
if
dim(viewedCell(v))
= 0,
• v is an
"EdgeView"
if
dim(viewedCell(v))
= 1,
• v is a
"FaceView"
if
dim(viewedCell(v))
= 2,
• v is a
"VolumeView"
or a
"SolidView"
if
dim(viewedCell(v))
= 3,
Geometric
representation
of a
VertexView
It can be
observed
that
VertexViews
are
pure
topological
entities
and,
at
first, it is a
nonsense
to
speak
of
their
geometry.
In
practice,
however,
as
shown
in figures
(2.13),
and
(2.14),
it is
convenient
to
represent
geometrically
each
VertexView
v =
(Co,
C*i,...,
C
n
}
as a
bullet-headed
segment
located
and
oriented
as
follows:
• the
head (bullet)
of v is
located "infinitely"
close
12
to the
vertex
Co and
represents
the
location
of the
VertexView,
• the
tail (segment)
of v is
located "infinitely" close
to the
edge
C\
and is
aligned
with
this edge,
and
• v is
located inside
the
cell
C
n
.
VertexView/cell
incidency
By
definition,
a
VertexView
w
and a
cell
C are
said
to be
incident
if
w
contains
the
cell
C:
12
In
other words,
any
neighborhood
of the
vertex
Co
must contain
the
head
of v.
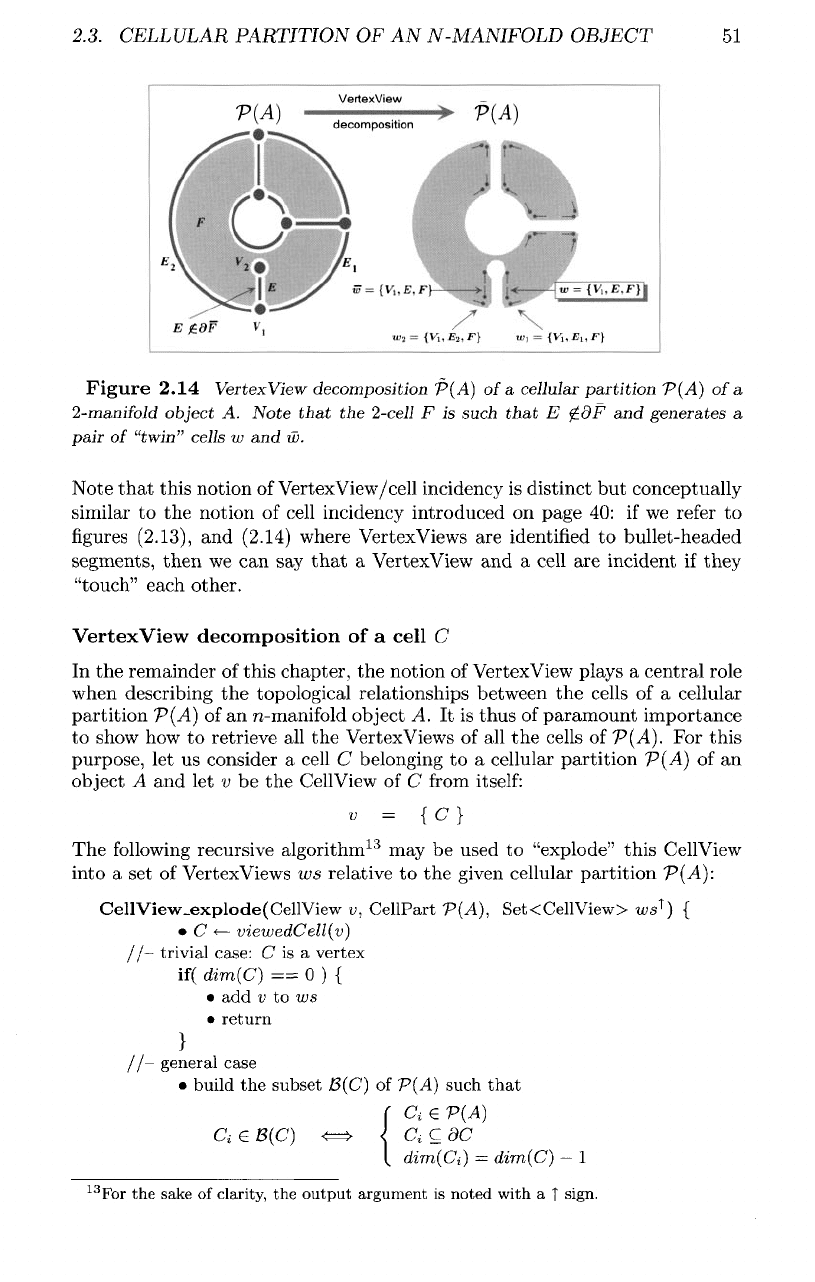
2.3. CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
51
Figure
2.14
Vertex
View
decomposition
P(A)
of
a
cellular
partition
P(A)
of
a
2-manifold
object
A.
Note
that
the
2-cell
F is
such
that
E
£dF
and
generates
a
pair
of
"twin"
cells
w
and
w.
Note
that
this notion
of
Vertex
View/cell incidency
is
distinct
but
conceptually
similar
to the
notion
of
cell incidency introduced
on
page
40: if we
refer
to
figures
(2.13),
and
(2.14)
where VertexViews
are
identified
to
bullet-headed
segments,
then
we can say
that
a
Vertex
View
and a
cell
are
incident
if
they
"touch" each other.
Vertex
View
decomposition
of a
cell
C
In the
remainder
of
this chapter,
the
notion
of
VertexView plays
a
central role
when
describing
the
topological relationships between
the
cells
of a
cellular
partition
P(A)
of an
n-manifold
object
A. It is
thus
of
paramount importance
to
show
how to
retrieve
all the
VertexViews
of all the
cells
of
P(A).
For
this
purpose,
let us
consider
a
cell
C
belonging
to a
cellular partition
P(A)
of an
object
A and let v be the
CellView
of C
from
itself:
The
following
recursive
algorithm
13
may be
used
to
"explode" this CellView
into
a set of
VertexViews
ws
relative
to the
given cellular partition
P(A}:
13
For
the
sake
of
clarity,
the
output argument
is
noted with
a
|
sign.

52
CHAPTER
2.
CELLULAR PARTITIONS
for_all(
Cell
d
e
B(C)
) {
if(
d
G
dC
)
niter
<-
1
else
niter
<-
2
for(
iter=l
;
iter<niter
;
iter++
) {
//<
inner
loop
•
build
new
CellView
Vi =
copy
of v
•
insert
d at
head
of
Vi\
Vi
<—
{Ci,
Vi}
•
CellView_explode(
Vi,P(A),ws
)
}
}
}
Notion
of
twin
Vertex
Views
In
the
above algorithm,
the
purpose
of the
inner loop controlled
by the
pred-
icate
(d G
dC}
is to
duplicate
the
CellView
v^
when
Ci is an
"internal" cell
of
A
that
is
used twice
by C as a
boundary. This allows cells such
as
those
corresponding
to the
internal
edge
14
E in the
left-hand side
of figure
(2.14)
to
be
"exploded"
in a
consistent way.
As a
result,
the
above algorithm generates
a
pair
of
"twin" VertexViews noted
w
and
w,
respectively,
and
consisting
of
copies
of
exactly
the
same list
of
cells:
As
shown
in figure
(2.14),
the
geometric representations
of
such twin Ver-
texViews
are
assumed
to be
located
in
C
n
in
such
a way
that
the
shortest
path
between them, within
C
n
,
crosses
C
n
-\.
Set
P(A)
of the
Vertex
View's
of a
cellular
partition
P(A)
Let
P(A)
be a
given cellular partition
of a
manifold object
A. By
definition,
the set of all the
VertexViews
of
P(A)
is
noted
as
P(A).
Figure (2.13) shows
an
example
of
such
a set
P(A)
in the
case
of an
object
A
embedded
in
JR
2
.
It is
always possible
to use the
following
algorithm
15
for
"exploding"
P(A)
into
a set
P(A)
of
elementary "bricks" corresponding
to
VertexViews:
CellPart_explode(CellPart
P(A),
Set<CellView>
P(A)
T
) {
•
P(A)
<—-
empty
set
• n
«—
dim(A)
for_all(
Cell
C
e
P
n
(A)
) {
•
build
new
CellView
v
•
initialize
v: v
<—
{ C }
•
CellView_explode(
v,P(A),P(A)
)
}
}
It
should
be
observed
that
this algorithm assumes
that
the
cellular partition
P(A)
of the
object
A to be
exploded already exists
and is
given. This means
that
14
See
also
the
"free
edge"
in figure
2.17.
15
For
the
sake
of
clarity
the
output argument
is
noted
with
a
|
sign.

With such
a
definition,
it can be
observed
that
twin
Vertex
Views
(w,w),
as
defined
on
page
52, are
z-adjacent
for any i.
Moreover, each twin
Vertex
View
w
(resp.
w)
may be
z-adjacent
with
a set of one or
several VertexViews
{w'i,
w'
2
,..
.}[i]
different
from
its
twin
w
(resp.
w). In
such
a
case,
to
keep
only
one
«-adjacency
per
twin
Vertex
View,
it is
proposed
to
proceed
as
follows:
1.
cancel
all the
i-adjacencies
of w
(resp.
tD);
2.
restore
the
i-adjacency
of w
(resp.
w)
with
the
"closest"
Vertex
View
w'j
taken
in the set
{u>i,u>2,
• •
-}[z]-
2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
53
•
this
algorithm
is a
descriptive
algorithm
showing
how to
deduce
the set
P(A)
of
VertexViews
from
a
given
cellular
partition
P(A)
of an
object
A, and
•
this
algorithm
cannot
be
used
to
construct
a
cellular
partition
P(A)
as-
sociated
with
a
given
object
A
from
scratch.
However,
from
a
theoretical point
of
view,
this algorithm
is
extremely
im-
portant because
it
shows
that
any
cellular partition
P(A)
can be
recursively
decomposed into
a set of
VertexViews whatever
the
object
A and the
dimen-
sion
of the
embedding space (see
figure
(2.13)).
In
other words, this algorithm
shows
that
the
topology
of any
cellular partition
of a
manifold object
can be
represented
by a set of
VertexViews plus adjacency relations
that
will
be
pre-
sented
in the
next section.
Prom
a
computer science point
of
view,
this opens
the
door
to a
unified
topological model where
the
topological database contains only
one
type
of
object
corresponding
to
VertexViews.
In
section
(2.4),
we
will present such
a
topological model based
on
this observation
and
composed
of:
• a
unique
elementary
data type
called
"Dart,"
consisting
of an
abstract
repre-
sentations
of
VertexViews,
and
• an
algebraic structure, called
"GMap,"
playing
the
role
of a
database
and
consisting
of a set of
Darts
plus
a set of
operators
that
allow
navigation
from
a
Dart
to its
neighboring
Darts.
2.3.7
VertexView adjacencies
This section shows
how
VertexViews
can be
used
to
describe adjacencies
be-
tween
the
cells
of a
cellular
partition
P(A)
of an
n-manifold
object
A:
Notion
of
i-adjacency
between
VertexViews
Let
us
consider
two
VertexViews
w and
w'
belonging
to
P(A):
By
definition,
we
will
say
that
w 6
P(A)
and
w'
6
P(A)
are
i-adjacent
if
they
share
the
same
n-cells
for any n
^
i. In
other words,
we
have:
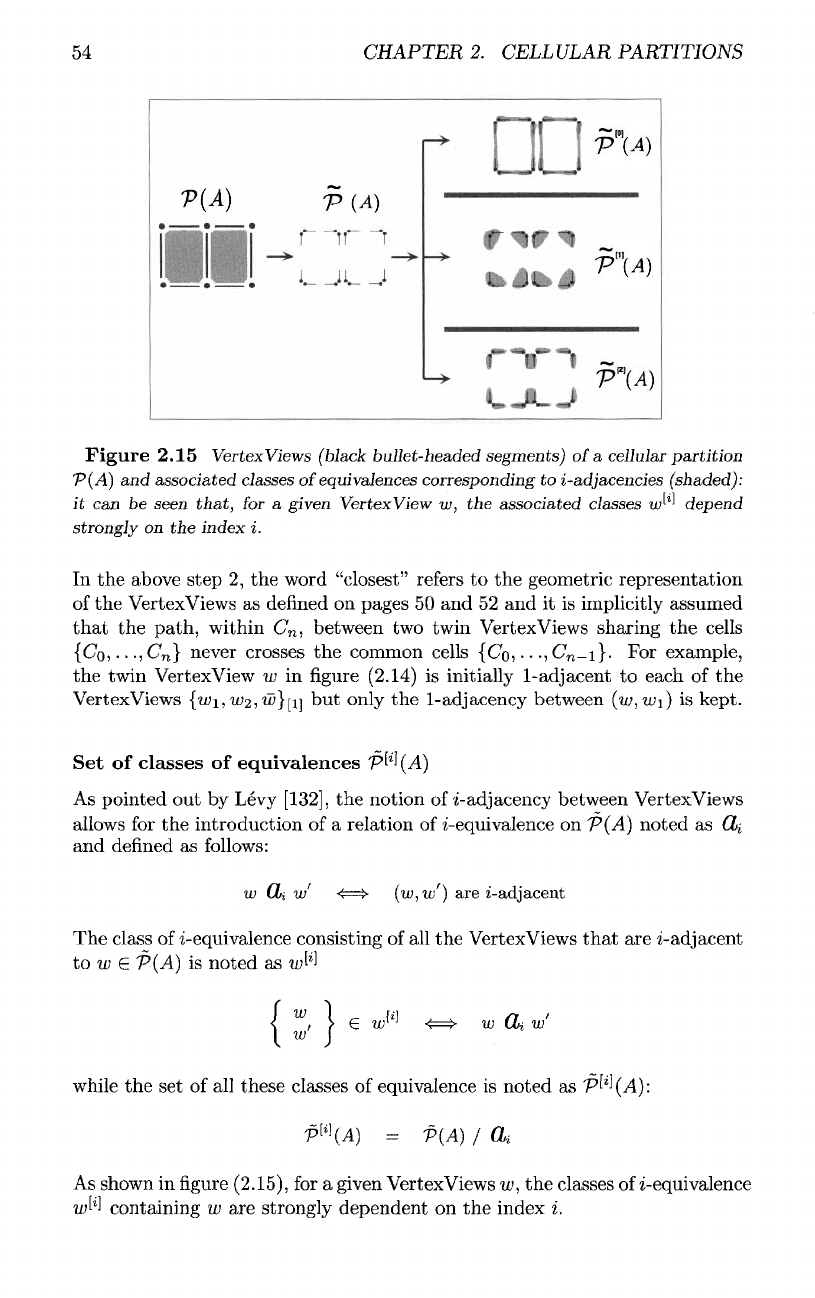
54
CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.15
Vertex
Views
(black
bullet-headed
segments)
of
a
cellular
partition
P(A)
and
associated
classes
of
equivalences
corresponding
to
i-adjacencies
(shaded):
it can be
seen
that,
for a
given
VertexView
w,
the
associated
classes
w*-
1
'
depend
strongly
on the
index
i.
In the
above step
2, the
word "closest"
refers
to the
geometric representation
of
the
Vertex
Views
as
defined
on
pages
50 and 52 and it is
implicitly assumed
that
the
path, within
C
n
,
between
two
twin VertexViews sharing
the
cells
(Co,...,
C
n
}
never crosses
the
common cells
{Co,
•
•.,
C
n
_i}.
For
example,
the
twin VertexView
w in figure
(2.14)
is
initially
1-adjacent
to
each
of the
VertexViews
{wi^w^^w}^
but
only
the
1-adjacency
between
(w,wi]
is
kept.
Set of
classes
of
equivalences
P^
(A)
As
pointed
out by
Levy
[132],
the
notion
of
i-adjacency
between VertexViews
allows
for the
introduction
of a
relation
of
i-equivalence
on
P(A)
noted
as
CLi
and
defined
as
follows:
while
the set of all
these classes
of
equivalence
is
noted
as
P^(A):
As
shown
in figure
(2.15),
for a
given VertexViews
w, the
classes
of
^-equivalence
iuM
containing
w are
strongly dependent
on the
index
i.
The
class
of
z-equivalence
consisting
of all the
VertexViews
that
are
i-adjacent
to w
G
P(A)
is
noted
as
iyW
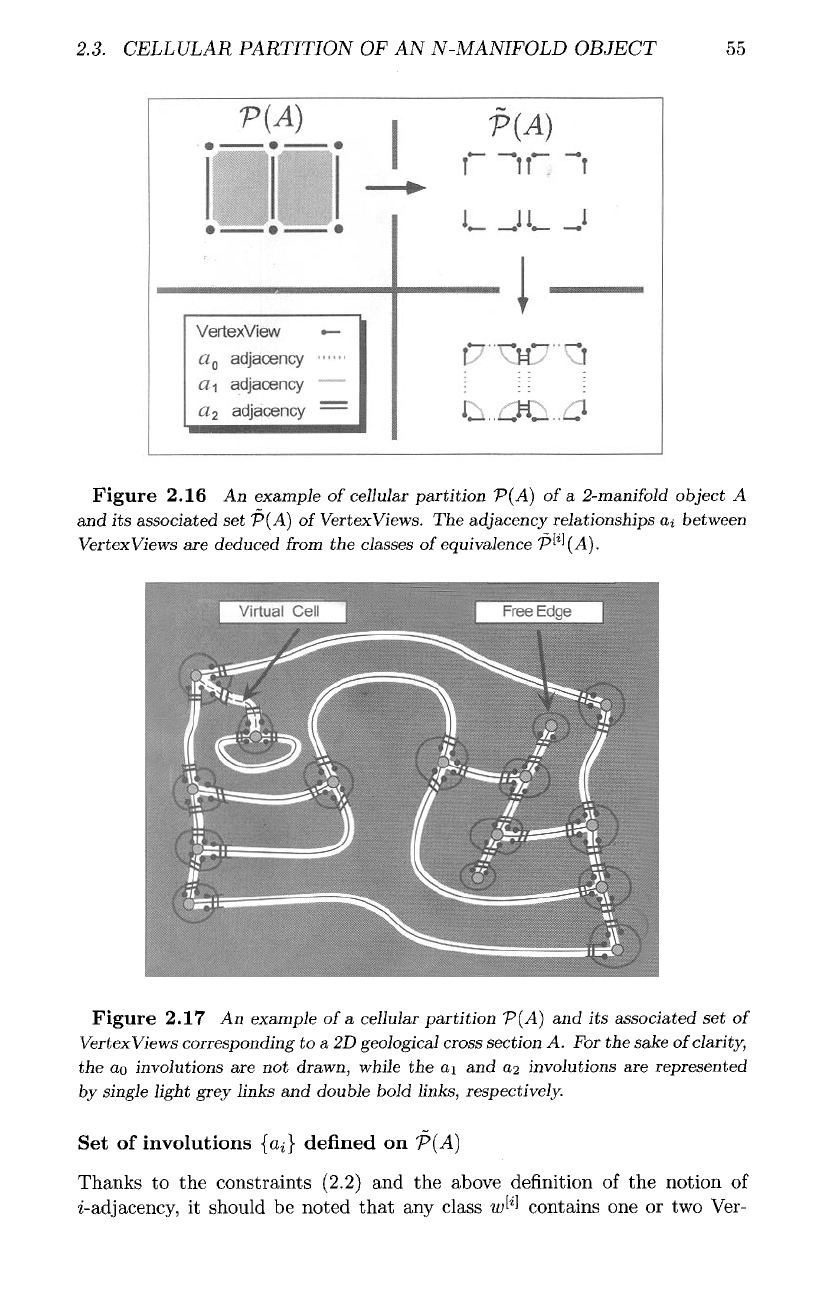
2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
55
Figure
2.16
An
example
of
cellular
partition
P(A)
of a
2-manifold
object
A
and
its
associated
set
P(A)
of
Vertex
Views.
The
adjacency relationships
at
between
Vertex
Views
are
deduced
from
the
classes
of
equivalence
P^'(A).
Figure
2.17
An
example
of
a
cellular
partition
P(A)
and its
associated
set of
Vertex
Views
corresponding
to a 2D
geological cross section
A. For the
sake
of
clarity,
the
ao
involutions
are not
drawn, while
the
ai
and
0,2
involutions
are
represented
by
single light grey links
and
double bold links, respectively.
Set of
involutions
{a^}
defined
on
P(A)
Thanks
to the
constraints (2.2)
and the
above
definition
of the
notion
of
z-adjacency,
it
should
be
noted that
any
class
w^
contains
one or two
Ver-

56
CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.18
The
upper
part
of (A)
shows
the
a\
and
0,2
involutions
associated
with
Vertex
Views corresponding
to a
pair
of
adjacent
tetrahedra.
The
lower
part
of
(A)
is an
exploded
view
of
these
two
tetrahedra showing
the
as
links;
the ao
links
are
not
represented, while
the
a»
links
are
represented
by i
parallel
segments
for
i > 0.
Part
(B)
shows
an
exploded
view
of a
solid consisting
of
polyhedral cells
where only
the
as
involutions
are
represented.
tex
Views:
As
shown
in
figure
(2.16),
this suggests introducing
a
transformation
a^
from
P(A)
to
itself
denned
as
follows:
For any
index
i
>
0, the
transformation
o,i
so
defined
is an
involution
16
called
i-adjacency
on
P(A):
From
a
graphical point
of
view,
as
shown
in figures
(2.14),(2.15),
(2.16),
(2.17),
and
(2.18),
the
following
notations
will
be
used:
• A
class
of
equivalence
w^
=
{w,w'}
or,
equivalently,
the
associated
involution
o^,
will
be
represented
by
a
dashed
segment
if i = 0,
one
solid
line
if i =
1,
two
solid lines
if i — 2, and
three
solid
lines
if i = 3.
• For
simplicity's sake,
in the
case where
w^
=
{w}
contains only
one
VertexView,
the
associated involution
will
not be
represented.
16
An
involution
is a
transformation
T
that
is
equal
to its own
inverse:
T
=
T
l
.

2.4.
2. 4
Generalized
Maps
As
previously mentioned page
45, in the
geometric modeling
field, the
notion
of
Generalized
Map
(GMap)
was
introduced
by
Lienhardt
17
in the
early 1990s
[134,
135, 137, 138]
to
provide
a
rigorous algebraic framework
for the
descrip-
tion
of the
topology
of a
cellular partition
P(A)
through
its set of
Vertex
Views
and its
associated
involutions
{«»}.
It
should
be
noted
that
the
notion
of
Generalized
Map is
similar
and
equivalent
to the
concept
of
"Cell-Tuple-Structure"
independently introduced
by
Brisson [35,
36,
37].
2.4.1
GMap associated with
a
cellular partition
P(A)
Definition
1
Let
n
>
0 be a
given integer
and let
G(D,
a
0
,0:1,...,
a
n
)
be a (n +
2)-tuple
such
that
By
definition,
in the
frame
of
this book,
we
will
say
that
G(D,
ao,
ai,...,
a
n
)
is
a
"Generalized Map"
of
dimension
n or,
more simply,
an
n-GMap
or a
GMap
if the
three
following
constraints
are
honored:
1.
The
involutions
{ao,
ai,...,
o-n-i}
do not
have
any fixed
point
on D:
2.
The
transformations
{oti
ooci+2+k}
are
involutions
for any i
>
0 and any
k>0:
3.
The
transformations
{«j
oa^
+2+
fc}
have
no fixed
point
for any i
>
0 and
any
k
>
0:
Figure (2.19) shows examples
of
0-GMap,
1-GMap,
and
2-GMap.
17
GMaps
are
derived
from
the
concept
of
"Combinatorial-Map"
introduced
by
Edmonds
[72]
and
used
for
modeling
subdivisions
of
surfaces
[112, 135,
221].
GENERALIZED MAPS
7
57
57
