Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

58
CHAPTER
2.
CELLULAR PARTITIONS
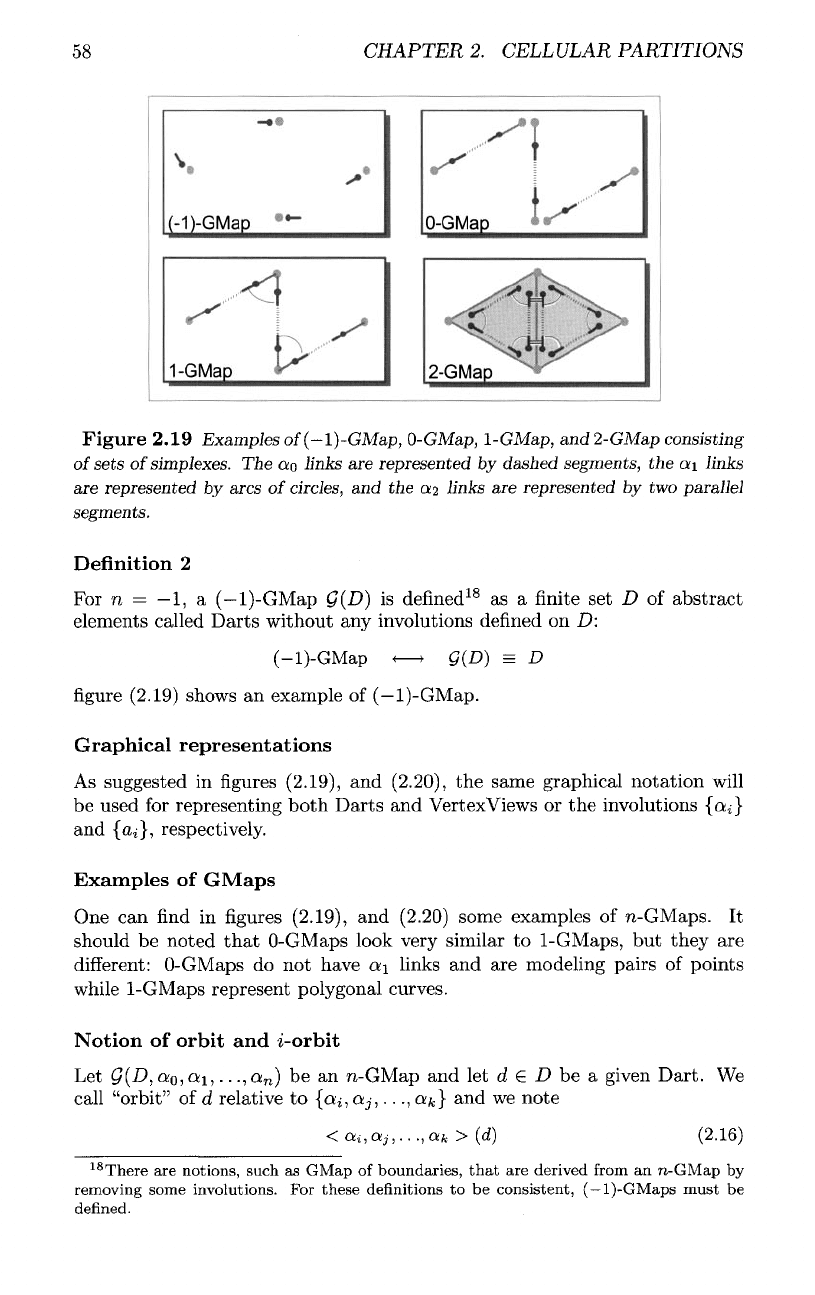
Figure
2.19
Examples
of
(-l)-GMap,
0-GMap,
1-GMap,
and
2-GMap
consisting
of
sets
of
simplexes.
The
ao
links
are
represented
by
dashed
segments,
the
a\
links
are
represented
by
arcs
of
circles,
and the
ct?
links
are
represented
by two
parallel
segments.
Definition
2
For n =
—
1, a (
—l)-GMap
Q(D]
is
defined
18
as a finite set D of
abstract
elements
called Darts without
any
involutions
defined
on D:
figure
(2.19)
shows
an
example
of
(—l)-GMap.
Graphical
representations
As
suggested
in figures
(2.19),
and
(2.20),
the
same
graphical
notation
will
be
used
for
representing
both
Darts
and
Vertex
Views
or the
involutions
{on}
and
{fli},
respectively.
Examples
of
GMaps
One can find in figures
(2.19),
and
(2.20)
some examples
of
n-GMaps.
It
should
be
noted
that
0-GMaps look very similar
to
1-GMaps,
but
they
are
different:
0-GMaps
do not
have
0,1
links
and are
modeling pairs
of
points
while
1-GMaps represent polygonal curves.
Notion
of
orbit
and
i-orbit
Let
C?(£>,0!o,ai,
• •
-,<^n)
be an
n-GMap
and let d
e
D be a
given Dart.
We
call
"orbit"
of d
relative
to
{a^,
a-/,...,
a/t}
and we
note
18
There
are
notions, such
as
GMap
of
boundaries, that
are
derived
from
an
n-GMap
by
removing
some involutions.
For
these
definitions
to be
consistent,
(—l)-GMaps
must
be
denned.
2.4.
GENERALIZED MAPS
59
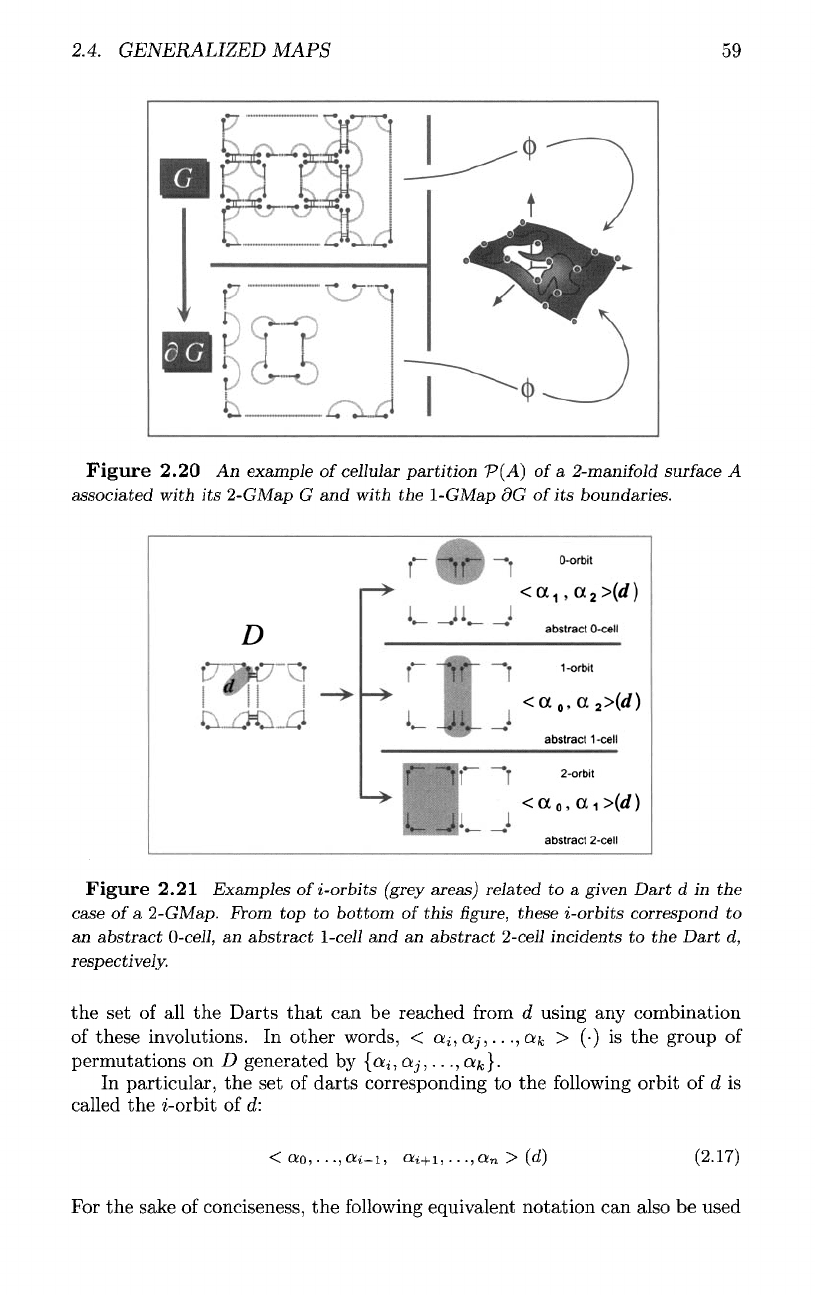
Figure
2.20
An
example
of
cellular partition
P(A)
of
a
2-manifold
surface
A
associated
with
its
2-GMap
G and
with
the
1-GMap
dG
of
its
boundaries.
Figure
2.21 Examples
ofi-orbits
(grey
areas)
related
to a
given Dart
d in the
case
of a
2-GMap. From
top to
bottom
of
this
figure,
these i-orbits correspond
to
an
abstract
0-cell,
an
abstract
1-cell
and an
abstract
2-cell
incidents
to the
Dart
d,
respectively.
the set of all the
Darts
that
can be
reached
from
d
using
any
combination
of
these
involutions.
In
other
words,
<
Oj,
CKJ,...,
&k
> (•) is the
group
of
permutations
on D
generated
by
{0:$,
QJ,
...,
o^}.
In
particular,
the set of
darts
corresponding
to the
following
orbit
of d is
called
the
i-orbit
of d:
For the
sake
of
conciseness,
the
following
equivalent
notation
can
also
be
used

60
CHAPTER
2.
CELLULAR PARTITIONS
to
characterize
the
i-orbit
of
d:
Figure
(2.21)
shows some examples
of
«-orbits.
GMap
of the
boundaries
Let
G =
Q(D,aQ,ai,..
.,a
n
)
be a
given
n-GMap
(see
figures
(2.20),
and
(2.22)).
By
definition,
the (n -
l)-GMap
is
called "GMap
of the
boundaries"
of G if
D'
and the
{o^j's
are
such
that
• for any
Dart
d G
D',
the
involution
o4-i
is
such
that
Dual
of a
GMap
By
definition,
the
dual
of an
n-GMap
G(D,
QJQ,
ai,...,
a
n
]
is
also
an
n-GMap
G(D*,
O!Q,
a
i>
• •
•>
a
n)
suc
h
that
Open
and
closed GMap
Sewn
and
free
Darts
Let
Q(D,ao,ai,..
.,cc
n
)
be an
n-GMap
and let d € D be a
given Dart;
by
definition:
2.4.2
Cellular
synthesis
The
entire section
(2.3)
was
dedicated
to the
decomposition
of a
manifold
object
into cells whose adjacencies where represented
by a set of
Vertex
Views
and
involutions.
In
this
section
we
present
the
opposite point
of
view which
consists
in
rebuilding
a
cellular partition
P(A)
from
an
abstract representation
consisting
of a
GMap.

2.4.
GENERALIZED
MAPS
61
Figure
2.22 Decomposition
of
a
solid
into polyhedric cells
(A)
represented
by
a
GMap
and its
associated boundary
(B)
also represented
by a
GMap.
Notion
of
"abstract"
i-cell
Comparing
figures
(2.15),
and
(2.21)
allows
a
strong
analogy
between
an i-
orbit
in a
GMap
and a
i-cell
in a
cellular
partition
to be
pointed
out.
This
suggests
introducing
the
notion
of
"abstract"
i-cell
as
follows:
By
definition,
in a
GMap
G
=
Q(D,
ao,
cui,...,
a
n
),
any
i-orbit
of a
Dart
d
G
D
is
called
an
"abstract"
i-cell
of G
incident
to
d:
Brisson-Lienhardt
theorem
As
suggested
in
figure (2.20),
any
n-GMap
G =
Q(D^o.Q
1
a\^..
.,a
n
)
can be
associated
with
a
cellular
partition
P(A)
of an
n-manifold
object
A in
such
a
way
that
•
There
is a
one-toone
mapping
0
from
D to the set of
Vertex
Views
P(A):
• If
{ao,...,
a
n
}
are the
involutions corresponding
to the
adjacencies
defined
on
P(A),
then,
for any
integer
i € [0,
n],
the
above one-to-one mapping
0 is
such
that
• The
above
one-to-one
mapping
0 has (n + 1)
components
{</>o,...,
</>
n
}
such
that
<pi(d]
is the
z-cell
contained
in the
Vertex
View
w =
4>(d}\
• The
ith
component
<f>i
of the
above one-to-one mapping
</>
establishes
a
one-to-
one
correspondence between
the
"abstract"
i-cells
of G and the
"real"
z-cells
ofP(A):

62
CHAPTER
2.
CELLULAR
PARTITIONS
• The
above
one-to-one
mappings
(0o,
• •
•,
</>n-i}
establish
a
one-to-one
cor-
respondence
between
the
"abstract"
?-cells
of dG and the
"real"
z-cells
of
(P(A)
n
dA).
(see
examples
in figures
(2.20),
and
(2.22)).
This
fundamental theorem
is a
direct consequence
of the
concept
of
abstract
topological
representation
of a
cellular partition introduced
on
page
44 and is,
in
fact,
a
compilation
of
several theorems
due to
Brisson
and
Lienhardt (see
[35,
37,
138]).
Interpretation
of
Brisson-Lienhardt
theorem
If
we
refer
to the
definition
of
isomorphism presented
on
page
43, one can
observe
that
the
above Brisson-Lienhardt theorem
can be
seen
as
introducing
an
isomorphism
0
from
an
"abstract"
GMap
<?(!),
ao,ai,..
.,a
n
)
to a
"real"
GMap
£(P(A),a
0
,ai,...,a
n
):
This suggests considering
the
valuated graph
G =
(?(£),
a
0
,ai,..
.,a
n
]
as a
representation,
in an
abstract
space,
of the
topology
of a
cellular
partition
P(A)
of a
real
manifold
object
A
belonging
to the
embedding space
IR
m
.
In
such
a
representation:
• The
VertexViews
associated
with
P(A)
are the
images
of the
Darts
of
D:
• The
"real"
i-cells
of
'P(A)
are the
images
of
"abstract"
^-cells
of G by the
component
^
of 0 =
{(/>o,...,
0
n
}:
According
to
Brisson-Lienhardt theorem, each
"abstract"
i-cell
consists
in the
set of
Darts whose images
are the
VertexViews incident
to its
associated real
•i-cell
in the
embedding space
M
m
.
Conversely,
the
definition
of a
"real"
i-cell
as
the
image
by fa of an
"abstract"
i-cell
can be
considered
as a
"cellular
synthesis."
It
should
be
noted, however,
that
a
representation
of an
entity
is not the
entity
itself.
In
particular,
a
Dart
is an
abstract entity
that
is
different
from
a
Vertex
View,
and,
from
a
practical
point
of
view,
this
means
that
A
Dart represents
a
sorted list
of
cells
but, contrary
to a
Ver-
tex
View,
a
Dart
does
not
consist
of
a
sorted list
of
cells.

2.4.
GENERALIZED MAPS
63
Figure
2.23
An
example
of
a
pair
of
adjacent
2-cells
whose
i-embeddings
are
consistent
for i = 0 and
inconsistent
for i = 1.
Implementing
0
=
{</>o,...,
</>
n
}
as a
list
of
embeddings
According
to
this interpretation
of the
Brisson-Lienhardt theorem,
at any
time, each
"abstract"
z-cell
<fii
>
(d
1
}
is
assumed
to be
mapped
to a
"real"
i-Cel\d
ofPi(A):
It can be
observed
that
the
real
z-cell
fa(d] so
defined
is a
geometric object
embedded
in the
embedding space
M
m
of the
object
A. As a
consequence,
we
can
consider
that
fa (d)
defines
the
embedding
of d.
From
a
computer science point
of
view,
it is
convenient
to
define
(f>(d)
as
a
list
of
references
from
d to the
sorted list
{(/>o(cf),...,
(j>
n
(d)}
of
embed-
dings
defining
the
geometry
in
lR
m
of the
cells composing
the
Vertex
View
w
associated with
d:
For
this
purpose,
it is
necessary [22]
to
define
the
following
operators
on the
data
structures used
to
implement
the
GMaps:
•
setting
the
^-embedding
fa(d)
associated
with
a
given
Dart
d
•
getting
the
i-embedding
(/>i(d)
associated with
a
given
Dart
d
It
should
be
noted
that
the
embeddings
0
0
of
0-cells
are the
only
one
which
are
really mandatory
to
define.
If
needed,
all the
other
i-embeddings
can be
implicitly
deduced
from
the
embeddings
of the
0-cells;
for
this purpose,
we
only
have
to
proceed
as
follows:
1.
if a
cell
d =
4>i(d]
is a
simplex,
then
we can
interpolate
linearly
its i-
embedding
from
the
0-embedding
of its
vertices,
2.
otherwise,
we can
decompose
d
into simplexes
and
return
to
(1).
Consistency
of
embeddings
The
z-embedding
fa (d) of a
given Dart
d is
said
to be
consistent
if all the
Darts
of
the
abstract
i-cell
< fa > (d)
incident
d
share
the
same embedding
and if,
64
CHAPTER
2.
CELLULAR PARTITIONS
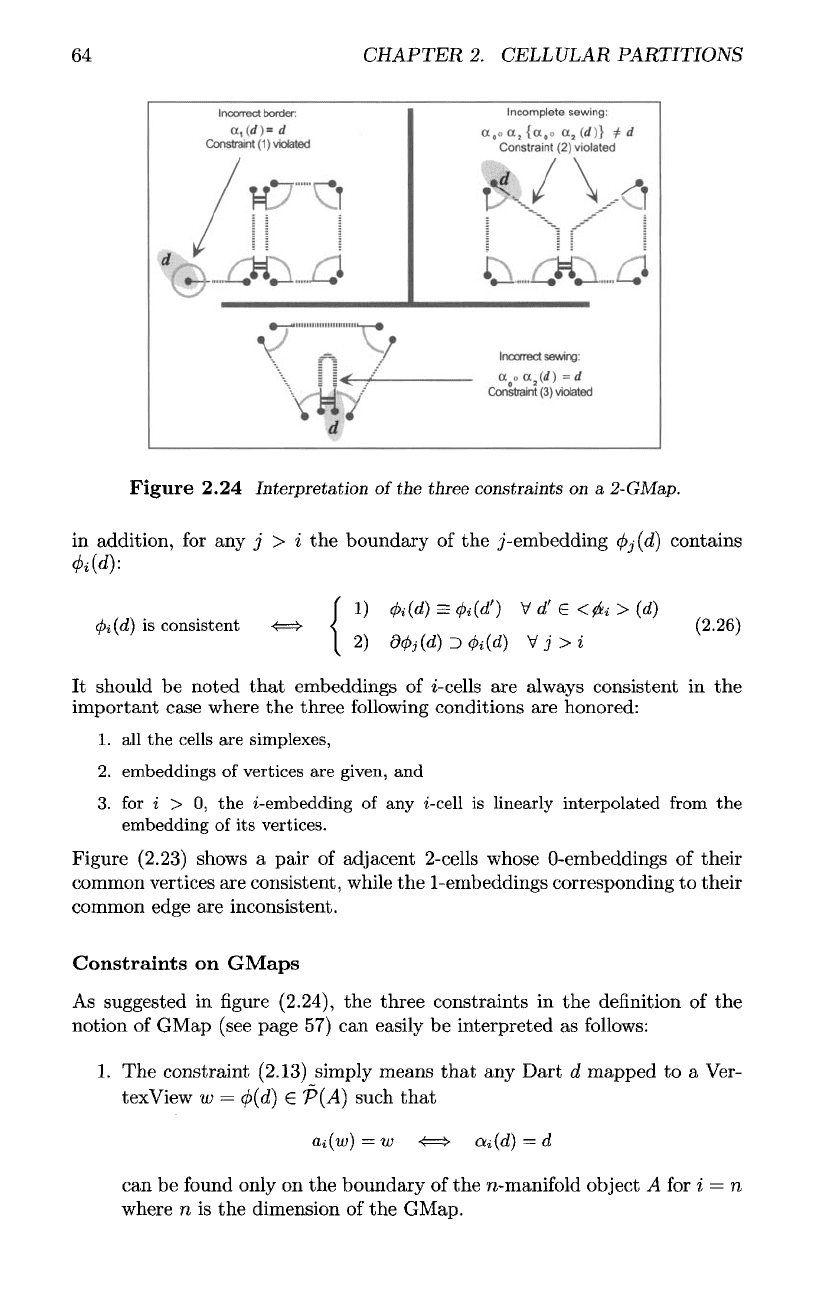
Figure
2.24
Interpretation
of
the
three constraints
on a
2-GMap.
in
addition,
for any
j'
> i the
boundary
of the
j-embedding
(f)j(d)
contains
&(d):
It
should
be
noted
that
embeddings
of
i-cells
are
always consistent
in the
important case where
the
three
following
conditions
are
honored:
1.
all the
cells
are
simplexes,
2.
embeddings
of
vertices
are
given,
and
3.
for i > 0, the
i-embedding
of any
i-cell
is
linearly interpolated
from
the
embedding
of its
vertices.
Figure
(2.23)
shows
a
pair
of
adjacent
2-cells
whose 0-embeddings
of
their
common
vertices
are
consistent,
while
the
1-embeddings
corresponding
to
their
common
edge
are
inconsistent.
Constraints
on
GMaps
As
suggested
in
figure
(2.24),
the
three constraints
in the
definition
of the
notion
of
GMap (see page
57) can
easily
be
interpreted
as
follows:
1.
The
constraint
(2.13) simply means
that
any
Dart
d
mapped
to a
Ver-
tex
View
w =
4>(d}
G
P(A)
such
that
can
be found
only
on the
boundary
of the
n-manifold
object
A for i = n
where
n is the
dimension
of the
GMap.

2.4.
2.
The
constraint
(2.14)
means
that
Vertex
Views
w
—
(f>(d)
of two
adjacent
cells
of
P(A)
must
be
completely "sewn"
by
involutions along their
common
boundary:
3.
The
constraint
(2.15)
means
that
Vertex
Views
w =
<j)(d)
incident
19
to a
same
cell
of
P(A)
cannot generate
"topological"
folds:
Discrete
model
M
p
(£li,Ni,(pi,C
Vi
)
associated
with
z-cells
To
any
n-GMap
G =
G(D,
0:0,
ai,...,
a
n
)
and for any
given integer
i
e
[0,
n],
it is
possible
to
associate
a set
0^
and an
operator
Nf
on
Oj
denned
by
In
other words,
Nf(k)
is the set of all the
abstract
i-cells
of G
"adjacent
to fc"
that
can be
reached
from
k in one
step
on G
corresponding
to an on
involution.
If
we
define
the
neighborhood
Ni(k]
of any
i-cell
k G
fij
as
follows
then
we can
build
a
discrete model
.M
p
(r^,
A^,
^,
C^J
where
(pi(k)
is a
vector
of
p
real values attached
to the
i-ce\\
k G
f^
while
C
(fi
is a set of
constraints
on the
function
<fn
denned
on
f^.
This considerably broadens
the
scope
of the
DSI
method introduced
in
chapter
1 and
fully
described
in
chapter
4. For
example,
if we
consider
a
2-GMap
associated with
a
surface
composed
of
polygonal adjacent
facets
as
the one
shown
in figure
(2.25)-A,
then:
• The
0-cells
correspond
to the
vertices
of
the
polygonal facets
and the set
No(k)
associated with
a
vertex
k
consists
of all the
vertices directly linked
to k by
an
edge
of
facet.
Any set of
attributes
</?o
defined
on
these
vertices
can be
interpolated
by DSI
using
the
model
M
p
(Qo,
NO,
(pOjC^g).
In
particular,
the
embedding
{<fo(k),(f>Q(k),ipQ(k)}
of any
vertex
k can be
interpolated
by
DSI.
Figure
(2.25)-B
gives
an
example
of
interpolation
of
<^o
on the
vertices
of a
surface
composed
of
polygonal facets.
• The
1-cells
correspond
to the
edges
of the
polygonal facets
and the set
N®(k)
associated with
an
edge
k
consists
of all the
edges sharing
a
vertex with
k.
Any
set of
attributes
(f\
defined
on
these
edges
can be
interpolated
by DSI
using
the
model
.M
p
(£2i,
A/i,
(^ijC^).
However, contrary
to the
case
of
0-cells,
it is not
possible
to
directly
use DSI for
modeling
the
embedding
of
1-cells.
Figure
(2.25)-C
gives
an
example
of
interpolation
of
(f>\
on the
edges
of a
surface
composed
of
polygonal facets.
19
See
definition (2.11).
GENERALIZED MAPS
65
66
CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.25 Examples
of
DSI
interpolations
on
i-cells
of
a
cellular partition
of
a
surface
(A)
composed
of
polygonal facets.
The
interpolated property
is
attached
to the
Q-cells
(vertices)
in
part (B),
to the
1-cells
(edges)
in
part
(C) and to
2-cells
(facets)
in
part (D).
The
values
of the
interpolated property
are
color
coded
and
vary
smoothly
from
an
i-cell
to its
neighboring i-cells.
• The
2-cells correspond
to the
polygonal facets themselves
and the set
N$(k)
associated with
a
facet
k
consists
of all the
facets sharing
an
edge with
k. Any
set of
attributes
<^2
defined
on
these facets
can be
interpolated
by DSI
using
the
model
A
/
t
p
(f^2,
A^,
<f>2,C<p
2
).
However, contrary
to the
case
of
0-cells,
it is
not
possible
to use DSI
directly
for
modeling
the
embedding
of
2-cells. Figure
(2.25)-D
gives
an
example
of
interpolation
of
</?2
on the
facets
of a
surface
composed
of
polygonal facets.
To
each
abstract
z-cell
k £
f^,
the
vectorial
function
(pi
defined
above
asso-
ciates
a
series
of p
values
which
can be
used
to
define
the
^-embedding
fa (d) of any
Dart
d
belonging
to
k.
Such
an
approach
is
widely
used
in
this
book
for
modeling
the
components
of
the
embeddings
corresponding
to the
geometry
and the
properties
of
objects
represented
by
discrete
models
(e.g.,
see
chapter
6).
2.4.3 "Magnetic" interpretation
of
Darts
Let
n
be a
strictly
positive
integer.
For any
n-GMap
G(D,
CKQ,
• •
-,
a
n
),
the set
of
Darts
D can
always
be
split
into
a
pair
of
"twin"
subsets
20
D
+
and D~ of
equal
size
and
such
that
20
It
should
be
noted
that
such
a
division
of D
into
two
subsets
is not
unique.
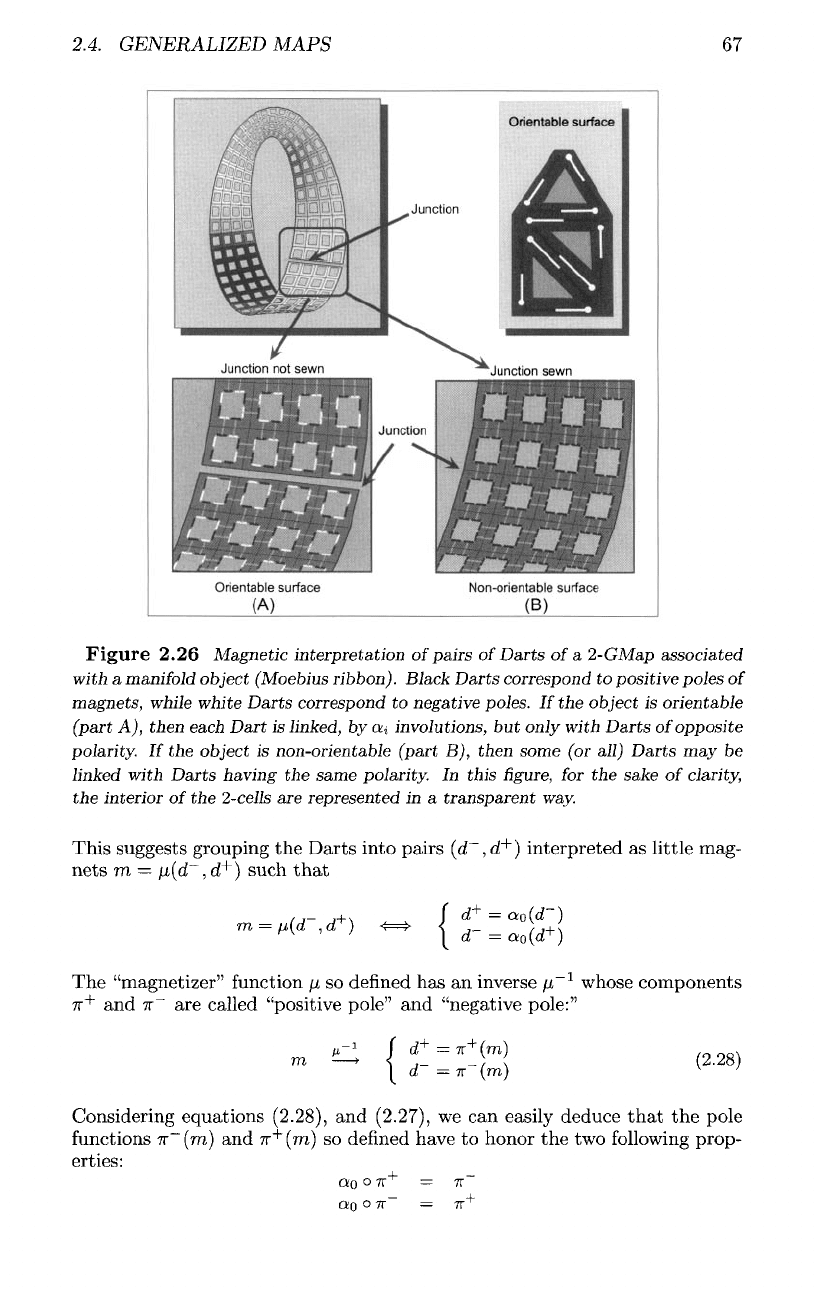
2.4.
GENERALIZED
MAPS
67
Figure
2.26 Magnetic interpretation
of
pairs
of
Darts
of
a
2-GMap associated
with
a
manifold
object (Moebius
ribbon).
Black Darts correspond
to
positive poles
of
magnets, while white Darts correspond
to
negative poles.
If
the
object
is
orientable
(part
A),
then each Dart
is
linked,
by
cn,i
involutions,
but
only with Darts
of
opposite
polarity.
If
the
object
is
non-orientable
(part
B),
then some
(or
all) Darts
may be
linked
with Darts having
the
same polarity.
In
this
figure, for the
sake
of
clarity,
the
interior
of the
2-cells
are
represented
in a
transparent way.
This
suggests
grouping
the
Darts
into
pairs
(d~~,
d
+
)
interpreted
as
little
mag-
nets
m
=
yu(rf~,
d
+
]
such
that
Considering
equations
(2.28),
and
(2.27),
we can
easily
deduce
that
the
pole
functions
TT~
(m) and
TT
+
(m) so
defined
have
to
honor
the two
following
prop-
erties:
The
"magnetizer"
function
JJL
so
defined
has an
inverse
fj,
1
whose
components
TT
+
and
TT~
are
called
"positive
pole"
and
"negative
pole:"
