Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


28
CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.1 An
example
showing
a
partition
of
the
subsurface
into
3D
regions
(cells)
bounded
by
horizons
and
faults
(surfaces).
notion
of
cellular model could provide
the
subject
of a
whole book. More
modestly,
in
this chapter,
we
present
without
any
proof
the
main concepts
and
properties
of
cellular models based
on the
notion
of
"Generalized-Maps"
also called
"GMaps"
initially introduced
in
geometric modeling
by
Lienhardt
[134,
137,
138].
It is
fair
to
mention
that
a
concept similar
and
equivalent
to
GMaps, called
"Cell-Tuple-Structure,"
was
independently proposed
by
Brisson
[35,
36,
37].
It is
also important
to
note
that
Computational Topology
is a
very active
field
of
research
and
many similar
or
different
approaches have been proposed
in
the
past
few
years
for
modeling
the
topology
of
complex objects.
For
example,
one
can
mention
the
pioneering work
of
Weiler [228]
and
also
the
recent works
of
Rossignac [179,
180, 182, 183, 184,
185].
and
Levy
[132].
This chapter
is
divided into
four
main sections:
• The first
section introduces
the
main concepts
of
mathematical topology.
• The
second
section
presents
the
notion
of
cellular
partition.
•
Then,
the
notion
of
GMaps,
an
algebraic
framework
used
to
model
cellular
partitions,
is
presented.
•
Last,
a
short
presentation
of how
GMaps
can be
used
to
implement
a
cellu-
lar
model
within
the
framework
of a
Computer-Aided
modeling
software
is
proposed.
2.2
Elements
of
topology
Topology
is a
branch
of
modern mathematics introduced
by
Poincare
in a
series
of
pioneering articles
[174, 175, 176]
published around
1900
to
study
the
properties
of
objects
that
are
preserved
through
deformations without
tearing
or
ripping.
In
this section,
the
basic definitions
and
notations used
in
the
following
sections
to
build
a
consistent representation
of
complex objects
are
introduced.

2.2.
ELEMENTS
OF
TOPOLOGY
29
Figure
2.2
An
example
of
geological cross section
partitioned
into
2D
regions
(cells)
bounded
by the
traces
of
horizons
and
faults.
2.2.1 Point set topology in ]Rn
The
introduction
of
this chapter clearly shows
the
central role played
by
"cells"
in
the
definition
of a
cellular topological model. From
a
mathematical point
of
view,
such cells
are
introduced
on
page
37 as
subsets
that
have
the
same
shape
as
open balls
defined
in
this section.
Open
and
closed
balls
Let n be a
positive integer
and let
11
•
11
be the
Euclidean norm
defined
on
M
n
.
By
definition:
An
open
n-ball,
or
more simply,
an
open ball
in
M
n
with center
XQ
o
and
radius
p > 0
consists
of the set
B™(XQ)
of
points
x 6
JR
n
located
at
a
distance always shorter than
p
from
XQ:
A
closed
n-ball
in
lR
n
with center
XQ
and
radius
p > 0
consists
of th
set
B™(XQ)
of
points
x G
M
n
located
at a
distance always shorter
or
equal
to p
from
XQ:
An
n-sphere
in
IR
n
with center
XQ
and
radius
p > 0
consists
of the set
8B™(xo)
of
points
x G
JR
n
located
at a
distance strictly equal
to p
from
A

30
CHAPTER
2.
CELLULAR PARTITIONS
It is
obvious
that
We
will
say
that
In
the
particular case where
n = 0, by
convention,
one
defines:
Examples
of
n-balls
are
shown
on the
left-hand
side
of figure
(2.5).
Open
and
closed
sets
Let
A
be a
subset belonging
to
M
n
.
We
will
say
that
o
• A is an
open
set if, for
each
x
e
A,
there
is an
open ball
B™(x)
fully
contained
in A:
The
family
O(lR
n
)
of all the
open sets
of
]R
n
verifies
the
following
prop-
erties:
01
:
IR
n
and 0 are
open
sets.
02 : Any
union
of
open
sets
is an
open set.
03 : Any finite
intersection
of
open
sets
is an
open set.
• A is a
closed
set if it is the
complement
of an
open set:
The
family
]C(M
n
)
of all the
closed sets
of
M
n
verifies
the
following
properties:
/Ci
:
M
n
and 0 are
closed
sets.
K.2
'•
Any finite
union
of
closed
sets
is a
closed set.
/Ca
: Any
intersection
of
closed
sets
is a
closed set.
In
particular,
a set
consisting
of one
isolated point
is a
closed set.
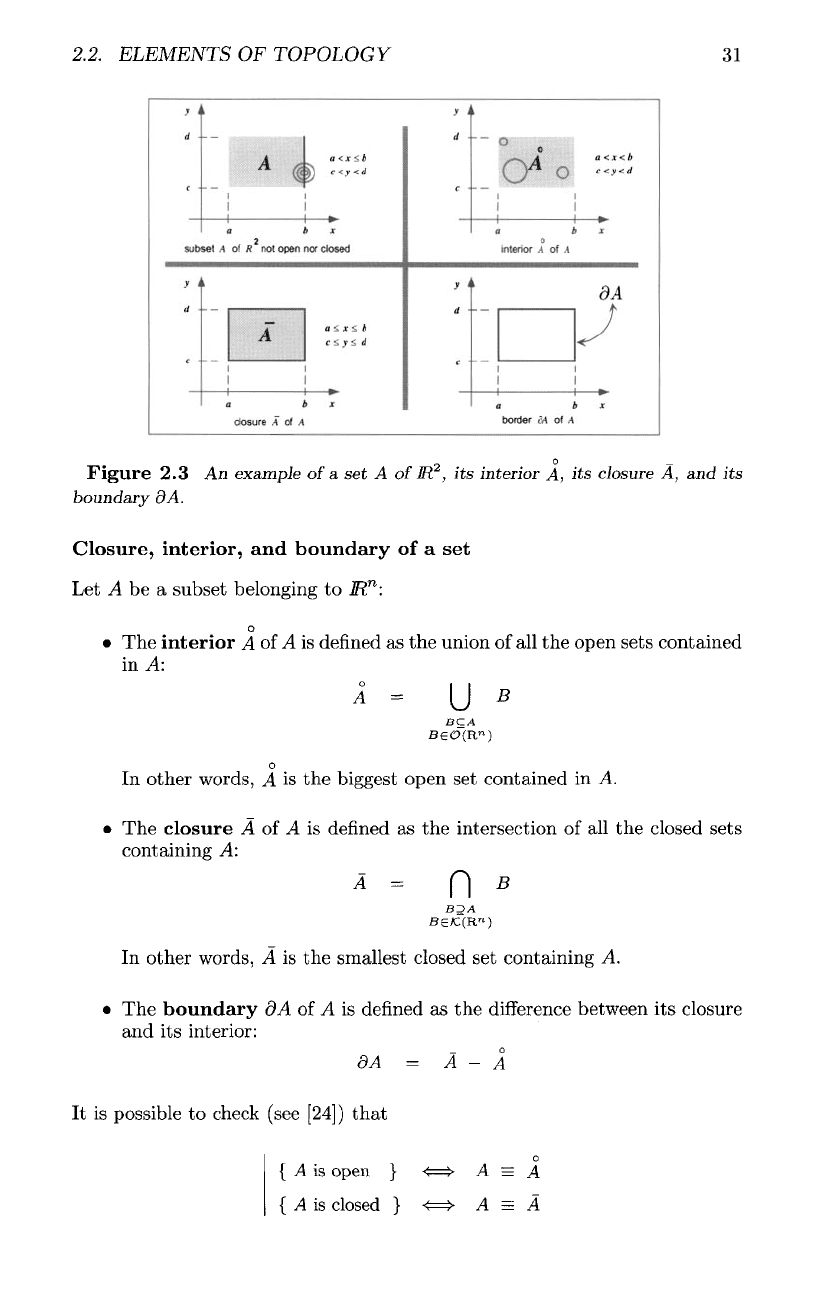
2.2. ELEMENTS
OF
TOPOLOGY
31
Figure
2.3 An
example
of
a set A
of
1R
2
,
its
interior
A, its
closure
A, and its
boundary
dA.
Closure,
interior,
and
boundary
of a set
Let
A be a
subset belonging
to
JR
n
:
o
• The
interior
A of A is
defined
as the
union
of all the
open sets contained
in
A:
o
In
other words,
A is the
biggest open
set
contained
in A.
The
closure
A of A is
defined
as the
intersection
of all the
closed sets
containing
A:
In
other words,
A is the
smallest closed
set
containing
A.
The
boundary
dA of A is
defined
as the
difference
between
its
closure
and its
interior:
It is
possible
to
check (see
[24])
that

32
CHAPTER
2.
CELLULAR PARTITIONS
Example
o
For
instance,
one can
check
that
the set A
shown
in figure
(2.3)
and
defined
by
is
an
open
set of
M
2
.
However,
if one of the
strict
inequalities,
say x < b
is
replaced
by x
<
6,
then
the
corresponding
set A is no
longer
an
open
set
and is not a
closed set:
this
is due to the
fact
that
no
open ball with center
(6,
(d
+
c)/2),
which belongs
to the set A, can be
contained
in A.
2.2.2
Generalization
to
non-Euclidean spaces
The
notion
of
topological space [24, 105, 158]
defined
in
this section general-
izes
to any set E the
topological notions presented
in the
previous section
in
the
particular case where
E =
lR
n
.
Moreover,
the
notion
of
"neighborhood,"
which
is the key
element used
to
define
the
important notion
of
"homeomor-
phism,"
(see page
34) is
introduced.
Definitions
1:
Notion
of
topological
space
Let
E be a set and let
O(E]
be a
family
of
parts
of E
verifying
the
following
properties:
O\
:
the set E and the
empty
set 0
belong
to
O(E}\
O-2
:
any
union
of
elements
of
O(E)
is an
element
of
O(E};
Os
:
any
finite
intersection
of
elements
of
O(E)
is an
element
of
O(E);
By
definition:
The
pair
(E,
O(E))
is
called
a
"topological
space."
• Any
element
of E is
called
a
"point"
of E.
• Any
element
of
O(E)
is
called
an
"open
subset"
of E.
• Any
part
of E
that
is the
complement
of an
open
subset
of E is
called
a
"closed
subset"
of
E.
Both
E and 0 are
closed
subsets.
Moreover:
o
• The
interior
A of a
subset
A of E is
defined
as the
union
of all the
open
subsets
contained
in A.
• The
closure
A of a
subset
A of E is
denned
as the
intersection
of all the
closed
subsets
of E
containing
A.
_ o
• The
boundary
dA of a
subset
A of E is
denned
as the
difference
(A— A)
•
Definition
2:
Notion
of
neighborhood
Let
(E,O(E}}
be a
given topological space.
For any
point
x of
E,
we
call
"neighborhood"
of x any
open subset N(x)
of E
containing
the
point
x:

2.2.
ELEMENTS
OF
TOPOLOGY
33
It can be
observed
that
this notion
of
neighborhood generalizes
to
topological
spaces
the
notion
of
open
n-ball
denned
for the
Euclidean space
lR
n
.
In the
following,
for the
sake
of
consistency
lR
n
will
be
associated
implicitly with
the
topological space
(M
n
,O(lR
n
}}
where
O(lR
n
}}
is the
family
of all the
open
subsets
of
M
n
.
2.2.3
Transformation
(or
mapping)
From
an
intuitive standpoint, topology
can be
viewed
as the
science
of ob-
jects made
of
plasticine whose geometry
can
change continuously (without
any
tearing) while preserving
the
global shape. Such transformations called
"homeomorphisms"
or
"topological transformations," which play
a
central
role
in
this
chapter,
are
introduced
in
this section.
Definition
Let
(E,
O(E}}
and (F,
O(F}}
be two
topological spaces
and let D be a
subset
of
E. A
rule
T
that
associates
an
element
y E F
with every element
x
e
D is
said
to be a
"transformation"
or a
"mapping"
from
E to F
with domain
D:
The
image
T(D)
of
D by T is
denned
by
By
definition,
T is
"one-to-one"
if, to any
point
y
6
T(D),
there
is
only
one
corresponding point
x in D:
Moreover,
in the
case where
T is
one-to-one, there
is an
inverse transformation
noted
as
T
-1
and
defined
by
In
other words,
we
have:
Continuity:
The
case
of
Euclidean
spaces
Let
T be a
transformation
from
D
C
]R
n
to
JR
m
.
By
definition,
we
will
say
that
• T is
continuous
at x
G
D if, for any
given
e
> 0,
there
exists
a
6(e)
> 0
such
that
• T is
continuous
on D if it is
continuous
for any
point
x G D.
In
other words,
T is
continuous
at x if
points arbitrarily close
to y =
T(x)
are
images
of
points
sufficiently
close
to x.

34
CHAPTER
2.
CELLULAR PARTITIONS
Continuity:
The
general
case
The
definition
of the
notion
of
continuity introduced above
is
extended
as
follows
to any
pair
of
topological spaces
(E,
O(E}}
and (F,
O(F}}:
Let
T be a
transformation
from
D C E to
F.
By
definition:
• T is
continuous
at x G D if, for any
neighborhood
N(T(x))
of
T(x)
G F,
there
exists
a
neighborhood
N(x)
of
x
£
E
such
that
• T is
continuous
on D if it is
continuous
for any
point
x
E
D.
It can be
shown (see [24,
141])
that
o
• T is
continuous
on D if, and
only
if, the
inverse image
T~
(A) of any
open
o
subset
AG
T(D)
is an
open subset
of
D.
• T is
continuous
on D if, and
only
if, the
inverse image
T~
l
(A)
of any
closed
subset
A G
T(D)
is a
closed subset
of
D.
Homeomorphism
If
a
transformation
T
from
D C E to F is
continuous
and
one-to-one, then
T"
1
exists.
If,
moreover,
T~
l
is
also continuous, then
T is
said
to be a
"homeomorphism"
and the
sets
D and
T(D)
are
said
to be
"homeomorphic"
or
"topologically
equivalent."
It can be
observed
that,
if T is a
homeomorphism, then
where
M(x)
and
A/"(y)
are the
families
of the
neighborhoods
of x and y,
respectively.
Local
topological
dimension
of a set
Let
(E,O(E))
be a
topological space.
The
local topological dimension
d(x)
o
of
a
subset
A of E is
defined
at any
point
x
6^4
as the
largest nonnegative
integer
n
such
that
there
is, at
least,
one
neighborhood
N(x)
of x
such
that
N(x]
H
A is
homeomorphic
to an
open
n-ball:
For
example,
in the
case where
A is a
subset
of E
=
7R
3
:
• if A
reduces
to a
single
point
x,
then
d(x)
= 0;
o
• if A is a
curve,
then
d(x)
=
I
for any
point
x
€A',
o
• if A is a
surface,
then
d(x)
= 2 for any
point
x
£A]
o
• if A is a
volume, then
d(x)
— 3 for any
point
x
EA-
Note
that
the
local dimension d(x)
can be
undefined
if no
neighborhood
of
o
x
GA
can be
found
homeomorphic
to an
open ball
(e.g.,
see figure
(2.4)-B).

2.2. ELEMENTS
OF
TOPOLOGY
35
2.2.4
Objects
The
cellular paradigm presented
in the
introduction
of
this chapter relies
on
an
analogy with "biological objects."
It
should
be
noted
that
the
skin
of
any
biological object belongs
to
this object; this
is at the
origin
of the
mathematical
definition
of the
notion
of
object proposed
in
this section.
Manifold
and
non-manifold
objects
Let
(E,
O(E})
be a
topological space such
that,
for any
pair
of
distinct points
x\
and
#2
of
E,
there exists neighborhoods
N(XI)
and
N(x^)
such
that
1
N(XI]
n
N(x2]
= 0. In
such
a
case,
by
definition
we
will
say
that
a
subset
A
of
E is an
object
embedded
in E if A is
closed:
Moreover,
we
will
say
that
An
object
A is
"n-manifold"
or,
more simply, "manifold,"
if its
local
dimension
can be
defined,
it is
constant
and it is
equal
to n for any
o
point
x
£A'-
In
such
a
case,
n is
called
the
"dimension"
of A:
Conversely,
an
object
A is
said
to be
"non-manifold"
if its
local
dimen-
o
o
sion
is not
constant
on A or
cannot
be
defined
in
some
parts
of
A'-
Examples
of
manifold
and
non-manifold
objects
Figures
(2.6),
and
(2.12)
give some examples
of
2-manifold
objects embedded
in
E
=
JR
3
,
while examples
of
non-manifold objects
are
shown
in figure
(2.4).
As
a
tutorial,
figures
(2.4)-A
and
(2.4)-B
are
used
to
explain
why the
object
A
consisting
of
three rectangles
of
7R
3
sharing
a
common
edge
2
C
constitutes
o
a
non-manifold object.
For
this purpose,
for any
point
x
GA,
let us
define
o
B
p
(x]
as
being
the
intersection
of A
with
an
open
3-ball
centered
on x:
With such
a
definition
of
B
p
(x},
one can
observe
that
^uch
a
topological
space
is
called
a
"Hausdorff"
space;
for
example,
E
=
]R
n
is a
Hausdorff
space.
2
Such
an
edge
is
called
a
"radial
edge"
[228]
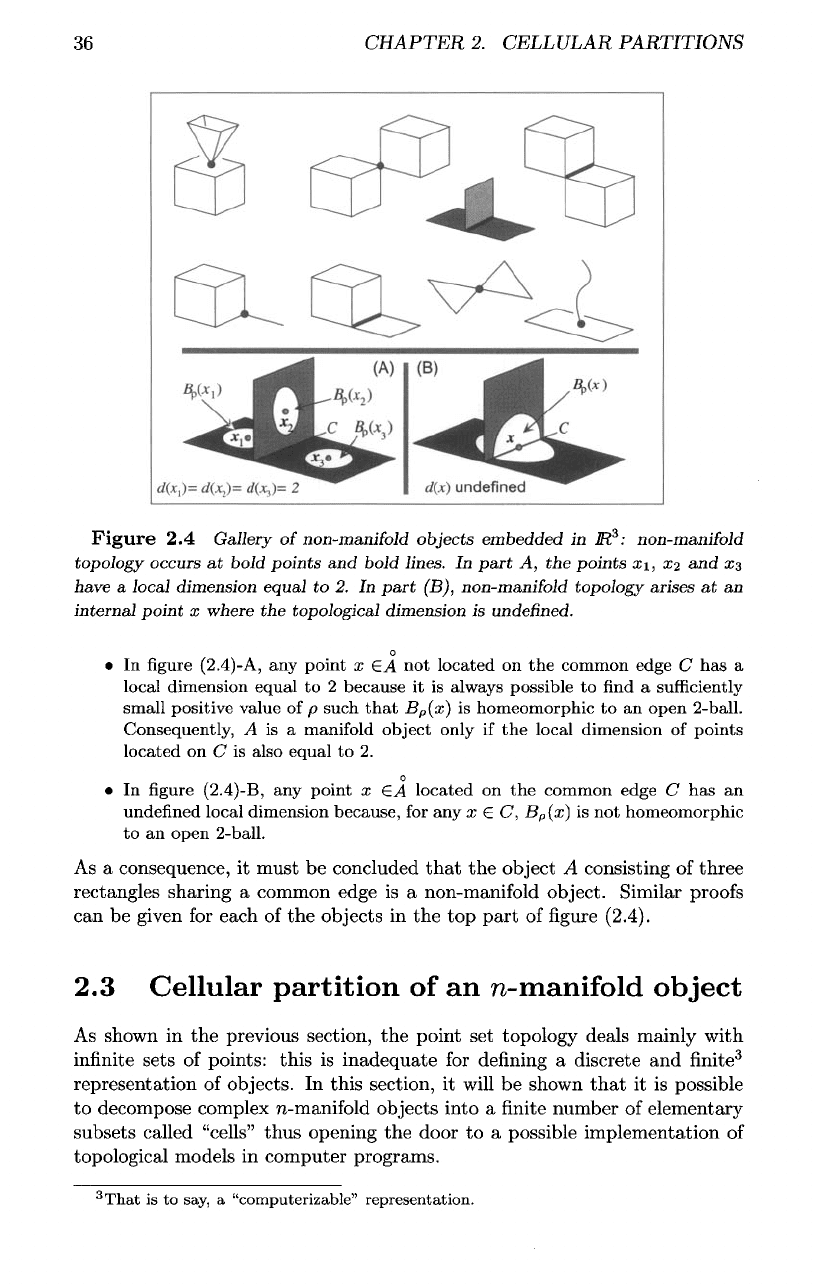
36
CHAPTER
2.
CELLULAR
PARTITIONS
Figure
2.4
Gallery
of
non-manifold objects embedded
in
1R
3
:
non-manifold
topology occurs
at
bold
points
and
bold lines.
In
part
A, the
points
Xi,
X2 and
xz
have
a
local dimension equal
to 2. In
part
(B), non-manifold topology arises
at an
internal
point
x
where
the
topological dimension
is
undefined.
o
• In
figure
(2.4)-A,
any
point
x
GA
not
located
on the
common edge
C has a
local
dimension
equal
to 2
because
it is
always
possible
to find a
sufficiently
small
positive
value
of p
such
that
B
p
(x)
is
homeomorphic
to an
open
2-ball.
Consequently,
A
is a
manifold object only
if the
local dimension
of
points
located
on C is
also
equal
to 2.
o
• In figure
(2.4)-B,
any
point
x
£A
located
on the
common edge
C has an
undefined
local dimension because,
for any x €
C,
B
p
(x]
is not
homeomorphic
to an
open 2-ball.
As
a
consequence,
it
must
be
concluded
that
the
object
A
consisting
of
three
rectangles sharing
a
common edge
is a
non-manifold
object. Similar
proofs
can be
given
for
each
of the
objects
in the top
part
of figure
(2.4).
2.3
Cellular
partition
of an
n-manifold
object
As
shown
in the
previous section,
the
point
set
topology deals mainly with
infinite
sets
of
points: this
is
inadequate
for
defining
a
discrete
and finite
3
representation
of
objects.
In
this section,
it
will
be
shown
that
it is
possible
to
decompose complex
n-manifold
objects into
a finite
number
of
elementary
subsets called "cells" thus opening
the
door
to a
possible implementation
of
topological
models
in
computer programs.
3
That
is to
say,
a
"computerizable"
representation.
2.3.
CELLULAR PARTITION
OF AN
N-MANIFOLD
OBJECT
37
Figure
2.5
n-cells
embedded
in
1R
3
are
homeomorphic
to
open
n-balls.
2.3.1
Notion
of
n-cell
Definition
Let
C be an
open
subset
of
JR
m
.
By
definition,
we
will
say
that
C is an
"n-cell" embedded
in
M
m
or,
more simply,
a
"cell"
if C is
homeomorphic
to
an
open
n-ball:
Examples
Figure
(2.5)
shows some examples
of
n-cells embedded
in
H
3
:
• a
0-cell
is an
isolated point
in
J?
3
;
• a
1-cell
is a
simply connected
(i.e.,
in one
piece) curve
in
JR
3
whose
two end
points have been removed;
