Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


CHAPTER
2.
CELLULAR PARTITIONS
Figure
2.32 Radial junction
of
three
surfaces
along
a
common
edge
contribut-
ing to a
partition
P(A)
of
a
3-manifold
"universe"
object
A
(not
represented).
The
cellular
partition induces
a
3-GMap where
the
links between
surfaces
along
the
com-
mon
edge
are
modeled
by
0:3
and
0:3
involutions. Each
oti
involution
is
represented
by i
parallel
segments
(Q>Q
are not
shown).
The
Darts belonging
to
free
edges
are
characterized
by
0:3
(of)
=
0:2(d),
and,
in
this
case,
only
as
links
are
represented.
It can be
observed
that,
the
cellular partition
P(M
n+1
)
associated with
the
Frame
F(W)
of W can
always
be
chosen
in
such
a way
that
•
F
+
(W)
is
isomorphic
to
dL'(W)
•
F~(W)
is
isomorphic
to
8L'(W)
In
other words,
as
figure
(2.31) shows
and as
suggested
by
Levy
[132],
it is
always
possible
to
define
a
function
cr
FL
associating each Dart
d G
(D~p(jDj,}
of
the
frame
F(W) with
a
Dart
d €
D'
L
of the
"simplified" version
dL'(W)
of
the
boundary
of
L(W):
In
a
certain
sense,
it can be
said
that
this
function
a
FL
allows
a
Frame
to
"delegate"
its
embedding
to a
Lattice.
Notions
of
Model
and
Region
Let
{Wi,...,
WN}
be a set of
n-Dividing-Walls
embedded
in the
JR
n+1
space
such
that
By
definition,
for any
cellular partition
P(]R
n+l
}
honoring
the
following
con-
straints
we
will
say
that
2.5.
IMPLEMENTING GMAP-BASED MODELS
89
• the
(n
+
l)-cells
of
M(Wi,...,
W
N
)
are the
"Regions"
of
M(Wi,...,
W
N
).
An
illustration
of
these notions
of
Dividing-Walls,
Model,
and
Regions
can be
found
in
figure
(2.30).
2.5.4
Operations
on a
Model
If
our
purpose
is to
build
3D or 2D
geological models such
as
those represented
in
figures
(2.1),
and
(2.2) interactively, then
we
need
to
have
a
tool
for
"gluing"
a
free
Edge
of an
n-Dividing-Wall
(horizon
or
fault)
to an
Edge
of
another
n-
Dividing-Wall.
As
shown
in
figures
(2.32),
and
(2.17),
from
a
topological point
of
view,
these
n-Dividing-Walls
are
represented
in the
lR
n+
embedding space
by
their Frames,
and the
gluing operation corresponds
to the
installation
of
a
n
links between
the
Edges
of
these Frames
(see
figures
(2.32),
and
(2.33)).
In
this section,
we
present this fundamental operation
and its
inverse, with
other
lesser
operations
- all
very
useful
in
practical
applications.
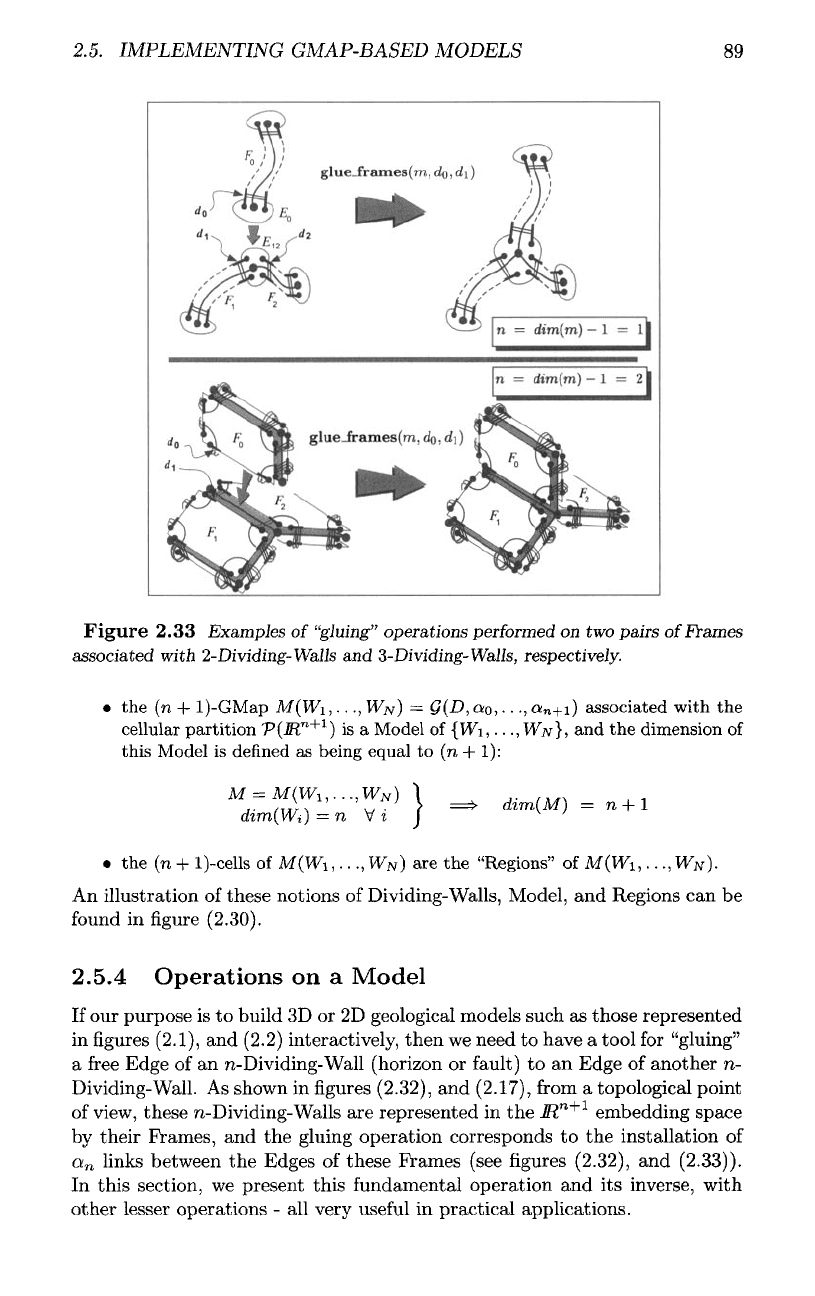
Figure
2.33
Examples
of
"gluing"
operations
performed
on two
pairs
of
Frames
associated
with
2-Dividing-Walls
and
3-Dividing-Walls,
respectively.
• the (n +
l)-GMap
M(Wi,...,
WN)
=
G(D,
ao,...,
a
n
+i)
associated
with
the
cellular
partition
P(JR
n+l
)
is a
Model
of
{Wi,...,
WN},
and the
dimension
of
this
Model
is
defined
as
being
equal
to (n +
I):

90
CHAPTER
2.
CELLULAR PARTITIONS
Gluing
and
ungluing
Frames
The
most important operations
on a
Model
are
gluing
and
ungluing
of
Frames
associated with
n-Dividing-Walls;
as
suggested
in
figures
(2.32),
and
(2.33):
•
glue_frames(m,
do,di)
glues,
in a
"non-manifold"
way,
a
Frame
FQ
of
the
Model
m
"between"
two
adjacent
Frames
{Fi,F%}
of ra. If we
note
the
dimension
of the
Dividing-Walls
of m,
then
the
Frames
FQ,
F\
and
F-2
are
assumed
to
contain, respectively,
the
Darts
(do,
^1,^2),
such
that
The
gluing operation consists
of
"inserting"
FQ
"between"
(Fi,F
2
)
very
like
a new
page between
two
existing pages
of a
book. Such gluing
is
performed
along
a
common "edge"
E\<2
shared
by
(F\,F<2)
and an
edge
EQ
of
FQ
such
that
—
Ei2
is the (n
—
l)-cell
incident
to
d\
and
cfo,
and
—
EQ
is the (n —
l)-cell
incident
to do.
This gluing operation
is
only possible
if do
honors
the
following
precon-
dition,
specifying
that
do is
free:
37
If
this precondition
is
honored, then
the
gluing operation
is
performed
as
follows:
1.
Discard
(do not
remove)
the
embeddings
of all the
z-cells
incident
to do
for
i
<
(n
—
1).
2.
Add
din
involutions
between
the
pairs
of
Darts
(do,di)
and the
pair
of
Darts
(a^
+1
(d
0
),d
2
).
3.
Add all the
ctf
involutions
between
the
Darts
necessary
to
honor
the
constraints
(2.13), (2.14),
and
(2.15).
4. For any
Dart
<5i
belonging
to the (n
—
l)-cell
containing
do,
assign
the
same
embedding
as do to
6\.
It
should
be
noted
that
—
Starting
the
gluing
operation
by
linking
the two
pairs
of
given
Darts
(do,di)
and
(a^
+1
(do),d2)
by an
a^
involutions
fully
defines
the
"direc-
tion"
of the
gluing.
37
If
a^(do)
and
a
n
°
&n+i(do)
belong
to the
same virtual
cell,
then
do
should also
be
considered
as
free.
In
practice,
the
gluing operation must
be
slightly
modified
to
take care
of
this special case.

2.5.
IMPLEMENTING GMAP-BASED MODELS
91
—
It is
always possible
to
have
d<2
=
o£
+
i(di).
In
this case,
F\
=
F<2
and
the
gluing operation
is
very similar
to a
sewing operation except
that
we
are
"sewing"
two
Frames,
FQ
and
FI
=
F?.
•
unglue_frame(m,
d)
unglues
the
Frame
F
incident
to a
given
Dart
d
in
the
Model
m.
If we
note
the
dimension
of the
Dividing-Walls
of m,
then this operation
is
per-
formed
without
any
preconditions,
as
follows:
1.
Restore
an
a^
involution between
the two
Darts
d and
o;^
+1
(d).
2.
For all the
Darts
that
were initially contained
in the
same
(n —
l)-cell
as d. add all the
a^+i
involutions necessary
to
honor
the
constraints
(2.13),
(2.14)
and
(2.15).
It
should
be
noted
that
the
glue-frames
() and
imglue_frame()
operations
are not
neutral relative
to the
regions
of the
model:
1.
glue_frames(m,
do,
d\)
can
kill
a
region containing
the
Dividing-Walls
asso-
ciated
with
the
Frames
to be
glued
and
replace
it by two new
regions located
on
both sides
of
these
Frames.
2.
unglue_frame(m,
d) can
kill
the two
regions located
on
both
sides
of the
Dividing-Walls
associated
with
the
Frames
to be
unglued
and
replace
them
by a new
region resulting
from
the
union
of the two
killed regions.
This means
that,
as a
side
effect,
these
two
operations
may
modify
the
list
of
regions
associated
with
the
Model
m.
Other
operations
Among
the
many
other
operations
that
can be
defined
on an
n-Model,
we can
mention:
•
Addition
of a new
Frame
to a
Model.
This
allows
the
number
of
"Dividing-
Walls" contributing
to the
partition
of the
object associated with
the
Model
to be
modified incrementally.
•
Removal
of an
existing Frame
from
a
Model.
As a
side
effect,
this
operation
can
modify
the
model's list
of
regions.
•
Retrieving
the
region
of a
Model containing
a
given point.
•
Retrieving
all the
Frames
of a
Model surrounding
a
given region.
•
Cutting
the
cells
of a
Model
by a new
n-Dividing-Wall.
Comment
about
virtual
cells
As
shown
in
figure
(2.17),
we
have been
led to
introduce "virtual" cells
in
Models
to
take into account
the
case where
a
region
is
fully
included
in
another
region.
We
have already mentioned
that
the
virtual cells
do not
need
to
have
embeddings,
and
this
is
relevant
as
long
as we do not
perform
a cut
operation
of
a
Model
by a new
Dividing-Wall.
For
example,
if we
want
to cut the
cells
of
the
two-dimensional Model shown
in
figure
(2.17)
by a
curve
(1-Dividing-
Wall)
intersecting
the
virtual
1-cell,
then

92
CHAPTER
2.
CELLULAR
PARTITIONS
• we
actually
must
know
the
embedding
of the
virtual
cell,
and
• the
virtual
cell
has to be
partitioned
to
take
into
account
its
points
of
inter-
section
with
the
cutting
curve.
Such
an
approach
is too
heavy
and
ineffective.
A
better approach consists
of
maintaining
a
tree
that
describes
the
inclusion relationships
of the
regions
within
the
Model
and
proceeding
as
follows:
1.
"Prepare"
the
Model
to be cut by
removing
all the
virtual
cells.
2.
Perform
the cut
operation.
3.
Use the
inclusion
relationships
between
the new
regions
for
installing
new
virtual
cells
connecting
the
boundary
of a
region
to the
boundary
of
each
of
its
subregions.
Note
that
operation
(1)
temporarily transforms
the
GMap corresponding
to
the
Model into
a
graph
that
is not a
GMap,
but,
from
a
practical point
of
view,
this
does
not
matter.
Note also
that
the
operation
(3) is
also
in
charge
of
re-establishing
the
Model
in a
state
compatible with
the
definition
of the
notion
of
GMap.
Incremental
construction
of a
Model
In
practice,
the
operations presented above
are
used
for the
incremental build-
ing
of a
Model
as
follows:
1.
Create
an
empty
(n +
1}
dimensional Model
M
=
M(0).
2.
Create
a
Lattice
L(W]
corresponding
to a
cellular
partition
P(W)
of a
n-Dividing-Wall
W.
For
this purpose
it is
possible
to
proceed
as
follows:
(a)
create
an
empty
n-GMap
L(W),
(b)
use the
micro
transformations
{tj}
or the
create_cell() macro
transfor-
mation
described
on
pages
74 and 77 for
building
isolated
n-cells
and
add
them
to
L(W),
and
(c)
if
needed,
use the sew
operator
described
on
page
77 to
weld
some
n-cells
of
L(W}.
3.
Create
a
Frame
F(W]
such
that
L(W)
is a
Lattice
of
F(W}
and add
W to the
current Model
M.
4.
If
necessary, repeat operations
(2) and (3) for a
series
of
n-Dividing-
Walls
{Wi,...,
W
N
}
leading
to M =
M(W^...,
W
N
).
5.
If
necessary,
use the
glue
operator
to
weld some
Dividing-Walls
of the
Model
M(Wi,...,W
N
).
As
can be
seen,
in
this
approach,
the
"sew"
and
"glue" operators
perform
complementary
roles:
• The sew
operator
is
used
to
weld
a
pair
of
n-cells
of a
Lattice.
• The
glue
operator
is
used
to
weld
a
pair
of
Frames.
2.6. CONCLUSIONS
93
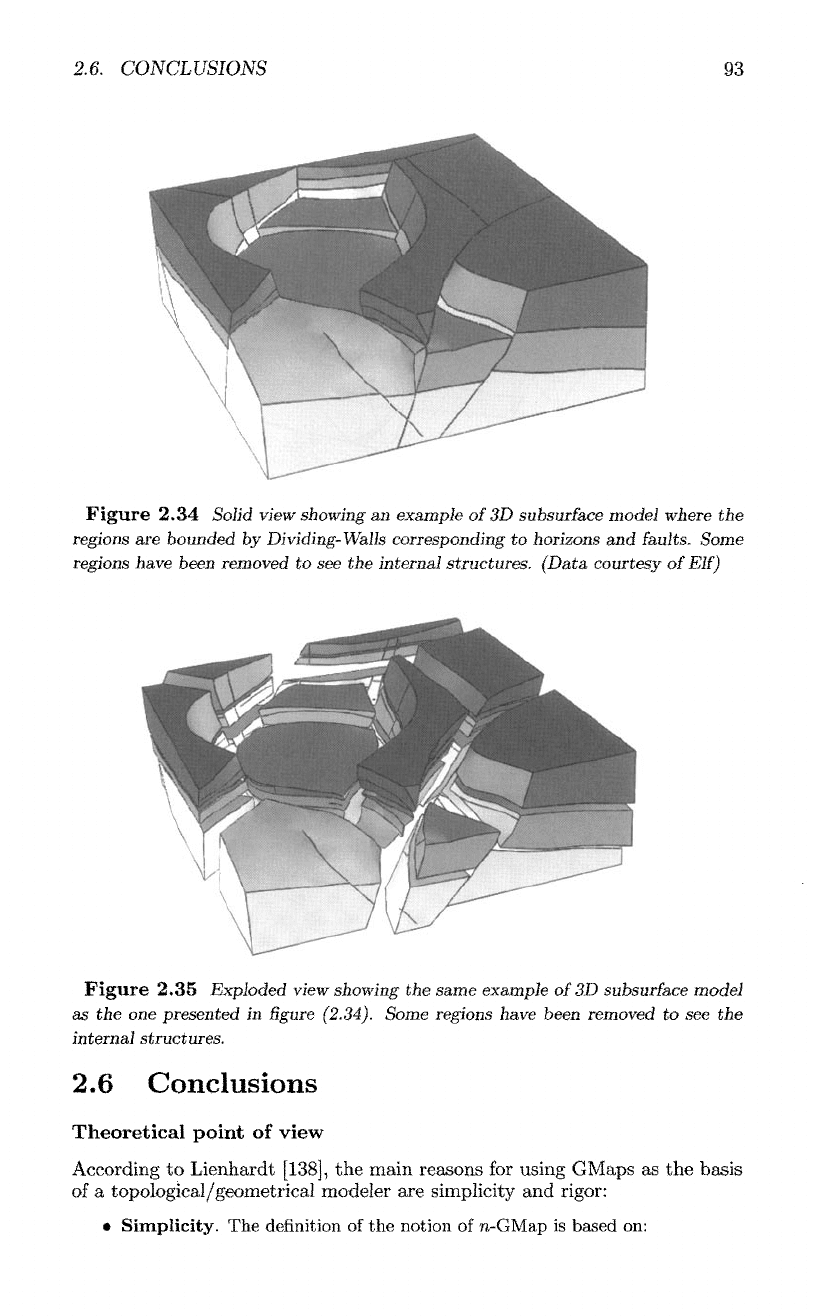
Figure 2.34
Solid view showing
an
example
of
3D
subsurface
model where
the
regions
are
bounded
by
Dividing-Walls
corresponding
to
horizons
and
faults. Some
regions
have been removed
to see the
internal structures. (Data courtesy
of
Elf)
Figure 2.35
Exploded view showing
the
same example
of
3D
subsurface
model
as
the one
presented
in figure
(2.34).
Some regions have been removed
to see the
internal structures.
2.6
Conclusions
Theoretical
point
of
view
According
to
Lienhardt
[138],
the
main
reasons
for
using
GMaps
as the
basis
of
a
topological/geometrical
modeler
are
simplicity
and
rigor:
•
Simplicity.
The
definition
of the
notion
of
n-GMap
is
based
on:

94
Figure
2.36
Wireframe
representation
of the
Frames
of the
Dividing-Walls
corresponding
to the 3D
subsurface
model presented
in figure
(2.34).
one
single
data
type:
the
Dart,
and
—
one
single
type
of
operator:
the
involution.
•
Rigor.
It is
well
known
that
controlling
the
construction
of a
geometric
object
and
avoiding topological inconsistencies
are key
issues
in
geometric
modeling.
At any
time,
the
topological properties
of a
cellular partition
P(A)
of
an
n-manifold
object
A can be
algebraically computed
and
controlled
on
the
associated
"abstract"
n-GMap.
This
can be
extremely
useful
during
the
construction process, since
it
enables
us to
predict
the
result
of
transforma-
tions.
As a
consequence,
it is
possible
to
control
a
priori [138]
the
consistency
of
these transformations.
From
a
programming
point
of
view
[23],
these
two
properties
of
GMaps
make
them
an
excellent
choice
for
developing
a
topological/geometrical
modeler:
• The
source code
of a
modeler based
on the
notion
of
GMap
can be
extremely
concise:
for
example,
the
kernel
of the
modeler implemented
in the
gOcad
software
comprises less than 1500 lines
of C++
source code [132,
52].
•
Response time
is
comparable with those
of
commercial products with similar
features
[23]
and may be
even better.
For
example,
the
main operations,
particularly
the
traversals,
have
a
time complexity
of
O(\D\),
where
\D\ is the
number
of
Darts. This
is not the
case
for
many commercial modelers
who
often
take
O(\D\
2
)
due to
their
lack
of
directly
accessible
topological
data.
•
Other classic data structures, such
as
those derived
from
the
well-known
"winged edge" [16,
17,
152]
or
"radial
edge"
[228],
often
take
up
compara-
ble
memory space
for a
more restricted modeling area.
• Due to the
algebraic nature
of the
notion
of
GMap,
it is
possible
to
test
the
consistency
of the
software
by
Algebraic Specification techniques
[23].
Such
an
approach
is
impossible
with
models
based
primarily
on
data
structures
rather
than
on
algebraic
properties.
CHAPTER 2. CELLULAR PARTITIONS
94

2.6.
CONCLUSIONS
Practica l point
of
view
For
software
developers,
the
following
strengths
of
GMaps
can be
mentioned:
•
There
are
only
two
main concepts
to
understand: Darts
and
involutions.
•
There
is a
clear
uncoupling
of
—
the
topology
from
attributes,
and
—
the
dimension
of the
objects
from
the
dimension
of the
embedding space.
•
Last
but not
least,
from
a
programming
point
of
view
it is
possible
to de-
fine
a
concise Application Programming Interface (API) based
on the
GMaps
mathematical model.
For
geologists,
GMaps
provide
a
consistent
framework
to
decompose
the
sub-
surface
into
homogeneous
regions
corresponding
to
3-cells.
In
practice,
as
suggested
in figures
(2.1), (2.34), (2.35),
and
(2.36),
the
most
natural
parti-
tion
consists
of
identifying
these
regions
with
the
layers
and
fault
blocks.
95
This page intentionally left blank

Chapter
3
Tessellations
In
computational
geometry,
"tessellation"
refers
to any
method allowing
the
partitioning
of
a
polyhedral
n-dimensional
object into
a set
of
adjacent
poly-
hedral
n-cells.
A
full
presentation
of
these methods
is
outside
the
scope
of
this book, where
we
have opted
to
describe
briefly
some
of the
most impor-
tant methods particularly
well
adapted
to the
modeling
of
natural objects.
For
more information
on
tesselation algorithms,
the
reader
is, for
example,
referred
to
[108, 169,
31,
88].
3.1
Introduction
All
through
the
chapters
of
this book
it is
assumed, whether implicitly
or
explicitly,
that
any
n-manifold
object
A to be
modeled
is
decomposed into
a
cellular
partition. Such
a
decomposition
is
used
for
building
a
discrete model
of
the
object
A
based
on an
n-dimensional graph
£(fi,
N)
denned
as
follows:
•
Q
=
{cti,a2,...}
is the set of all the
vertices
of all the
n-cells
used
in the
cellular
decomposition
of A.
•
TV
(a)
represents
the
subset
of fi
called
"neighborhood"
of a and
corresponding
to
vertices
directly
linked
to a by an
edge
of an
n-cell
of the
object
A.
• (a,
/3)
is an
edge
of
£(fi,
TV)
if, and
only
if,
f3
e
N(a).
Building
such cellular partitions
is
called "tessellation"
and
constitutes
a
very
active
field of
computational geometry.
An
exhaustive presentation
of
these
methods
is
beyond
the
scope
of
this
work,
in
itself necessitating several books.
For
this reason,
we
prefer
to
refer
to the
abundant literature devoted
to
this
topic.
For
example, among
the
most recent books
in
this
field, we can
mention
[31,
88,
169].
The
reader
is
also
referred
to
some works more
specifically
dedicated
to
geoscience problems
[51, 155, 217,
218].
97
