Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

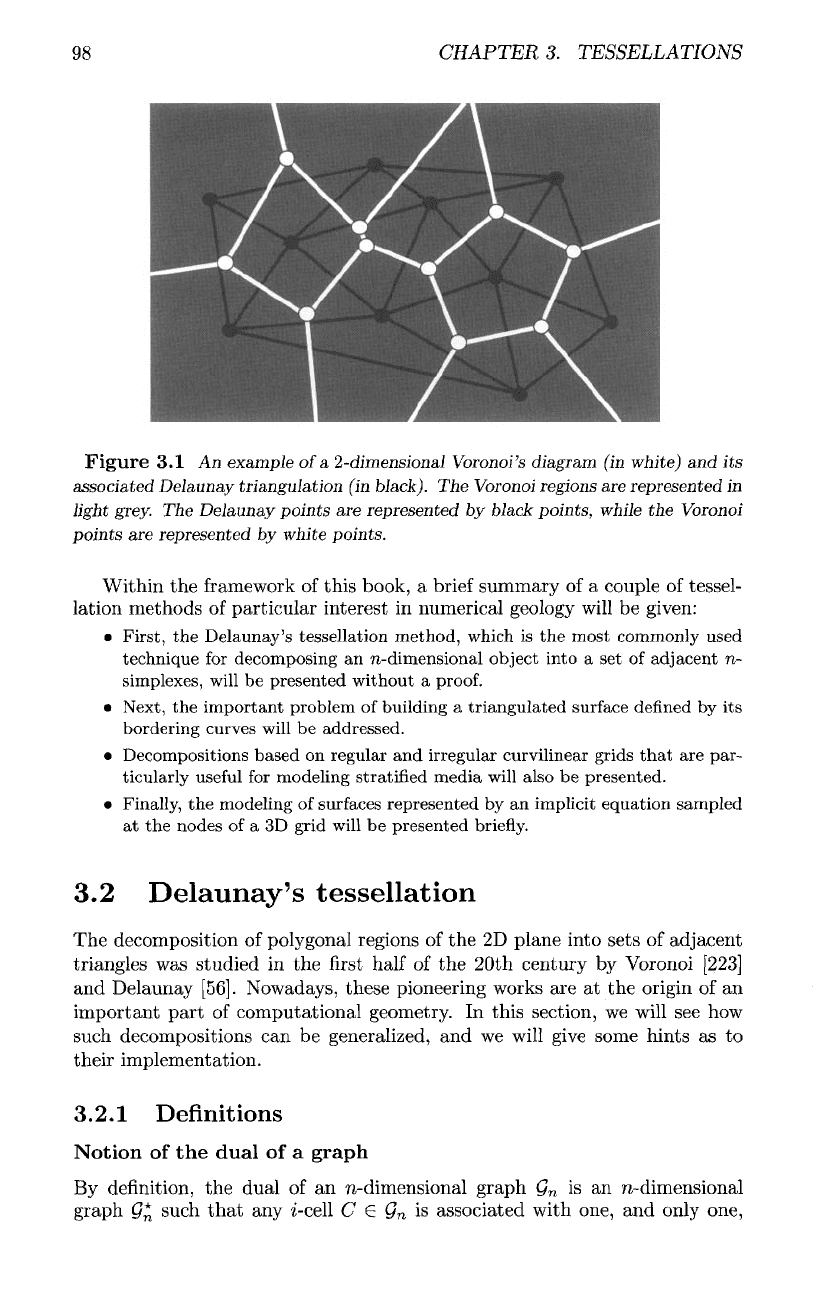
Figure
3.1 An
example
of
a
2-dimensional
Voronoi's
diagram
(in
white)
and its
associated
Delaunay triangulation
(in
black).
The
Voronoi
regions
are
represented
in
light grey.
The
Delaunay
points
are
represented
by
black
points,
while
the
Voronoi
points
are
represented
by
white
points.
Within
the
framework
of
this
book,
a
brief
summary
of a
couple
of
tessel-
lation
methods
of
particular
interest
in
numerical
geology
will
be
given:
•
First,
the
Delaunay's
tessellation
method, which
is the
most
commonly used
technique
for
decomposing
an
n-dimensional object into
a set of
adjacent
n-
simplexes,
will
be
presented without
a
proof.
•
Next,
the
important
problem
of
building
a
triangulated
surface
denned
by its
bordering curves will
be
addressed.
•
Decompositions based
on
regular
and
irregular curvilinear grids
that
are
par-
ticularly
useful
for
modeling stratified media will also
be
presented.
•
Finally,
the
modeling
of
surfaces
represented
by an
implicit
equation
sampled
at the
nodes
of a 3D
grid
will
be
presented
briefly.
3.2
Delaunay's tessellation
The
decomposition
of
polygonal
regions
of the 2D
plane
into
sets
of
adjacent
triangles
was
studied
in the first
half
of the
20th
century
by
Voronoi
[223]
and
Delaunay
[56].
Nowadays,
these
pioneering
works
are at the
origin
of an
important
part
of
computational
geometry.
In
this
section,
we
will
see how
such
decompositions
can be
generalized,
and we
will
give
some
hints
as to
their
implementation.
3.2.1
Definitions
Notion
of the
dual
of a
graph
By
definition,
the
dual
of an
n-dimensional
graph
Q
n
is an
n-dimensional
graph
£/*
such
that
any
^-cell
C E
Q
n
is
associated
with
one,
and
only
one,
CHAPTER 3. TESSELLATIONS
98

3.2.
DELAUNAY'S
TESSELLATION
It can be
observed
that
this
definition
is
symmetrical
and
this means
that
the
dual
of the
dual
(Q^Y
*
s
identical
to
Q
n
:
For
example,
figure
(3.1) shows,
in
bold,
a
2-dimensional
graph
£
2
with
its
dual
C/2
represented
in
white.
It can be
observed
that
•
each
2-cell
(region)
r
£
£2
is
associated
with
a
0-cell
(vertex)
v*
6
Q^,
•
each
1-cell
(edge)
e €
Qi
is
associated
with
a
1-cell
(edge)
e*
(E
Q^
an
d
•
each 0-cell (vertex)
v
£
$-2
is
associated
with
a
2-cell (region)
r* G
Q^.
It is
easy
to
imagine that,
in the
case
of a
3-dimensional
graph
£/
3
,
the
rela-
tionships
with
the
dual
Q\
can be
extended
as follows:
•
each
3-cell
(region)
r €
Qs
is
associated
with
a
0-cell (vertex)
v* e
£3,
•
each 2-cell
(face)
/ e
£3
is
associated with
a
1-cell (edge)
e* e
£3,
•
each 1-cell (edge)
e 6
(?3
is
associated with
a
2-cell
(face)
/* e
£3,
and
•
each 0-cell (vertex)
v
€
^3
is
associated with
a
3-cell (region)
r*
G
£3.
Notion
of
Voronoi's
diagram
and
Delaunay's
tessellation
Let
P =
{p
1
,...,p
m
}
be a set of
m
distinct
points
in the
n-dimensional
Euclidean
space
M
n
.
By
definition:
• We
note
as
V(p
i
)
and
call
it the
Voronoi region
of
p^
6 P, the
n-cell
of
IR
n
consisting
of all the
points
x
that
are
closest
to
p
i
than
any
other
point
of P:
As
shown
in the
shaded area
of figure
(3.1),
each
n-cell
V(p
i
)
is a
poly-
hedral cell containing
the
point
p^.
• We
note
as
VT>(P]
and
call
it the
Voronoi diagram
of P, the set of
points
of
M
n
that
do not
belong
to any
Voronoi region
V(p
i
):
As
shown
in figure
(3.1), Voronoi's diagram
consists
of an
n-dimensional
graph
(in
white) corresponding
to the
union
of the
boundaries
of the
Voronoi
regions.
• We
note
as
V(P)
and
call
it the
Voronoi tessellation
of P, the set of all
the
Voronoi regions
that
one can
build
on P.
99

100
Figure
3.2 An
example
of
a
2-dimensional
Delaunay
triangulation
(in
black):
the
circumcircle
(in
white)
of any
Delaunay
triangle
does
not
contain
any
other
vertex.
• We
note
as
<S(p
0
,
Pi,
• •
•,
p
n
)
and
call
it the
circumsphere
of a (n +
1)-
uplet
(pcuPi,
• •
-)P
n
)'
the
closed
ball
of
lR
n
whose boundary contains
the
points
(p
0
,Pi,
•
•-,pj.
• We
note
as
T(p
0
,p
1
,..
.,p
n
)
and
call
it the
Delaunay
triangle
1
of the
set
P, any
n-simplex
whose
vertices
(p
0
,p
1
,...,
p
n
)
belong
to P and
whose
circumsphere
<S(po,Pi>
• •
->P
n
)
does
not
contain
any
point
of P
in
its
interior.
• We
note
as
T>(P)
and
call
it
Delaunay's
tessellation
of P, the set of all
the
Delaunay triangles
that
one can
build
on
P.
3.2.2
Properties
Delaunay
theorem
The
Delaunay's tessellation
T>(P)
can be
identified with
the
dual V*(P)
of
the
Voronoi tessellation V(P):
This theorem
was
proven
in
1934
by
Delaunay
in the
particular case
n = 2
where
the
2-simplexes
are
actual
triangles.
For a
proof
of the
general case,
the
reader
is
referred,
for
example,
to
[169].
One can see in
figure
(3.1)
an
example
of
Delaunay's tessellation
(in
bold)
in
the
particular
case where
n = 2.
1
Note
that
a
Delaunay triangle
is a
real triangle only
in the
particular case where
n = 2.
In
the
case
where
n =
1,
a
Delaunay triangle
is
actually
a
segment,
and in the
case
where
n
=
3, a
Delaunay triangle
is a
tetrahedron.
CHAPTER 3. TESSELLATIONS

3.2.
DELAUNAY'S
TESSELLATION
Properties
of a
Voronoi's
diagram
V(P)
(VI)
Each Voronoi region
V(p
i
)
is
convex.
(V2)
A
Voronoi region
V(p
i
)
is an
unbounded
part
of
]R
n
if and
only
if
p^
is
on
the
convex hull
of P.
(V3)
The
Voronoi tessellation
V(P}
is a finite
cellular partition
of
lR
n
.
(V4)
If q is the
node
of the
Voronoi's diagram
VD(P]
located
at the
junction
of
(n + 1)
Voronoi regions
F(p
0
),
I^(PI),
•
•.,
V(p
n
),
then
q is the
center
of the
circumsphere
<S(p
0
,
p
l5
...,
p
n
)
and
this circumsphere does
not
contain
any
other point
of P.
Properties
of a
Delaunay's
tessellation
T>(P]
(Dl)
The
Delaunay's tessellation
T>(P]
can be
identified
with
the
dual
V*(P)
of
the
associated
Voronoi
tessellation
(Delaunay
theorem).
(D2)
The
boundary
of the
Delaunay's tessellation
'D(P)
is the
convex hull
of
the
point
set P.
(D3)
The
Delaunay's
tessellation
T)(P)
is a finite
cellular
partition
of the
interior
of the
convex hull
of the
point
set
P.
(D4)
In the
2-dimensional
case
(n = 2), the
Delaunay's tessellation
T>(P]
is
the
triangulation
of the
interior
of the
convex hull
of the
point
set P
that maximizes
the
smallest angle
of
each triangle.
(D5)
A
tessellation
made
up of
n-dimensional
simplexes whose vertices consist
of
a set of
points
P is a
Delaunay's tessellation
T>(P)
if, and
only
if, the
circumsphere
of any
n-simplex
T G
T>(P]
contains
no
vertex
of P
other
than
the
vertices
of T
(see
figure
(3.2)).
The
above property (D4) explains why,
in
2-dimensions, Delaunay triangula-
tions tend
to
generate "nice" triangles close
to
equilateral triangles. This
is
particularly important
for finite
element methods which
use
these
triangles
and
whose numerical stability depends
on the
shape
of
these elements.
Granularity
of a
Delaunay's
tessellation
T)(P}
For
n > 2, the
property (D4)
is no
longer applicable,
but one can
observe
that
the
Delaunay's tessellation still produces "nice" triangulations.
It is
only
in
1989
that
Raj
an
[178]
found
the
following
property, called
the
"property
of
granularity,"
which
in a way
generalizes
and
extends
the
above property (D4):
• let
A(P)
be a set of
adjacent
n-simplexes
generating
a
cellular
partition
of
the
interior
of the
convex
hull
of the
point
set P,
• let
s(T)
be the
smallest
sphere
containing
the
n-simplex
T, and
101

102
CHAPTER
3.
TESSELLATIONS
Figure
3.3
Mean
steps
of
the
insertion
of
a new
point
p in the
Bowyer-Watson
Delaunay's
tessellation algorithm
in the
2-dimensional
case:
(1) A new
point
p is
inserted
in a
triangle.
(2) The
triangle
t
containing
the new
point
is
retreived.
(3)
The set
Af(t\p)
of all the
triangles
to be
removed
is
determined.
(4) The
cavity
A/"(£|p)
is filled
with
new
Delaunay triangles.
• let
Grain(A(P))
be the
radius
of the
largest sphere
s(T)
associated with
the
simplexes
of
A(P):
Rajan's granularity property guarantees
that
the
Delaunay's tessellation
T>(P)
is
optimal
in the
following
sense:
3.2.3
An
incremental algorithm
Many
algorithms have been proposed
in the
literature
for
building Delau-
nay
tessellations.
In
this section
we
present
an
incremental algorithm inde-
pendently proposed
by
Bowyer
[33]
and
Watson [226]
that
has the
following
advantages:
•
This algorithm
is
independent
of the
dimension
n of the
simplexes being built.
• The
implementation
of
this algorithm
is
simple.
•
This algorithm
can be
used
for
editing
an
existing Delaunay's tessellation
by
inserting
new
points.

3.2.
DELAUNAY'S TESSELLATION
Bowyer-Watson
incremental algorithm
Let
us
assume
that
a
Delaunay's
tessellation
V(P]
is
already known
for a
given
point
set P and we
would like
to add a new
point
p to P and
build
a new
Delaunay's tessellation
T>(P(J{p}).
In
this case, Bowyer
and
Watson propose
using
the following
incremental algorithm whose principle
is
illustrated
in
figure (3.3):
//—
Bowyer-Watson
algorithm^!
•
Find
the
n-simplex
t
G
T)(P}
containing
p
•
Build
the
subset
A/"(i|p)
consisting
of all the
n-simplexes
of
T)(P]
whose
circumsphere
contains
p in its
interior
•
Build
the
subset
M*(t\p)
consisting
of the set of all the
n-simplexes
corresponding
to a new
partition
of
the
region
N(t\p)
by
n-simplexes
sharing
the
vertex
p
•
Build
D(PU{p})
=
T>(P)
-
N(t\p)
+
N*(t\p)
Two
comments must
be
made about this algorithm:
• If a
light spot
is put at
location
p,
then
one can
show
that
all the
vertices
of
cW(£|p)
are
"lit up."
As a
consequence,
jV*(£|p)
consists
of
all the
n-simplexes having
p as a
vertex whose opposite "face"
is a
(n
—
l)-simplexes
of
cW(t|p).
• The
determination
of the
n-simplex
t
containing
a
point
p can be
per-
formed
efficiently
thanks
to the
following
algorithm (see
figure
(3.3)
- top
right)
which takes advantage
of the
orientation
of the
"faces"
((n
—
1)-
simplexes)
of
each n-simplex
t £
*D(P}\
//—
Bowyer-Watson
algorithni#2
• t
<—
any
n-simplex
of
T>(P)
•
found
<—
false
while
(
found
! =
true
) {
for_all(
face
/ of t ) {
• let
pj
be the
vertex
of t
opposite
to /
if(
p and
p
f
are on two
sides
of / ) {
• t
<—
simplex
adjacent
to t and
sharing
/
with
t
•
found
«—
true
• go to
newJ,
}
else
{
•
found
<—
false
}//-
end:
if_else
} //-
end:
for_all
newJ,
}
//-
end: while
The
Bowyer-Watson
algorithm
#1
can
easily
be
turned into
an
algorithm
able
to
build
the
Delaunay's tessellation
T>(P)
of any
point
set P. For
this
purpose,
the
following
algorithm
can be
used:
103

104
Figur e
3.4
Constrained
2-dimensional
tessellation:
principle
of
the
"edge
swap"
algorithm.
//—
Bowyer-Watson
algorithm's
• Let To be an
initial
n-simplex
chosen
in
such
a way
that
it
contains
all the
points
of P
• Let
PQ
be the
point
set
consisting
of the (n + 1)
vertices
of
TO
• Let
X>(Po)
= To
for_all(p€P)
{
• Use the
Bowyer-Watson
algorithm
#1:
} //
end:
for_all
• Let
£>(Po;Tb)
be the
subset
of
£>(Po)
consisting
of all
the
n-simplexes
sharing
a
vertex
with
TO
•
Build
P(P)
=
£>(P
0
)
-
£>(Po;T
0
)
The
Delaunay
constrained
tessellation:
2-dimensional
case
Let
P be a
given
set of
points
in the 2D
plane
and let 8 be a set of
segments
such
that
the
vertices
of any
segment
e
E €
belong
to P; in
addition,
we
assume
that
the
segments
of £ do not
cross each other.
By
definition,
we
note
as
T>(P\£]
and
call
it
"Delaunay's
tessellation
of P
constrained
by
£,"
any
set of
adjacent triangles deduced
from
V(P)
in
such
a way
that
any
segment
e
G £ is the
edge
of at
least
one
triangle
of
T>(P\£).
Before
presenting
an
algorithm able
to
construct
T>(P\£)
from
T)(P),
let
us
define
the
"edge swap" operation
as
follows:
if two
adjacent triangles
T(p
0
,Pi,
P
2
)
and
T(PQ,
p
l5
p
2
)
share
a
common edge
(p
l5
p
2
),
then
this
edge
is
said
to be
"swapped"
if the two
initial triangles
are
replaced
by two new
triangles
T(p
l
,
P
0
,
Po,)
and
T(p
2
,
p
0
,
pj$,).
Using
this
"edge swap" operation,
Cherfils
and
Hermeline [44] have shown
that
the
following
very simple "edge swap algorithm," illustrated
in figure
CHAPTER 3. TESSELLATIONS

3.2.
Figure
3.5
Constrained
2-dimensional
Delaunay's tessellation
of
the
interior
of
a
close curve,
without
internal
points
(left)
and
with
internal
points
(right).
(3.4),
converges
and
iteratively transforms
a
triangulation
T>(P]
into
a
con-
strained
triangulation
T>(P\£]
respecting
the
segments
of
£:
If—
Edge
swap
algorithm
(2D
case)
•
V(P\£]
<—
T>(P)
• ok
<—
false
while
( ok !
=
true
) {
• ok
<—
true
for_all(
segment
e E £ ) {
let £* be the
current
set of the
edges
of
the
triangles
of
T>(P\£]
that
intersect
e
if(£V0)
{
• ok
*—
false
for_all(
e* € £
*
) {
•
swap
the
edge
e* and
update
T>(P\£)
}
//-
end:
for_all
} //-
end:
if
} //-
end:
for_all
} //-
end:
while
The
planar
closed
curve
Delaunay's
tessellation
As
a
consequence
of the
edge swap algorithm presented above,
if the
segments
of
£
constitute
a
planar closed curve
and if P is a
given point set, then,
as
shown
in figure
(3.5),
it is
easy
to
build
a
triangulation
filling the
interior
of
this curve:
for
that
purpose,
we
have only
to
build
a
constrained tessellation
T>(P\£)
and
then
to
remove
all the
triangles
that
have
a
center
of
gravity
outside
the
closed curve generated
by £. As
suggested
by figure
(3.5),
one can
easily
imagine
the
following
algorithm
for
inserting dynamically points
in P
at
select
locations
to
improve
the
quality
of the
tessellation:
DELAUNAY'S TESSELLATION
105

106
CHAPTER
3.
TESSELLATIONS
Figure
3.6
Switching
a
face
of
tetrahedra
f
with
an
edge
e
replaces
the two
tetrahedra
sharing
the
face
f by
three
tetrahedra
sharing
the
edge
e.
//—
Planar closed curve Delaunay's tessellation
• let £ = set of
edges
of a
closed
curve
• let P = set of
vertices
of £
•
compute
T>(P)
while(
'D(P)
is not
optimal
) {
•
look
for the
"ugliest"
triangle
T
u
of
D(P)
•
compute
the
barycenter
p of
T
u
• use the
Bowyer-Watson
algorithm
for
inserting
p in P and
£>(P)
}
• use the
edge
swap
algorithm
for
computing
£>(P|£)
•
remove
from
£>(P|£)
the
triangles
whose
barycenter
is
outside
the
closed
curve
associated
with
8.
This
simple algorithm
can be
adapted
in
many
different
ways depending
on
the
properties
one
wishes
to
obtain
for the
resulting tessellation
(e.g.,
see
[51]).
The
Delaunay
constrained
tessellation:
3-dimensional
case
Let
P be a
given
set of
points
in the 3D
space,
and let T be a set of
triangles
such
that
the
vertices
of any
triangle
t 6 T
belong
to P; in
addition,
it is
assumed
that
the
triangles
of T do not
cross each other.
By
definition,
we
note
as
Z>(P|T)
and
call
it
"Delaunay's
tessellation
of
P
constrained
by T"
any set of
adjacent tetrahedra deduced
from
T>(P)
in
such
a way
that
any
triangle
t G T is the
face
of at
least
one
tetrahedron
of
£>(P|
T).
It is
possible
to
extend
the
edge swap algorithm
to the
3-dimensional case,
but
this
is
considerably more complex than
in 2
dimensions.
As
suggested
in
figure
(3.6),
one of the
origins
of
this increased complexity
is
that
a 3D
edge
of
ta
etrahedron must
now be
swapped with
a 3D
face
of a
tetrahedron,
that
is
to
say,
a
triangle. This type
of
algorithm will
not be
presented;
refer
to
[88]
for
an
exhaustive presentation
of
such
an
approach.

3.2.
Figure
3.7
Constrained
^-dimensional
Delaunay's
tessellation
of the
union
of
a
series
of
adjacent
complex
geological
regions.
The
edges
of the
tetrahedra
are
constrained
not to
cross
the
horizons
and
fault
surfaces.
A
simpler method consists
in
allowing
the
insertion
in P of new
points
located
on the
triangles
of
T.
In
practice,
these
additional points, called
"Steiner's
points"
are
chosen iteratively
on the
current triangles
of T
inter-
sected
by
some edges
of
£>(P|T).
The
insertion
of
these
new
points changes
the
tessellation locally
and
tends
to
remove
the
undesirable intersections. Fig-
ure
(3.7) gives
an
example
of
3-dimensional
tessellation obtained with this
approach:
as
shown
in
this
figure, the
interior
of
complex geological regions
bounded
by
closed surfaces
can be
tessellated
while
preventing
the
edges
of
the
tetrahedra
from
cutting these
surfaces.
3.2.4
Sculpting
a
point
set
There
are
some applications where
an
unknown solid
is
defined
by an
unstruc-
tured
set of
points corresponding
to a
sampling
of
this solid
in 3D
space.
In
such
a
case,
one can
think
of
using
the 3D
Delaunay's tessellation algorithm
for
building
a
discrete model
of
this
solid
as
follows:
1.
Use the
unconstrained
3D
Delaunay's
tessellation
algorithm
to
build
the
small-
est
convex
solid
containing
the
given
set of
points.
2.
Remove
simplexes
from
this
solid
to
build
a
non-convex
"shape" approximat-
ing,
as far as
possible,
the
unknown
solid.
Depending
on the
strategy
used
for
removing simplexes
from
the
initial convex
solid,
one can
distinguish
the
following
methods:
DELAUNAY'S TESSELLATION
107
