Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


78
CHAPTER
2.
CELLULAR PARTITIONS
These preconditions
(1) and (2)
specify
that
F
0
and
FI
must
be
free
boundaries
of
CQ
and
Ci,
while
precondition
(3)
allows
us to
define
an
isomorphism
27
between
the
subcells
of
FQ
and
F\.
If
these preconditions
are
honored, then
the
sewing operation
is
per-
formed
as
follows:
1.
For all
pairs
of
Darts
(d'
Q
,d'i)
incident
to
(Fo,Fi)
do:
This operation generates
a
common
face
F
resulting
from
the
merging
of
FQ
and
F\.
2.
For all i
G
[0,n]
and for
each
i-cell
C
incident
to F do:
—
if C has
several embeddings, then discard
all but one and
dispatch
the
remaining
one to
each Dart incident
to the new
common
face
F.
unsew_cell(n,
gm,
do)
unsews
the (n
—
l)-cell
F
incident
to a
given Dart
do
in the
n-GMap
gm.
This
operation consists
in
"freeing"
all the
Darts
incident
to F and is
performed
as
follows
without
any
precondition:
1.
Initialize:
2.
For all
Darts
d
incident
to F do:
This
operation generates
a new (n
—
l)-cell
F'
incident
to
di
3. For all i € [0,
n]
and for
each
i-cell
C
incident
to F or
F'
do:
—
if C
does
not
have
an
embedding, then create
one and
dispatch
it
to the
other
C
Darts;
the
value
for
this
new
embedding
is
copied
from
the
previous shared embedding.
•
merge_gmap(n,gm,
added-gm)
adds
all the
Darts
and
abstract cells
of
the
n-GMap
added-gm
to the
n-GMap
gm.
This operation
is
only
possible
if the two
GMaps have
the
same dimension
n and are
embedded
in
the
same space
JR
m
.
27
See
definition
on
page
44.
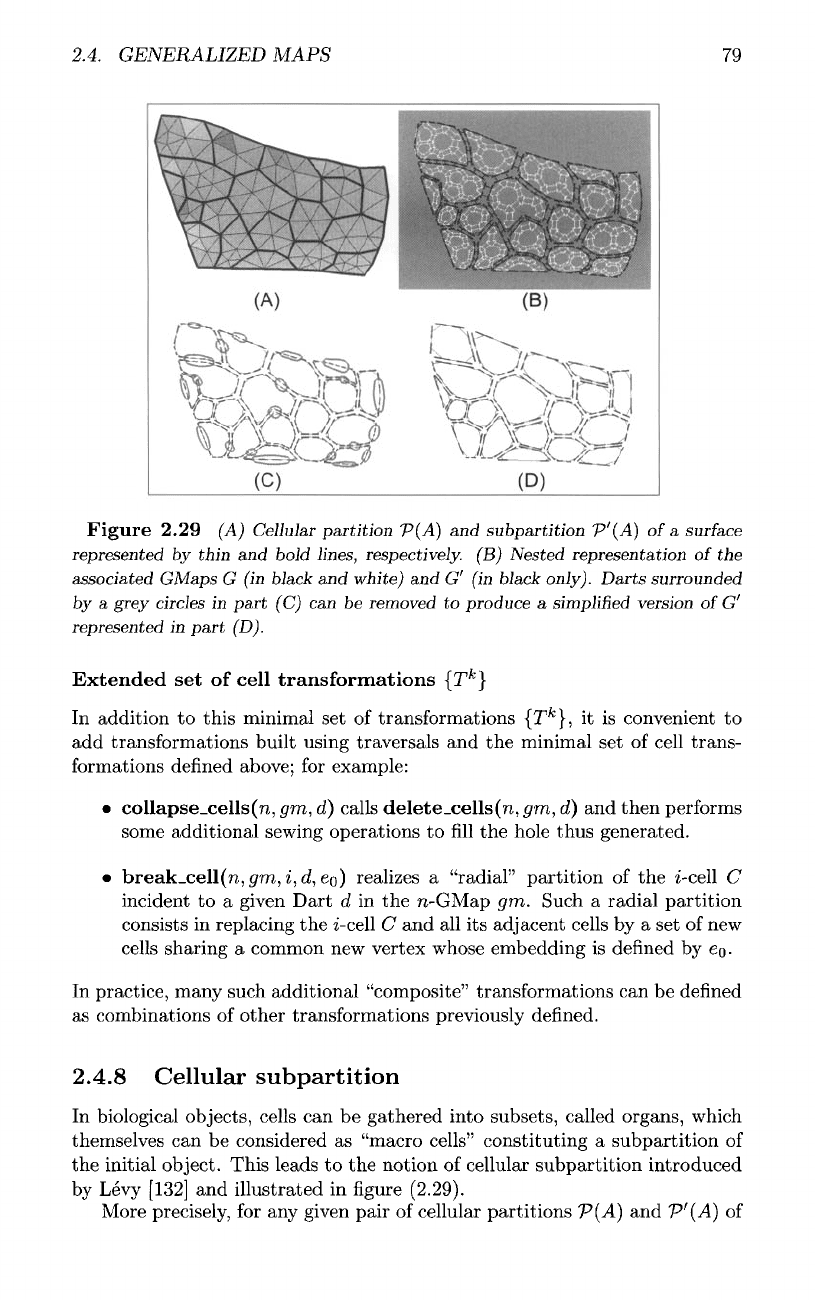
2.4. GENERALIZED MAPS
79
Figure
2.29
(A)
Cellular
partition
P(A)
and
subpartition
P'(A)
of
a
surface
represented
by
thin
and
bold
lines,
respectively.
(B)
Nested
representation
of the
associated
GMaps
G (in
black
and
white)
and G' (in
black
only).
Darts
surrounded
by a
grey
circles
in
part
(C) can be
removed
to
produce
a
simplified
version
of
G'
represented
in
part (D).
Extended
set of
cell
transformations
{T
k
}
In
addition
to
this minimal
set of
transformations
{T
fc
},
it is
convenient
to
add
transformations built using traversals
and the
minimal
set of
cell trans-
formations
defined
above;
for
example:
•
collapse_cells(n,
gm,
d)
calls
delete_cells(n,
gm,
d) and
then performs
some additional sewing operations
to fill the
hole thus generated.
•
break_cell(n,gra,
i,d,
eg)
realizes
a
"radial" partition
of the
i-cell
C
incident
to a
given Dart
d in the
n-GMap
gm.
Such
a
radial partition
consists
in
replacing
the
2-cell
C and all its
adjacent cells
by a set of new
cells sharing
a
common
new
vertex whose embedding
is
defined
by
CQ.
In
practice, many such additional "composite" transformations
can be
defined
as
combinations
of
other transformations previously
defined.
2.4.8
Cellular subpartition
In
biological objects, cells
can be
gathered into subsets, called organs, which
themselves
can be
considered
as
"macro cells" constituting
a
subpartition
of
the
initial
object.
This
leads
to the
notion
of
cellular
subpartition
introduced
by
Levy [132]
and
illustrated
in figure
(2.29).
More precisely,
for any
given pair
of
cellular partitions
P(A)
and P' (A) of

80
CHAPTER
2.
CELLULAR PARTITIONS
a
manifold object
A,
P'(A)
is a
cellular subpartition
of
P(A)
if:
For
example,
in figure
(2.29)-A,
thin
lines
represent
a
cellular
partition
P(A)
of
a
surface
A
while bold lines represent
a
cellular subpartition
P'(A]
of
P(A).
If
the
cellular partition
P(A)
is
represented
by a
GMap
G =
Cj(D,ao,..
.,a
n
),
then building
a
cellular subpartition
P'(A)
of
P(A)
is
equivalent
to
splitting
D
into
a
series
of
subsets
{.Di,...,
D
w
},
with each
of
them corresponding
to
a
"macro"
n-cell
28
of
P'(A)
and
honoring
the
following
constraints:
It is
then possible
to
represent
P'(A)
by a
GMap
G' =
G(D',
a'
0
,...,
a'
n
)
fully
deduced
from
G and
such
that
The
basic idea
is to
consider
the
GMap
of the
boundaries associated with
the
subsets
{£>i,...,
D
N
}
and to
link
the
latter
by a
function
o!
i
denned
as
follows:
It is
verifiable
(see
[132])
that
the
combinatorial structure
G'
so
defined
is
actually
a
GMap.
Figure
(2.29)-B
shows
the
GMap
G
corresponding
to the
cellular partition
represented
by
thin
lines
in figure
(2.29)-A,
while
figure
(2.29)-C
shows
the
GMap
G'
associated with
the
cellular subpartition represented
by
bold lines
in figure
(2.29)-A.
Simplifying
a
cellular
subpartition
It is
always possible
to
simplify
the
boundaries
of the
macro
n-cells
of a
cellular
subpartition
by
replacing
a
series
of
Darts
by one or two
"macro Darts."
For
example,
in figure
(2.29)-C,
each series
of
Darts surrounded
by a
grey circles
can be
replaced
by one or two
macro Darts represented
in figure
(2.29)-D.
28
For
example,
in
figure (2.29), such
a
"macro"
n-cell
corresponds
to a set of
triangles
bounded
by a
bold line.

2.5. IMPLEMENTING GMAP-BASED MODELS
81
Figure
2.30
(A)
Horizon
and
fault
surfaces
corresponding
to the
boundaries
between
geological
layers:
the
union
of all
these
(2-manifold)
surfaces
generates
a
non-manifold
object
that
cannot
be
represented
by a
GMap.
(B) The
volume
denned
as a
partition
of the 3D
space
generated
by the
horizon
and
fault
surfaces
(2-Dividing-Walls)
is a
3-manifold
object
that
can be
represented
by a
3-GMap.
2.5
Implementing GMap-based models
So
far,
the
notion
of
GMap
has
been considered
as a
theoretical framework
allowing
the
topology
of
cellular partitions
of
manifold objects
to be
described.
It
must
be
noted, however,
that
Darts
and
involutions used
in
GMaps
are
very
basic notions
that
are far
from
geological concepts such
as
horizons
and
layers.
For
this reason,
if we
want
to
implement
a
topological model based
on
GMaps,
we
need
to
consider
two
levels
of
concepts:
• a
"basic"
level
(see
section
(2.5.2))
corresponding
to the
implementation
of
the
notions
of
Darts,
involutions
and
GMap,
and
• an
"advanced"
level
(see section
(2.5.3))
corresponding
more
directly
to
geo-
logical
objects.
From
a
practical
point
of
view,
there
are
many
different
possible
implementa-
tions
of
these
two
levels
of
concepts;
as an
example,
in
this section
the
outlines
of
the
implementation used
in the
gOcad software
are
presented.
2.5.1
In
practice,
the
modeling
of an
object
A* can be
considered
from
two
points
of
view:
•
either
we try to
model
the
object
A*
itself
and
this
leads
to
"Boolean"
or
"Brep"
approaches
[183],
• or we
consider
the
elements
of A* as
contributing
to the
partition
P(A)
of a
manifold
object
A
containing
A*
which
leads
to the
notion
of
cellular
model.
Within
the
framework
of
section
(2.5),
we
will
see how
GMaps
can be
actu-
ally used
for
building cellular models
in a
hierarchical
way.
In the
proposed
approach,
as
suggested
in figures
(2.17),
and
(2.30),
let it be
assumed
that
Introduction

82
CHAPTER
2.
CELLULAR PARTITIONS
• the
manifold
object
A to be
partitioned, called
the
"universe,"
is
identical
to the
whole space
lR
n+l
:
• the
object
A* to be
modeled
is
fully
contained
in the
universe
A and
consists
of
a
series
of
elements
{Wi,...,
WN}
called "dividing walls,"
that
correspond
o
o
to
n-manifolds
objects whose interiors
{WI,---,WN}
do not
intersect each
other:
•
isolated objects with
a
topological dimension
lower
than
n do not
contribute
to
the
partition
"P(A),
but can be
added
to the
model
as
"decoration"
elements.
It
should
be
noted
that
decoration
elements
could
also
be
included
in the
topological
model.
For
this
purpose,
instead
of
considering
a
model
as a
GMap,
it
would
be
necessary
to
consider
a
model
as
composed
of a
"chain"
of
GMaps
{G^,
G^
2
,...}.
In
such
a
model,
each
G
3
n
.
could
then
be
considered
as an
"extended"
nj-GMap
[73]
with
the
following form
where
a is a set of
permutations
allowing
"navigation"
from
a
Dart
in the
Tij-GMap
G
3
n
.
to
Darts
of an
adjacent
GMap.
As
already
mentioned,
in the
realm
of
geomodeling
such
an
extension
is
not
really
necessary
and
will
not be
presented
in
this
book.
A
geological
example
of a 3D
cellular
model
As
suggested
in
figures
(2.1),
(2.30),
and
(2.34),
if
A*
consists
of
geological
horizons
and
fault surfaces [155, 69],
then:
• the
universe
A is the
whole
3D
space,
or a
part
of the
3D
space, bounded
by a
bounding box, which constitutes
the
(n
+ 1
=
3)-dimensional object
to be
split
by the
elements
of
A*,
•
dividing walls correspond
to
horizons
and
faults (dim=
n =
2),
and
•
decoration elements
may
correspond,
for
example,
to
well-paths
(dim=
n
—
1 = 1) or
scattered
data
points (dim=
n
—
2 =
0).
A
geological
example
of a 2D
cellular
model
As
suggested
in
figures (2.2),
and
(2.17),
if A*
consists
of a set of
curves
corresponding
to the
intersections
of the
horizons
and
faults
with
a
finite
or
infinite
open
surface
29
X,
called
"cross
section"
[155],
then:
• the
universe
A is
identical
to X and
constitutes
the
(n
+ 1 =
2)-dimensional object
to be
split
by the
elements
of
A*,
•
dividing walls correspond
to
curves
(dim=
n = 1)
induced
by the
intersections
of
horizons
and
fault
surfaces
with
the
cross section
X,
and
29
Note
that
X may be a
plane
or a
curved surface
that
does
not
self-intersect.

2.5.
IMPLEMENTING GMAP-BASED MODELS
•
decoration
elements
may
correspond,
for
example,
to
scattered data
points
(dim=n-
1 = 0).
Notion
of
virtual
Darts
When constructing
a
brass
statue,
it is
always
necessary
to
build small
tubes
connecting
the
exterior
to the
interior
of the
mold into which
the
melt metal
is
poured. Once
the
statue
is
completed,
the
metallic
parts
(barbs) generated
by
these small tubes
are
removed
to
preserve
the
aesthetic aspect
of the
statue.
Similarly,
as
shown
in
figure
(2.17),
GMaps
may
need
"unaesthetic
small
tubes"
in the
following
two
cases:
• in the
connections
between
the
object
A* to be
modeled
and the
boundary
of
the
universe
A, and
• in the
connections
between
a
dividing
wall
30
not
connected
to
other
dividing
walls.
The
cells corresponding
to
these
connections and, more generally,
any
cell
considered
of no
use,
can be
declared "virtual."
The
Darts incident
to
these
virtual cells
are
called "virtual Darts"
and do not
need
to
have
an
embed-
ding.
In
practice,
the
virtual cells
and
their associated virtual
Darts
are not
displayed
in
graphical applications.
2.5.2
Basic level: GMaps
From
a
computer science point
of
view,
the
notion
of
GMap
can be
imple-
mented
in
many
different
ways
and the
complete description
of
such imple-
mentations
is far
beyond
the
scope
of
this book.
In
this section,
we
merely
give
the
outlines
of a
possible implementation based
on the C++
language:
31
Notion
of
Store
For the
sake
of
clarity,
in the
rest
of
this section,
we
will
call "Store"
any
C++
class with
the
following
prototype:
class
StuffStore
{
Stuff
create_stuff();
void
destroy_stuff(
Stuff
s
);
Stuff
get_stuff(
Gid gid
);
Gid
get_gid( Stuff
s
);
private:
//—
info related
to a
database
// for
Stuff
objects
}
30
In
geology,
this
is the
case,
for
example,
when
a
lens
(internal
region)
is
fully
contained
in
a
layer
(external
region).
31
In
practice,
for
efficiency
reasons,
a
real
implementation
of
Darts
and
GMaps should
be
quite
different
and
much
more
complex,
but
conceptually
close
to the
simplified
presentation
proposed
in
this section.
83

84
CHAPTER
2.
CELLULAR PARTITIONS
Such
a
class
is
assumed
to
implement
an
interface with
a
database
for
objects
belonging
to the
Stuff
class,
and the
member
functions
offer
the following
services:
•
create-stuff(
) is
assumed
to
—
create
a new
Stuff
object,
—
if
needed, store
the new
Stuff
object
in the
StuffStore,
and
—
return
the new
Stuff
object.
•
destroy-Stuff(s)
is
assumed
to
remove
the
Stuff
object
s
from
the
Stuff-
Store
and
then,
if
need
be,
delete
it.
•
get-stuff(gid)
is
assumed
to
return
the
Stuff
object, contained
in the
database
and
associated
with
the key gid
belonging
to the Gid
abstract
class (Gid
is an
acronym
for
Generalized-identifier).
•
get-gid(s)
is
assumed
to
return
the Gid of the
object
s
contained
in the
database.
A
naive
implementation
of
GMaps
Prom
a
conceptual point
of
view,
the
Darts
of an
n-GMap
could
be
represented
as the
following
recursive
data
structure:
class
Dart
{
private:
//
n
= dim of the
GMap
Dart
*alpha_[n+1];
Gid
embedding_[n+l];
Boolean
mark_[32];
}
Assuming
that
n < 30 is the
dimension
32
of the
associated n-GMap,
the
private
fields of
such
a
data
structure hold
the
following
information where
the
index
i is
assumed
to
belong
to
[0,n]:
•
alpha
..[i]
is the
address
of the
Dart linked
to the
current Dart
by an
c^
involution.
•
embedding-[i]
is the Gid
corresponding
to a key
enabling retrieval
of
the
i-embedding
of the
current Dart
in the
database assumed
to be
implemented
as an
instance
of the
EmbeddingStore class.
• raar/c_[32] is an
array
of 32
bits used
to
mark
the
Darts:
—
the (n + 1) first
entries
marfc_[0]
to
mark-[n]
are
reserved
for
storing
flags
in
such
a way
that
mark^i]
—
true
means
that
the
current
Dart
is
marked
as an
"i-cell-key"
used
by the
CellManager
(see
explanation
below),
32
Note
that
this
is
simply
a
practical programming assumption, allowing
the
array
_marfc[32]
to be
implemented
as a
32-bit word.

2.5.
IMPLEMENTING GMAP-BASED MODELS
85
—
the
entry
mark-[n
+
I]
is
equal
to
true
if the
current Dart
is
virtual,
and
—
the (32
—
(n
+
2))
remaining
entries
of
mark-[-]
can be
used dynamically
for
storing temporary
flags in
algorithms using
Darts
(z-orbit
traversal,
i-cell
iterator,
...).
Theoretically,
to
ensure
the
consistency
of the
embeddings
(see section
(2.4.2)),
all the
Darts
of an
z-orbit
should have
the
same
Gid
stored
in
their respective
embedding_[i]
private
buffers.
To
guarantee
that
such
a
property
is
always
true, each
instance
of the
GMap
class
contains
an
instance
of the
CellMan-
ager class
that
uses
the
following
strategy when applied
to a
given Dart
of the
GMap:
• If
there
is
only
one
i-cell-key
Dart
in the
i-orbit
of the
current Dart
managed
by the
CellManager,
then
do
nothing.
• If
there
are
more than
one
z-cell-key
Darts
in the
z-orbit
of the
current
Dart managed
by the
CellManager, then choose
one
i-cell-key
Dart
in
the
z-orbit
and:
—
set the flag
mark-[i]
of all the
others
Darts
of the
i-orbit
to
false,
and
—
find the Gid of the
embedding
of the
z-cell-key
Dart
of the
i-orbit
and
assign
its
value
to the field
embedding-[i]
of all the
Darts
of the
z-orbit.
As
a
consequence,
from
a
conceptual point
of
view,
the
implementation
of
an
n-GMap
associated with such
a
Dart
data
structure should look
like
the
following:
class
GMap
{ //
n
= dim of the
GMap
public:
GMap(
int n
);
private:
int n_; //
n_=n
Set<Dart*>
darts_;
CellManager
cm_;
BoolMarkManager
bmm_;
EmbeddingStore
es_;
}
In
this
data
structure,
the
BoolMarkManager class
is
assumed
to be in
charge
of
the
management
of the (32
—
(n +
2))
last
bits
of the flags
stored
in the
mark[-]
array
of the
Darts.
In
particular,
the
BoolMarkManager provides
a
mechanism
preventing
the
situation where
two
different
algorithms might
try
to use the
same
bit at the
same time.
2.5.3
Advanced
level:
Notion
of
Model
In
geomodeling applications, users want
to
build easily partitions
of the 3D
space corresponding,
for
example,
to
geological layers
and
fault
blocks.
As

86
CHAPTER
2.
CELLULAR PARTITIONS
figures
(2.30),
and
(2.32)
show,
during
the
modeling process,
2-manifold
sur-
faces
corresponding
to
horizons
and
faults
are
built
and
then
assembled: such
an
assembling operation generates non-manifold configurations similar
to the
binding
of the
pages
of a
book
that
cannot
be
directly represented
by a
GMap.
As
suggested
in
figure
(2.30),
rather than trying
to
model
the
non-manifold
topological
relationships between
a set of
surfaces
{Wi,...,
WN}
directly,
it is
more
relevant
to
consider
a
cellular partition
P(1R
3
}
of the 3D
space honoring
the
following
constraint:
33
Any
cellular partition
P(1R
) so
generated
can be
represented
by a
3-GMap.
Similarly
and as
illustrated
in figure
(2.17),
a set of
1-manifold
curves
in
the 2D
space
can be
assembled
in a
non-manifold
way to
build
a
partition
of
this
2D
space.
More
generally,
the
technique
of
partitioning
the
IR
n+l
space
by a
series
of
n-manifold objects whose union
is
non-manifold
is the
solution proposed
by
Levy [132]
and
presented
in
this section
for
implementing advanced level
concepts
such
as the
notions
of
Model, Region, Frame
and
Edge.
In
practice,
these concepts should
be
translated
in
terms
of
data
structures
not
described
in
this book.
Notions
of
Dividing-Wall,
Frame,
and
Edge
By
definition,
any
orientable
n-manifold object
W
embedded
in the
M
n+l
space
is
called
an
n-Dividing-Wall
of
M
n+l
or,
more simply,
a
Dividing-
Wall.
Moreover,
for any
cellular partition
P(lR
n+l
)
honoring
the
following
constraint,
34
we
will
say
that
• the
(n+l)-GMap
F(W)
=
Q(D~\JD^,o^,..
.,a£+i)
associated
with
P(M
n+1
)
is
a
Frame
of
W,
and
• the (n -
l)-cells
of
F(W]
are the
Edges
of
F(W).
Note
that,
due to the
orientability
of W and as
explained
on
page
71, the set
of
Darts
belonging
to the
GMap
F(W)
can
always
be
split
into twin
sets
Dp
and
D~p
such
that
This allows
the
notions
of
positive side
F
+
(W)
and
negative side
F~(W)
of
the
Frame
F(W)
to be
defined
as the
following
twin isomorphic
(n
—
1)-
33
Recall
that
Pi(A)
is the set of
i-cells
of
P(A).
Note
that
we are
interested
only
in
vertices
contributing
to the
description
of the
boundary
of
W.

2.5. IMPLEMENTING GMAP-BASED MODELS
87
Figure
2.31
In a
Model,
each
n-Dividing-Wall
W
generates
a
cellular
partition
P(]R
n+l
)
of the
embedding
space
and is
associated
with
a
"Frame"
F =
F(W]
consisting
of
an (n +
l)-GMap
of
this partition.
Such
a
Frame
F =
F(W)
delegates
the
responsibility
for its
embedding
to a
Lattice
L(W)
whose
cellular
partition
is in
turn
associated
with
an
n-GMap.
According
to
equations
(2.41)-2,
it is
clear
that
both
F
+
(W)
and F (W) can
be
identified with GMaps
of the
boundary
of
W.
An
illustration
of the
notions
of
Dividing-Wall,
Frame,
and
Edge
can be
found
in figure
(2.31). Figure
(2.36)
shows
a
wireframe
representation
of the
Frames associated with
the
Dividing-Walls
presented
in figure
(2.34).
Delegation
of
embedding:
Notion
of
Lattice
Let
W be an
n-Dividing-Wall.
For any
cellular partition P(W)
of W, the
associated n-GMap
is
called
a
Lattice
of W.
Let
us now
consider
the
(n—
l)-GMap
dL(W)
of the
boundary
35
of
L(W)
and
let
dL'(W)
be the
(n—l)-GMap
corresponding
to a
given cellular
subpartition
36
of
this boundary:
35
See
definition
on
page
60.
36
See
definition
on
page
79. It
should
be
noted
that,
if
need
be,
this
subpartition
may be
identical
to the
full
initial
partition
dL(W).
GMaps:
