Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


108
cn-shapes
To
each simplex
a
consisting
of an
edge,
a
triangle
or a
tetrahedron
of the
initial
3D
Delaunay
tetrahedralization,
we can
associate
a
coefficient
a(<r)
such
that
where
S(a]
is the
circumsphere (see page 100)
of a.
Edelsbrunner
and
Mucke
[71] propose removing
from
the
initial
3D
Delau-
nay
tetrahedralization
all the
simplexes whose
coefficient
a
(a) is
greater
than
a
positive parameter
a
given interactively
by the
user. They propose calling
the
subset
of
simplexes
so
generated
a-shape.
We can
make
the
following
observations (see
[51])
concerning
the
results
of
this method:
•
From
an
aesthetic
point
of
view,
the
shapes
so
generated
are
acceptable
and it
is
generally
possible
to set the
parameter
a
interactively
to
obtain
the
desired
shape.
•
Prom
a
practical
point
of
view,
a-shapes
are
only
"shapes"
composed
of
incon-
sistent
sets
of
edges,
triangles,
and
tetrahedra
that
cannot
be
used
for
discrete
modeling
purposes.
/3-shapes
To
each
tetrahedra
t
belonging
to the
initial
3D
Delaunay tetrahedralization,
we
can
associate
a
coefficient
b(t)
such
that
where
B
represents
the
current boundary
of the
solid
to be
constructed.
Vis-
ibly,
such
a
coefficient
can be
considered
as a
measure
of the
"flatness"
of the
tetrahedra belonging
to the
boundary
of the
current solid.
Assuming
that
a
positive threshold
(3
is
controlled interactively
by the
user,
Boissonat [29] suggests removing
some
of the
tetrahedra
with
a
coefficient
b(t)
greater
than
/3
from
the
initial
3D
Delaunay tetrahedralization.
The
originality
of the
method comes
from
the way the
tetrahedra
are
removed
from
the
current
solid:
•
Only
tetrahedra (and
the
triangles
and
edges
they
contain)
are
removed.
•
Only
the
tetrahedra
whose
removal
generates neither
a
modification
of the
topology
of the
current
solid
nor a
removal
of an
initial
data
are
removable.
Consequently,
at any one
time,
it is
forbidden
to
remove:
—
tetrahedra that
do not
share
any
face
with
the
boundary
of the
current
solid,
—
tetrahedra that
share
3 or 4
faces
with
the
boundary
of the
current
solid,
and
—
tetrahedra that
share
a
face,
and
thus
3
vertices,
with
the
boundary
of
the
current
solid,
but
whose
fourth
vertex
is
itself
on the
boundary
of
the
solid.
Contrary
to
a-shapes,
the
objects
so
generated
have
a
constant
topological
dimension equal
to 3 and can be
considered
as
consistent objects
that
can be
used
as
discrete
models.
We
propose
calling
these
objects
/3-shapes.
CHAPTER 3. TESSELLATIONS

3.3.
NON-DELAUNAY TRIANGULATED SURFACES
109
Figure
3.8
Triangulation
of 3D
non-planar closed curves: series
of
links
are
determined
to
decompose
the
curves
into
more
or
less planar adjacent loops.
3.3
Non-Delaunay
triangulated surfaces
As
we
will
see in
chapter
6,
triangulated surfaces play
a
central
role
in the
modeling
of the
subsurface.
For
this reason,
it is
important
to
have
a
large
set
of
methods allowing initial versions
of
these surfaces
to be
built
from
rough
data.
The
Delaunay's tessellation presented
in the
previous section
is a
very
efficient
tool,
but
this method
is
applicable only
if the
surface
to be
built
is a
part
of a
plane.
For
this reason,
we
present
in
this section some
new
methods
that
do not
suffer
from
this limitation
and are
particularly well
adapted
to
geological
problems when
the
surface
to be
built
is
defined
by its
boundary:
• the
"patch
algorithm" corresponds
to the
case where
the
surface
to be
built interpolates
a 3D
closed curve
(see
figure
(3.8)),
• the
"strip algorithm" corresponds
to the
case where
the
surface
to be
built
interpolates
two 3D
open curves
(see
figure
(3.9)),
• the
"skin algorithm" corresponds
to the
case where
the
surface
to be
built
interpolates
two 3D
closed curves
(see
figure
(3.12)),
and
the
"pants algorithm" corresponds
to the
case where
the
surface
to be
built interpolates
one
series
of 3D
closed curves correlated with
another
series
of 3D
closed curves
(see
figure
(3.15)).

110
CHAPTERS.
TESSELLATIONS
3.3.1
Patch
Algorithm
Formulating
the
problem
As
shown
in figure
(3.8),
let us
consider
a
closed
3D
polygonal curve
C(P),
denned
by an
ordered
set of M
vertices assumed
to be
numbered
2
as
follows:
By
definition,
any
method allowing
a
triangulated surface
T
whose boundary
is
identical
to
C(P)
to be
built,
is
called
a
"patch
algorithm:"
In
practice,
we
have
to
consider
two
cases:
• If
C(P}
is
planar
and is not
self-intersecting, then
a
natural solution con-
sists
in
using
the
planar closed curve
Delaunay's
tessellation
algorithm
presented
on
page 105.
• If
C(P)
is a not a
planar curve
or is
self-intersecting,
then
it has to be
subdivided into
a
series
of
approximately
planar,
not
self-intersecting,
adjacent closed curves
to
which
the
planar Delaunay's tessellation algo-
rithm
can be
applied.
A
recursive
subdivision
algorithm
Let
"P(g,
n) be a
plane orthogonal
to the
unit vector
n and
containing
the
point
g:
• The
orthogonal
projection
TT(X)
of any
point
x
£
JR
3
on
"P(g,
n) is
such
that
and we
note
P*
the
orthogonal
projection
of P
onto
"P(g,
n):
•
Conversely,
the
original
p(i)
G P of any
point
7r{p(i)}
G P*
will
be
noted
as
T°{P*(*)}
Based
on
these notations,
it is
proposed using
the
following
recursive "patch
algorithm"
to
build
a
triangulated surface
T
honoring
the
constraint (3.5):
2
We
recall
that
the
notation
(o%b)
represents
the
rest
of the
division
of a by b.

3.3.
NON-DELAUNAY
TRIANGULATED
SURFACES
//—
Patch algorithm
void
Patch(
C(P),
T ){ //-
Patch
algorithm
//
//-
input
C(P)
=
closed
3D
polygonal curve
//—
output
T
=
triangulated
surface
honoring
(3.5)
•
look
for an
optimal plane
"P(g,
n)
such
that
P*
=
TT(P)
=>
C(P*)
~
C(P)
• M = P //-
number
of
vertices
of P
•
dmm
<
hOO
•
?"min
*
-L
•
Jmin
*
J-
for(
i
=
l;i<M;i
+ +) {
for(
j = i + 1
•
j < M ; j + + ) {
if({p*(z),p*(z
+
l)}n{p*(j),P*(j
+
l)}
^
0 ) {
•d=||p*(t)-P*U)ll
if(
d
<
d
m
i
n
) {
*
dmin
*
d
*
1min
*•
1
A
/i
.
^
i
*
Jrrnn
*
J
}
If-
end if
} //-
end
if
} //- end for j
}
//-
end for i
II
if(
imin
==
—1
) {
//~£(P*)
does
not
self-intersect
• T
<—
Delaunay's tessellation
of
C(P*)
(see
page
105)
•
reset each node
of
<9T
=
C(P*)
to its
initial location
in 3D:
p*(i)
—
7r°(p*(*))
Vp*(i)eP*
• set
DSI
Control-Nodes
on P*
•
apply
DSI to T to set the
location
of
internal nodes
}
else
{
• as
shown
in figure
(3.8), split
C(P)
into
two
closed curves
C(P')
and
C(P")
sharing
(p(i
m
m),p(jmin))
as
common edge
•
Patch(
C(P'),T'
)
•
Patch(
C(P"),T"
)
• T
<—
T'
U T"
}
//-
end
if_else
} //-
end
Patch
Looking
for an
optimal plane
P(g,
n)
The
patch
algorithm
presented
above
only
works
well
if an
"optimal"
plane
"P(g,
n) can be
found
such
that
In
practice,
we
suggest
proceeding
as
follows:
111

112
•
Define
gj
and ii as
gj
=
center
of
gravity
of
(p(i),
p(i
+
1))
li
=
||p(*
+
l)-p(t)||
•
Choose
g as the
center
of
gravity
of the set of
points
{g^}
weighted
by the
{li}
coefficients:
It is
possible
to
check
that
g so
defined
is the
center
of
gravity
of the
curve
C(P}.
•
Choose
n as the
eigen vector
associated
with
the
smallest eigen value
of the
3x3
symmetrical matrix
C
defined
by
We
will show herein below
that
such
a
choice
for g and n is
optimal
in the
following
sense:
Proof
According
to the
definition (3.6)
of
TT(-),
we
have:
i
If
we
want
to
minimize
X\^
•
||g^
—
^(gJI)
2
under
the
constraint
||n||
2
= 1,
then
we
have
to
look
for the
optimum
of the
following
function
where
A is a
Lagrange
multiplier (see [141,
90,
163]):
The
optimum
of
£(u)
is
achieved when
its
vectorial derivative vanishes
(see
page 147):
In
other words,
the
optimal choice
for n
corresponds
to an
eigen
vector
of C
associated
with
the
eigen value
A:
CHAPTER 3. TESSELLATIONS
3.3.
NON-DELAUNAY TRIANGULATED SURFACES
113
Figure
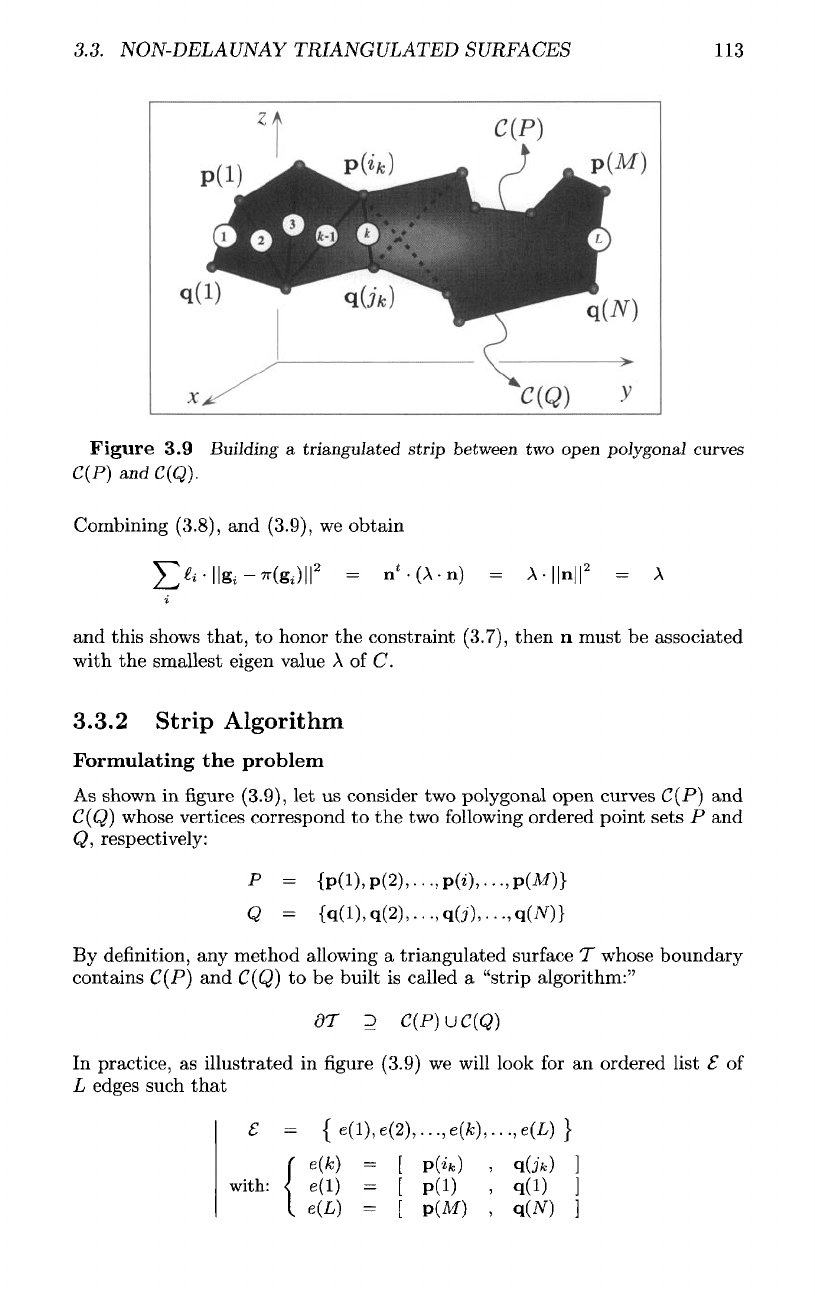
3.9
Building
a
triangulated
strip
between
two
open
polygonal
curves
C(P)
and
C(Q).
Combining (3.8),
and
(3.9),
we
obtain
and
this shows
that,
to
honor
the
constraint
(3.7),
then
n
must
be
associated
with
the
smallest
eigen value
A of C.
3.3.2
Strip
Algorithm
Formulating
the
problem
As
shown
in figure
(3.9),
let us
consider
two
polygonal open curves
C(P]
and
C(Q)
whose vertices correspond
to the two
following
ordered point
sets
P and
<5,
respectively:
By
definition,
any
method allowing
a
triangulated surface
T
whose boundary
contains
C(P]
and
C(Q)
to be
built
is
called
a
"strip
algorithm:"
In
practice,
as
illustrated
in figure
(3.9)
we
will
look
for an
ordered list
£ of
L
edges such
that

114
Moreover,
to
obtain
a
triangular mesh,
we
impose
the
following
constraints:
With
such
a
constraint,
for k < L,
each edge
e(k)
can be
associated with
a
triangle
T(k)
such
that
To
obtain "nice" triangles,
it is
wise
to
introduce
the
following
additional
constraint:
The
union
of all the
triangles
T(k)
so
defined
constitute
a
simply connected
triangulated
surface
T(«S):
As
suggested
in figure
(3.9),
this triangulated surface
T
looks
like
a
rectangular
strip
of
triangles limited
by a
polygonal boundary
<9T
such
that
In the
following
paragraphs,
we
propose
to
determine
an
optimal list
of
edges
£
respecting
the
constraints (3.10),
and
(3.11).
For
this purpose,
we
present
a
dynamic programming method similar
to
those proposed
by
[86,
43, 51,
41].
Dynamic
Programming
approach
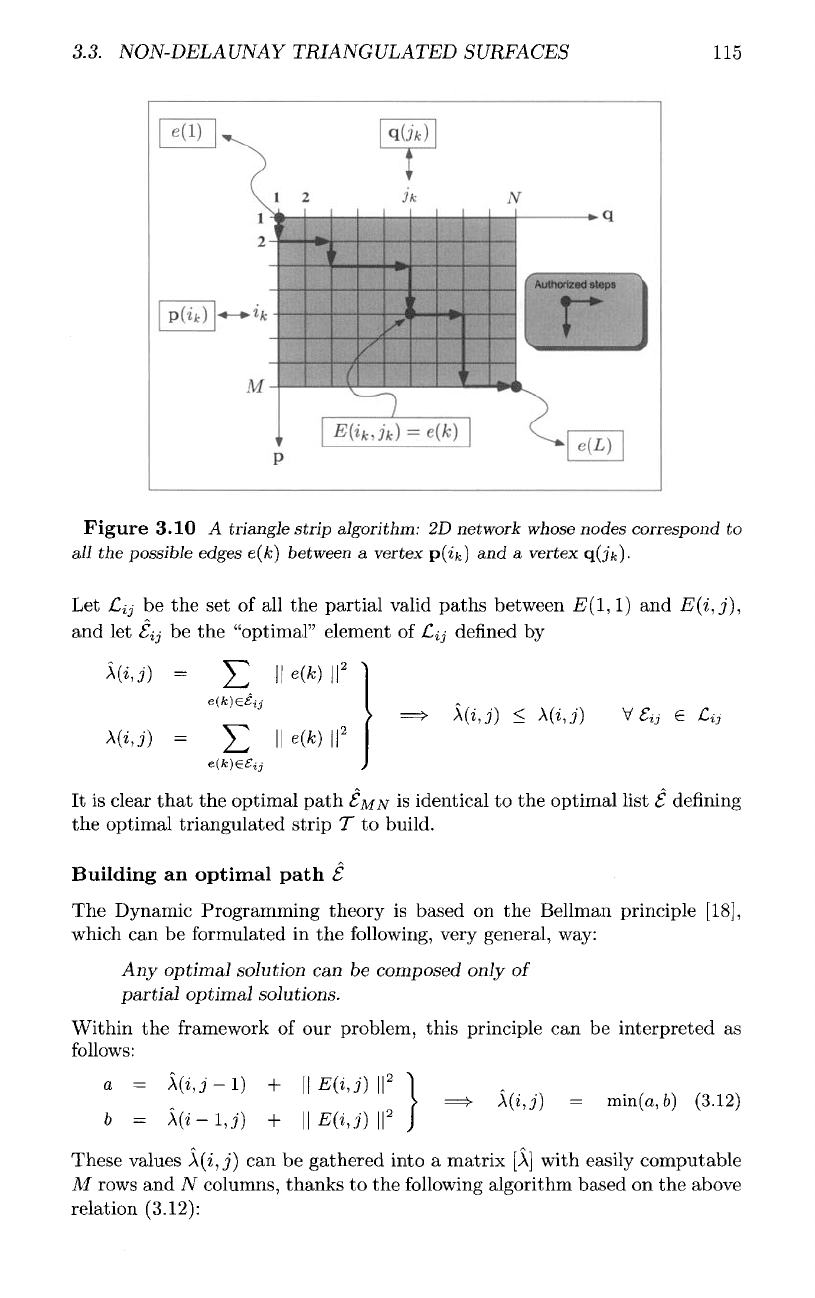
As
shown
in figure
(3.10),
the set of all the
possible edges
e(k)
can be
repre-
sented
by a 2D
rectangular network
E
with
M
rows
and
TV
columns
and
with
nodes
E(i,j)
such
that
Each list
£
corresponds
to a
path
in the
network between
the
nodes
.E(l,
1)
and
E(M,N);
according
to the
constraint (3.10),
any
valid
path
corresponds
to a
series
of
rightward
and
downward
steps
between
E(l,
1) and
E(M,
N}:
3
Note
that
the
criterion
||e(fc)||
2
can be
replaced
by
many other possible criteria such
as, for
example,
the
length
||e(A;)||
or the
area
of the
triangle generated (see Meyers
[161]).
In
practice,
all
these criteria
give
similar results.
CHAPTER 3. TESSELLATIONS
3.3.
Figur e
3.10
A
triangle
strip
algorithm:
2D
network
whose
nodes
correspond
to
all
the
possible
edges
e(k]
between
a
vertex
p(ik)
and a
vertex
q(jfe)-
Let
jCij
be the set of all the
partial valid paths between
E(l,
1) and
E(i,j],
and let tij be the
"optimal" element
of
Lij
denned
by
It is
clear
that
the
optimal
path
SMN
is
identical
to the
optimal list
8
denning
the
optimal triangulated
strip
T to
build.
Building
an
optimal
path
£
The
Dynamic Programming theory
is
based
on the
Bellman principle [18],
which
can be
formulated
in the
following,
very general, way:
Any
optimal solution
can be
composed only
of
partial optimal solutions.
Within
the
framework
of our
problem, this principle
can be
interpreted
as
follows:
These
values
A(i,j)
can be
gathered
into
a
matrix
[A]
with easily computable
M
rows
and N
columns, thanks
to the
following
algorithm based
on the
above
relation (3.12):
NON-DELAUNAY TRIANGULATED SURFACES
115

116
Figure
3.11
Part
(A)
shows
a
triangulated
surface
bridging
two
open curves.
Part
(B)
shows
the
same
surface after
applying "resampling"
and
"beautifying"
algorithms.
Once
the
matrix
[A] has
been computed,
it is
possible
to
build
the
optimal
list
£
using
the
following
iterative algorithm, which
is a
straightforward con-
sequence
of the
Bellman principle (see equation
(3.12)):
In
the
above program,
the
operation
a 0 b
represents
the
list resulting
from
the
concatenation
of two
lists
a and b.
CHAPTER 3. TESSELLATIONS

3.3.
NON-DELAUNAY TRIANGULATED SURFACES
117
Figure
3.12
Building
a
triangulated
surface
(skin)
between
two
closed
3D
curves.
Taking
links
into
account
It may be
that
we
want
to
constrain
the
triangulated surface
T
generated
by
the
above
strip
algorithm
to
honor
a
given edge link,
for
instance,
{p(i),
q
(.?')}•
In
this
case,
to
honor such
a
constraint,
the
only
possibility
is to
split
the
initial problem into
two
subproblems associated with
the two
pairs
of
curves
{C(P)i,C(Q)i}
and
{C(P)
2
,C(Q)
2
}
such
that
Example
Figure
(3.11)-A
gives
an
example
of a
triangular
strip
between
two
open
3D
curves.
The
resulting triangulated surface
presents
very skewed
triangles
and,
would
benefit
from
being
"resampled"
and
"beautified" (see sections
(6.6.2),
and
(6.6.1))
to
achieve
a
better triangulation, similar
to the one
shown
in
figure
(3.11)-B.
Comment
It
should
be
noted
that
the
"strip" algorithm presented above
can
also
be
viewed
as a
tool
for
automatically correlating
two
curves
of the 3D
space.
For
example, this algorithm
can be
used
for
correlating
the
curves contained
in
a
pair
of
non-intersecting surfaces corresponding
to
geological cross sections.
This
is
particularly interesting
in the
development
of an
algorithm able
to
build automatically
a 3D
cellular model
from
a
series
of
cross sections (see
[155]).
