Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


468
CHAPTER
9.
STOCHASTIC
MODELING
Figure
9.5
Graphical user
interface
of
a
3D-variogram
analyzer.
The
well
data,
with
the
faulted regular curvilinear
3-grid
covering
the
studied domain
in the
(x,
y,
z)
"geologic"
space,
are
mapped
onto
a
unit cube
in the
(11,
v,
w)
parametric space.
In
the
parametric space, faults vanish
and
ID-variograms
are
adjusted
in
some selected
directions. These ID-variograms
are
then
used
for
adjusting
a
range ellipsoid
and
a
3D-variogram
that
respects
a
chosen theoretical variogram model
specified
in the
"control
panel."
9.3.5
Cdf
s of an RF
As
in the
case
of the
moments
of an RF
Z(u,
w),
each
of the
variables
u
and
u>
induces
a
specific definition
of the
notion
of
cumulative
distribution
function
(cdf):
•
when
u is fixed, the
distribution
of the
values
z =
Z(u,
o>)
is
characterized
by
a
"statistical"
cdf or,
more simply,
the
"cdf"
at
location
u;
•
when
o>
is fixed, the
distribution
of the
values
z =
Z(u,
o>)
is
characterized
by
a
"spatial"
cdf.
Statistical
cdf
If
u is fixed in
D,
then
Z(u,
a;)
becomes
an
ordinary
RV
Z\^(uj}
—
Z(u,
u))
with
a
statistical
cdf
FZ
U
(Z)
that
is an
ordinary
function
-F"z(u;
z)
of the
variable
z G
JR
defined
as
Similarly,
if two
points
ui
and
112
are fixed in
D,
then
the RF
Z(u,
a;)
induces
two
RV's
Zu!
and
Z\i
2
having
a
joint
cdf
F
ZiZ2
(zi,
z^)
that
is an
ordinary

9.3.
RANDOM FUNCTIONS
function
FZ(UI,
112;
^1,^2)
of the
variables
z\
€
JR
and
z-2
6
JR
denned
as
More generally,
for any set of
sampling points
(ui,...,
UTV},
it is
possible
to
define
the
joint
cdf
FZ(UI,
...,
ujv;
^i,
•
•.,
ZN)
in a
similar way.
The
derivatives
of
these
functions,
when they exist,
are
called
the pdf of
the
RF:
If
H(s]
represents Heaviside's step
function
denned
by
then
it can be
written:
18
The
definitions
of
spatial
cdf s
presented
in the
next section
are
directly
in-
spired
by
these integrals.
Spatial
cdf
If
uj
is fixed in
15,
then
Z
w
(u)
=
Z(u,u;)
becomes
an
ordinary
function
of u
whose
spatial
cdf
F^(cu;
z]
is a
random
function,
as
defined
by
Similarly,
the
joint spatial
cdf
F
z
(u},
h;
z\,
z^)
is a
Random Function,
as de-
fined by
The
derivatives
of
these
functions,
when they exist,
are
called
the
spatial
densities
of the RF
Z(u,
w):
18
Remember
that
IP
(IS)
= 1:
this apparently useless term
is
added here purely
for the
sake
of
symmetry with
the
definition
of the
notion
of
spatial
cdf
(see equation
(9.51)).
469

470
CHAPTER
9.
STOCHASTIC MODELING
Estimating
cdf's
Let us
consider
a
random
function
Z(u,u))
defined
on (D x 0) and
observed
on a
finite
subset
(D*
x
15*)
such
that
Assuming
that
D* and
13*
are
uniformly
distributed
19
on D and
15,
respec-
tively,
equations
(9.50)
and
(9.51)
can be
used
as
follows
for
approximating
both
the
statistical
and
spatial
cdf's
of
Z(u,
a;):
There
are two
cases
to be
considered:
•
There
are a few
situations where
13*
contains more than
one
statistical
event:
for
example,
in
meteorology when
Z(\ii,Uj)
represents
the
temperature
ob-
served
at
location
Ui
at
time
ujj.
In
this case, both
the
statistical
and the
spatial cdf's
can be
estimated reasonably well thanks
to the
above expres-
sions.
•
Most
of the
time,
13*
is
reduced
to one
statistical event
WQ
meaning
that
all
that
can be
done
is to
estimate
the
spatial
cdf
FZ(WQ;
z)
associated with
this
unique
statistical event.
In
this case,
it is
common practice
to
assume
ergodicity
(see page 462)
to
identify
the
statistical
and
spatial cdf's:
Whatever
the
case,
the raw
approximations
F£(u^;
z) and
F^(ujj]
z) are
typi-
cally
replaced
by
smooth parametric equations
FZ(U;
z) and
Fg(u);
z)
approx-
imating
FZ(UJ;
z) and
F^*(UJJ;Z).
Normal
score-transform
Let
FZ(U',
z) be the cdf of a
random
function
Z(u,u).
By
definition:
• the
"normal score-transform," noted
as
$z(u;z),
is the
function
associated
with
Z(u,
a;)
and
denned
by
where
N(x
0,1)
is the cdf of the
centered
and
normalized Gaussian
law
(see
definition
(9.14)).
19
In
practice,
this
may not be the
case:
in
geology,
the
observed
data
are
often
clustered
on
well-paths
or
seismic lines,
and it may be
necessary
to
apply
a
"declustering"
technique.

9.3.
RANDOM FUNCTIONS
• the
"normal score"
of
Z(u,o>),
expressed
as
Z(u,
o>),
is the
random
function,
as
denned
by
According
to the
score-transform theorem (see equation
(9.18)),
F^(u;z)
is
indeed
a
centered
and
normalized Gaussian law:
Due
to the
very congenial properties
of the
multivariate Gaussian Random
Variables mentioned
on
page 452,
it is
common
geostatistical
practice
to
pro-
ceed
as
follows:
1.
Estimate
FZ(U;Z)
from
the
sampled
data
{Z(ui,uij)}
(see
preceding section)
and
build
the
associated normal score-transform
$z(u;
2),
2.
Transform
all the
sampled
data
{Z(\ii,Uj)}
into their normal score:
3.
Assume
that
{Z(ui,o;j)}
are a
sample
of a
multivariate Gaussian random
function
Z(u,
u;),
4.
Take advantage
of the
properties
of the
multivariate Gaussian Random Vari-
ables
(see
page
452)
for
realizing some operation
CL
on
Z(u,u>):
5.
Back
transform
the
result:
Section
(9.7.5)
shows
an
example
of
this strategy.
9.3.6
Tutorial examples
The
"pool"
example
In
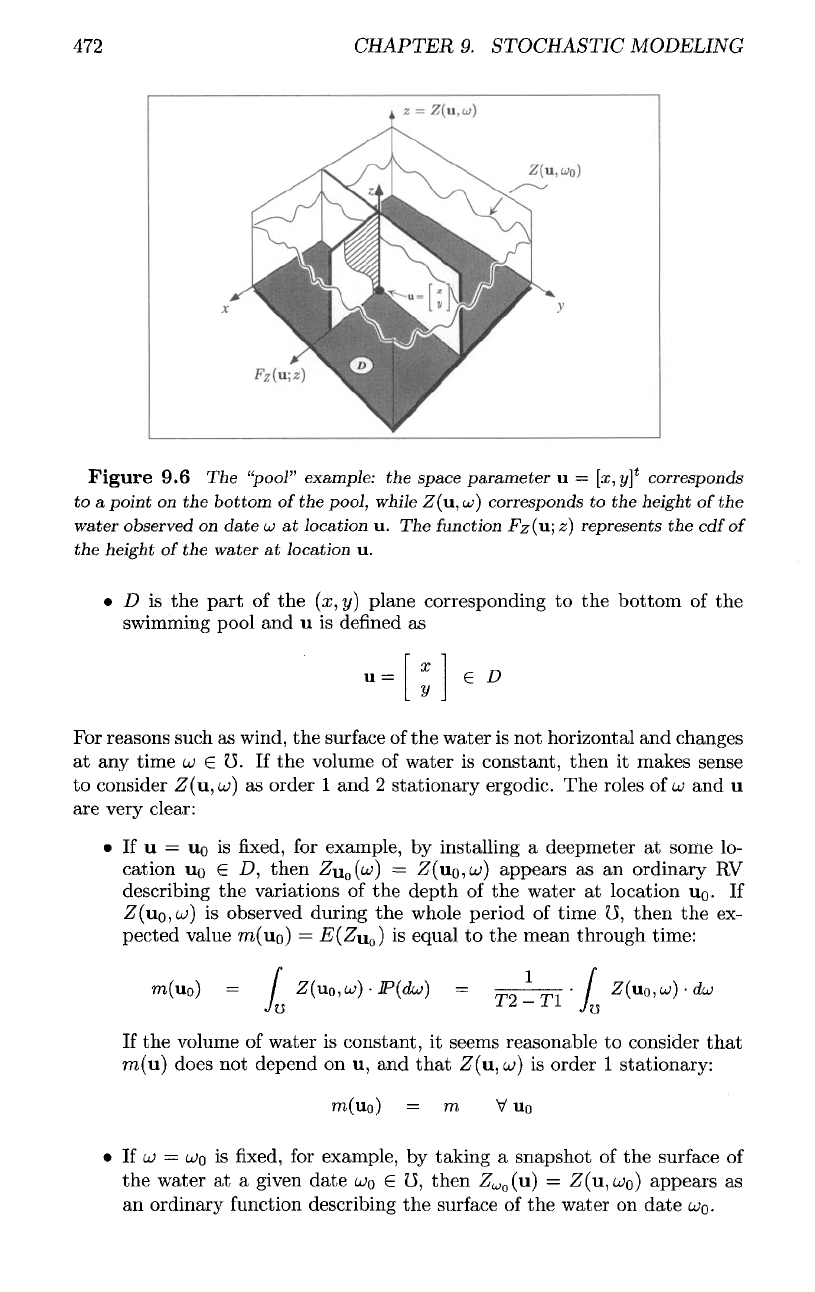
figure
(9.6),
Z(u,
uj)
is the
height
of
water observed
at
point
u of a
swimming
pool
on a
time
uo.
In
this case:
•
15
=]Ti,T
2
]
is the
period
of
time during
which
the
surface
of the
water
was
under observation.
• A is the
family
of all the
periods
of
time
A
=]£i,
£2]
contained
in
O.
•
IP
is
denned
as
471
472
CHAPTER
9.
STOCHASTIC MODELING
Figure
9.6 The
"pool"
example:
the
space
parameter
u
=
[x,
y]*
corresponds
to a
point
on the
bottom
of
the
pool,
while
Z(u,
u;)
corresponds
to the
height
of
the
water
observed
on
date
ui
at
location
u. The
function
Fz(u;
z)
represents
the
cdf
of
the
height
of
the
water
at
location
u.
• D is the
part
of the
(x,
y)
plane corresponding
to the
bottom
of the
swimming
pool
and u is
defined
as
For
reasons such
as
wind,
the
surface
of the
water
is not
horizontal
and
changes
at any
time
u;
€
O.
If the
volume
of
water
is
constant, then
it
makes sense
to
consider
Z(u,
a;)
as
order
1 and 2
stationary ergodic.
The
roles
of
a;
and u
are
very clear:
• If u =
UQ
is fixed, for
example,
by
installing
a
deepmeter
at
some
lo-
cation
u
0
6
£),
then
Z
Uo
(u>)
=
Z(UQ,UJ)
appears
as an
ordinary
RV
describing
the
variations
of the
depth
of the
water
at
location
UQ. If
Z(UQ,OJ)
is
observed during
the
whole period
of
time
13,
then
the ex-
pected value
ra(uo) =
E(Z\i
0
}
is
equal
to the
mean through time:
If
the
volume
of
water
is
constant,
it
seems reasonable
to
consider
that
m(u)
does
not
depend
on u, and
that
Z(u,
o>)
is
order
1
stationary:
• If
(jj
=
LJQ
is fixed, for
example,
by
taking
a
snapshot
of the
surface
of
the
water
at a
given
date
UQ
€
15,
then
Z
Wo
(
u
)
=
Z(U,UQ)
appears
as
an
ordinary
function
describing
the
surface
of the
water
on
date
UJQ.

9.3.
RANDOM FUNCTIONS
Figure
9.7
Comparison
of
the
"pool"
and
"linen"
examples.
Let
m
s
(ujQ}
be the
spatial mean value
on
date
UQ
defined
as
If
the
volume
of
water
is
constant
and if
m(u)
= ra
does
not
depend
on
u,
then
it
seems reasonable
to
consider
that
m
s
(cjo)
does
not
depend
on
UJQ
and to
assume
that
Z(u,
a;)
is
ergodic
so
that
The
"linen"
example
Let
us now
imagine
that
the
water
is
removed
from
the
pool
of our
previous
example
and the
surface
of the
water
is
replaced
by a
piece
of
linen covering
the
domain
D. To
constrain
the
linen
to
behave like
the
water's
surface,
the
following
procedure
is
proposed:
•
Install vertical poles located
at a set
D*
consisting
of N
sampling points
(ui,...,
Ujv}
belonging
to the
domain
D.
Each pole
has a
different
given
length
and the
linen
is fixed at the top of
each pole with
a
pin;
•
Install
a set of
electric
fans
above
and
below
the
linen
so
that
the
shape
of
the
linen
can be
modified
through time.
By
so
doing,
the
linen
can be
considered
as an RF
Z(u,
a;)
exactly like
the
surface
of the
water
in the
case
of the
pool example. However,
as can be
seen
in figure
(9.7),
there
is an
important
difference:
the RF
Z(u,o;)
is now
constrained
at the
TV
points
{u^}
and
degenerates into deterministic values
{z(ui)}
at
these points. Consequently,
the cdf
F
Zu
_(z)
at a
point
u^,
where
473

474
CHAPTER
9.
STOCHASTIC MODELING
Z(u,u>)
is
constrained
to be
equal
to the
length
z(ui)
of the
corresponding
pole,
degenerates into
a
step
function
such
that
Stochastic
blending
of
ordinary
functions
Let
{/i(u),...,
/
n
(u)}
be a
series
of
ordinary functions where
u is a
vector
of
a
parametric space
t
=
M
p
and let
{/?o(u;),...,
/?
n
(u;)}
be an
associated series
of
"blending" Random Variables
defined
on a
probabilized space
(15,
A,
IP).
Prom
these
two
series,
it is
always possible
to
build
an RF
2T(u,
a;)
defined
as
follows:
This example
is at the
origin
of a
very important
family
of
RF's called "Ran-
dom
Fourier Series"
and
presented
in the
next section.
We
will
see
also
in
section (9.8)
how
such stochastic blendings
of
ordinary
functions
can be
used
for
generating RF's honoring
a
given mean
and a
given variogram.
9.4
Random
Fourier
Series
It is
well
known (e.g.,
[15])
that
any
periodic integrable
function
z(u)
having
a
period equal
to
2?r
on
1R
can be
approximated
by a
Fourier Series
z(u)
as
defined
by
where
the
coefficients
{zf,}
and
{z%.}
are
such
that
This
suggests
that
any
random function
Z(u,u;)
whose realizations
are
peri-
odic
integrable functions
of u on
[0,2?r]
can be
approximated
by a
Random
Fourier
Series
(RFS)
Z(u,u)
defined
as

9.4.
RANDOM FOURIER SERIES
where
the
Random Variables
{Z£(u;)}
and
(Z^(cj)}
are
such
that
Let
us
assume
that
Z(w,
a;)
is a
centered Gaussian second-order stationary
random
function with known mean
and
covariance:
Z(u,u>)
is a
Gaussian Random Variable
V u
with:
The
next section addresses
the
problem
of
building
the
Random Variables
{Z^(uj}}
and
{Zf,(<jj}}
in
such
a way
that
Z(u,
u>)
is a
Gaussian Random Variable
V u
with:
It
will
also
be
shown
how the
decomposition
(9.54)
can be
generalized when
u is a
vector
of
IR
P
.
9.4.1 Building
a
stationary one-dimensional
RFS
Let
{Z}.,Zf.
:
k =
0,1,...,
K —
1}
be a
family
of
independent
Random
Variables such
that
Let
us now
consider
the
periodic random
function
Z(u,u}
denned
as
follows
for
any
value
of the
parametric space variable
u
e
[0,
2?r]:
From
properties
(9.56),
it can be
deduced
that
the
mean value
and the Co-
variance
function
of
Z(w,
a;)
must
be
such
that
475

476
CHAPTER
9.
STOCHASTIC
MODELING
In
other words,
Z(u,
uj}
is a
centered second-order
stationary
random function
having
a
stationary covariance function
C^(h)
as
defined
by
where
h
represents
a lag in the
range
[—2?r,
+2yr].
The
only parameters
denning
Z(u,uj)
are the
coefficients
{cr
2
,}
and the
degree
K of the
polynomials used
in
equations
(9.56)
and
(9.57).
In
practice,
the
coefficients
{cr
2
}
are
chosen
to
have
where
cov(h)
is a
given
"target"
one-dimensional stationary covariance
func-
tion (see page 464) assumed
to
capture
the
"style"
20
of the
random
function
Z(u,u})
to be
built.
Comparing
equations
(9.58)
and
(9.60)
enables
us to
write
This suggests [144] interpolating
the
given function
cov(h)
by the
trigonomet-
ric
polynomial
{^fcJo
a
fc
'
cos
(kh)}-
For
example,
if we
choose
to
interpolate
the
series
of
points
{hj}
belonging
to ]0,
TT]
such
that
then,
for
any
21
pair
of
integers
p and q
lower
or
equal
to K — 1, the
following
orthogonality relationships hold true (see
[129]):
From these,
the
following
values
22
for
{cr
2
}
can be
deduced
where
the
family
of
functions
</>#(&,
h]
are
defined
by
20
See
section
(9.4.6)
21
More
precisely,
for any p and q
modulo
2 •
K.
22
Note
that
the
values
{cr
2
,
cr
2
,...,
&
2
K
_i\
correspond
to the
discrete
cosine
transform
(see
[93])
of the
function
cov(h).
As a
consequence,
one can
think
of
using
the
"fast"
discrete
cosine
transform
for
computing
these
values.

9.4.
RANDOM FOURIER SERIES
477
It can be
shown
that
these values
(a)?}
are
always positive provided
that
the
given
covariance
function
cov(h)
honors
the two
following
conditions:
From equations (9.61)
and
(9.62),
we can
also deduce
that
The
parameters
defining
the
one-dimensional random
function
Z(u,uj}
pre-
sented above
are now
reduced
to the
degree
K and the
covariance
function
cov(h)
of the
trigonometric polynomial
Z(u,uo}.
In
practice, these parameters
can be
chosen
as
follows:
• The
covariance
function
cov(h)
is
assumed
to
depend only
on a
"range"
23
parameter
R,
which
is
determined
from
a
"prior" knowledge
of the
"style"
24
of the
random
function
Z(u,u).
As
shown
in figure
(9.8),
—
a
short
range, typically
R <
^5,
yields
an
erratic
style
for the
random
function
Z(ii,u;),
and
—
a
large range, typically
R >
77,
yields
a
smooth
style
for the
random
function
Z(u,
uj).
•
Degree
K of the
polynomial must
be
large enough
to
obtain
a
good
ap-
proximation
of
equation (9.61).
For
this purpose,
the
following
strategy
inspired
by
equation
(9.64)
can be
used:
—
choose
a
large value
for
K,
say,
K
>
30,
—
choose
a
percentage
p,
say,
p =
80%,
and
determine
the
smallest
set
/C
of
indexes such
that
—
restrict
the sum
(9.57)
to the set
/C:
small coefficients
{crj.}
can be
disregarded
without having
to
recompute
25
the
remaining coefficients.
23
The
range
of
cov(h}
is
equal
to the
distance
h
beyond
which
cov(h]
can be
considered
as
equal
to
zero.
24
See
section
(9.4.6)
25
This
is a
consequence
of the
orthogonality relationships
(9.62).
