Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


448
CHAPTER
9.
STOCHASTIC MODELING
This
implies
that,
if
fz(z)
exists,
the
mean
mz
and the
variance
a\
can be
computed according
to the
following
formulae:
If
FZ(Z)
is not
derivable, then
a
formula similar
to
equations (9.6)
and
(9.7)
can be
obtained using
the
Stieljes-Lebesgue integrals
(see
[15]):
The
most simple example
of RV is the
(binary) indicator Random Variable
Z =
I
A
associated with
an
event
A of A
defined
as
The
following
straightforward relation always holds
for any
indicator
RV
I
A
'•
Moreover,
it can be
shown
that
any RV Z can be
approximated
by a
weighted
sum of
indicator Random Variables:
In
this sum,
{zi}
represents
a
series
of
real values, while
the
events
{Ai}
are
assumed
to
realize
a
partition
of
13.
9.2.3 Some
useful
examples
of
RV's
Uniform
Random
Variable
Let [a,
b]
be an
interval
on
JR.
An RV Z is
said
to be
"uniform"
on [a,
b]
if its
cdf
is
such
that
It can be
checked
that
the
associated
pdf
f
z
(z)
is
such
that

9.2.
PROBABILITIES
IN A
NUTSHELL
449
This
RV is
fully
defined
by the two
parameters
a and b or,
equivalently,
by its
mean
and
variance, which
are
The
inverse
function
U~
l
(p\a,
b) is a
linear
function
of p G
[0,1]:
Moreover,
the cdf
FX
(z) of any
continuous Random Variable
X can be
roughly
approximated
as
follows
by a
uniform
law
having
the
same mean
mx
and the
same variance
a\
as
X:
Similarly,
the
inverse
function
F
x
l
(p)
can be
roughly approximated
by
Gaussian
Random
Variable
Let
m
be a
real number
and
a
2
be a
positive real number.
An RV Z is
said
to be
"Gaussian"
or
"normal"
if its cdf is
such
that
The
associated
pdf
fz(z)
is
This
RV is
fully
defined
by its
mean
and its
variance
Useful
precise numerical approximations
of
F
z
(z]
and
F^
l
(p)
can be
found
in
[1].
Degenerated
Random
Variable
Let
m be a
real number.
An RV Z is
said
to be
"degenerated"
if its cdf is a
Heaviside
function,
as
denned
by
Note
that
the
degenerated
cdf
Ti.(z\m)
can be
viewed
as the
limit
of a
normal
cdf
J\f(z\m,
cr
2
)
when
the
variance
cr
2
tends
toward zero:
It can
also
be
viewed
as the
limit
of the
uniform
cdf
U(z\a,
b)
when
a and b
tend
simultaneously toward
m:

450
CHAPTER
9.
STOCHASTIC MODELING
9.2.4
Score-transform
theorem
A
famous theorem called
the
score-transform
theorem
states
that
the two
following
relationships
are
always true:
• For any RV
X,
the
transform
U =
Fx(X)
is
such
that
where
U(u\0,1)
is the
uniform
cdf on
[0,1].
The RV U
=
F
X
(X)
so
denned
is
called
the
uniform transform
of the RV
X.
•
Conversely,
if U is an RV
uniformly distributed
on
[0,1],
then,
for any
contin-
uous
cdf
F,
the
following
implication
is
true:
From equations (9.16)
and
(9.17),
the
"score-transform formula"
can be de-
duced
in a
straightforward way:
Proof
According
to
equation (9.5):
Applications
• The
property (9.17)

9.2.
PROBABILITIES
IN A
NUTSHELL
is
of
particular interest
in
simulation when
an RV Z
having
a
given
cdf
F(z]
has to be
generated.
In
such
a
case, using
a
random number
generator able
to
simulate
a
uniform
RV U
allows
Z to be
defined
as
Z =
F^
1
(U).
For an
example
of the use of
this property,
refer
to
section
(9.6).
•
More generally,
the
score-transform
formula
shows
that
any RV X can
be
transformed into
a RV Z
having
any
type
of
predefined continuous
cdf
F.
For an
example
of the use of
this property,
refer
to
section
(9.3.5).
9.2.5
Notion
of a
vectorial Random Variable
The
case
of a
pair
(Zi,
Z%}
of
Random Variables
Consider
a
pair
of
RV's
(Zi,Z
2
).
These
two
RV's
can be
considered
as the
components
of a
column matrix
or
vector
Z:
Such
an
application
from
U to
JR
is
called
a
"bivariate"
RV.
When they exist,
the
mean value
mz
and the
covariance matrix
[C
zz
]
are
defined
as
In
the
matrix
[C
zz
],
each term
C
z
.
z
.
is
called
the
covariance
of the
pair
(Zi,
Zj]
and is
defined
by
Note
that
the
variance
cr|.
defined
by
equation
(9.4)
is
such
that
The
notion
of
cumulative distribution
function
is
generalized
to
M
2
by the
following
formula:
From the definition (9.1) of JP, it can be shown that any bivariate cdf F
z
z
has the
following
properties:
When
F
ZiZ2
(zi,Z2)
is
derivable,
its
derivative
451

452
CHAPTER
9.
STOCHASTIC MODELING
is
a
nonnegative
function
called
the
Probability Distribution Function (pdf)
of
the
vector
Z. The
above definitions imply
the
following
relations where
f
z
(z\)
and
f
z
(22)
are
called
the
"marginal"
pdf
functions
relative
to z\ and
£2,
respectively:
Similarly
to the one
dimensional case,
it can be
shown
that,
for any
function
9(zi,
zz],
the
following
formula
of
transfer
is
valid:
Generalization
Let
us
consider
a
family
{Zi,Z%,...,
Z
N
}
composed
of N
RV's indexed
by an
integer
index
i G [1,
N].
These
RV's
can be
considered
as the
components
of
a
column matrix
Z:
Such
an
application
Z
from
13
to
M
N
is
called
a
vectorial
RV.
When they
exist,
the
mean value
m
z
and the
covariance matrix
[Czz]
are
denned
by
Note
that
[C
zz
]
is
symmetrical because
C
ZiZ
.
=
C
z
.
z
..
Moreover,
any
linear
combination
of the
components
of Z is a
(scalar)
RV Y
which
can be
written
as
It can
easily
be
checked
that
the
variance
dy
of
that
linear combination
is
then
a
quadratic
form:
This implies
that
any
covariance matrix
[C
zz
]
is
always semipositive
definite.
Multivariate
Gaussian
Random
Variable
By
definition,
a
Random Variable
Z =
[Zi,...,
ZN]*
with
a
mean value
mz
and a
covariance matrix
[Czz]
is
said
to be a
"multivariate
Gaussian" variable
if
its pdf
fz(z)
is
defined
by

9.2.
PROBABILITIES
IN A
NUTSHELL
In
practice,
multivariate
Gaussian Random Variables
are
characterized
by the
following
properties:
• any
submatrix
of Z is
also
a
multivariate Gaussian Random Variable;
• any
linear combination
of the
components
of Z is a
one-dimensional Gaussian
Random Variable;
• the
components
of Z are
independent
6
if, and
only
if,
[Czz]
is
diagonal,
that
is,
CziZj
= 0 for all i
^
j;
and
• for any
partition
of Z
into
two
submatrices
Z — [X,
Y],
the
conditional
distribution
7
fy/x(y\
x
)
of Y
when
X = x is fixed is
multivariate Gaussian.
9.2.6
Notion
of
independence
Definitions
• Two
events
Ai and Aj are
said
to be
.^-independent
or,
more simply
independent,
if the
following
relation holds true:
According
to
equation
(9.2),
the
independence
of Ai and Aj can
also
be
defined
as
follows:
{Ai
independent
of
Aj}
• By
definition,
two
RV's
Zi and Zj are
said
to be
independent
if the
events
Ai
and Aj
are
independent
for any
a$
G
1R
and any
a,j
G
M.
Characterization
of
independent
RV's
Let
us first
observe
that
As
a
consequence,
the
following
characteristic property
can be
deduced
from
the
definition
of the
independence
of two
RV's:
{ Zi
independent
of Zj }
6
See
section
(9.2.6).
7
See
[139,
78,
159]
for a
formal definition
of the
notion
of
conditional distribution.
453

454
CHAPTER
9.
STOCHASTIC MODELING
If
FZ^J
(
z
ii
z
j)
is
derivable relative
to Zi and
Zj,
then
it can be
deduced
that,
for
any
pair (zi,
Zj\
the
following
properties also hold true:
{ Zi
independent
of Zj }
Moreover,
if Zi —
1^
and Zj =
IA^
are two
indicator Random Variables (see
definition
(9.9)),
then
the
following
property
is a
straightforward consequence
of
the
definitions
(9.3)
and
(9.21):
{ Zi
independent
of Zj
From equation
(9.10),
it can be
deduced
that
this property
is
also true
in the
general case where
Zi
and/or
Zj are not
indicator Random Variables.
Transformation
of
independent
RV's
The
following
property
is
true
for any
pair
{gi(z),gj(z)}
of
ordinary
functions:
8
{ Zi
independent
of Zj }
•<=>•
{
§i(Zi)
independent
of
gj(Zj)
}
(9.24)
In
this case,
the
Random Variables
{Zi,
Zj}
are
said
to be
"pairwise
indepen-
dent."
More
generally,
a
series
of n
Random Variables
{Zi,...,
Z
n
}
is
said
to be
stochastically independent
if, for any
series
{gi,...,
g
n
}
of
ordinary
functions,
the
following
equality holds:
E{
5l
(Zi)
•
9
2(Z
2
)
• •
•
g
n
(Zn)
} =
E{g
1
(Z
l
)}
•
E{g
2
(Z
2
)}
• • •
E{g
n
(Z
n
)}
(9.25)
Warnings
•
Pairwise independence
for all i
^
j as
defined
by
equation
(9.24)
does
not
implies
the
independence
of the
series
{Zi,..
.,Z
n
}
as
defined
by
equation
(9.25).
•
Care must
be
taken
not to
confuse
the
shape
of
cumulative distribution
functions
with
the
behavior
of the
associated RV's. There
is no
relation-
ship between
the
shape
of two
cumulative distribution
functions
and the
fact
that
the
corresponding RV's are,
or are
not, independent:
In
fact,
it is
possible
for two
independent RV's
to
have exactly
the
same
cdf.
Central
limit
theorem
Let
{Zi,
^2,...}
be a
series
of
Random
Variables
and let
SN
be the
associated
Random Variable,
as
defined
by
8
In
fact,
gi(z)
and
gj(z)
have
to be
measurable (see
[101]).
9.2.
PROBABILITIES
IN A
NUTSHELL
455
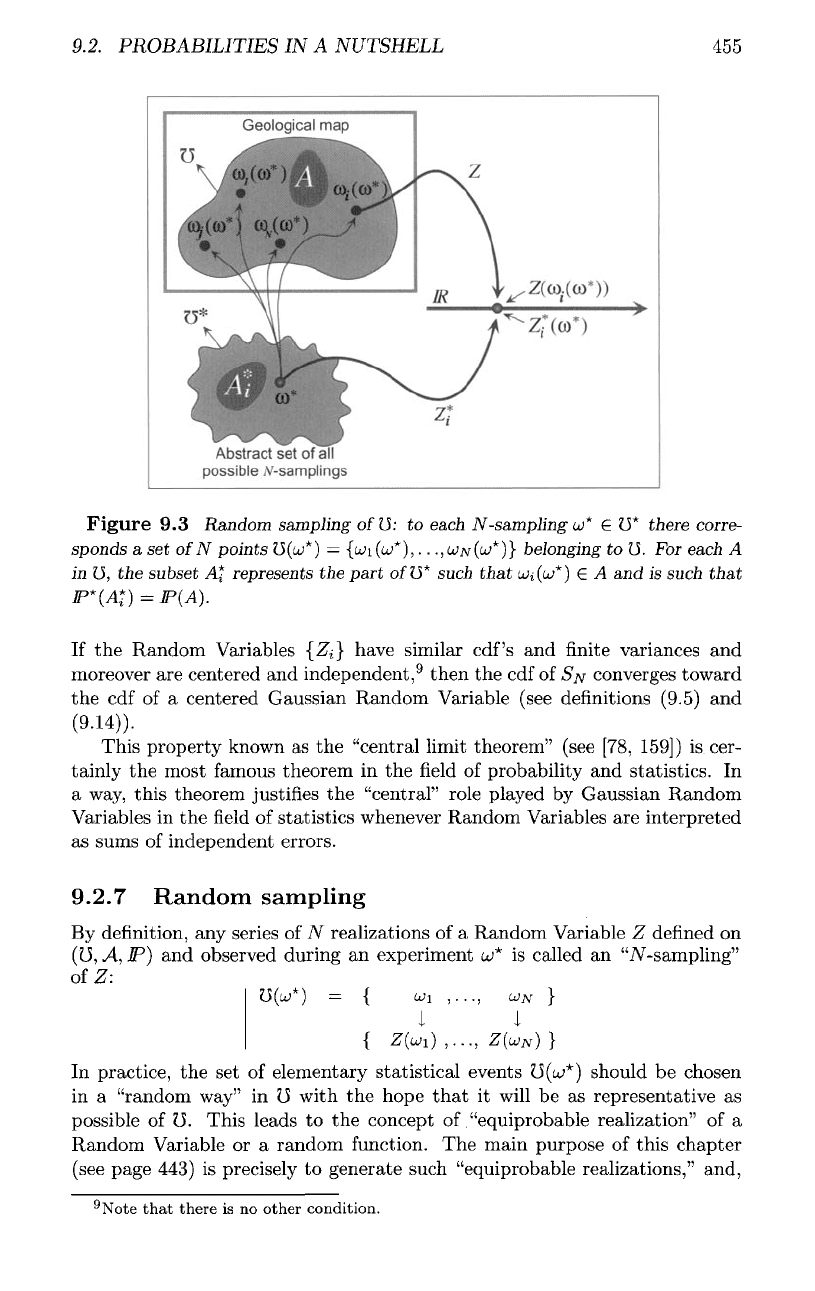
Figure
9.3
Random
sampling
of
15:
to
each
N-sampling
u>*
€
13*
there
corre-
sponds
a set
of
N
points
15
(u>*)
=
{u>i(uj*),..
.,UJN(U*)}
belonging
to
15.
For
each
A
in
15,
the
subset
A*
represents
the
part
of15*
such
that
u)i(u*}
£ A and is
such
that
IP*
(A*}
=]P(A).
If
the
Random Variables {Zi} have similar
cdf's
and finite
variances
and
moreover
are
centered
and
independent,
9
then
the cdf of
SN
converges toward
the cdf of a
centered Gaussian Random Variable (see definitions (9.5)
and
(9.14)).
This
property known
as the
"central limit theorem" (see [78,
159])
is
cer-
tainly
the
most
famous
theorem
in the field of
probability
and
statistics.
In
a
way, this theorem
justifies
the
"central" role played
by
Gaussian Random
Variables
in the field of
statistics
whenever Random Variables
are
interpreted
as
sums
of
independent errors.
9.2.7
Random
sampling
By
definition,
any
series
of N
realizations
of a
Random Variable
Z
defined
on
(U,
A,
IP]
and
observed during
an
experiment
a;*
is
called
an
"JV-sampling"
of
Z:
In
practice,
the set of
elementary statistical events
U(u;*)
should
be
chosen
in
a
"random way"
in 0
with
the
hope
that
it
will
be as
representative
as
possible
of
15.
This leads
to the
concept
of
"equiprobable realization"
of a
Random Variable
or a
random
function.
The
main purpose
of
this chapter
(see
page 443)
is
precisely
to
generate such "equiprobable realizations," and,
9
Note
that
there
is no
other
condition.

456
CHAPTER
9.
STOCHASTIC MODELING
as
such,
it is
worthwhile
to
define
this concept mathematically rather
than
to
rely
merely
on
intuition.
In
this section,
after
an
intuitive introduction,
a
formal
definition
of the
notion
of
"random sampling"
is
proposed
that
is at the
origin
of the
notion
of
"mathematical statistics." Prom
a
practical point
of
view,
we
will
also show
how
such samplings
can be
generated
on a
computer.
Random
sampling
of
13:
an
intuitive
definition
As
suggested
in figure
(9.3),
let us
consider
a
domain
13
corresponding
to
a
part
of a
geological
map
where
a
(potentially)
infinite
set
13*
of
companies
simultaneously
and
independently
of
each other decide
to
drill
N
wells.
10
The
triplet
(13,
A,
IP)
can
always
be
defined
as the
Probabilized Space associated
with
the
domain
13 in
such
way
that
A
contains
all the
parts11
of 13,
while
JP
is
defined
by
12
Accordingly,
a
series
of N
well
locations
{a>i(u;*),..
.,u;jv(<*>*)}
can be
asso-
ciated with each company
ui*
G
13*.
Intuitively,
it can be
said
that
these
well
locations constitute
a
"random sampling"
of 13
when
the two
following
conditions
are
honored:
1)
the
number
of
companies
that
have
chosen
to
install
their
ith
well
u>i(u*)
on any
given
part
A
of
13
is
proportional
to the
area
of
A,
that
is,
IP
(A),
2)
for any
subset
A of
13,
the
fact
of
installing
the ith
well
uji(u*)
on
A has no
influence
on the
possibility
of
drilling
other
wells
on
the
same
subset.
The
next section proposes
a
formalization
of
this notion
of
random sampling.
Random
sampling
of
13:
A
formal definition
Let
(13,
A,
IP)
be a first
Probabilized Space
and let
(13*,
A*,
IP*)
be a
second
Probabilized Space called
the
"space
of
samplings."
On the
other hand,
let
{13(uj*)
:
cu*
e
13*}
be a
family
of
discrete subsets
of
13
defined
as
follows:
By
definition,
it
will
be
said
that
{13(u*)
:
LJ*
e
13*}
is a
"random sampling"
of
13 if the
Probabilized Space
of
samplings
(13*,
A*,
IP*)
has
been chosen
in
function
of
(13,
A,
IP)
in
such
a way
that
the two
following
properties similar
to
(9.26)
conditions
are
honored:
10
For
example,
to
measure
the
depth
Z(uj)
of a
given horizon
denned
on
13.
11
Such
cr-algebra
is
called
the
"Lebesgue"
<r-algebra
of
15.
12
\A\
and
\13\
represent
the
area
of A and
15,
respectively.

9.2.
PROBABILITIES
IN A
NUTSHELL
If
this
condition
is
honored, then
the set
15(u*)
is
called
a
"realization"
of the
random sampling
of
13
and the
associated events
{uji(u>*},..
.,U>N(U*}}
are
said
to be
"independent."
Random
sampling
of an RV
Let Z be a
Random Variable
denned
on
(15,
A,
IP],
and let
15
(u*)
be a
ran-
dom
sampling
of
15
associated with
(£5*,.4*,
JP*).
On the
other hand,
and as
suggested
in
figure
(9.3),
let
{Z*,...,
Z^}
be the
series
of
Random Variables
denned
as follows on
(0*,
A*,
IP*):
By
definition,
{Z±,...,
Z^}
is
called
a
"random
Af-sampling
of
Z"
and
each
series
of
values
{Z*(u*},...,
Z~^(uj*}}
is
called
a
"realization"
of
this
N-
sampling.
It
will
also
be
said
that
are
independent realizations
of Z
As
a
direct
consequence
of
(9.5), (9.21),
(9.22),
and
(9.27),
it can be
shown
that
where
FZ*(Z)
and
FZ(Z)
are the
cdf's
of Z* and Z,
respectively.
Notion
of
statistic
By
definition,
a
"statistic"
on Z is any
Random Variable
T*
denned
on
(0*,
.4*,
IP*)
as a
(measurable)
function
of an
TV-sampling
of Z:
Among
the
most classic statistics,
one can
mention
the
notions
of
"experi-
mental mean"
M|
N
and
"experimental variance"
V£
N
,
as
defined
by
Using
properties
(9.29),
it can
easily
be
shown
that
457
