Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

428
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
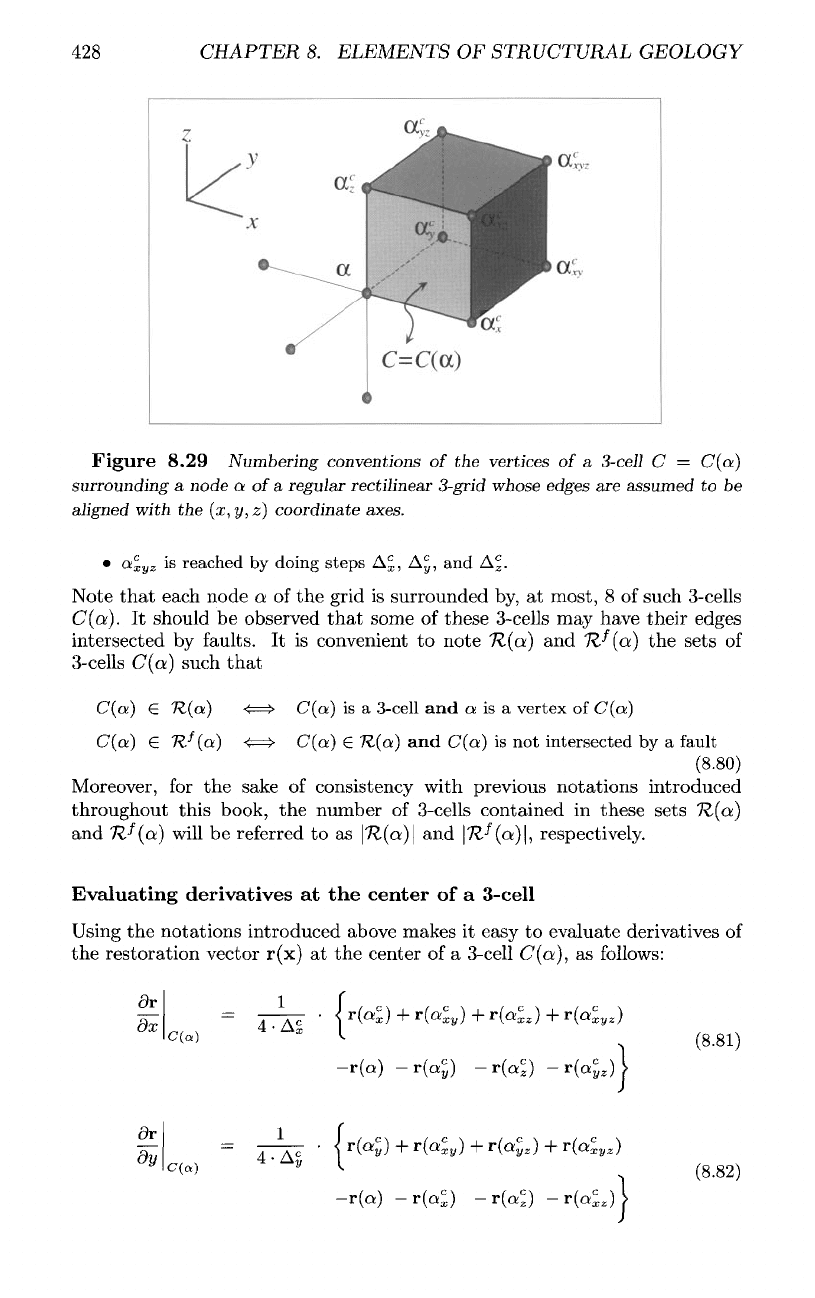
Figure
8.29
Numbering
conventions
of the
vertices
of a
3-cell
C =
C(a)
surrounding
a
node
a
of
a
regular
rectilinear
3-grid
whose
edges
are
assumed
to be
aligned
with
the
(x,y,z)
coordinate
axes.
•
Oixy
Z
is
reached
by
doing
steps
A£,
A£,
and
A£.
Note
that
each node
a of the
grid
is
surrounded
by, at
most,
8 of
such
3-cells
C(o).
It
should
be
observed
that
some
of
these
3-cells
may
have
their
edges
intersected
by
faults.
It is
convenient
to
note
7£(a)
and
l^J
(a) the
sets
of
3-cells
C(a)
such
that
Moreover,
for the
sake
of
consistency with previous notations introduced
throughout this book,
the
number
of
3-cells contained
in
these sets
7?.(a)
and
72/(o:)
will
be
referred
to as
\Jt(a)
and
|72/(o:)|,
respectively.
Evaluating
derivatives
at the
center
of a
3-cell
Using
the
notations introduced above makes
it
easy
to
evaluate derivatives
of
the
restoration vector r(x)
at the
center
of a
3-cell
C(a),
as
follows:

8.6.
UNFOLDING
A
STACK
OF
LAYERS
Evaluating
derivatives
at a
node
of the
grid
Taking
into
account equations (8.80), (8.81), (8.82),
and
(8.83) allows
the
derivatives
of
r(x)
to be
evaluated
at any
node
a and in any
direction
d
G
{x,
y,
z} as
follows:
8.6.4
Mass-Preservation constraint
Whatever
the
restoration method used
for
unfolding
the
layers,
the
mass
of
terrains
18
has to
remain
constant.
This
constitutes
the
fundamental principle
that
any 3D
restoration method
has to
conform
to and
corresponds
to the
continuity equation (8.73).
In the
following
it
will
be
shown
how
this equation
can
be
turned into
a
DSI
constraint.
For
simplicity's sake,
it is
implicitly assumed
that
the
tectonic deforma-
tions
are not so
severe
and
that
the
acceleration
5
2
X[
t
](a)/'dt
2
can be
ignored.
Accordingly,
the
continuity equation (8.73)
can be
reduced
to the following,
simpler
equation:
In the oil and gas
industry,
the top
horizon
is
generally moderately folded,
making
it
feasible
to use
this approximation. However,
in
severely
folded
geological structures,
the
acceleration
<9
2
X[
t
](a)/<9t
2
cannot
be
ignored
and
the
solution obtained when using
the
equation (8.85)
can
only
be
considered
as
a first-order
approximation.
Approximating
the
continuity
equation
Due
to the
compaction induced
by the
pressure
19
of
terrains, during
the
sed-
iment burial
and
diagenesis process
the
porosity
0(d)
decreases with depth
d.
In
practice,
the
following
empirical porosity/depth model
of
Magara
is
proposed [143, 196,
122]:
where
</>o
is the
initial porosity
at
depth
d = 0 and A is the
porosity decay
length
20
as
defined
by
18
The
volume
may
change
due to
compaction.
19
From
a
strict physical point
of
view,
the
porosity evolution versus depth depends
on
the
actual
pore
pressure
and not
only
on the
pressure
due to
burial.
20
In
this
definition
of
A,
the
constant
e is
assumed
to be
equal
to
exp(I)
=
2.718281828....
429

430
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
Such
a
variation
of the
porosity induces
a
variation
of
p(x.^(a))
as a
function
of
the
depth
d —
(z
u
—
xfn(a))
where
z
u
represents
the
z-coordinate
21
of the
horizontal unfolding plane
14:
For
the
sake
of
simplicity,
po
is
assumed
to be a
constant independent
of a:
this hypothesis allows
po to be
eliminated
from
the
final
equation (8.93),
and
its
actual
value
can
thus
be
ignored. According
to
equation (8.72),
it can be
observed
that,
at
geological time
t = 1, the
derivative
dx.LJdt
can be
roughly
approximated
by
Denning
p'(x[
t
](a)) as
and
taking into account
the
fact
that
the
geological time step
At
is
equal
to
(-1)
between
the
states
x^a)
and
X[
0
](a),
it can be
deduced
from
(8.88)
and
(8.89)
that
The
continuity equation (8.85)
at
geological time
t —
I
can
then
be
rewritten
as follows:
It can be
observed
that
Consequently,
from
equations (8.89),
(8.90),
and
(8.91),
at
geological time
t = 1, the
continuity equation (8.85)
can be
approximated
by
Finally, introducing
the
function
p,(x.^(a))
defined
by
it
can be
concluded
that
the
continuity equation (8.85)
is
approximately equiv-
alent
to
21
It is
assumed
that
the z
axis
is
oriented
positively
upward.

8.6.
UNFOLDING
A
STACK
OF
LAYERS
Definin g
Coni(r,
//|a,
C)
Using
notations introduced
in
section
(8.6.3),
for any
3-cell
C(oi),
the
value
D(r\a,C)
is
defined
as
follows
as a
function
of
derivatives
of r
computed
at
the
center
of C =
C(a):
In
other words,
D(r\a,C)
is
equal
to
four
times
the
approximation
of the
divergence
of r at the
center
of the
3-cell
C:
Prom
equations (8.81),
(8.82),
and
(8.83)
we
deduce
that
Let
fj,(a,C}
be the
value
of the
function
//,
denned
by
equation
(8.92)
at the
center
of the
3-cell
C(a).
By
definition,
the
function
Cont(r,
JJL
a,
C}
is
defined
as
follows
for any
3-cell
C(a)
of the
grid:
Taking into account equation (8.95) clearly shows
that
Cont(r,(j,\a,C)
is ap-
proximately equal
to
four
times
the
left-hand side
of the
equation
of
continuity
(8.93).
As a
consequence,
the
mass
of
terrains
will
be
preserved
if the
following
constraint
is
honored
for any
3-cell
C(a)
of the
grid:
This
constraint
is
linear relative
to
components
of the
restoration vectors
at
vertices
of the
3-cell
C(oi)
and can
thus
be
easily turned into
a
DSI
constraint:
this
is
precisely
the
goal
of the
next
section.
431

432
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
DSI
constraint
Let
d£,
dy,
d^
+
,
d
c
~,
and
a
c
be
coefficients
such
that
and let
{A
v
,
c
-,(j3}
:
(3 6
fJ}
be
associated
coefficients
denned
as
follows:
Note
that
the
square
of
coefficients
{A^
c
\(fi)}
so
denned
sum up to 1:
Using
these
coefficients,
it can be
checked
that
In
other words,
the
constraint
(8.98)
is
equivalent
to the
following
normalized
DSI
constraint:
The
index
K(C)
in the
above equation represents
the DSI
constraint associ-
ated with
the
3-cell
C(a)
where
the
continuity equation
is
evaluated.
Ac-
cording
to
equations
(4.49),
each
non-null
coefficient
{^(
c
\(/3)}
induces
a
series
of
three
pairs
of
terms
{^
(c)
(/?),f*
(c)
(/3|r)},
{^
(c)
(/3),f^
(c)
(/5|r)}
and
{^(
c
)(^)'f^(c)(^l
r
)}
occurring
in the
local
form
of the DSI
equation.
For
example,
the
terms related
to the
node
a of the
3-cell
C(a)
take
the
following
form:
Theoretically,
terms associated with other non-null
coefficients
{A^,,(@)}
should also
be
denned
in a
similar way. However,
from
a
practical point
of

8.6.
UNFOLDING
A
STACK
OF
LAYERS
view,
this
is not at all
necessary:
it can be
verified
that
the
same result
can be
obtained
by
replacing
all
these terms
by the following
terms
{7^*
(/3},
F^*
(J3
r)}
deduced
from
those
defined
by the
equation (8.101)
and
where
K*
=
K*(£
xy
,
a)
represents
a
composite
DSI
constraint:
8.6.5
Minimum-Deformation
constraint
According
to the
Minimum-Deformation principle introduced
in
section (8.4.11),
the field of
restoration vectors r(x) must minimize
the
components
of the six
independent components
of the
strain tensor
8:
For the
sake
of
simplicity, notations introduced
in
section (8.6.3)
are
used,
and
it
is
convenient
to
specify
that
the
above equation should
be
honored only
at
the
center
of any
3-cell
C(a)
of the
regular rectilinear 3-grid
not cut by a
fault.
According
to
equation (8.57)
and
constraints (8.103),
it is
equivalent
to say
that,
for any
3-cell
C*(a),
we
should have
In
practice, second-order terms
in the
above constraints are, generally,
an
order
of
magnitude
lower
than
those
of first-order
terms.
As a
consequence,
these second-order terms
can be
neglected:
the
above equations reduce
to
the six
following
equations, which
are
linear relative
to
components
of the
restoration vector
r:
The
next sections show
how
these equations
can be
turned into
DSI
con-
straints.
Defining
£"
X
i
X
j
(r|a,
C)
According
to the
numerical technique introduced
in
section
(8.6.3),
it is
always
possible
to
evaluate derivatives
of the
restoration vector
r at the
center
of any
3-cell.
Let
-E^ox^
(r a, C) be the
function
defined
as
follows
at the
center
of a
3-cell
C(a):
433
434
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
According
to
equation (8.104),
it is
clear
that
E-^i-^j
and
^x*xj
evaluated
at
the
center
of
C(oi)
are
linked
by the
following
relationship:
Using
approximations (8.81), (8.82),
and
(8.83),
it is
easy
to
evaluate
these
values
E^i^j.
For
simplicity's sake
and
according
to
notations (8.79),
in the
following,
the
components
(x^x^x
3
)
and
(r^r^r
3
)
of the
vectors
x and r
will
be
noted
(x, y,
z)
and
(r
x
,
r
y
,
r
z
),
respectively,
so
that,
for any
3-cell
C(a)
we
can
write
The
other terms
E
xz
,
E
yz
,
E
xx
,
E
yy
,
and
E
zz
can be
defined
in a
similar
way:

8.6.
UNFOLDING
A
STACK
OF
LAYERS
DSI
constraints
As
a
tutorial example,
let us
address
the
problem
of
building
a DSI
constraint
to
minimize
the
component
i^x
2
=
£
xy
of the
strain tensor. According
to
equation (8.105),
at the
center
of the
cell
C(ot),
this
is
equivalent
to the
following
constraint:
Let
d^,^.
d!f,/
.
and
cr£,,
be
coefficients
such
that
•^
I
^
y
y/'Ly
y
and let
{A^
c
J/3)
:
(3 €
£)}
be
associated
coefficients
defined
as
follows:
Note
that
the
square
of
coefficients
{A^,
C
J(3}}
so
defined
sum to 1:
Using
these
coefficients,
it can be
verified
that
In
other words,
the
constraint
(8.112)
is
equivalent
to the
following
normalized
DSI
constraint:
It
should
be
noted
that
the
index
«(C
f
)
in
equation (8.114) represents
the DSI
constraint
and
depends
on the
3-cell
C =
C(a)
where
the
component
£
xy
of
the
strain tensor
is
estimated. According
to
equations
(4.49),
to
each non-null
435

436
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
coefficient
{A
v
,-,(f3}}
corresponds
two
pairs
of
terms
(7^(
c
)(/3),
r^/^(/3|r)}
and
i^«Cc)(^)'
«(c)(^l
r
)}
that
occur
i
n
the
local
form
of the
DSI
equation.
For
example,
terms related
to the
node
a of the
3-cell
C(a)
take
the
following
form:
The
terms associated with other non-null
coefficients
{A
v
,^(f3}}
should also
be
denned
in a
similar
way.
However,
from
a
practical point
of
view,
this
is
not at all
necessary:
the
same result
can be
obtained
by
replacing
all
these
terms
by the
terms
{7^(/?),r^(/3|r)}
and
{7^(/3),r^(/?|r)}
deduced
from
those
defined
by
equation (8.115)
and
where
K*
=
K*(£
xy
,a}
represents
a
composite
DSI
constraint:
The
minimization
of the
other independent components
£
xz
,
£
yz
,
£
xx
,
£
yy
,
and
£
zz
of the
strain tensor
£ can be
achieved
in a
similar
way.
Comment
A
slight,
but
important,
difference
should
be
noted between pairs
of
terms
{7^*,
r^*}
defined
by
equation
(8.102)
and
those
defined
by
equations (8.116):
• In the
case
of the
Mass-Preservation constraint,
the sum is
performed
on the
whole
set
Tl(a)
of
cells surrounding
the
node
a
even
in the
neighborhood
of
faults.
This
is
necessary
to
avoid gaps
and
overlaps, which could occur
between
fault blocks along
the
faults.
• In the
case
of the
Minimum-Deformation constraint,
the sum is
restricted
to the set
72/
(a) of
cells surrounding
the
node
a and not cut but a
fault.
Such
a
restriction
is
necessary
to
allow large deformations
to
occur
in the
neighborhood
of
faults.
8.6.6
Other possible
DSI
constraints
As
usual with
DSI,
the
more constraints there
are,
the
more
the
solution
gen-
erated
by DSI has a
chance
of
being "geologically" admissible. Potentially
there
is
nothing
to
limit
the
choice
of
such additional constraints except
com-
mon
sense.
In
this section,
as an
example,
we
present
a few
such additional
constraints, which
can be
used
in
combination with
the
Mass-Preservation
and the
Structural constraints presented
in the
previous sections.

8.6.
UNFOLDING
A
STACK
OF
LAYERS
Pin-Poin t
constraint
The
simplest additional
soft
constraint
that
one can
think
of
introducing
is to
specify
that
a
given point
x(a)
called "Pin-Point"
has to
keep
one (or
several)
of
its
coordinates
{x
t/
(a)
: v
—
x,
y or z} fixed
during
the
restoration
process.
Such
a
constraint
is
equivalent
to
installing
a
fuzzy
Control-Point constraint
(see section
(4.7))
specifying
that
the
corresponding component
r
I/
(a)
of the
restoration vector
at
location
x(a)
is
equal
to
zero.
Note
that
the
notion
of
"Pin-Line" introduced
by
Dahlstrom [53]
can be
modeled
as
series
of
Pin-Points.
Tangent-to-Fault
constraint
Consider
a
node
a €
il
located
in the
neighborhood
of a
fault
T
and
charac-
terized
by the
fact
that
an
edge
(a,
(3)
incident
to a is cut by
F.
Let
Njr(a)
be
the
average normal
to
F
in the
neighborhood
of a. In the
case where
the
restoration vector
r(o;)
is
small,
it is
sometimes possible
to
assume
that
this
vector must
be
approximately tangent
to
T\
this
is
equivalent
to
saying
that
the
following
constraint
c =
c(a,
J-}
should
be
honored:
Assuming
that
N^(a)
is a
unit vector,
it can be
observed
that
such
a
con-
straint
can be
turned into
the
following
normalized
DSI
constraint:
where
the
coefficients
{A^((3)}
and
b
c
are
defined
by
According
to
equations
(4.49),
it can be
concluded
that
the
associated
terms
7^
(a) and
F^(a|r)
occurring
in the
local
form
of the DSI
equation
are
such
that
In
the
case where
the
fault-throw direction
t(a)
at
node
a is
known (see
page 372),
in
equations (8.117)
and
(8.118)
it may be
wise
to
replace
the
unit
normal vector
N^a)
by the
vector
N^-(a)
defined
as
follows:
437
