Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


408
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
is
thus
a
unit tensor:
From this
paleo-geographic
coordinates paradigm,
it can be
concluded
that
the
problem
of
unfolding/unfaulting
a
horizon
H
=
H[^
comes down
to the
search
for
a
particular parameterization
u(x)
of H
where
the
parametric domain
D
is
identified with
the
unfolded/unfaulted version
H^
of
H:
In
practice,
the
discrete model
M
2
(Q,
N,
u,C
u
)
is
used
for
computing this
parameterization
at the
nodes
of the
triangulated surface
T(H).
For
this
purpose,
it is
necessary
to add two
sets
of
DSI
constraints
to
Cu'-
• A first set of
constraints
has to be
installed
to
preserve
the
continuity
of the
components
w
1
and
w
2
of u
across
the
fault
traces. These
constraints
corre-
spond
to the
C°
and
C
l
pseudo-continuity
constraints
presented
in
sections
(6.4.2)
and
(6.4.3).
• A
second
set of
constraints
must
also
be
installed
to
define
the
type
of
unfold-
ing
mechanism.
These
constraints
will
be
presented
in the
following
sections.
It
should
be
noted
that
to
install
the
C°
and
C
l
pseudo-continuity
constraints
mentioned above requires choosing
a
point-to-point association between each
pair
of
twin
fault
traces (see section
(6.3.1)).
The
resulting parameterization
u is
strongly dependent
on
these associations,
and
special care must
be
taken
to
avoid introducing irrelevant distortions.
In
practice,
one or
several
of the
following
approaches
can be
used
to
build such associations:
• The
computed
fault-throw
directions
and
fault
striae
defined
on
pages
373
and 375 can be
used
to
identify
twin
pairs
of
points.
• An
automatic
algorithm
based
on the
geometry
and
topology
of the
fault
traces
can
also
be
used
to
identify
pairs
of
points.
•
Finally,
an
interactive
approach
can be
used
for
editing
the
automatic
associ-
ations
generated
by the two
approaches
first
proposed.
One
may
also choose
not to
link twin fault traces with
C°
and
C
l
pseudo-
continuity
constraints.
In
such
a
case,
gaps
and
overlaps
may
appear
in the
unfolded
state
of
these fault traces, which
can be
interpreted
as
inconsistencies
in
the
geometry
of the
associated
fault
in the
current
folded
state.
Isometric-mapping-based
method
Except where there
is a
specific
genetic reason (see comment
on
page
411),
it
makes sense
to
assume
that
the
horizon
H
=
H^
to be
unfolded/unfaulted
should preserve
its
metric properties (areas, angles,
and
lengths)
as far as
possible throughout geological time. Taking into account
the
fact
that
H^
was
assumed
to be a
part
of the
unfolding plane
U,
this implies
that
H
=
H^
must
be
isometric
to a
plane.
In
other words,
the
parameterization u(x)
of

8.5.
UNFOLDING
A
HORIZON
409
Figure
8.17
One
more
example
of
unfolding/unfaulting
of
a
triangulated
surface
based
on a
global
parameterization
using
isometric
DSI
constraints:
the
surface
area
is
preserved
with
a
relative
precision
of
10~
3
.
The
isoparametric
curves
are
represented
by
thin
lines
in the
exploded
view
(EAEG-overthrust
model
[6]).
H
corresponding
to the
above
paleo-geographic
coordinates paradigm must
generate
for H a
metric tensor
G,
approximately equal
to the
unit tensor:
This
is
typically
an
isometric constraint
for the
parameterization
u.
It has
been shown
in
section
(6.5.2)
how
such
a
constraint
can be
honored when
u is
interpolated
on the
triangulated
surface
T(H}
with
the DSI
algorithm based
on the
discrete model
.M
2
(f2,
TV,
u,C
u
)-
In
practice,
the
technique presented
in
section (6.5)
is
particularly
well
adapted
to the
unfolding
problem, and,
as
shown
in figures
(8.16)
and
(8.17), yields excellent results.
Figures (8.17)
and
(8.18) show
that
the
unfolding/unfaulting method
so
defined
is
applicable even
in
cases where
the
initial
surface
cannot
be
projected
simply
onto
a
horizontal plane,
that
is,
without overlaps
and/or
gaps.
Projection
based
method
Let
{-ftJ!]
:
i
=
1,
• •
-,
m}
be a
partition
of H
=
H^
into
a
series
of
m
polygonal
patches;
for
example,
• as
suggested
by
Rouby
et
al.
[187],
each
patch
Hl^
may
consist
of a
subset
of
triangles
of
T(H]
corresponding
to a
fault
block;
• as
suggested
by
Gratier
et al.
[95],
each
patch
Hfa
may be
reduced
to a
single
triangle
ofT(H).
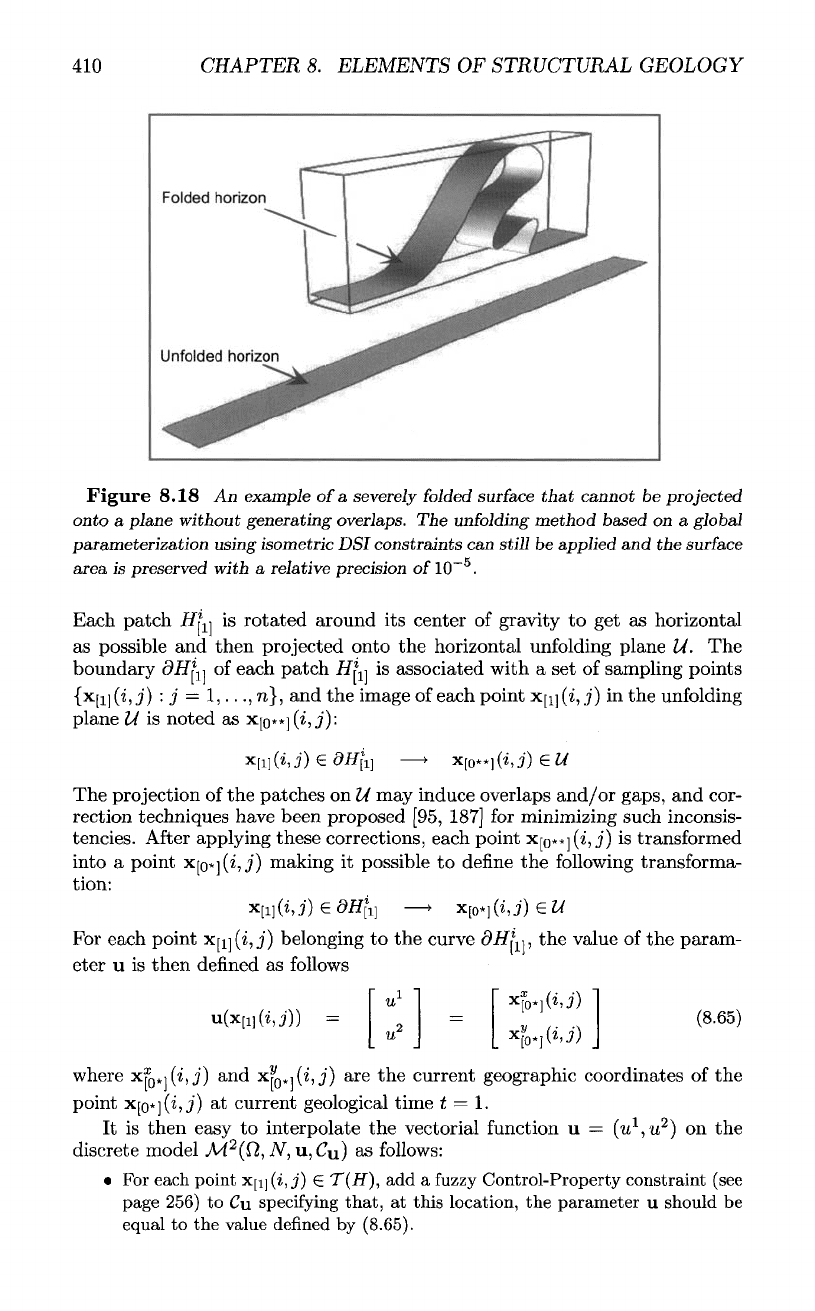
410
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
Figure
8.18
An
example
of
a
severely
folded
surface
that
cannot
be
projected
onto
a
plane
without
generating overlaps.
The
unfolding
method
based
on a
global
parameterization using isometric
DSI
constraints
can
still
be
applied
and the
surface
area
is
preserved
with
a
relative precision
of
10~
5
.
Each patch
HI,
is
rotated around
its
center
of
gravity
to get as
horizontal
as
possible
and
then projected onto
the
horizontal
unfolding
plane
U.
The
boundary
dH^
of
each patch
HI-,
is
associated with
a set of
sampling points
{x^
(i,j)
:
j =
1,...,
n},
and the
image
of
each point
X[i]
(i,
j) in the
unfolding
plane
U
is
noted
as
X[o**](i,jf):
The
projection
of the
patches
on U may
induce overlaps and/or gaps,
and
cor-
rection techniques have been proposed [95, 187]
for
minimizing such inconsis-
tencies.
After
applying these corrections, each point
X[
0
**](i,
j)
is
transformed
into
a
point
X[
0
*](«,j)
making
it
possible
to
define
the
following
transforma-
tion:
For
each point
X[i](i,
j}
belonging
to the
curve
dHfa,
the
value
of the
param-
eter
u is
then
defined
as
follows
where
x?
Qi
,,(i,j)
and
x¥
Qi
,,(i,j)
are the
current geographic coordinates
of the
point
X[o*](i,j)
at
current geological time
t = 1.
It is
then easy
to
interpolate
the
vectorial
function
u =
(u
l
,u
2
)
on the
discrete model
M
2
(fl,
N, u,
C
u
)
as
follows:
• For
each point
X[i](i,j)
€
T(H),
add a
fuzzy
Control-Property constraint (see
page
256)
to
Cu
specifying
that,
at
this
location,
the
parameter
u
should
be
equal
to the
value
denned
by
(8.65).

8.5.
UNFOLDING
A
HORIZON
411
• For
each
triangle
T
e
T(H),
add a
Constant-Gradient
constraint
(see
page
261)
to
Cu
specifying
that
u
should
have,
approximately,
a
constant
gradient
on
T and its
adjacent
triangles.
•
RunDSIon
M
2
(17,]V,u,Cu).
The
parameter
u can
then
be
linearly interpolated
on
each triangle
T, as
indicated
in
section
(6.1.3).
Unfolding
Let
us
assume
that
a
parameterization u(x)
of H
=
H[^
has
been obtained
by
any one of the
methods presented above.
The flat
surface
#[o*]
embedded
in
the 3D
space
and
defined
by
appears
as an
unfolded/unfaulted version
of H
located
in the
horizontal plane
ZY
at the
given altitude
z =
z
u
.
In
practice,
as
shown
in figure
(8.20),
the
sur-
face
#[o*]
must
be
translated
and
rotated
in the
unfolding plane
U to
become
coincident with
the
presumed location
of the
initial
unfolded/unfaulted ver-
sion
_ff[
0
]
of H.
Section
(8.5.2)
shows
how to
determine such
a
displacement
in
an
optimal way.
Comment:
The
case
of
listric
faults
A
"listric fault"
or
"syndepositional
fault"
is a
particular case
of
faults where
one
of the two
associated
fault
blocks continued
to
move during
the
deposi-
tional
time lag.
For
example,
in the
cross section represented
in figure
(8.19),
the
sediments
are
assumed
to
come
from
the
left-hand side
of the
listric fault,
and the two
fault
blocks behave
as
follows:
• Few
sediments
are
assumed
to be
deposited
on the
right-hand
side
of the
fault,
and
they
deposit
according
to
horizontal
layers
with
a
constant
thickness;
for
this
reason,
we
propose
calling
this
fault
block
the
"neutral
fault
block."
• On the
contrary,
the
opposite
fault
block
(the
right
one in figure
(8.19))
is
sliding
downward
during
the
sedimentation process
and the
sediments
are
filling the gap
with
a
vertical
speed
that
is a
decreasing
function
of the
distance
to the
fault;
for
this
reason,
we
propose
calling
this
fault
block
the
"active
fault
block."
Due
to the
so-called "roll-over" geological mechanism [235, 213],
in the
active
fault
block
it can be
observed
that
• the
layers
have
a
thickness
that
is a
decreasing
function
of the
distance
to the
fault;
• the
area
of the
horizons
is
reduced
throughout
geological
time
by a
factor
that
is
a
decreasing
function
of the
distance
to the
fault;

412
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
Figure
8.19
Vertical
cross
section showing
the two
steps
of
the 2D
simple-shear
mechanism
in the
case
of
a
listric
fault:
the top
horizon
is
projected onto
U
according
to a
given direction
of
shearing
s and
then translated
to
remove gaps.
• far
away
from the
fault,
the
active fault block tends
to
have
a
behavior similar
to the one of the
neutral
fault
block,
and the
horizons tend
to
have
a
constant
area throughout geological time.
In
such
a
case
and as
illustrated
in figure
(8.19),
the
unfolding
mechanism,
called
"simple-shear"
is
well defined
in a 2D
cross
section
of a
vertical
plane
Xi
and can be
split
into
the
following
two
steps:
1.
Choose
a
given
shearing
direction
16
s
and,
for
each
point
X[i](i,j)
be-
longing
to the
intersection
H\^(Xi)
of
H^
with
the
cross
section
Xi,
proceed
as
follows:
•
draw
the
straight
line
A(x[i](«,_;'),s)
passing through
X[i](i,j)
and
par-
allel
to s;
•
define
the
image
X[
0
**](i,
j) as the
intersection
of
A(x[i](i,
<
7'),
s)
with
the
unfolding
plane
U.
2.
Translate
globally
the set of
points
{x[o**](i,
j)
:
j =
1,...,
n}
by a
vector
ti
chosen
to
minimize
gaps
and
overlaps,
and
define
the set
{x[
0
*](i,
j)}
16
This
direction, which depends
on
geomechanical characteristics
of the
terrains,
can be
chosen
freely
or it can be
determined numerically using
an
optimization method such
as
the one
proposed
by
Kerr
et
al.
[122].

8.5. UNFOLDING
A
HORIZON
413
as
follows:
It is
clear
that,
according
to
this
unfolding
mechanism,
in the
active
fault
block
the
area
of the
horizon
H
=
H^
to be
unfolded differs
locally
from
the
area
of
#[o]-
However,
it can be
observed
that,
even
in
such
a
case,
when
far
away
from
the
listric
faults,
the
metric
properties
of the
horizon
H are
still
preserved
in the
active
fault
block.
At
this
point,
it is
useful
to
recall
the
respective
roles
of the
three
isometric
constraints
(6.80):
• the two first
isometric constraints
(6.80)-1
and
(6.80)-2
are
used
to
preserve
the
area
of H and the
lenght
of
segments drawn
on H
during
the
restoration
process;
• the
third isometric constraint
(6.80)-3
is
used
to
preserve
the
angles drawn
on
H
during
the
restoration process.
Consequently,
this
suggests
that
we
continue
to use the
method
based
on
isometric-mapping,
with
the
following modifications
whose
purpose
is to
allow
the
area
of the
horizon
H to
vary
in the
active
fault
block:
• at
each node
a of the
horizon
H to be
unfolded,
define
a
function
A(a)
taking
its
values
in the
range
[0,1]
and
measuring
the
aptitude
of the
area
of H to
vary locally throughout geological time;
•
choose
a
"basic" certainty factor
WQ
used
for
weighting
the
isometric con-
straints (6.80);
• use the
certainty factor
073(0:)
defined
as
follows
to
weight
the
isometric con-
straint
(6.80)-3
at
node
a:
• use the
certainty factor
w\,i(a]
defined
as
follows
to
weight
the
isometric
constraints
(6.80)-1
and
(6.80)-2
at
node
a:
Proceeding
that
way
allows
the
distortions
to be
minimized
everywhere
while
taking
into
account
the
fact
that
the
area
of the
unfolded
horizon
may not be
constant
close
to the
listric
fault
in the
active
fault
block.
A
propos
of the
Minimum-Deformation
principle
According
to
equations
(8.62)
and
(8.64),
the
horizon unfolding
method
based
on the
isometric-mapping
technique
presented
on
page
408
takes
into
account
the two following
constraints
explicitly:
• The
metric tensor
G[
0
]
of the
unfolded
horizon
H^
is
strictly equal
to the
unit
tensor:
• The
metric tensor
G of the
folded
horizon
H is as
close
as
possible
to the
unit
tensor:
414
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
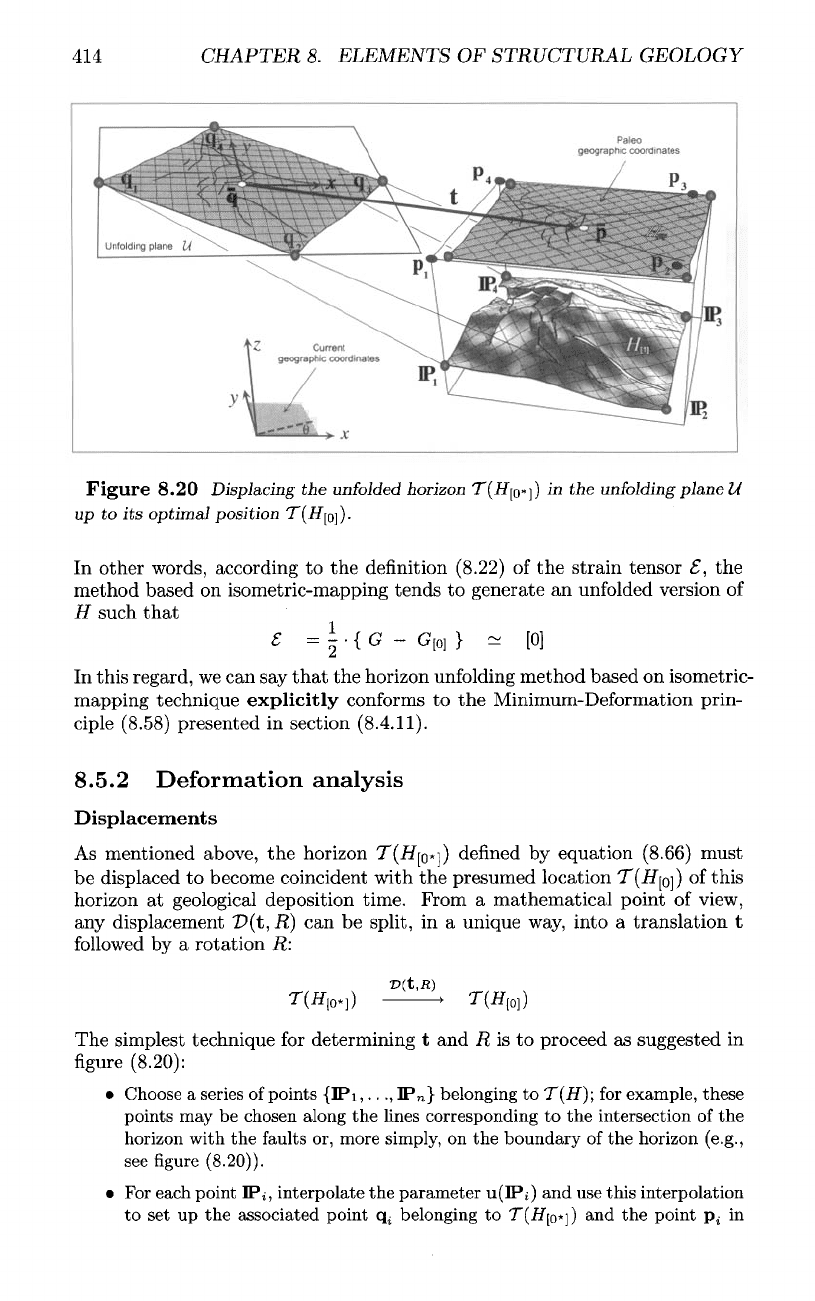
Figure
8.20
Displacing
the
unfolded
horizon
T(H[
0
*])
in the
unfolding
plane
U
up
to its
optimal
position
T(H^}.
In
other words, according
to the
definition
(8.22)
of the
strain tensor
£,
the
method based
on
isometric-mapping tends
to
generate
an
unfolded
version
of
H
such
that
In
this regard,
we can say
that
the
horizon
unfolding
method based
on
isometric-
mapping
technique
explicitly
conforms
to the
Minimum-Deformation prin-
ciple
(8.58) presented
in
section (8.4.11).
8.5.2
Deformation analysis
Displacements
As
mentioned above,
the
horizon
T(#[
0
*])
defined
by
equation
(8.66)
must
be
displaced
to
become coincident with
the
presumed location
T(H^)
of
this
horizon
at
geological deposition time. From
a
mathematical point
of
view,
any
displacement
T>(t,R)
can be
split,
in a
unique way, into
a
translation
t
followed
by a
rotation
R:
The
simplest technique
for
determining
t and R is to
proceed
as
suggested
in
figure (8.20):
•
Choose
a
series
of
points
{IPi,...,
IP
n
}
belonging
to
T(H);
for
example,
these
points
may be
chosen
along
the
lines
corresponding
to the
intersection
of the
horizon
with
the
faults
or,
more
simply,
on the
boundary
of the
horizon
(e.g.,
see figure
(8.20)).
• For
each
point
IPi,
interpolate
the
parameter
u(lPi)
and use
this
interpolation
to set up the
associated
point
q^
belonging
to
T(H[
0
*])
and the
point
PJ
in

8.5. UNFOLDING
A
HORIZON
415
the
plane
z —
z
u
,
as
defined
by
Note
that
p
i
is no
more than
the
vertical projection
of
D?i
onto
the
unfolding
plane
Li.
•
Determine
t and R to
minimize
the
following
criterion
J~(t,
7?),
where
£>(t,
R)o
QJ
represents
the
image
of
q^
by the
displacement
T>(t,
R):
As
an
exercise,
it is
verifiable
that
the
translation
t and the
rotation
R
min-
imizing
the
criterion
J(t,
R}
defined
by the
above
equation
(8.67)
can be
determined
as
follows:
• The
translation vector
t is
such
that
where
p
represents
the
center
of
gravity
of the
points
{p
1;
..
,,p
n
},
while
q
represents
the
center
of
gravity
of the
points
{q
1
,...,
q
n
}.
• The
center
of the
rotation
R is
coincident with
p and the
angle
9 of the
rotation
in the
unfolding
plane
ti
is
such
that
where
A and B are
defined
by
The
integer
k in
equation
(8.68)
is
assumed
to be
either equal
to 0 or 1 and
these
two
values correspond
to the
maximum
and the
minimum
of
J~(t,R),
respectively;
in
practice, only
the
value corresponding
to the
minimum
of
^7(t,
R)
must
be
retained.
The
restoration
vector
r(x)
is
then
defined
at any
location
x on
T(H]
as
follows:
As
illustrated
in figure
(8.21),
the field of
restoration
vectors
so
defined
de-
pends
strongly
on the
"fixed"
region
defined
by the set of
points
(IPi,...,
TP
n
}
chosen
on
T(H)
and
clearly
shows
how the
surface
has
moved
relative
to
this
fixed region.
416
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
Figure
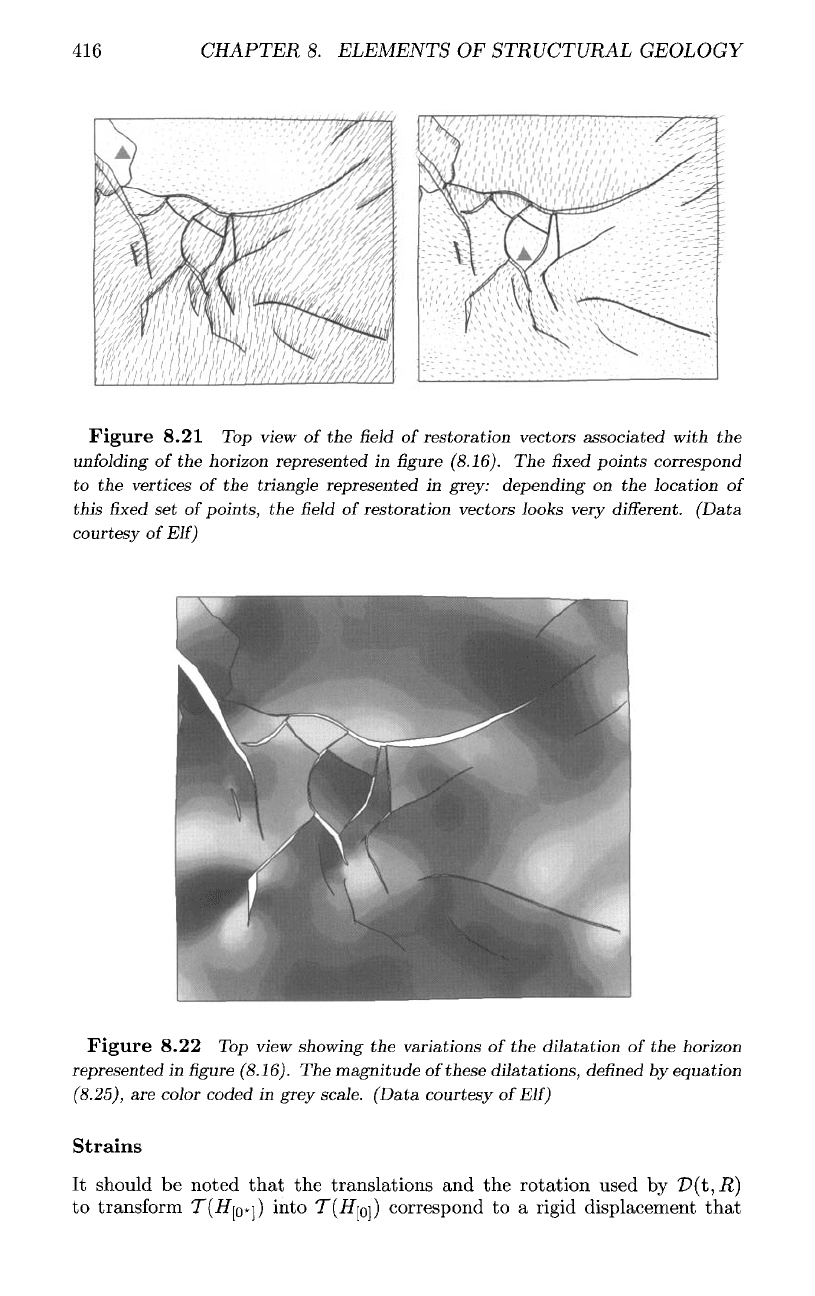
8.21
Top
view
of the field
of
restoration vectors associated
with
the
unfolding
of the
horizon represented
in figure
(8.16).
The fixed
points
correspond
to the
vertices
of the
triangle represented
in
grey: depending
on the
location
of
this
fixed set
of
points,
the field of
restoration vectors looks very
different.
(Data
courtesy
of
Elf)
Figure
8.22
Top
view
showing
the
variations
of the
dilatation
of the
horizon
represented
in figure
(8.16).
The
magnitude
of
these dilatations,
defined
by
equation
(8.25),
are
color coded
in
grey scale. (Data courtesy
of
Elf)
Strains
It
should
be
noted
that
the
translations
and the
rotation
used
by
P(t,J?)
to
transform
T(H^)
into
T(H^)
correspond
to a
rigid
displacement
that

8.5.
UNFOLDING
A
HORIZON
417
Figure
8.23
Top
view
showing
the
principal
strain
directions
of the
horizon
represented
in figure
(8.16)
and
defined
by
equation
(8.43).
The
length
contrasts
of
these
vectors
are
magnified
by an
arbitrary
factor
and
reflect
the
deformations
of
a
circle
stuck
on the
unfolded
horizon.
In a
better
color
coded
representation
the
directions
corresponding
to
positive
elongations
e^
should
be
represented
in red
while
the
others
should
be
represented
in
blue.
(Data
courtesy
of
Elf)
generates
no
deformation.
If
{x(o:o),x(a!i),x(a;2)}
represents
the
location
of
the
vertices
of the
current triangle
T of
T(H]
and if the
following
notations
are
used
then,
according
to
equations
(6.25)
and
(6.30),
the
metric tensor
GT
associ-
ated
with
the
global parameterization
u(-)
on T is
such
that
According
to the
definition
(8.22)
and
from
equations
(8.62)
and
(8.69),
it is
easy
to
estimate
the
strain tensor
£ on
each triangle
T G
T(H\
as
follows:
According
to
equations
(8.26)
and
(8.35),
the
above estimation
of £
makes
it
possible
to
compute
the
dilatation
coefficient
9 and the
principal strain
directions
(W^)}
for
each triangle
T G
T(H}.
It is
interesting
to
observe
the
following:
